基于模拟评分的服装推荐改进算法

江学为， 田润雨， 卢方骁， 张 艺

(1. 武汉纺织大学 服装学院， 湖北 武汉 430073； 2. 武汉纺织大学 武汉纺织服装数字化工程技术研究中心， 湖北 武汉 430073； 3. 武汉大学 测绘学院， 湖北 武汉 430079)

近年来，随着大数据与智能技术的不断创新，电子商务进入高质量发展阶段[1-2]。服装精准营销成为服装企业关注的热点。服装推荐系统能够根据消费者喜好，提出符合消费者购买需求的建议，对精准营销有着重要意义[3-4]。传统服装推荐算法可分为2类：第1类是基于消费者群体划分的推荐算法，如基于消费者群体的协同过滤算法[5]；第2类是基于服装相似度的推荐算法, 如基于关键点服装款式识别的智能服装推荐系统[6]。第1类推荐算法利用不同方法对消费者进行相似性分析，将其划分为不同群体，根据同一群体对服装的喜好，判断该群体中消费者对某款服装的喜好。这类服装推荐系统不依赖消费者的历史消费数据，但对于新上市的服装，由于缺乏消费者评价，不能进行较为准确的推荐。第2类推荐算法对同一消费者的服装消费行为进行分析，通过将服装与历史消费数据进行相似性比较，推荐与曾购买过的服装相似的服装。这类算法适用于新款服装的推荐，但对于缺乏消费历史记录的消费者无法进行有效推荐[7]。

针对传统服装推荐算法存在的问题，有学者考虑到服装不同属性对消费者喜好的影响权重不同，对上述推荐算法进行改进，提出了基于层次分析法(AHP) 的服装推荐方法[8]。为进一步提高推荐算法准确度，尹定乾等[9]利用奇异值分解和相关系数对上述2类算法进行结合，提出了基于奇异值分解(SVD++) 改进的服装推荐算法，在一定程度上提高了推荐算法的准确性。但是，由于服装具有周期短、款式多、批量小，消费者对服装偏好会随着时间推移发生变化等特点[10]，需要进一步考虑消费者兴趣、消费者群体及历史消费数据对推荐准确性的影响。基于以上原因，本文考虑了服装属性与类别对消费者兴趣的影响，对服装的相关数据进行编码，并通过服装属性与消费者时序行为引入兴趣衰减函数，构建模拟评分模型，结合消费者群体进行卷积神经网络训练，建立了基于模拟评分服装推荐系统，以期进一步优化服装推荐算法。

1 模拟评分方法

本文针对服装属性和消费者时序行为对推荐算法进行改进，提出了基于模拟评分算法的服装推荐系统。模拟评分算法通过收集消费者的相关数据(服装的商品名和购买、浏览、收藏服装的时间)进行编码，并通过兴趣函数计算消费者对服装的偏好评分，然后将评分进行归一化和模糊化处理，最后使用卷积神经网络训练数据，建立服装推荐系统。

1.1 数据收集

本文试验对象为在校大学生，获得试验对象许可后，搜集其网络中与服装相关的信息：服装名称、购买时间、浏览时间、收藏时间、价格等数据。共收集了20位消费者的与服装相关的数据1 166条。由于消费者对服装的兴趣变化受到服装种类与购买时间、浏览时间、收藏时间的影响显著[11-12]，因此，使用服装的商品名称和购买记录、浏览记录、收藏服装的时间作为编码参数。由于价格等数据不能表达服装特性，所以对消费者兴趣不造成显著影响[13]，其不作为编码参数。

1.2 服装编码

图1示出词库编码示意图。

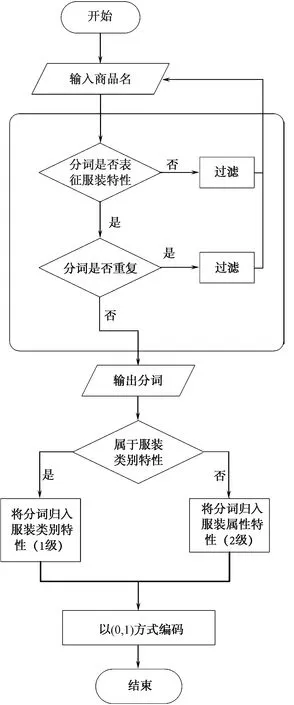
图1 词库编码示意图Fig.1 Schematic diagram of thesaurus coding

为提高数据分析的可靠性与模拟评分的准确性，首先对所收集数据进行预处理。预处理过程如下：根据分词的权重，利用分词算法对服装标签进行提取，并进行降序排列。选取前若干个分词，判断其是否能描述服装特性，是否与已有特性重复。若该分词不能描述服装特性或与已有特性重复则删除，重复该流程，直到提取的所有分词都可表征服装的特点。标签提取完成后，根据服装类别特点对标签进行一级编码，根据服装的属性特点进行二级编码。

以收集的3件T恤为例，其标签分别为：韩版、原宿、纯棉、宽松、T恤、短袖、露肩、上衣；韩版、简约、圆领、套头、修身、露肚脐、短袖、T恤；宽松、T恤、原宿、韩版、百搭、上衣、慵懒风。首先对标签进行去重处理并排序，根据服装类别可获得3个一级标签：T恤、上衣、短袖。根据服装属性可获得12个二级标签：韩版、原宿、宽松、纯棉、露肩、简约、圆领、套头、修身、露肚脐、百搭和慵懒风。当服装属性与标签匹配时，该项编码为1，否则为0，3件T恤编码如表1所示。

表1 服装编码表Tab.1 Clothing coding table

根据以上计算流程，对所有服装产品进行预处理，生成对应的编码数据库。

1.3 服装消费偏好

考虑时间对消费者兴趣的影响，本文根据艾宾浩斯记忆模型[14]，建立了基于欧氏距离的消费者服装兴趣衰减模型，并结合相似度评分修正模型构建了评分模拟算法，其计算过程如图2所示。以衬衫和T恤品类为例，计算服装消费偏好过程如下。

图2 模拟评分算法的计算过程Fig.2 Calculation process of simulation scoring algorithm

1)初始化消费者对服装的喜爱程度(评分)，将该消费者有记录的初始化服装评分设置为100分。

2)计算每件服装的时间间隔。由于消费者对服装的兴趣衰减程度并不以天为周期急剧下降，因此，为方便计算，将每一个兴趣衰减周期定义为30 d。 将实际购买、浏览和收藏服装的时间除以30 d， 计算时间间隔t(t属于无量纲单位)。有时间记录的数据可直接计算时间间隔；无时间记录的数据，利用反距离加权插值法进行加权进行计算[15]，公式如下:

式中：tc为无记录时间的服装时间间隔；i为有时间记录的服装编号；n为有时间记录的服装件数；c为待求时间间隔编号；ti为第i件有时间记录的服装的时间间隔；di为第i件有记录时间的服装向量与待求服装向量的欧氏距离。其中di的算法如下式所示：

式中：p为编码向量的维度；q为维度上限；xp,i为第i件已知时间间隔服装的p维编码；yp为待求时间间隔服装的p维编码。

3)基于兴趣衰减函数计算服装评分。艾宾浩斯记忆函数为M=79.975t-0.126[14]，该模型反映了记忆量M随时间t衰退的趋势。式中：0.126为衰减系数，79.975为常量。消费者的兴趣衰减过程类似于记忆衰退过程，随时间逐渐下降，因此，可采用记忆量与时间的关系分析兴趣衰减过程。但这二者的下降趋势并不完全相同，消费者在开始一段时间内保持对服装的兴趣不变。在兴趣与时间的关系式中，兴趣系数常量设为100。由于消费者对服装兴趣的衰减速度较慢[16]，所以本文利用范围为0.1～1.0的a系数对衰减速度进行调整，其函数为

M=100t-0.126a

为确定a的值，跟踪了3位消费者对1件服装在30、40、50、60、70、80、90 d的模拟评分，并比较了其均方误差如图3所示。当a= 0.6时，均方误差最小，因此，兴趣衰减公式表示为。

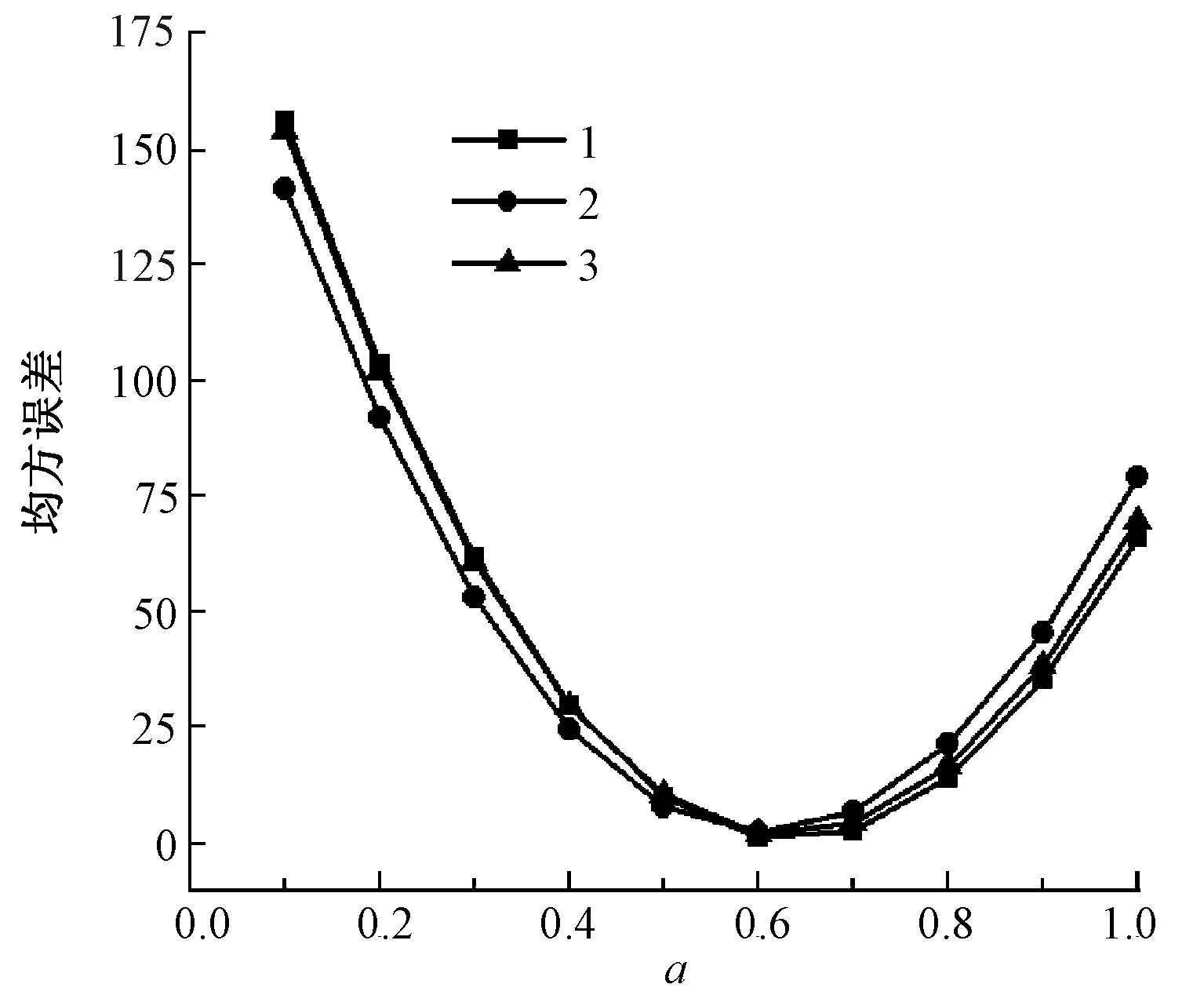
图3 a值对应的均方误差Fig.3 Mean square error for a

式中：mh为第h件服装的模拟评分；h为服装编号；th表示第h件服装的时间间隔。

4)获取消费者对当前服装的兴趣编码Yp。本文通过2种方式获取当前兴趣编码：若消费者当天曾购买服装，则此服装对应的编码为当前兴趣编码；若消费者当天未购买服装，则通过时间间隔倒数加权法[15]计算当前的兴趣编码，计算公式为

式中：Yp为当前兴趣的p维编码；p为编码向量的当前维度；l为服装件数；Xp,h为第h件服装的p维编码。

时间间隔倒数加权法是根据1组已知数据计算未知数据的插值方法。Xp,h代表了1组已知数据，即有时间记录服装的p维编码，Yp则是未知待求数据。上式中分子为已知服装编码除以时间间隔，用以计算服装单位编码，将所有服装的单位编码求和计算总体服装单位编码。总体服装单位编码包含了消费者有时间记录服装的编码特征，用以表征消费者对服装结构、风格和面料的兴趣。分母为已知服装的时间间隔的倒数，是为了将总体服装单位编码去单位化，即当前兴趣的p维编码Yp。

5)计算消费者当前兴趣编码与历史消费编码的欧氏距离。由于消费者对服装的兴趣具有一定主观性，可能会随着时间衰减，也可能会不变或升高，因此，在计算消费者对服装的喜好时，不能仅根据时间计算，还应该考虑当前服装编码与消费者历史兴趣编码之间的关系(欧式距离D)，其计算公式为

式中：Dh为第h件服装与当前兴趣编码间的欧氏距离；Q为维度上限。Dh表示2个编码向量间的多维空间距离，编码间距离越近，2个编码对应服装的相似度越高，则该服装的评分也应越高。

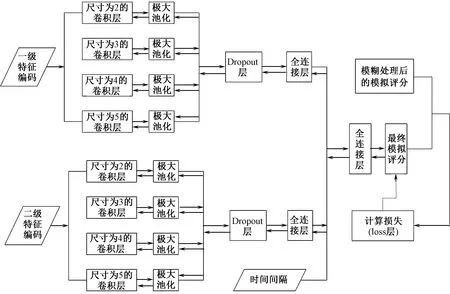
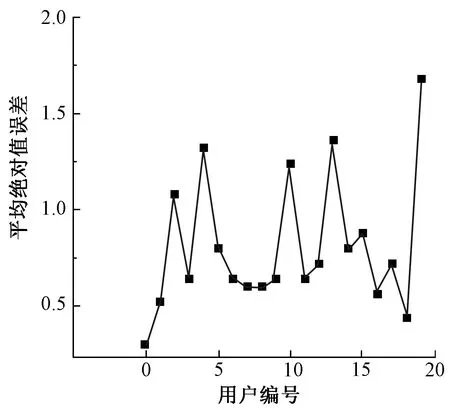
6)构建基于Dh与mh的模拟评分修正模型。为提高推荐系统的准确性，通过参数Dh对初始模拟评分进行修正。为保持计算的一致性，模型以选择e(1-Dh/Dmax)b为修正系数；b为调整系数，取值范围为0.1～1.0。当Dh越小时，消费者对当前服装的兴趣越高，模拟评分越高。当Dh=Dmax，e(1-Dh/Dmax)b=1时，表示不需要修正模拟评分mh，因此Mh=mh。而当Dh

Mh=e(1-Dh/Dmax)bmh

式中：Mh表示修正后的模拟评分；Dmax表示服装与消费者当前兴趣间欧氏距离的最大值。为保证更加接近真实值，分别计算了b取不同值时，修正后模拟评分与实际评分的均方误差如图4所示。结果表明，b=0.3时，均方误差最小，因此，模型表示为

图4 b值对应的均方误差Fig.4 Mean square error for b

Mh=e0.3(1-Dh/Dmax)mh

7)评分归一化和模糊化处理。为统一评分标准，将所有模拟评分归一化处理，计算公式为

式中：R为修正后的模拟评分；Rmax为修正后的最大模拟评分；Rnorm为归一化服装模拟评分。

为使模拟评分过程更接近真实情况，对时间与模拟评分进行了模糊化处理，并使用卷积神经网络进行训练，完成服装推荐。根据人的记忆特点将时间间隔分为5类(见表2)。通过将真实评分除以10，并利用四舍五入法取整进行评分模糊化处理。经过模糊化处理后，评分范围是0～10的整数。由于神经网络的输出在0～1之间，所以将已得到的评分除以10后进行训练。

表2 时间模糊化规则Tab.2 Time fuzzification rule

1.4 神经网络训练

神经网络训练过程是模拟人脑按照已得到的评分规则，对消费者的相关服装进行自动评分的过程，通过模糊处理的方式，使模拟评分更接近真实人脑的状态。将已经得到的143件服装的服装编码、时间间隔编码及模糊处理后的模拟评分作为训练的初始数据，经卷积层、池化层和全连接层处理，并通过loss层的反馈调节权重对模拟评分进一步修正。神经网络训练过程如图5所示[17]。

图5 文本卷积神经网络Fig.5 Text convolution neural network

2 模拟评分算法准确度评估

为验证模拟评分算法的准确性，本文根据20位消费者的消费特点，通过网络平台为每位消费者随机选择25件衬衫和T恤，然后分别通过模拟评分以及测评者评价的方式对500件服装进行评分。参照李克特五级评分法[18]，消费者按照五分制规则进行评分。定义为：1分为非常不满意，2分为不满意，3分为勉强满意，4分为满意，5分为非常满意。将模拟评分乘以100后，根据表3的转换规则，将模拟评分转化为五分制。

表3 评分转换规则Tab.3 Scoring conversion rules

为评价模拟评分的准确性，本文采用平均绝对值误差(MAE)作为评价指标[19]。指标MAE表示模拟评分和真实值评分之间绝对误差的平均值，计算公式如下：

式中：GAB表示通过模拟计算的消费者A对服装B的评分；G′AB表示消费者A对服装B的真实评分；N表示服装的总件数；U代表消费者测试集；I代表服装测试集。平均绝对值误差值越小，说明模拟评分与消费者评分误差越小，算法越准确。20位消费者对每件商品评分的平均绝对值误差值如图6所示。通过计算发现，20位消费者的平均绝对值误差值为0.808，其中70%消费者的平均绝对值误差小于0.8。

图6 消费者平均绝对值误差Fig.6 Mean absolute error value of users

奇异值分解算法(SVD)及SVD++算法被广泛应用于推荐系统与自然语言处理等领域，为提高预测准确性，尹定乾等[9]提出了基于SVD++的改进算法，并对服装推荐系统进行研究。该研究以2015年阿里巴巴移动推荐算法大赛的数据作为样本，分别利用SVD、SVD++和改进SVD++算法进行评分。通过比较三者评分的平均绝对值误差发现，改进SVD++算法最准确。通过与改进SVD++算法(0.832) 进行比较发现，本文模拟的平均绝对值误差降低了0.024，结果更准确。其中70%消费者的平均绝对值误差小于0.8，准确性有提升。

为进一步分析改进评分算法的效果，本文对评分平均绝对值误差大于1的消费者(占25%)进行分析。在本文调查中，消费者2、消费者4、消费者10、消费者13和消费者19的评分平均绝对值误差大于1，即平均每件商品的评分误差在1分以上。通过分析消费者4的训练集发现，该消费者的早期购物较多，缺少近期数据，难以捕捉消费者近期喜好，导致训练集中的数据评分普遍偏低，从而影响了评分。而消费者19在实验前后身份发生了变化，由大学生身份转变为上班族，其对服装的喜好由活泼风格变为沉稳风格，而这一变化无法被模拟评分算法捕捉，导致了较大误差。若不计以上影响，消费者的评分平均绝对值误差为0.632，相对于0.832大幅度降低，说明模拟评分算法的准确性有很大提高。

3 服装推荐与评测

由消费者评分规则及模拟评分转换规则可知，3分为消费者对服装偏好程度的临界点。评分大于3表示消费者在不同程度上喜欢被评测服装；评分小于3表示消费者在不同程度上不喜欢该服装。若某件服装模拟评分大于3，则系统将该服装推荐给消费者，否则不推荐。

为评价推荐结果的准确性，对消费者进行回访，分析消费者偏好是否与推荐一致。如果消费者偏好与推荐一致，则视为推荐准确，否则视为推荐错误。通过比较发现，55%消费者的推荐准确率为100%，35%消费者的推荐准确率为96%，5%消费者的推荐准确率为64%，5%消费者的推荐准确率为60%。导致推荐准确性较低的原因是消费者缺少一定时期的购买数据，或由于数据采样和回访期间身份转变导致的喜好变化。由以上分析可知，基于模拟评分的服装推荐系统对90%消费者的推荐准确率为96%及以上，仅有10%消费者的推荐准确率为60%～64%。

4 结 论

本文利用服装编码、时间间隔和欧氏距离等参数，建立了服装兴趣衰减函数，提出了模拟评分算法，并通过卷积神经网络建立了服装推荐系统。该算法结合了第1类和第2类传统推荐算法的优势，降低了推荐系统对历史消费数据的依赖。推荐系统通过兴趣编码间的欧式距离对模拟评分进行修正，降低了模拟评分与真实评分间的误差，从而提高了推荐的准确性。

在缺乏消费者一定时期内的服装消费数据及由外界引起消费喜好发生突然改变的情况下，基于模拟评分的服装推荐系统准确性会受到较大影响，因此，本文后期将针对这一问题，进一步优化算法，减少推荐系统对历史服装消费数据的依赖。