基于线性回归对比稳健估计的沉降监测数据分析

2022-01-05刘巍汪金花

华北理工大学学报(自然科学版) 2022年1期

刘巍，汪金花

(华北理工大学矿业工程学院，河北唐山 063210)

引言

楼房的变形监测对于人们的生活和生命安全有着重要的意义，沉降观测的数据起着决定作用。楼房沉降监测的观测分为3个时期：第一个时期为基坑开挖后要进行及时的观测；第二个时期为施工期间，在施工阶段观测的频率要大些，一般按3 d、5 d、7 d等确定周期；第3个时期为工程竣工后，竣工后的阶段观测频率可以相应减少，这主要是根据地基土类型以及地基沉降速度的快慢来决定，一般分为1个月，3个月或者半年不等。在沉降监测过程中，无论使用多么精密的仪器，总是无法避免人为因素和外界环境的影响所导致的粗差。当观测值中不含有粗差时，通常使用最小二乘法进行处理，线性拟合的效果较为准确；但在实际外业中，采集数据时会产生粗差，最小二乘法由于不具有抗差性而不能剔除粗差，有一定的局限性，而稳健估计则可以在数据含有粗差的时候进行抗差处理，进而减少粗差对观测值的影响，从而得到更好的拟合效果。国内部分学者对稳健估计处理沉降监测数据进行了研究，梁景辉[1]采用IGGIII稳健估计和最小二乘法分析大坝沉降数据，结果表明，使用IGGIII稳健估计法能够抗拒异常值干扰，提高数据精度。同时，稳健估计在其他领域应用也十分广泛。董元[2]等以水泥胶砂试块为实验对象，对它的光谱数据进行处理，分析水泥胶块质量大小与光谱反射率两者的线性关系，实验结果表明，在光谱数据含有噪声的情况下，稳健估计法拟合更加稳定。李卫强[3]在坐标拟合中进行GNSS坐标系的转换时，为避免粗差导致结果失真，引入了稳健估计模型从而提高了转换精度。上述研究结果表明，稳健估计在处理含有粗差的数据方面有着较多的应用，由此将稳健估计引入对房屋沉降监测数据的处理。

采用了线性模型和指数模型，在此基础上分别使用最小二乘和稳健估计2种方法对房屋沉降监测数据进行处理，通过对结果进行比较，得出2种方法的优缺点以及适用情况。

1 数据源

周口恒大时代新城位于周口东新区，占地面积为16.437 7 hm2，共有16栋楼，楼层高度在42～78 m之间，建筑面积为41.500 0 hm2。工程建设的任务是商住两用，小区所处的区域地貌整体平坦。该项目是对该小区的5#住宅楼进行沉降观测，基坑等级为一级。该楼的工程示意图如图1所示。

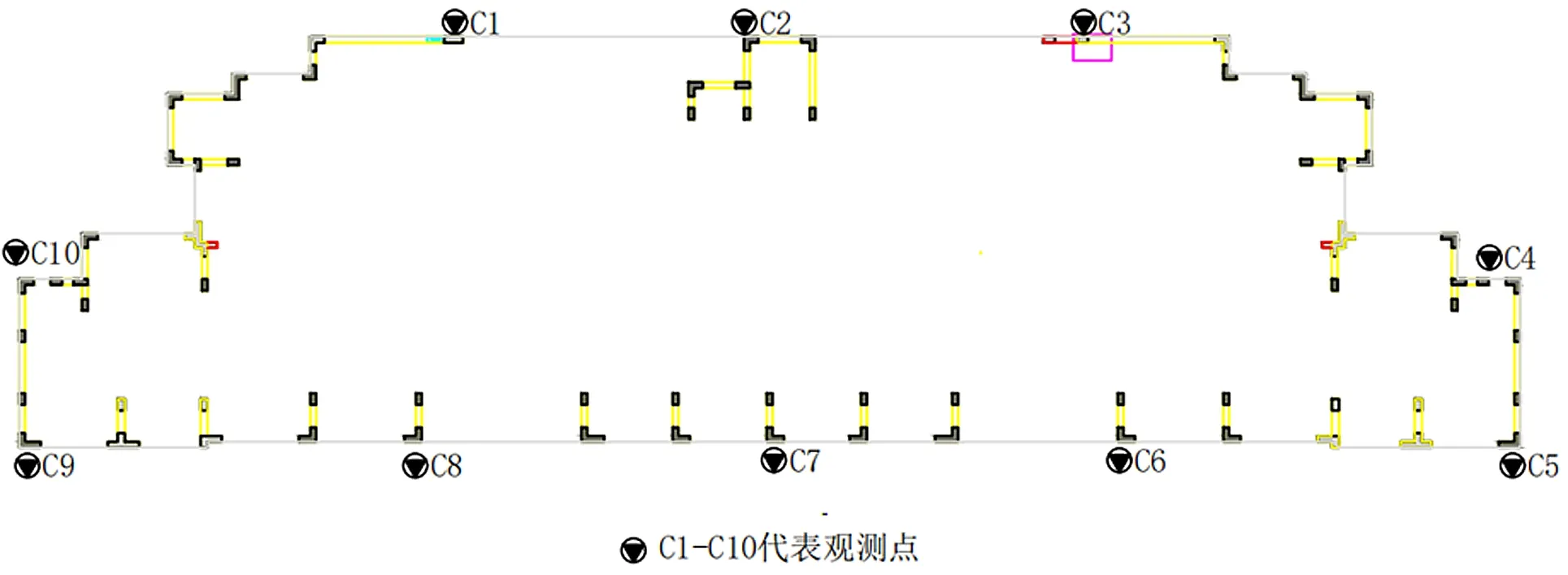
图1 工程示意图

该研究以二等沉降观测的要求为标准，监测点的测站高差中误差为0.5 mm，精度满足二等水准观测。根据建筑物沉降观测精度要求，本次外业观测采用的水准仪为天宝电子水准仪DINI03，观测方式采用往返观测，其中观测站为偶数站时采用前-后-后-前的顺序；奇数站时采用后-前-前-后的顺序。该项研究的数据为施工期间获取的数据，观测周期较为频繁。沉降的预警线为10 mm。

2 处理方法

2.1 原始数据

此次沉降数据为对周口恒大时代新城5#C3点进行了连续46 d的观测，每2天记录一次，数据如表1所示。

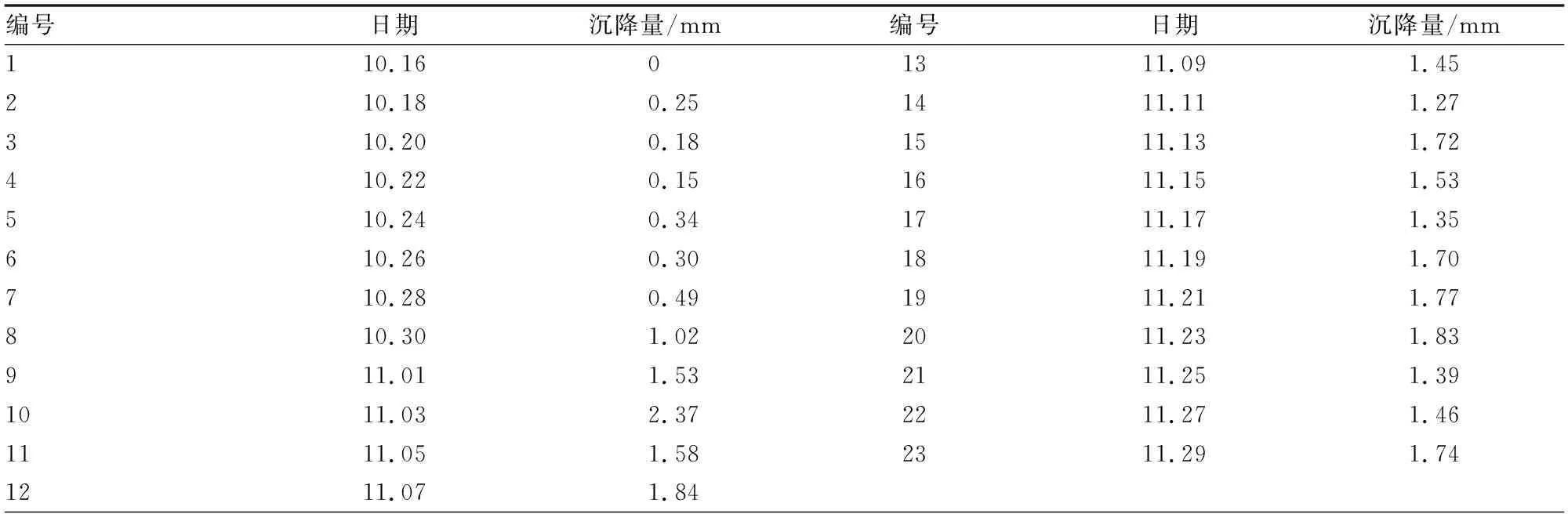
表1 10～11月沉降量观测数据

由表1可以看出，累计沉降量处于缓慢上升的状态，最后趋于平稳。在这个观测过程中，可能会产生一些误差，因此通过2种数学模型并结合平差的原则对数据进行分析，分析过程可以采用图2所示的流程方法。

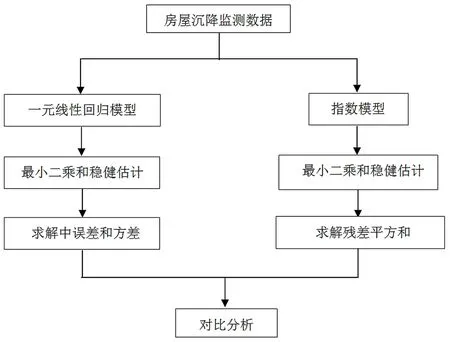
图2 流程图

2.2 建模方法

一元线性回归是回归模型中较为基础的回归模型，它是用来描述一个变量的变化对另一个变量变化的影响程度，该实验数据中含有2个变量，时间是自变量，累积沉降量是因变量，用数学形式表示出来

y=β0+β1x+ε

(1)

其中(β0+β1x)表示x对y的影响，β0和β1为未知参数，ε为不确定的随机因素对因变量y的影响，一般情况下随机因素ε是不可预测的。

为了估计模型参数，需要对变量进行n次观测，得到n组观测数据(yi,xi)(i=1,2,…,n)，代入方程(1)时有n个方程[4]:

yi=β0+β1xi+εi(i=1,2,…,n)

(2)

2.3 平差约束法则

利用最小二乘准则求未知数据，使这些数据与实际数据的误差平方和最小。

(3)

由此得到观测值yi的中误差为：

(4)

稳健估计中最为关键的是权函数的选择，根据残差值的大小来进行不同程度的降权，达到剔除粗差的效果。

M估计准则为：

(5)

误差方程为：

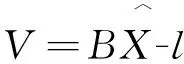
(6)

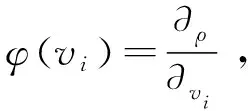
(7)

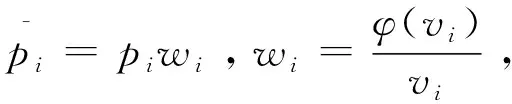
BTPV=0

(8)

将误差方程代入，可得M估计的法方程为：

(9)

(10)

3 实例分析

3.1 对比分析

以周口恒大时代新城某栋楼房的沉降数据为实验数据，由于在施工过程中沉降量随时间的变化可能是一种线性的关系，也可能是一种指数的关系，对此分别建立2种模型进行分析。图3为原始数据残差图，图4为原始数据拟合图，图5为指数数据残差图，图6为指数数据拟合图。

图3 原始数据残差图图4 原始数据拟合图

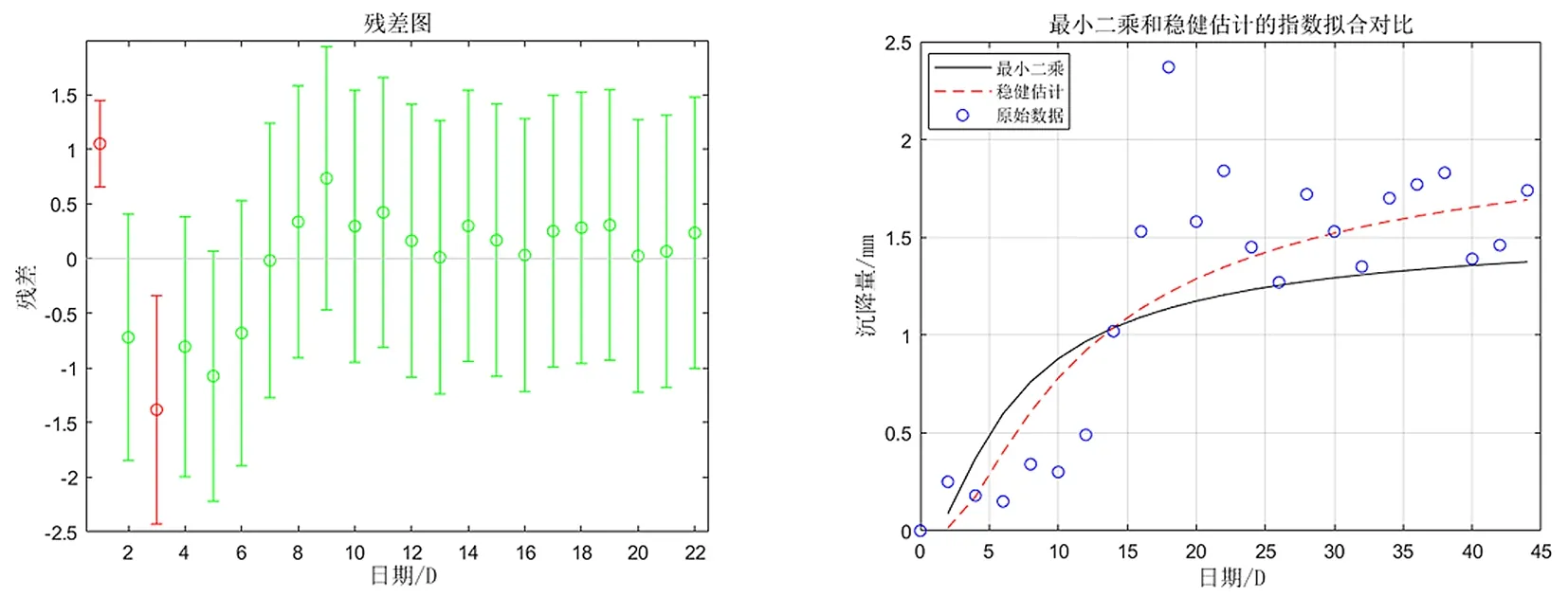
图3 指数数据残差图图4 指数数据拟合图

由最小二乘得到的系数为β0=0.331 3，β1=0.038 8，因此一元线性方程为：

y1=0.038 8x+0.331 3

(11)

由稳健估计得系数为α0=0.257 4，α1=0.039 8，因此稳健估计方程为：

y2=0.039 8x+0.257 4

(12)

表2所示为原始数据中2种方法的中误差和方差。

表2 原始数据中误差和方差

从图4可以看出，在含粗差的情况下，一元线性回归方程拟合的直线产生了较大偏差，而稳健估计的拟合直线只产生了微小的偏差。由表2可知最小二乘算得的中误差为0.454 4，稳健估计所得中误差为0.413 6，结合图像以及中误差，可得在有粗差的情况下，稳健估计的抗差性效果好于最小二乘法，其结果也更加准确[7]。

从图5可以看出，原始指数数据中含有粗差，基于含有粗差的情况，来分析最小二乘和稳健估计在指数模型中的抗差性。

由最小二乘法得到的系数为a0=0.419 6，b0=-5.653 2，因此指数方程为：

(13)

由稳健估计法得到的系数为a1=0.773 0，b1=-10.119 2，因此指数方程为：

(14)

表3所示为指数数据中2种方法的残差平方和。