超大型电磁振动试验设备水平滑台的建模分析及结构优化

杜环宇，李鸿光，孟 光，府晓宏

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.苏州东菱振动试验仪器有限公司，江苏 苏州 215010)

振动试验设备是一种能够产生特定频率范围内的振动并对其进行控制的振动测试系统，其主要任务就是通过一定的控制方式将需求的运动和能量传递给待测产品或零件，以模拟现实中的各种复杂环境对产品进行环境测试试验[1]。伴随着我国在载人航天、探月探火工程等国家重点工程的不断推进，各种航天结构需要面对、需要研究的动力学环境越来越复杂，也对振动试验设备提出了更高的要求，比如：更大的推力、更宽的测试频率范围。目前，东菱振动试验仪器有限公司的600 kN超大型电磁振动台已基本满足对航天器进行振动测试的推力要求，在进行整仓、整星振动试验时，由于空间和承载限制，一般需要将试件安装在配套的大型水平滑台上进行测试。

由于振动试验设备的重要性，电磁振动台又具有测试频率范围宽、加速度大且波形好的优点，很多学者都对电磁振动试验台开展了研究。例如：宦海祥等[1-2]以苏州试验仪器总厂VE-1031型电磁振动台为对象，采用MATLAB/Simulink仿真、振动试验、有限元模态分析相结合的方法，对振动系统的基本环节进行了理论分析和建模设计；范宣华等[3-4]对电磁振动台空台进行了系统有限元建模，并通过模态试验结果对仿真模型进行了修正；近年来，李红强[5]、张逸波等[6]、陈小慧[7]、夏天凉[8]、崔志磊等[9]、孟繁莹[10]、仝宁可等[11]分别利用Solidworks、Pro/ENGINEER和ANSYS、COMSOL、Patran等各类软件进行了电磁振动台结构的大量建模分析和结构设计工作，取得了重要研究成果。除了有限元分析方法，各种理论模型也被应用于研究电磁振动台结构中。例如：方政等[12-13]将动圈结构简化成圆柱壳结构，考虑对动圈简化模型圆柱壳外加加强筋，研究了动圈结构在工程中会产生的不稳定性问题；张奎华等[14]构建了驱动线圈、短路环及骨架的电路模型，推导出骨架动生和感生电流随频率变化的表达式并进行了热功率计算。

可以看到，由于系统复杂性，与电磁振动台相关的研究工作主要是依靠有限元等数值方法开展的，并且绝大多数是研究动圈这一振动台主要部件。虽然动圈结构确实是决定振动试验设备测试频率范围的核心部件之一，但实际上，在进行水平振动试验时，水平滑台结构的轴向共振频率同样对设备能够进行测试的频率范围有着重要制约。为了保证振动试验设备在水平测试过程中输出准确的振动形式，水平测试的频率一般需要在滑台轴向共振频率以下，远低于振动台本身的工作频率上限。因此，对水平滑台进行分析研究和结构优化，提高该结构的轴向共振频率，才能够进一步拓宽超大型电磁振动试验设备的测试频率范围，提升对航空航天领域大型试件进行测试的能力。

由于超大型电磁振动试验设备配套的水平滑台本身也是个复杂结构，而且由于滑板尺寸较大，其在实际制造中是采用分部件加工，再将各部件通过螺栓连接组成。所以在进行分析时，需要考虑螺栓连接形式对结构分析结果的影响。目前，国内外很多学者都提出了一些针对螺栓连接形式的仿真方法。例如：杨国庆等[15]提出了结合有限元分析与插值计算的螺栓连接刚度理论计算方法；Zhao等[16]提出了一种基于修正三维分形形貌的螺栓联接刚度阻尼模型；黄开放等[17]、田红亮[18]、Ye等[19]、Liao等[20]、Xiao等[21]分别提出了各种基于虚拟材料方法发展改进而成的螺栓连接模型，并将其应用在理论分析或有限元仿真工作中；Nassar等[22]提出了改进的螺栓连接模型，其中采用一种新的方法来获得螺栓连接中的有效面积表达式。然而，由于这些方法都比较复杂，不容易直接应用在水平滑台这种复杂实际结构上，所以，本文在此基础上采用了一种更易于建模分析的螺栓连接仿真方法，并通过模型分析结果与试验结果的对比验证了其有效性。

1 水平滑台的有限元分析

1.1 主要结构建模

去除水平滑台上安装孔、工艺圆角等对整体动力学特性影响较小的细节结构，超大型电磁振动试验设备的水平滑台主要结构部件，如图1所示。主要包括有：①牛角夹持头，水平滑台通过该部件与电磁振动台台面相连，以传递运动和能量；②前-后滑板，因为该水平滑台台面面积大，很难一体加工成型，所以分为前、后两部分滑板加工而成，在通过螺栓连接在一起，另外前滑板与牛角夹持头进行连接；③静压导轨，静压导轨通过压力油承载水平滑台以及安装在水平滑台上的试件，同时对运动中的滑台起导向作用。根据实际情况，该滑台底部共计布置了10×10个静压导轨。为了更加准确地模拟实际情况，同时还建立了振动台动圈结构的空心圆柱体模型，将其连接在牛角夹持头前部。各部件组装后，完整水平滑台结构如图2所示。

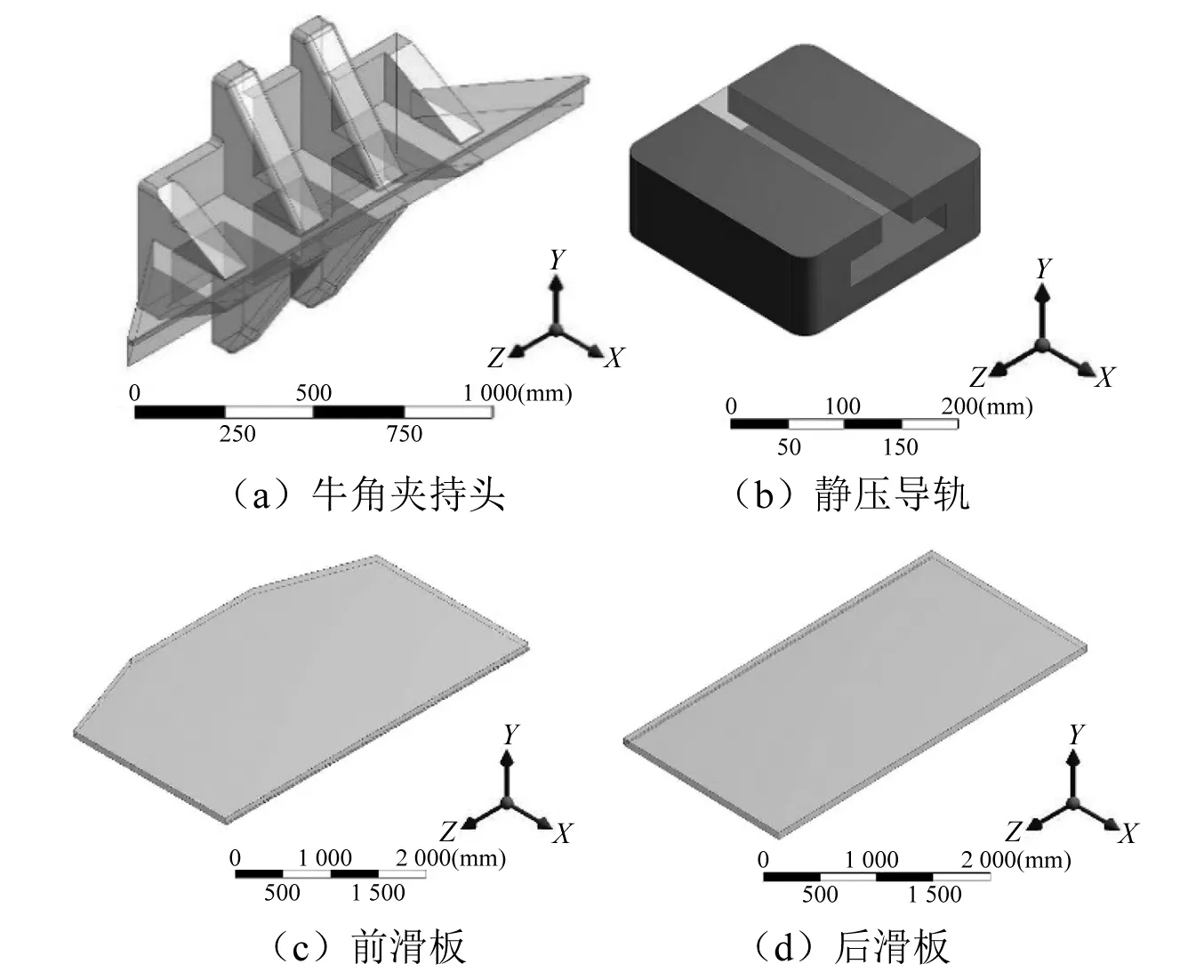
图1 超大型电磁振动台水平滑台主要部件示意图

图2 组装后的水平滑台总体结构示意图

该水平滑台各部件均采用7075铝合金制造加工而成，连接螺栓材料为普通结构钢。模型中所使用的材料属性及主要结构尺寸参数，具体如表1所示，在表1中:统一将X轴方向的尺寸称为长度、将Y轴方向的尺寸称为厚度、将Z轴方向的尺寸称为宽度；将前滑板前端有斜度的部分称为前滑板连接部。

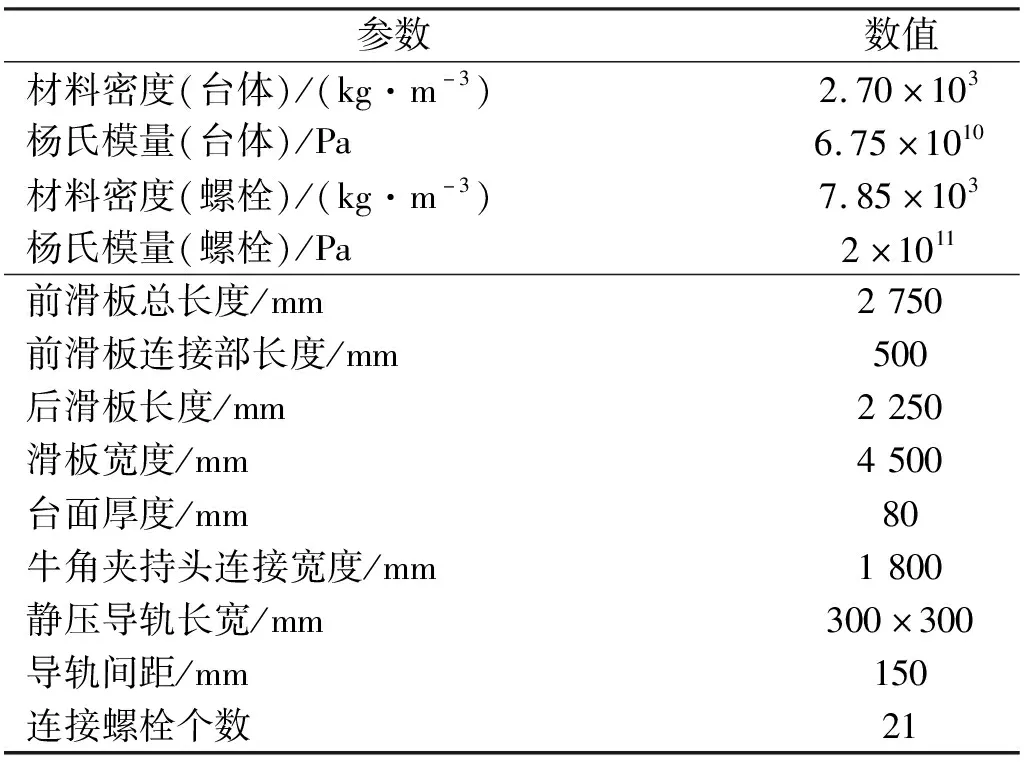
表1 水平滑台结构模型主要参数表

1.2 接触面约束及连接形式定义

水平滑台在正常工况下，只在牛角夹持头处受到水平方向的振动台台面激励而产生水平(沿X轴方向)振动，垂直方向(沿Y轴方向)的振动极小。因此，在界面定义与分析过程中，主要关注滑台本身在轴向、即X轴方向的动力学特性。因此,为了简化分析过程，将前后滑板与静压导轨T型内导板之间的垂直向连接近似为完全刚性连接，而对牛角夹持头-前滑板、前-后滑板间的螺栓连接进行详细建模，以得到准确的水平滑台轴向模态。其中，牛角夹持头-前滑板间的螺栓选用的是M14型号，而前-后滑板间选用的是M16型号。

本文以牛角夹持头-前滑板间的相邻界面为例说明研究中采用的简易螺栓连接模型，前-后滑板间的相邻界面模型建立同理。在实际情况下，接触面之间存在连接刚度的区域可以被认为只存在于螺栓连接的部分接触面处。一般认为，螺栓连接部分的法向刚度包括螺栓本身的刚度和被连接件的刚度，如图3所示。在本文里，为了简便，螺栓连接模型的接触面直径被直接建模为螺栓直径，如图4所示，因此有必要通过定义法向刚度修正系数(normal stiffness factor，NSF)进行修正。将接触面之间存在连接刚度的被连接件区域认为是跟螺栓有所接触的区域，即被连接件单元的法向刚度为

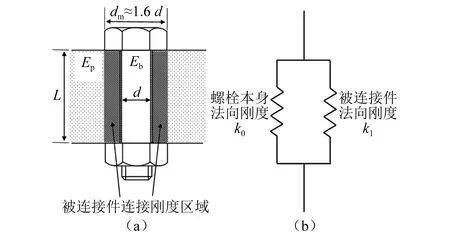
图3 螺栓连接部分法向刚度等效示意图

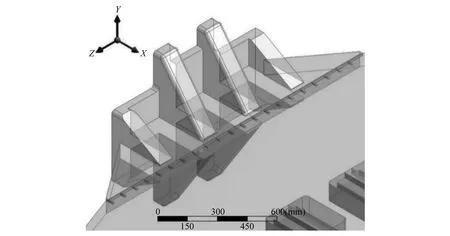
图4 含螺栓连接的牛角夹持头-前滑板相邻界面示意图

(1)

同样的，螺栓本身单元的法向刚度为

(2)

即螺栓连接部分的总法向刚度应为上述两部分刚度之和，代入数值进行计算可得

(3)

dk=dk0+dk1=(1+αNSF)×dk0≈1.5×dk0

(4)

式中：Ep和Eb分别为台体和螺栓材料的杨氏模量；d为连接螺栓的公称直径；dm为连接螺栓的螺帽直径；dk1，dk0和dk分别为被连接件单元法向刚度、螺栓单元法向刚度和螺栓连接部分的总法向刚度；αNSF为法向刚度修正系数。

由于在建模分析中，法向刚度被认为只集中在螺栓模型接触面上，所以在分析模型中，将其法向刚度修正为原法向刚度的1.5倍再进行仿真分析。因为非轴向特性不是本文关注的重点，所以在分析时将21个螺栓模型周向均设置与夹持头或滑板的完全刚性连接。

除了上述两个接触面螺栓连接形式定义以外，在对模型进行仿真计算前，还需要定义该水平滑台受到的实际边界约束条件。水平滑台作为振动试验设备中的运动件，其受到的边界约束主要有两种：第一种，在振动台动圈处受到的导向约束。振动台台体中通过加装导向装置、悬挂装置等，保证动圈结构只能进行轴向(沿X轴方向)振动。因此，在仿真分析里，在动圈模型外表面添加如图5所示的边界约束，只保留X轴方向的自由度。第二种，在T型静压导轨处受到的边界约束。其中，外导轨底部与基台固结，限制了该面的所有方向自由度；T型内导板和外导轨之间充满了润滑油，限制了除X轴方向之外其他方向的自由度，而在X轴方向可以认为是无摩擦滑动。具体操作中，每个静压导轨处所添加的约束条件，如图6所示。

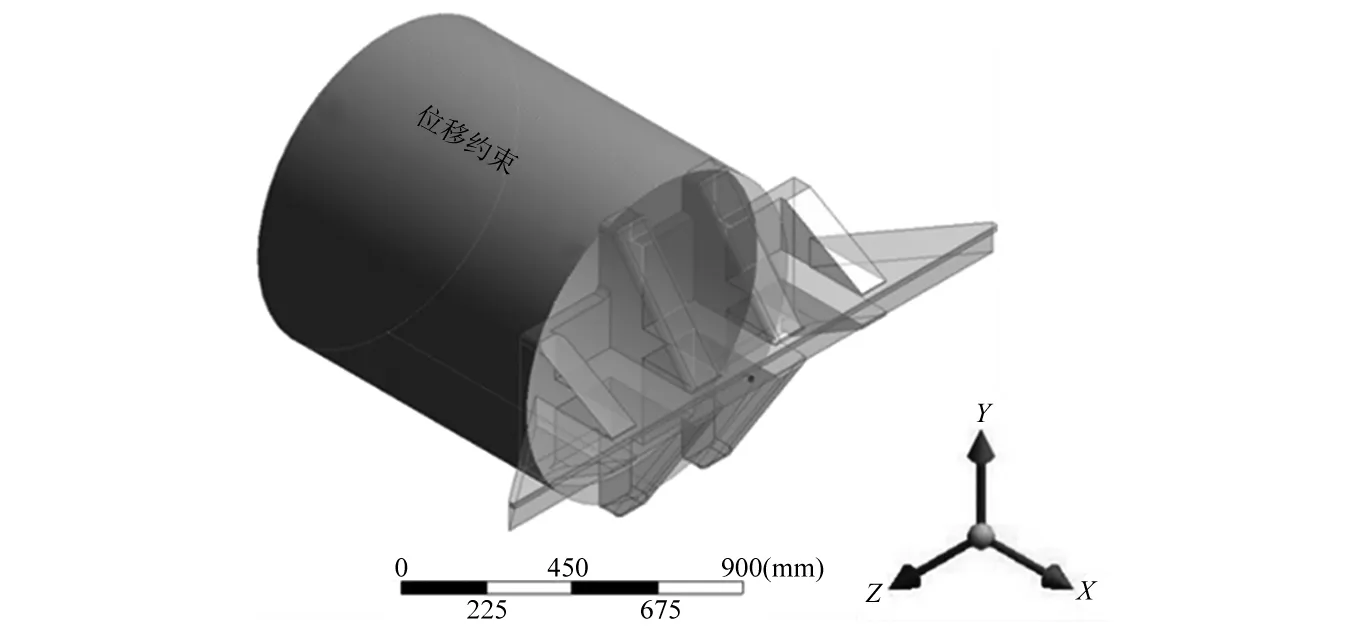
图5 动圈模型外表面添加的导向约束

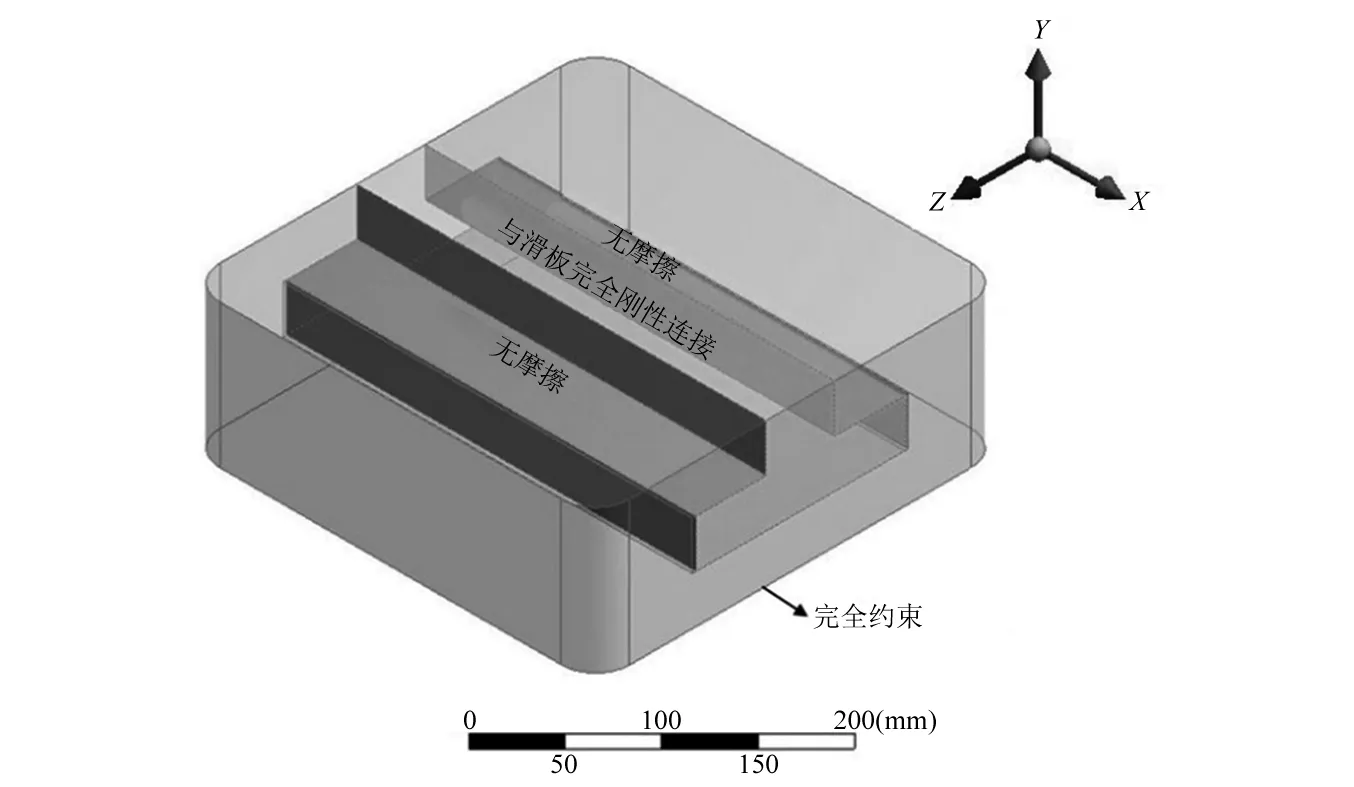
图6 每个静压导轨处添加的约束条件

2 计算结果及振型分析

采用ANSYSWorkbench 16.0中的模态分析模块对完成了上述设置的振动试验装置水平滑台有限元模型进行网格划分和模态分析，求解该结构的前10阶振型和固有频率。除去第1阶刚体模态，第2～第9阶固有振型如图7所示，其对应的固有频率如表2所示。

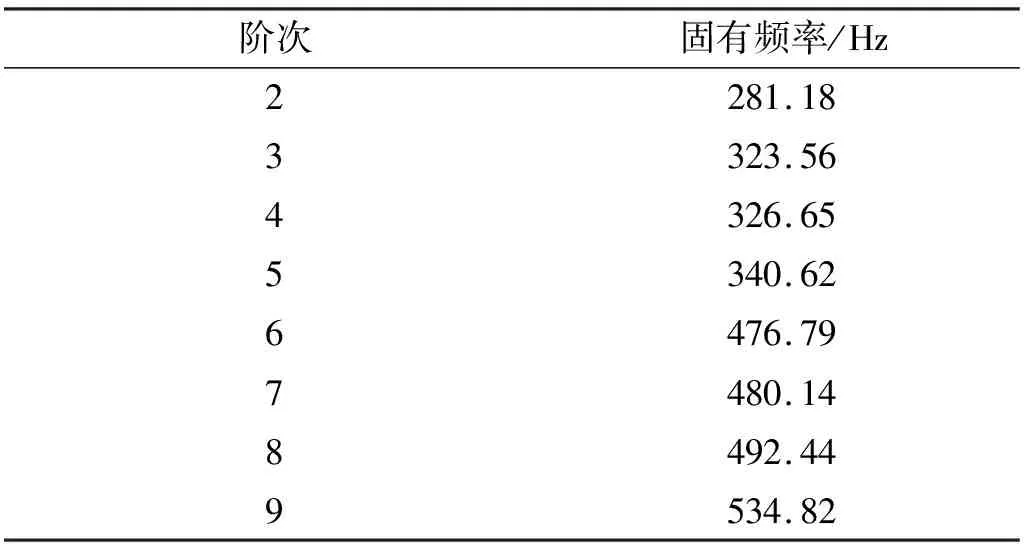
表2 水平滑台结构第2～第9阶固有频率

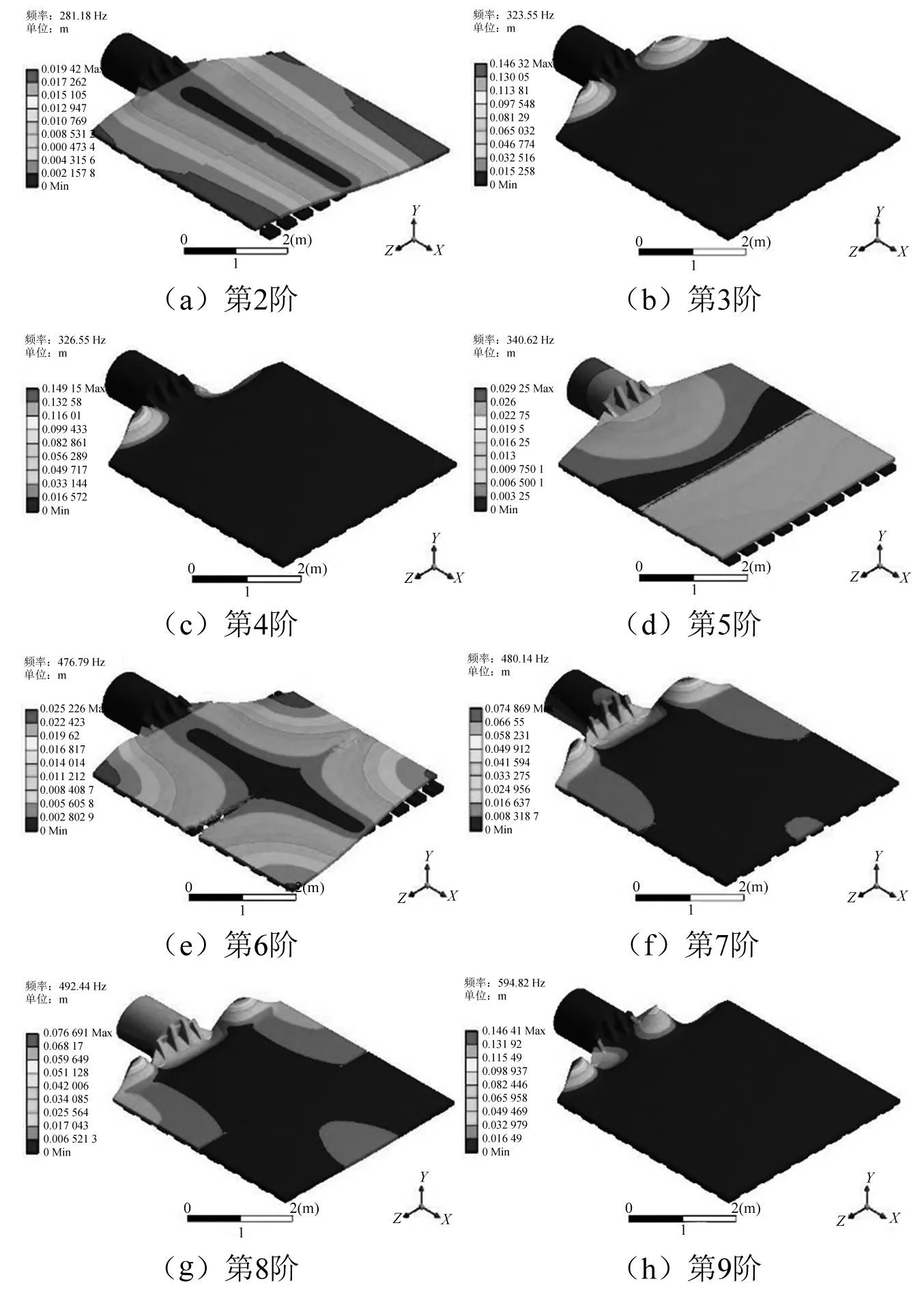
图7 水平滑台结构第2～第9阶固有振型

根据上述模态分析结果，可将该水平滑台结构的振动特性总结如下：

(1)水平滑台结构的低阶振型主要是在牛角夹持头-前滑板部位发生，在前10阶振型中有第3、第4、第7、第8、第9阶振型，包括了牛角夹持头-前滑板连接部的上下摆动、绕X轴的扭转等。然而，这些模态振型对水平滑台整体及其上安装的待测工件的影响比较有限。在实际测试中，待测工件一般安装在水平滑台中央，这些局部模态很难传递到该位置。

(2)在上文的约束条件情况下，水平滑台结构整体在280 Hz以上即有可能发生绕Z轴的扭转，如前10阶振型中的第2、第6阶振型。这两阶振型不属于局部振型，若激发出该振型会对台面上的待测工件产生比较大的影响。因此，需要通过对前-后滑板两侧增加限位槽的方法防止它们发生。

(3)在这些分析结果中，只有第5阶振型是水平滑台结构整体沿轴向(X轴方向)的伸缩振动，同样会对台面上的待测工件产生不良影响。另外，不同于第5、第9阶那样的绕Z轴的扭转振型，该轴向伸缩振型难以通过简单地增加滑台约束的方式进行防止，只能通过对结构本身进行设计和优化来改变。所以，该轴向伸缩振型是本研究中的重点关注，该固有频率也就是所谓的水平滑台结构的一阶轴向共振频率，对该水平滑台的振动测试频率范围起决定性作用。

为验证本文有限元分析结果的有效性，对该水平滑台样件进行了扫频测试。测试结果说明该水平滑台结构的一阶轴向共振频率为342.5 Hz，与分析结果340.62 Hz非常接近，相对误差仅约0.55%，验证了模型的有效性。另外，本文还对比了不建立螺栓连接模型的水平滑台结构分析结果，其计算出的一阶轴向共振频率为384.64 Hz，相对误差明显更大，说明了在结构建模分析中建立螺栓连接模型的必要性。

3 水平滑台结构的优化设计

既然振动试验装置水平滑台的一阶轴向共振频率是制约测试频率范围的重要指标，且它是由水平滑台结构本身决定的。因此，对水平滑台结构进行优化设计以提高一阶轴向共振频率就具有重要意义。首先，需要进行各主要结构尺寸的灵敏度分析。

3.1 灵敏度分析

灵敏度分析方法主要研究某模型参数(x)对分析目标(y)的影响程度，从而选取出某些待优化参数、同时确定这些参数的初始优化方向。本研究中，在对水平滑台结构的优化过程中，主要目标是提高其一阶轴向共振频率(第5阶固有频率)，同时不希望结构质量增加太多而降低可用推力。因此，本文中各尺寸参数的灵敏度包括频率灵敏度和质量灵敏度两部分。

由于牛角夹持头的前端要与振动台台面相连、静压导轨要与设备基台固结，对这两部件尽量不做修改。所以，本文在分析中选取的尺寸参数有：台面厚度(h)、牛角夹持头连接宽度(ds)、前滑板连接部长度(ls)、牛角夹持头-前滑板连接螺栓直径(Ø1)以及前-后滑板连接螺栓直径(Ø2)。需要指出的是，虽然螺栓直径在选型时应当是离散的，但为了分析方便，本部分仍然将其作为连续参数进行分析。上述各参数对一阶轴向共振频率及质量的全局灵敏度曲线，分别如图8～图11所示。其中，由于螺栓尺寸对整个水平滑台结构影响极小，所以只展示了对一阶轴向共振频率的灵敏度曲线。

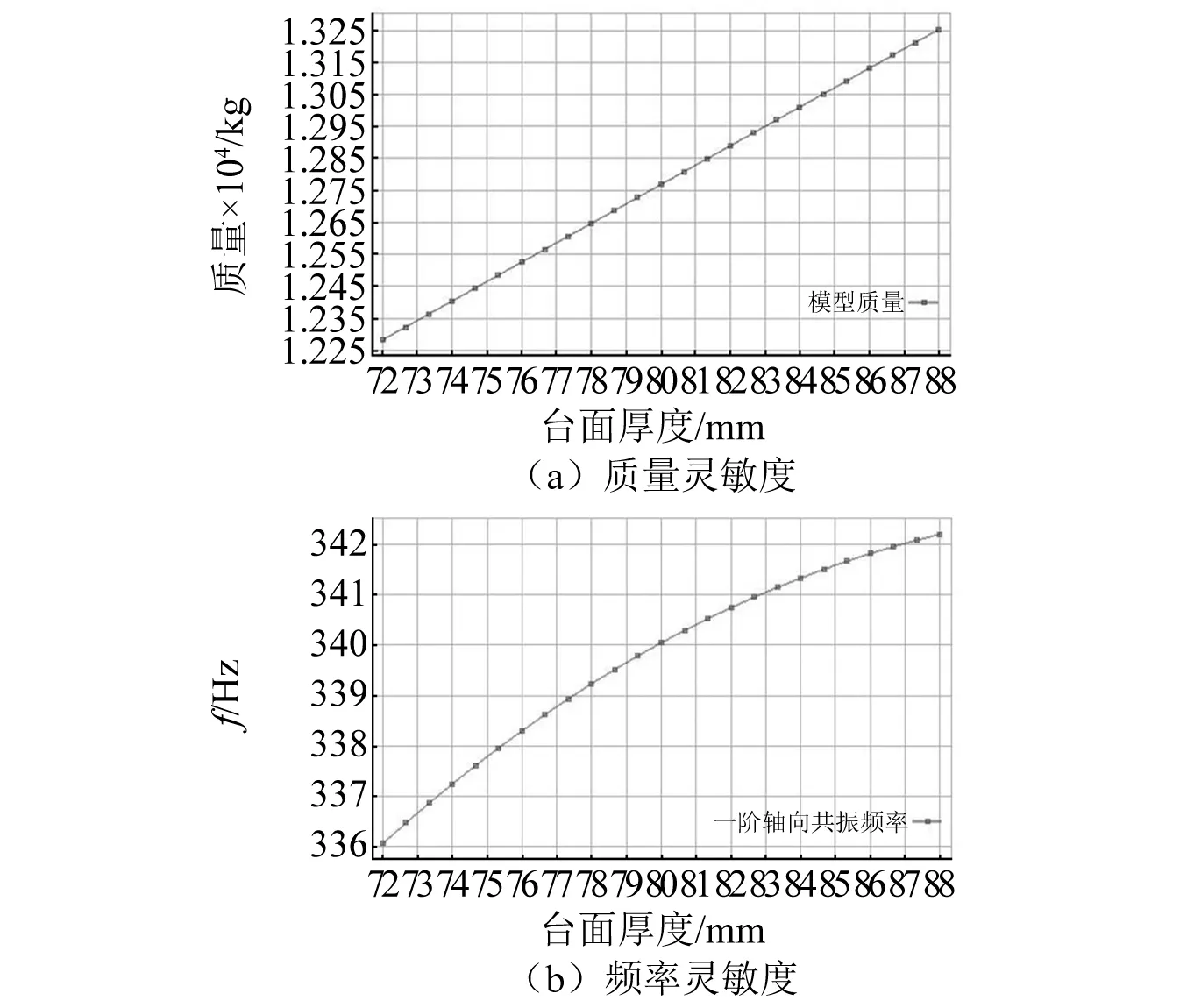
图8 台面厚度(h)的灵敏度结果

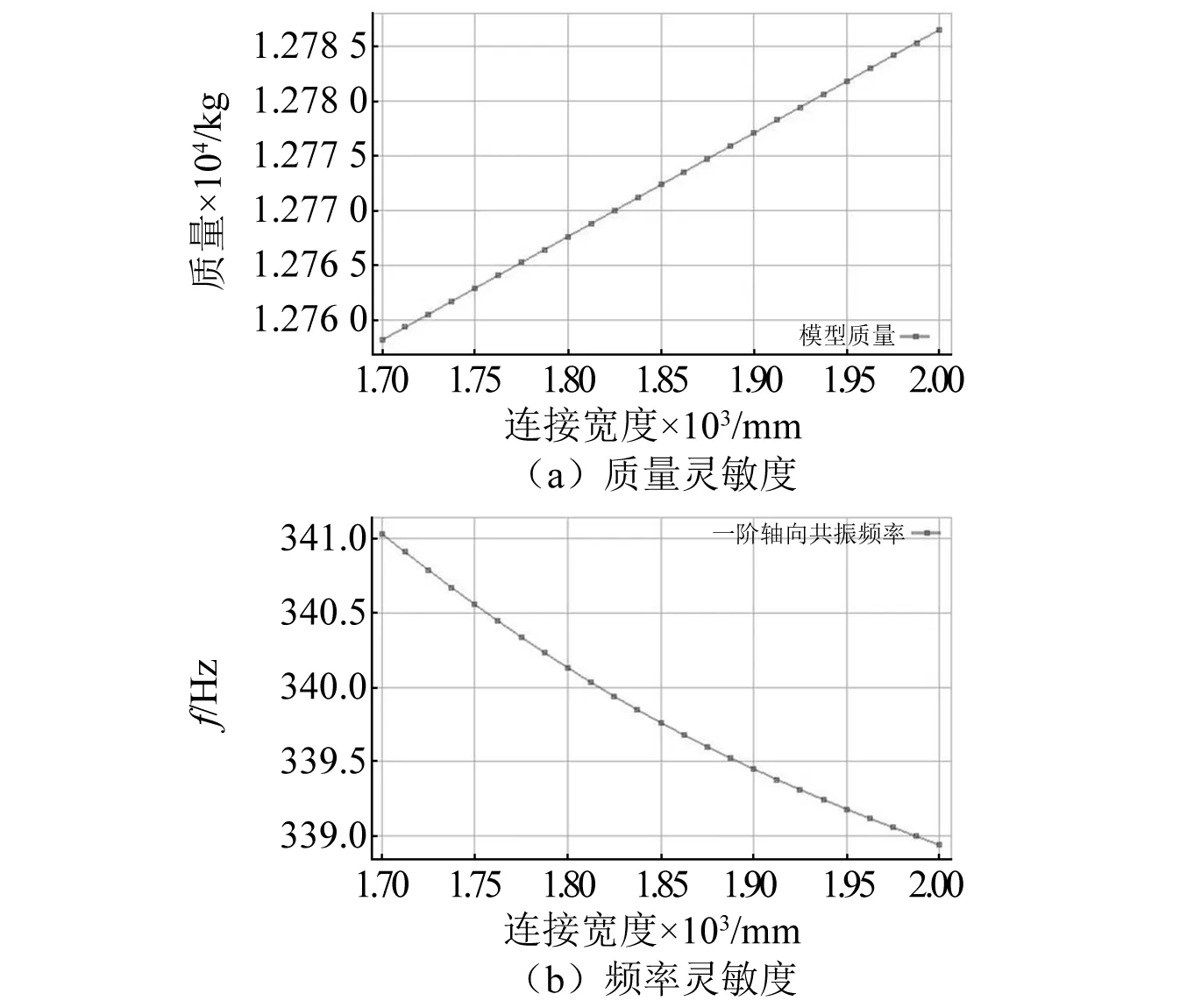
图9 牛角夹持头连接宽度(ds)的灵敏度结果

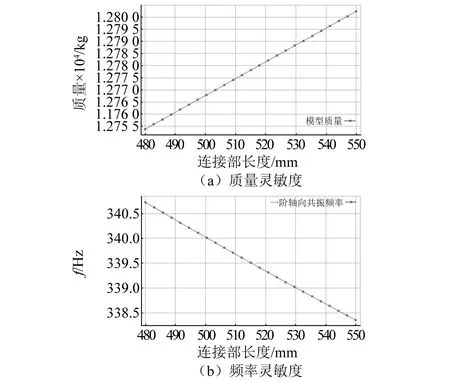
图10 前滑板连接部长度(ls)的灵敏度结果

图11 连接螺栓直径的灵敏度结果

在水平滑台各参数初始尺寸处(见表1)，参数的局部灵敏度具体数值和对比如表3(质量灵敏度)和表4(轴向频率灵敏度)所示。由于水平滑台结构各尺寸的数量级差别较大，因此除了传统的灵敏度数值以外，在表3中还使用了百分比灵敏度数值，即该尺寸参数每变化1%对分析参数的影响程度。根据灵敏度分析结果，各个尺寸参数对结构质量、一阶轴向共振频率的影响分别如下：

(1)水平滑台结构的台面厚度(h)与结构质量、一阶轴向共振频率均为正相关。由表3可知，h的增大会显著增加水平滑台的质量，质量灵敏度是其他参数的80倍以上，质量百分比灵敏度是其他参数的10倍以上；然而，由表4可知，h的增大对一阶轴向共振频率的影响并不像对质量的影响那么显著，频率百分比灵敏度与其他参数相当，且影响程度在不断减弱(见图8(b))。因此，考虑到水平滑台结构的质量限制，在后续的最终优化方案中，没有将台面厚度(h)作为需要优化的尺寸参数。

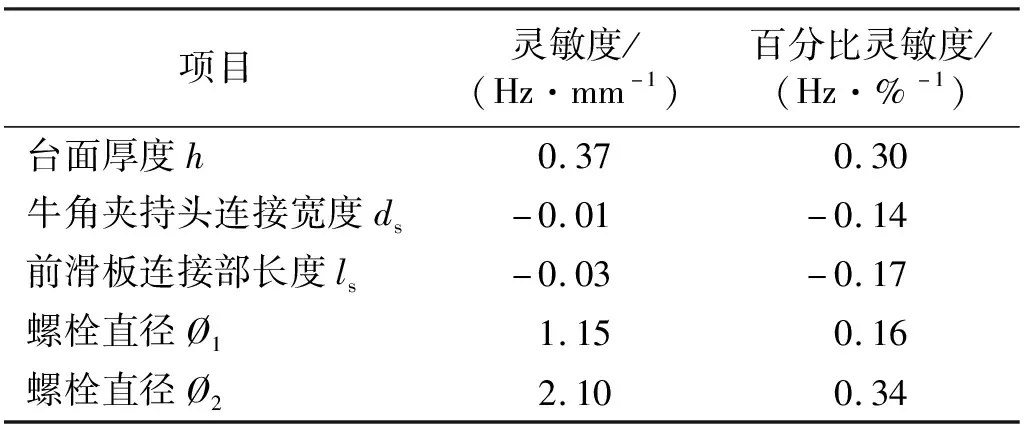
表4 水平滑台结构各尺寸参数的局部灵敏度数值(频率)

(2)牛角夹持头连接宽度(ds)和前滑板连接部长度(ls)分别与水平滑台结构质量为正相关、与一阶轴向共振频率为负相关，即对这两个尺寸参数进行优化，不仅能够提高水平滑台的一阶轴向共振频率，还能够进一步降低结构质量、提高可用推力。因此，它们是后续优化过程中需要优化的尺寸参数。其中，前滑板连接部长度(ls)对一阶轴向频率的百分比灵敏度更大，达到了-0.17 Hz/%。

(3)牛角夹持头-前滑板连接螺栓直径(Ø1)和前-后滑板连接螺栓直径(Ø2)与一阶轴向共振频率为正相关。同时，由于螺栓本身相比于水平滑台整体尺寸非常小，因此对结构质量的改变也很小，其百分比灵敏度在10-3数量级，远小于其他尺寸参数，基本可以忽略不计，所以在表3中没有列出。螺栓直径Ø1和Ø2对一阶轴向共振频率的影响比较明显，百分比灵敏度分别为0.16 Hz/%和0.34 Hz/%，即对这两个尺寸参数进行优化，能够在不显著改变结构质量的前提下显著提高一阶轴向共振频率。另外，相比于其他尺寸参数，螺栓直径能很容易的改变甚至100%。因此，它们也是后续优化过程中需要优化的尺寸参数。

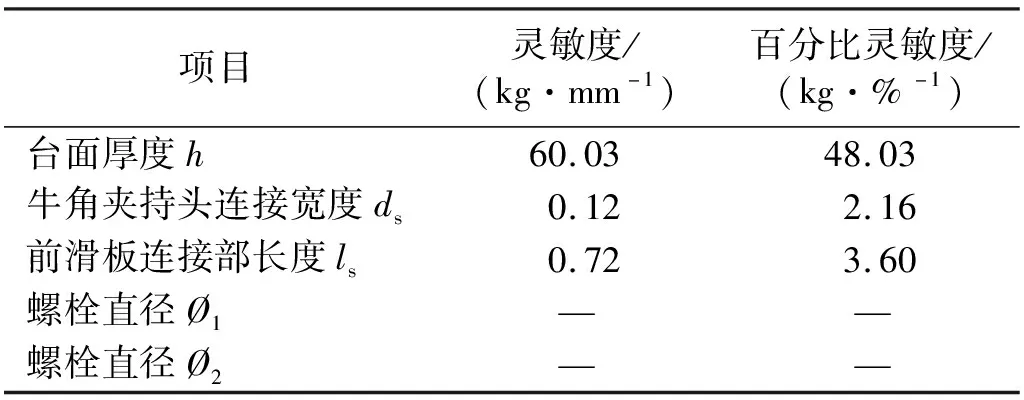
表3 水平滑台结构各尺寸参数的局部灵敏度数值(质量)

3.2 优化结果和讨论

根据水平滑台结构的实际情况，最终对各个待优化尺寸参数优化范围选择，以及最终通过ANSYS Workbench 16.0的各参数响应面联合优化结果，如表5所示，优化后的水平滑台结构总质量(不包含导轨)为5 107.22 kg，相比原结构降低了0.97%，基本维持不变；一阶轴向共振频率为369.69 Hz，相比原结构提高了8.72%，优化后的水平滑台结构一阶轴向振型如图12所示。

表5 水平滑台各优化参数的优化范围及结果

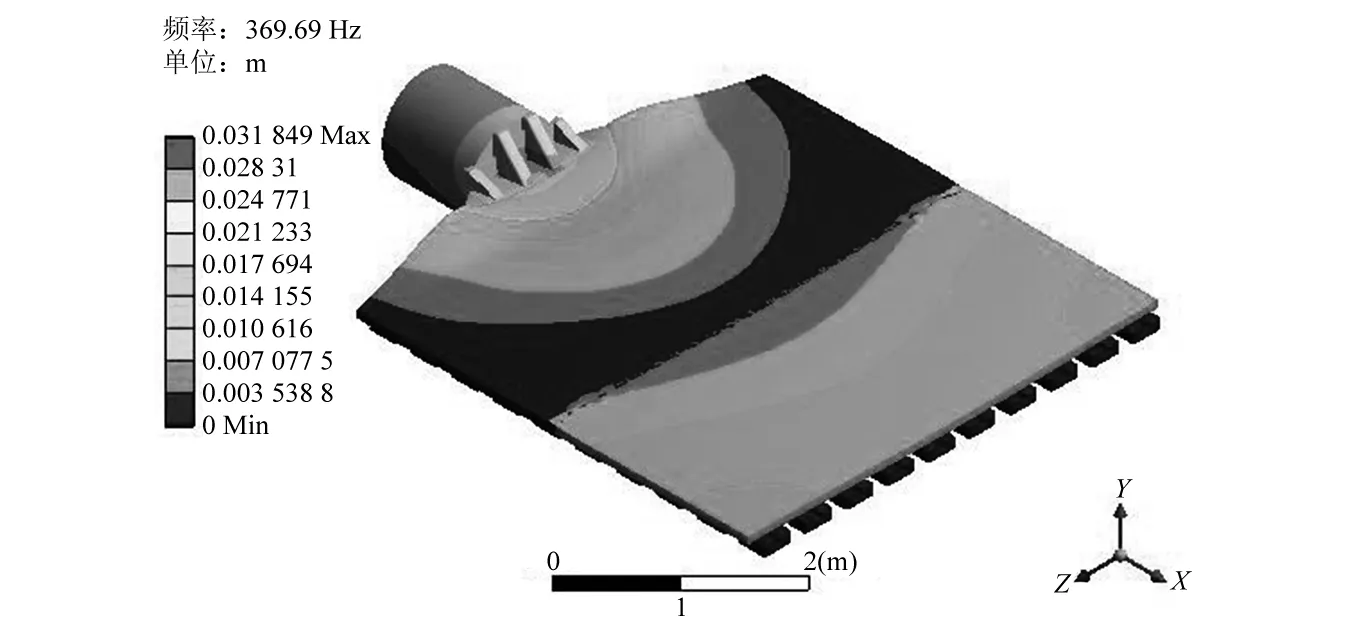
图12 优化尺寸后的水平滑台一阶轴向振型

根据上述分析和优化结果可知，为了提高水平滑台结构的一阶轴向共振频率，关键措施之一就是将牛角夹持头-前滑板、前滑板-后滑板之间的连接螺栓改用直径(Ø1和Ø2)更大的型号。这是由于当选用直径更大的连接螺栓，实际连接的接触面面积也越大，接触面间的轴向平均总刚度越高，从而提高了结构整体的轴向共振频率。同样地，如果能在不损伤螺栓和接触面的前提下增加每个螺栓接触面的法向接触刚度，如增加螺栓预紧力等措施，也能够提高水平滑台结构的轴向共振频率。另外，减轻动圈部分的质量同样有利于提高结构的一阶轴向共振频率。

4 结 论

本文针对东菱振动试验仪器有限公司600 kN推力超大型电磁振动试验设备的水平滑台为对象，在ANSYS Workbench 16.0中采用有限元分析方法对其结构的轴向共振进行研究。通过对水平滑台的各部分结构进行详细的建模，并在各接触面上使用了一种简易有效的螺栓连接模型，使得仿真分析的准确度大大提升。通过该水平滑台模型得出的一阶轴向共振频率结果与试验测量结果之间的误差仅为0.55%。

在该建模分析的基础上，本文进一步研究了在不明显降低可以推力的前提下、提高水平滑台结构一阶轴向共振频率的优化设计方案，以进一步拓宽超大型电磁振动试验设备的测试频率范围。优化分析的结果总结如下：

(1)在对水平滑台本身结构尺寸的优化中，对牛角夹持头连接宽度(ds)和前滑板连接部长度(ls)的改变更加有效，不仅能够提高一阶轴向共振频率、还能够降低结构质量；台面厚度(h)的改变虽然也能够提高一阶轴向共振频率，不过同时会显著增加结构质量，不宜作为优化设计的考虑因素。

(2)牛角夹持头-前滑板之间的螺栓连接、以及前-后滑板之间的螺栓连接对水平滑台结构的一阶轴向共振频率有关键影响，尤其是前-后滑板的螺栓连接。通过选用更大直径(Ø1和Ø2)的连接螺栓、提高每个连接螺栓的预紧力等方式，能够显著提高水平滑台结构整体的一阶轴向共振频率，同时对结构质量几乎没有影响。另外，也可以考虑在结构工艺上对牛角夹持头-前滑板、前-后滑板的接触面之间进行焊接、加固等，进一步提高轴向共振频率。

(3)仅对水平滑台结构的尺寸参数进行优化，在本文所选取的参数优化范围(见表5)中，可将其一阶轴向共振频率提高到369.69 Hz，而且将其结构总质量降低49.54 kg，保证了振动试验设备的可用推力不减小。