基于GA-BP和PSO-BP神经网络的间冷塔扇区出水温度预测研究
2022-01-04周慧陈宪刚周宏贵胡蓉何永斌
周慧,陈宪刚,周宏贵,胡蓉,何永斌
(1.湖南大唐先一科技有限公司,湖南 长沙 410004;2.华能八〇三热电厂,甘肃嘉峪关 735100)
0 引言
间接空冷凝汽技术能够有效地解决缺水地区的火力发电问题,在我国北方地区被广泛应用[1]。但是,面对变化多端的外界环境(风速、风向、环境温度等),在北方冬季环境温度过低时,大部分电厂都面临着间冷系统散热器结冻的问题,严重威胁电厂的安全生产。为了解决间接空冷机组运行中存在的散热器冷却柱结冻的问题,李彦军等[2]提出了新颖的防冻理念,为高寒、高海拔地区间冷系统散热器结冻制定了防冻措施。梁娅莉等[3]提出了高海拔地区间冷系统设计应当考虑的因素与措施。李昊等[4]搭建了散热器冲洗决策模型,利用粒子群优化BP神经网络算法对间冷塔出水温度进行了预测。这些研究都为电厂安全稳定运行提供了强有力的技术支持。
某电厂330 MW超临界机组采用表凝式间接空冷系统,配置85个冷却三角,分为6个冷却扇段,每个扇段包含14~15个冷却三角。根据该电厂实际的运行经验,在极寒温度条件下,散热器冷却柱容易发生结冻,主要原因包括:散热器冷却柱内部流体流速过低,管内流体以层流为主,导致金属表面接触的流体温度急剧降低,从而发生局部结冻事故;由于受到间冷塔周边风速、风向、光照条件等因素影响,导致散热器冷却柱内部流体的流速和温度分布差异大;冬季极端低温度下启机,由于散热器冷却柱散热面积大且表面温度过低,因而充水温度下降,导致冷却柱结冻。
对该电厂330 MW超临界机组实际运行过程中结冻的原因进行分析,发现间冷塔扇区出水温度是防止冷却柱结冻最重要的控制参数,因为该参数能够更加直接地反应散热器壁面温度、内部流体流速和散热情况。通过对该机组DCS中的实时运行数据进行分析,综合考虑风速、循环水流量、冷却塔空气质量流量、环境温度、机组负荷等因素,分别采用BP、GA-BP、PSO-BP三种神经网络算法构建间冷塔扇区出水温度预测模型,实现对间冷塔扇区出水温度的预测,为电厂运行人员争取更多时间以采取措施保证扇区出水温度在最低允许温度之上,达到“治未病”的效果。同时,也为散热器结冻故障预警及诊断提供有效的判断依据。
1 间冷塔扇区出水温度的影响因素
间接空冷系统扇区出水温度受多种因素的影响,这些因素彼此之间既相互联系又相互制约,在不同外界环境条件下,各因素的影响也会发生变化。为了更加准确地描述扇区出水温度与各个因素之间的关系,选取该机组2019年12月的运行数据为样本数据,每隔5 min采集一组数据,共计8 329组数据。通过计算灰色关联度对采集的实时数据进行相关性分析。
根据电厂的实际情况,循环冷却水流量、冷却塔空气质量流量测量不准确。因此,循环冷却水流量的影响由循环水泵电流、扇形段顶部压力、旁路阀压差表征,冷却塔空气质量流量的影响由大气压力、环境风速、百叶窗开度等进行表征。通过计算得出的扇区出水温度与各因素的关联度见表1。

表1 扇区出水温度与各因素的关联度
灰色关联度分析的结果表明,冷却塔进水温度与扇区出水温度的关系最密切,关联度为0.855 3;其次,扇形段冷却柱表面温度、循环水泵电流、环境温度、扇形段百叶窗开度等与扇区出水温度的关系也很密切,其关联度系数也很大。
2 预测模型搭建
2.1 BP神经网络
BP(Back Propagation)神经网络是一种采用误差反向传播的前馈神经网络模型,具有良好的自组织学习能力,能够对大规模数据进行并行处理。模型由一个输入层、一个输出层和若干中间的隐含层组成。输入层、隐含层、输出层之间分别采用权重和激励函数连接与传递[5-7]。BP神经网络的结构如图1所示。
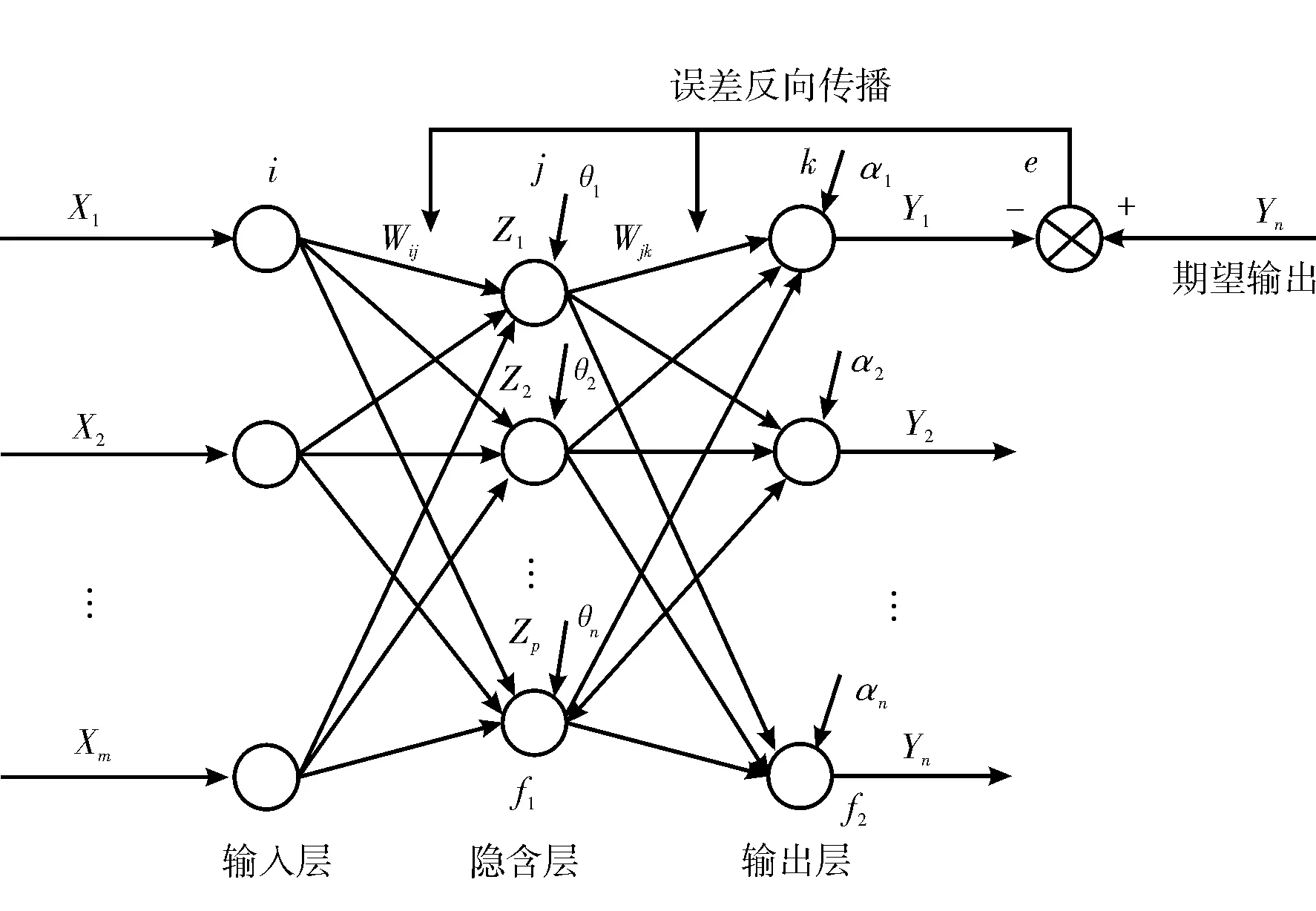
图1 BP神经网络基本结构
如图1所示,X1、X2、...、Xm表示m个输入层神经元;Y1、Y2、...、Yn表示n个输出层神经元;Z1、Z2、...、Zp表示p个隐含层神经元;θ1、θ2、...、θn表示隐含层各神经元的阈值;a1、a2、...、an表示输出层各神经元的阈值;Wij为输入层与隐含层的连接权值;Wjk为隐含层与输出层的连接权值[8]。
当神经元收到的信息达到阈值时,神经元就会通过激活函数激活,常见的激活函数包括:逻辑函数Sigmoid、双曲正切函数tanh、线性整流函数ReLU。本文中采用逻辑函数Sigmoid作为激活函数,其表达式为:

基于扇区出水温度影响因素的分析结果,选取冷却塔进出温度、扇形段冷却柱表面温度(8个)、扇形段百叶窗开度(7个)、循环水泵电流、环境温度等28个参数作为模型输入变量;扇区出水温度为输出变量,对机组6个扇区的出水温度分别进行建模和预测。隐含层数目由公式(2)确定为10。因此,神经网络结构为28-10-1。

式中,m为神经网络输入层个数;n为神经网络输出层个数,a为1~10中的任意整数。
2.2 GA-BP神经网络
遗传算法(Genetic Algorithm)是基于生物进化原理的一种多点搜索全局性优化算法。按照一定的适应度函数处理种群中的个体,对适应度高的个体进行生物遗传中的选择、交叉和变异,不存在求导和函数连续性的限定,不需要确定规则自适应的搜索全局最优解。参数编码、设定初始种群、设计适应度函数、设计遗传操作、设定控制参数为遗传算法的五大核心内容[9]。
BP神经网络用于预测间冷塔扇区出水温度,很容易陷入局部最小值;而且BP神经网络模型中,初始权重和阈值是随机的,容易出现网络振荡和不收敛的现象。遗传算法是一种通过全局搜索寻找最优解的方法,能有效地解决BP网络收敛速度慢且容易陷入局部极小值的问题,在BP神经网络模型中的应用主要是优化网络的初始权值和阈值[10-12]。理论上,优化后的BP神经网络模型具有较好的预测性能。遗传算法优化后的BP网络流程如图2所示。
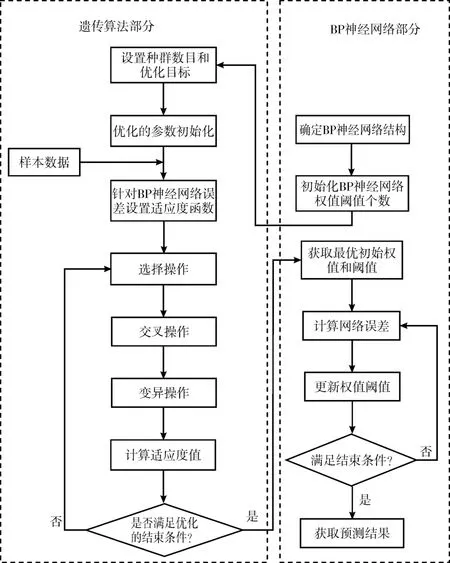
图2 GA -BP神经网络算法流程
在遗传算法中,首先要对遗传算法的参数进行初始化。在该模型中,种群规模设为50、遗传代数设为200、交叉概率设为0.3、变异概率设为0.1。为了提高遗传算法的收敛速度和计算精度,对BP神经网络的连接权值Wij和阈值(θ1、θ2、...、θn)进行编码。遗传算法的具体计算步骤如下:
1)产生随机种群。根据BP神经网络的拓扑结构,输入层、隐含层和输出层的神经元数分别为R、S1和S2。可根据式(1)确定群体的个体编码长度S为301。
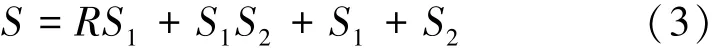
2)判断种群个体适应度是否符合优化准则,如果符合,则输出最佳个体及最优解,如果不符合,则进入下一步。通过编码来获得网络的初始值,将模型训练的预估值与期望值之间的误差当作适应度函数,计算公式为:
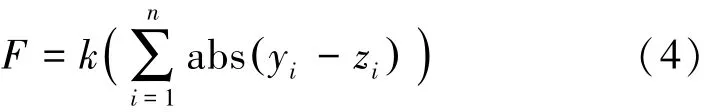
式中,n为输出节点数;yi为BP神经网络第i个节点的期望输出;zi为BP神经网络第i个节点的预测输出;k为常数。
3)根据适应度进行选择父母,适应度高的个体被选中的概率大,适应度低的个体被淘汰。染色体编码的基因选择概率px为:
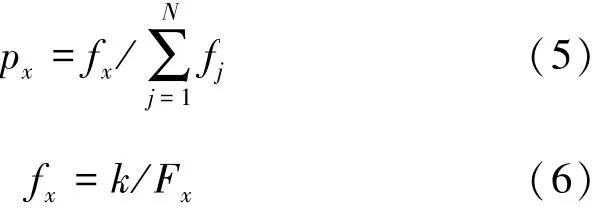
式中,Fx为个体x的适应度值;N为个体种群数;k为常数。
4)同父母的染色体按照一定的方法进行交叉,生成子代。第k条染色体ak与第l条染色体al在j处交叉的操作方法如下:
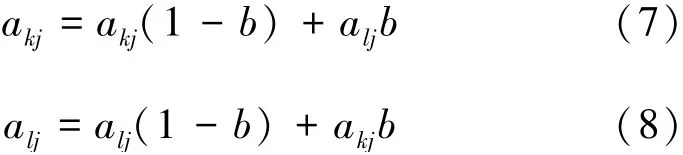
式中,b为0~1之间的随机数。
5)对子代染色体进行变异。选择第i个个体aij的第j个基因进行变异,变异操作方法如下:
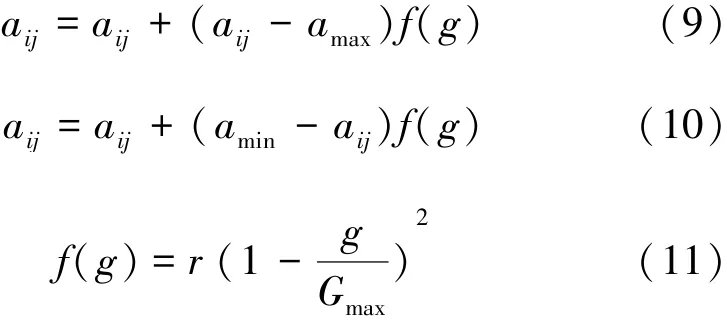
式中,r为0~1之间的随机数;g为当前的迭代次数;Gmax为最大的进化次数,取值为10。
2.3 PSO-BP神经网络
粒子群优化算法(PSO)类似于遗传算法,也是一种基于迭代的优化算法,基本思想是受鸟类群体行为建模与仿真研究结果的启发[13],但不存在交叉、变异等操作。与遗传算法相比,该算法参数少,原理简单,易于实现,搜索过程是通过粒子不断更新自己的速度和在解空间中的位置,以跟踪最优粒子。PSO-BP神经网络中的粒子特征主要由三个因素表征:粒子的位置、速度和适应度值。通过寻找个体最佳和群体最佳位置来获取最佳初始权值和阈值,并将其赋予给BP神经网络,在某种程度上,避免了传统BP神经网络采用误差反向传播网络连接权重调整,不容易陷入局部最优解,提高BP神经网络预测精度[14-15]。
PSO-BP神经网络模型是将BP神经网络各层的初始权值和阈值映射为PSO算法中粒子的位置向量,以BP神经网络训练数据预测误差绝对值之和作为适应度函数,当适应度值达到设定精度或者迭代达到设定的次数时迭代终止,从而得到最优的初始权值和阈值[16-17]。算法流程如图3所示。
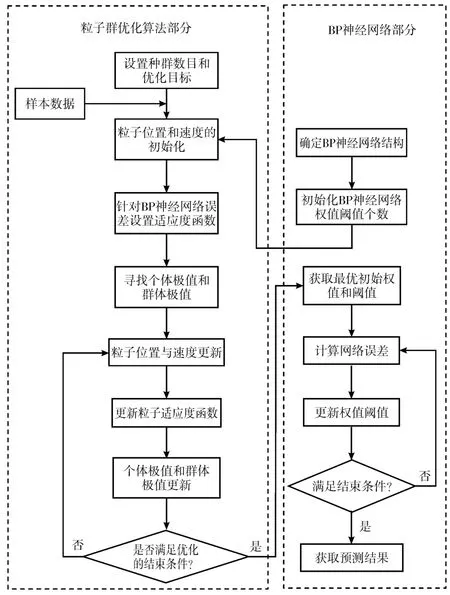
图3 PSO-BP神经网络算法流程图
在N维搜索空间中,PSO算法首先随机初始化一个粒子群,得到第i个粒子的位置和速度。然后,根据公式(4)确定每个粒子的适应度值F。对于每个粒子,将其适应度值与已经获得的最佳位置pbest进行比较,如果pbest更好,则用更好的pbest代替。同时,还将其适应度值与该粒子群中已经获得的最佳位置gbest进行比较,如果gbest较好,则将gbest替换为更好的位置。在每次迭代中,每个粒子找到的最优解为pbest,而整个种群找到的最优解为gbest。每个粒子都通过这两个最优解来更新它的速度和位置。在PSO中,通过式(12)和式(13)更新每个粒子的速度和位置。
速度更新公式为:
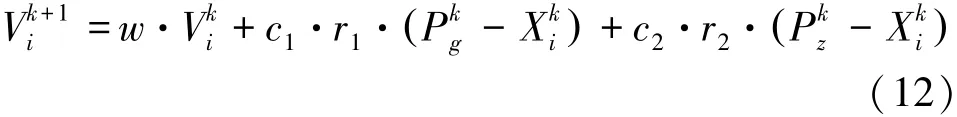
位置更新公式为:

式中,k为当前迭代次数;指种群中第i个粒子第k+1代移动速度;指种群中第i个粒子第k代移动速度;pbest和gbest分别为已获得的最佳适应度值;w为惯性权重;r1和r2为0~1之间的随机数;c1和c2是粒子的加速因子,取非负常数。
粒子进化过程中惯性权重为:
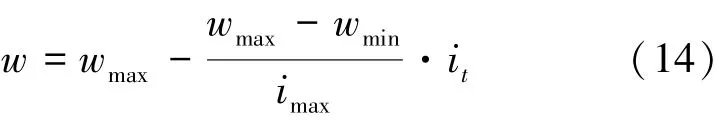
式中,imax指粒子群最大迭代次数;it指粒子当前迭代次数;wmax为最大惯性权重;wmin为最小惯性权重。
将PSO算法计算的最优权值和阈值赋予BP网络,用于网络输出的样本训练和验证结果。PSOBP神经网络结构为28-10-1,所需要的PSO模型参数设置如下:种群规模为50,进化次数为200,粒子个数为5,加速因子c1=c2=1.494 45;粒子的位置间隔为[-5,5],速度间隔为[-1,l]。
3 结果分析
3.1 预测值与实测值对比分析
图4、图5和图6分别给出了BP神经网络模型、GA-BP神经网络模型和PSO-BP神经网络模型的预测值与实测值的对比曲线图。由图4可以看出,BP神经网络模型的预测值与实测值变化趋势一致;由图5和图6可以看出,GA-BP神经网络模型和PSO-BP神经网络模型的预测值与实测值都非常接近,但GA-BP、PSO-BP神经网络模型的预测结果明显优于BP神经网络模型的预测结果。
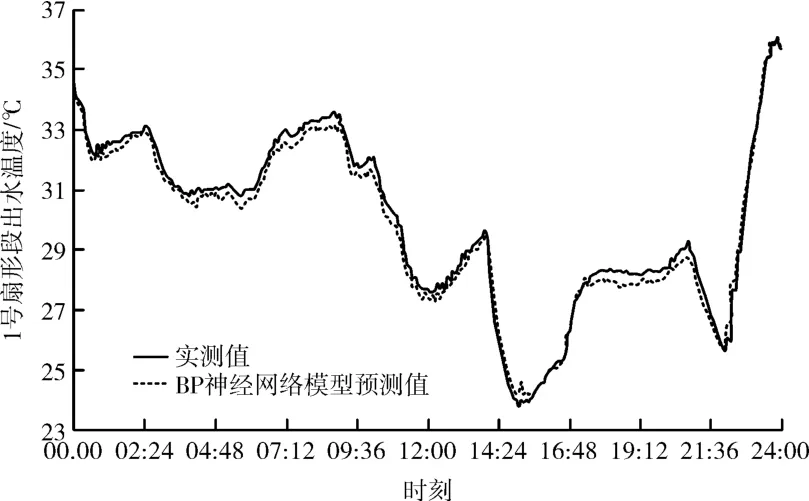
图4 BP神经网络模型预测值与实测值的对比曲线
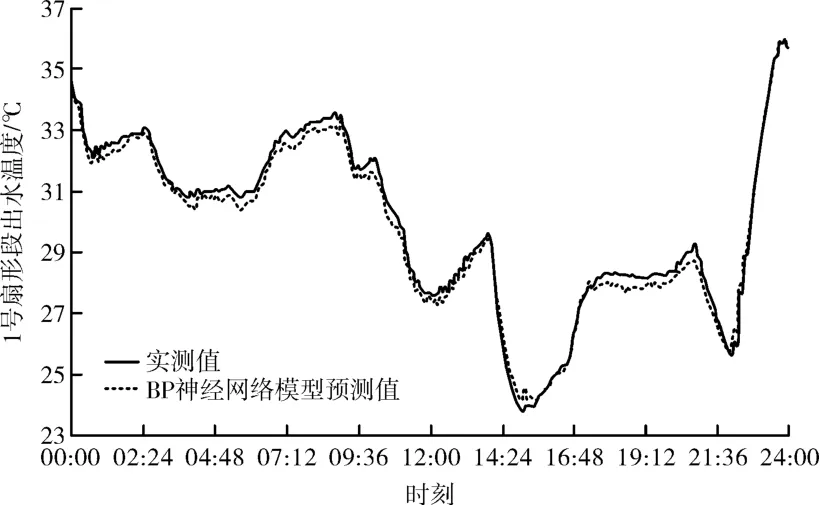
图5 GA-BP神经网络模型预测值与实测值的对比曲线
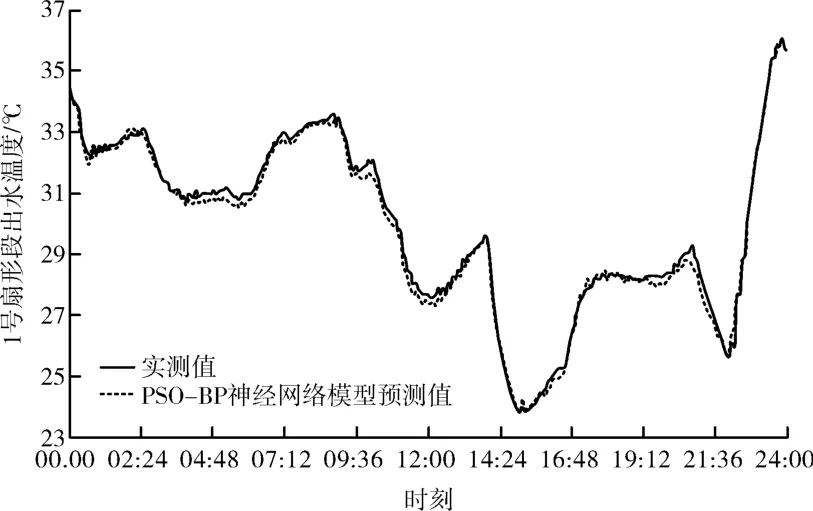
图6 PSO-BP神经网络模型预测值与实测值的对比曲线
3.2 误差对比分析
为更加清晰地展示三种神经网络模型的预测精度对比结果,通过平均绝对误差(εMAE)、平均绝对百分比误差(εMAPE)对三种神经网络模型的预测误差进行评价,两个指标的表达式如式(15)和(16)所示。
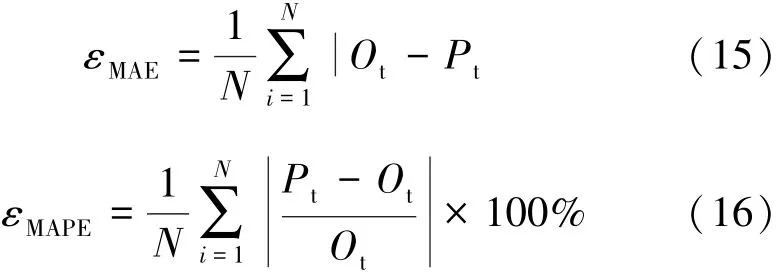
式中,N为预测扇区出水温度的数据点个数;Pt为模型预测值;Ot为实测值。
误差统计结果则见表2。可以看出,GA-BP和PSO-BP神经网络模型的的预测结果误差要明显小于单纯的BP神经网络模型,说明两种优化算法均能实现对BP神经网络的初始参数的优化。GA-BP的平均绝对误差(εMAE)为0.1855,平均绝对百分比误差(εMAPE)为0.62%。PSO-BP的平均绝对误差(εMAE)为0.1725,平均绝对百分比误差(εMAPE)为0.58%。PSO-BP神经网路模型的预测精度要略高于GA-BP神经网络模型的预测精度。
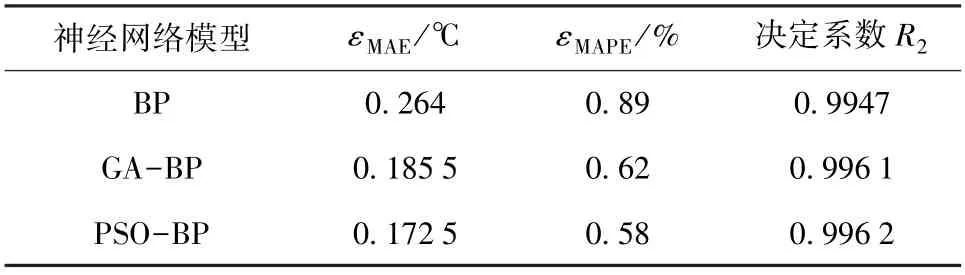
表2 三种神经网络模型的预测误差对比
三种神经网络模型的预测误差结果对比如图7所示。BP神经网络模型的预测误差曲线波动较大,最大值为-2.414%,GA-BP神经网络模型的预测误差最大值为-2.281%,PSO-BP神经网络模型的预测误差最大值为-2.077%。PSO-BP神经网络模型的误差曲线整体趋势更加接近误差零,性能较好。因此,PSO-BP神经网络模型能更为准确地对间冷塔扇区出水温度进行预测。
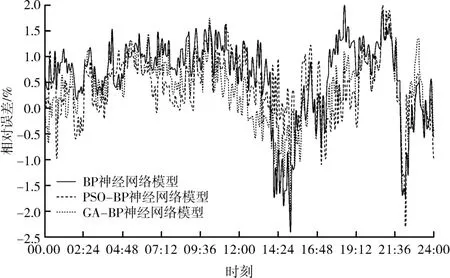
图7 三种神经网络模型预测相对误差对比
4 结语
通过对某330 MW机组DCS采集的数据进行灰色关联分析,得到间冷塔扇区出水温度与冷却塔进水温度、扇形段冷却柱表面温度、旁路阀差压、环境温度、扇形段百叶窗开度等因素之间的关联度密切。从扇区出水温度的预测结果可以看出,通过粒子群优化算法和遗传算法对BP神经网络的初始权值和阈值进行优化,均达到了提高BP神经网络模型预测精度的效果,且PSO-BP模型比GA-BP模型的预测精度更高。PSO-BP模型预测的平均绝对误差(εMAE)为0.172 5,平均绝对百分比误差(εMAPE)为0.58%,预测误差最大值为-2.077%。PSO-BP神经网络模型能更为准确地对间冷塔扇区出水温度进行预测,可指导间冷塔扇区的散热效果评价,使散热器在冬季低温工况下,扇区出水温度在最低允许温度之上,有效预防扇区结冻,也为散热器冷却柱结冻故障预警及诊断提供有效的判断依据,进一步保证间接空冷机组冬季工况下运行的安全性。
