瞬态热冲击下热电材料梁的温度场及热应力分析

滕兆春, 杨文秀

(兰州理工大学 理学院, 甘肃 兰州 730050)

随着人类社会的发展和科学技术的进步，能源环境问题已成为当前最紧迫的问题之一.越来越多的科学研究者们更倾向于寻求研发高性能、低污染、清洁型对环境友好的新型材料，而热电技术的出现实现了对这一理念的创新突破.这是一个通过转换利用太阳热能、回收工业部门和汽车尾气中废热的一项具有开创性、前瞻性的高新技术[1].而这种创新型技术最本质的参数是Seebeck系数s，在将系统内的温差直接转换为电压方面起着不可或缺的作用，一个高性能的热电材料同时还应保证具有高的电导率γ，低的热导率κ，通常用热电系数值Z=s2γ/κ来描述.热电材料就是近年来科学研究者不断挖掘不断完善的新型清洁材料，高性能热电材料就是热电技术的核心，人们习惯用热电性能指数ZT的大小来衡量热电材料性能的高低.按工作温度可分为高温(≥700 ℃)、中温(400～700 ℃)和低温(30～400 ℃)热电材料，在室温附近的Bi-Te化合物是目前公认的最好的热电材料，也是研究最多、最为成熟的，它广泛用于热电制冷元件；高温区的Si-Ge化合物大多用于航天设备的温差发电系统.

在近60年的历史中，热电材料研究领域几经停滞，但每一次都会以新的方式复兴[2].Riffat等[3]发现热电材料制成的小型热电器件它们是可靠的能量转换器，具有体积小、重量轻、无传动部件、无噪声运动等优点特点，因为没有机械运动部件，降低了噪音和振动的产生，进而可以将其用于工程中，用来减小或消除响应带来的对机械的损耗.虽然热电材料是一种面对能源和环境问题最佳的选择，但是由于在材料的制备过程中或多或少存在操作误差或机器设备不够精密，所制备的材料会存在含有杂质、裂纹等问题，科学研究者们对存在的该类问题进行了大量的分析.Wang等[4-5]分析了含椭圆夹杂的热电材料板的二维、三维问题，发现最大热电场集中总是出现在与加载方向垂直的椭圆轴的端点，且在夹杂物周围的热不透硬夹杂物会发生最大的应力集中.Wang等[6]分析了由绝缘层隔开的n型和p型热电偶组成的多层热电材料(TEM)中的瞬态层间应力，和绝缘层厚度和材料性能对剥离应力的影响.研究发现，总体上瞬态时的层间应力水平高于稳态时的层间应力水平.Song等[7]在研究热电材料板裂纹的二维问题发现，裂纹尖端的热流场、电流场和应力场均表现出传统的平方根奇异性.Al-Merbati等[8]通过商业软件ABAQUS对热电发电机进行热力学和热应力分析时发现，在一定的几何结构下，器件的热效率会有所提高，且在这种情况下，管脚中产生的最大热应力略有降低，这对设备的预期寿命会有所提高.Jin[9-10]利用层合复合材料的热弹性理论，研究了多层薄膜热电材料结构中的热应力和变形以及屈曲，发现用层合板模型计算的热应力比用材料强度模型预测的热应力要大得多.Gao等[11]利用ANSYS软件中的有限元分析模型，根据热电材料的各向异性力学性能和热电性能，给出了透射电镜的热应力分布.

到目前为止，热电材料已成功应用于人造卫星、太空飞船等高性能接收器及传感器等领域[12].这是一种不需要繁琐复杂的附加条件就可以直接将热能转化为电能的环境友好型能源材料，从而可以将其大规模地应用于发电和取代现有的氟利昂制冷机，为解决能源问题开辟了新的途径，同时也可缓解环境污染等问题[13].因为它具有这些突出的优点，许多国家都对热电材料技术给予了充分的重视并给与大力支持.对高性能热电材料不管是从材料学还是力学方面进行分析，都是近期的一个新研究热点，且在热电薄膜和热电板的热应力及其断裂力学等研究方面也取得了有价值的成果，但是研究的范围还很受局限，目前对热电材料梁力学性能的分析在国内外还未见有相关文献报道.

作为热电材料的基本结构之一，热电材料梁在实际热电工程中具有重要应用.因此本文将Wang等[14]给出的热电耦合控制方程拓展应用到热电材料梁，基于热电材料梁的一维瞬态控制方程和热应力分析理论，着重研究了两种类型Bi2Te3热电材料在不同时刻沿厚度方向温度和热应力的变化及最值出现的区域.由此为热电材料梁在受到热冲击时对热应力的分析提供了必要的数值分析和理论依据，这对热电材料梁工程安全性评估和后续力学行为的研究提供一个有力的支撑.

1 瞬态热电场控制方程的建立

1.1 热电平衡方程

根据热电材料系统内部的电荷和能量守恒以及热能和电能相互转换关系可得出热电材料的平衡方程.考虑热电材料各向同性，电和热沿电势和温度梯度的方向流动[14]，并忽略系统内的电或磁的瞬态效应干扰.设Ω表示以闭合曲面Γ为界的区域内的体积，dS为曲面微分元，n为向外的法向量，dx为Ω中的体积微元.根据散度定理[5,15]和高级微积分可知下列关系式成立：

(1)

式中：j为电流密度.式(1)可以改写为

-∇·j=-ji,i=0

(2)

式中：i为求和下标i=1,2,3.式(2)为第一个热电平衡方程.

热电材料的固有属性是在系统内发生热能Q1与电能Q2的相互转换，根据能量守恒定律和瞬态响应特性，即

Q1+Q2=CvT,t

(3)

其中热能和电能分别为

(4)

式中：Cv=ρc代表体积比热,J/(m3·℃),ρ为材料质量密度，c为比热；q为热流密度矢量；V和T分别为电势和温度；t为时间.则式(3)可简化为

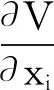
(5)

式(5)为第二个热电平衡方程.

1.2 热电本构方程

热电材料的系统内温度发生变化，就会产生电势梯度，从而发生热与电的相互转换，该现象为塞贝克效应：

(6)

式中：φi为电势梯度,V/m;s为Seebeck系数.当热电材料系统内温度恒定时存在欧姆定律

(7)

式中：γ为电导率.将式(6)与式(7)叠加即可得第一个热电本构方程[5,14,16]：

(8)

当热电材料内无电流产生时，傅里叶定律成立：

(9)

式中：κ为热导率.

热电材料系统内的机理很是复杂，其中帕尔贴效应与汤姆逊效应的深层机理[15]为

q=Te=sTj

(10)

式中：e为熵,J/℃.再将式(9)与式(10)叠加即可得第二个热电本构方程:

(11)

将式(2)和式(8)代入式(5)结合式(11)可得瞬态热冲击下热和电耦合的控制方程

(12)

2 热电材料梁力学计算模型

2.1 热冲击下热电材料梁温度场的建立

建立模型如图1所示的长×宽×高为L×b×h的两端固定的矩形截面热电材料梁.受到热冲击后的热电材料梁系统内的温度为只关于z坐标的一维温度场，该温度场可以表示为T=T(z,t).在上表面h/2处受到热冲击后系统产生温度变化，在t=0时刻，热电材料梁系统温度为T0(T0为系统的参考温度)；t>0时，梁两侧的温度突然改变至T(h/2,t)=Ta、T(-h/2,t)=Tb.

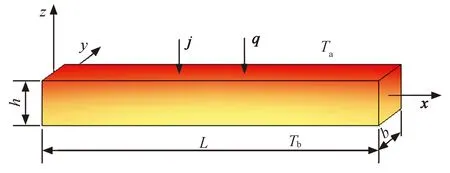
图1 热电材料梁计算模型

将式(12)的控制方程改写为只关于z坐标的一维热冲击控制方程如下：

(13)

式(13)可看作是由稳态项与瞬态项的和，为了方便求解可引入辅助函数，令

T(z,t)=U(z,t)+W(z)

(14)

式中：W(z)和U(z,t)代表温度场所满足的稳态项和瞬态项，将式(14)代入式(13)，式(13)可改写为

(15)

将式(15)简化为关于W(z)和U(z,t)的两方程如下：

(16)

(17)

式(16)为二阶常微分方程，利用边界条件积分得

(18)

得出瞬态温度场T(z,t)的稳态项W(z)的函数.

式(17)为热传导方程，故采用分离变量法求解.令

U(z,t)=Z(z)T(t)

(19)

代入式(17)得

κZ″T=CvZT′

(20)

即

(21)

等号左边为关于z的函数，右边为关于t的函数，要使等式成立，等式两边只能为一常数，令其参数为-λ，则式(21)化为以下两微分方程：

利用边界条件求解式(22)得其特征值为λn，其值为

则对应的特征函数为

(24)

式中：Cn为任意常数.

将λn代入常微分方程(23)得

n=1,2,3,…

(25)

式中：Dn为任意常数.

(26)

式中：Cn是由式(24)的Cn和式(25)的Dn并入组合成新的常数.对式(26)再叠加求和得

(27)

式中：n=1,2,3,…，得出瞬态温度场T(z,t)的瞬态项U(z,t)的函数.

将初始条件Uz,0=T0-Wz代入式(27)，可得

n=1,2,3,…

(28)

式中:Cn可利用傅里叶三角级数表示如下:

将式(18)和式(27)代入式(14)可得瞬态温度场的完整表达式

n=1,2,3,…

(29)

2.2 瞬态热冲击下热电材料梁热应力场的建立

热电材料梁受热冲击作用时，梁内各点将会产生温度的变化，从而导致梁出现膨胀或收缩变形，若外部约束使膨胀或收缩变形不能自由发生时，在热电材料梁结构中就会出现热应力.近代线性热应力理论创始于1835年，由法国人J.M.C.杜哈梅尔初次提出，随后在1841年，德国人诺曼伊曼初次导出线性热应力理论，他们两者提出的理论基本相同，故将现代的线性热应力理论称为杜哈梅尔—诺伊曼理论[17].

根据热应力理论，在自由状态下，梁在热环境中的轴向自由伸长量为

Δl=αΔTl

(30)

式中：α表示热电材料的热膨胀系数;ΔT表示温度的变化,ΔT(z,t)=T(z,t)-T0.轴向自由伸长线应变为

εxxz,t=αΔT(z,t)

(31)

则得到热电材料梁内热应力与温度变化的关系为

(32)

式中：E为热电材料的弹性模量.

3 计算结果与分析

3.1 p型Bi2Te3热电材料梁温度场及热应力场

Bi2Te3合金在熔点温度时的化合物组分中富含Bi原子，过剩的Bi原子在晶格中占据了Te原子的位置后形成p型Bi2Te3热电材料；反之，过剩的Te原子在晶格中占据了Bi原子的位置，则形成n型Bi2Te3热电材料.一般规定n型半导体热电材料的seebeck系数取负值，p型半导体热电材料的seebeck系数取正值[18].Bi2Te3热电材料其它相关物理参数结合文献[19]和文献[20]，见表1.

表1 两种类型Bi2Te3热电材料相关物理参数

热电材料梁的几何参数为L=0.1 m、h=0.004 m、b=0.003 m，初始参考温度为T0=25 ℃，受到热载荷冲击后梁上表面温度变为Ta=240 ℃、下表面温度变为Tb=30 ℃，由于在方程(2)中-ji,i=0可以得出电流密度j为一常数，取j0=3.199×106A/m2[15].

通过MATLAB对温度场和热应力场解析函数的编程计算发现温度场和热应力场沿厚度z方向的特性曲线呈抛物线分布.梁产生热应力场主要是因为受到热冲击时热电材料梁系统内存在温度梯度，使梁受热不均匀导致.对图2和图3温度场和热应力场特性曲线分析发现，在达到稳态前梁的中性层以下的温度呈陡坡式的剧增，进而所对应的热应力也出现剧增；但是时间的增加温度和热应力随厚度z方向的增加趋于缓慢，且随时间的增加温度小幅度向受热冲击前回转，逐渐趋于稳态化后均不再随时间变化；在梁的中性层以上：温度场沿厚度z方向总体呈现缓慢下坡式的递减最终达到与梁上层温度一致，但是随时间的增加温度和热应力出现小幅度的增加这与中性层以下的变化恰好相反.导致这种变化的原因是因为图4表示的温度场的瞬态项特性曲线是以三角函数的变化出现有正有负，且随时间的增加温度场瞬态项变化曲线走势变的舒缓最终不再随时间变化，进而影响了不同时刻下瞬态温度场和热应力整体的变化趋势.以中性层为分界线，分界线两侧呈现不同的变化趋势，热应力沿梁厚度方向z出现增加、减小最终趋于稳定.热电材料梁在达到稳态前最大热应力发生在中性层附近，在达到稳态后最大热应力向高温区移动，证明在稳态下梁的最大热应力发生高温区，并且达到稳态后的热应力最值大于瞬态时的热应力最值，这与热环境下梁的应力分析相符.

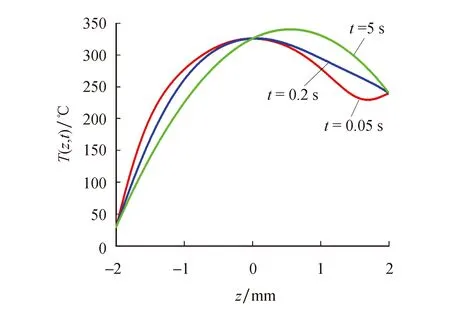
图2 不同时刻温度沿p型Bi2Te3热电材料梁截面厚度方向的变化曲线 (T0=25 ℃)

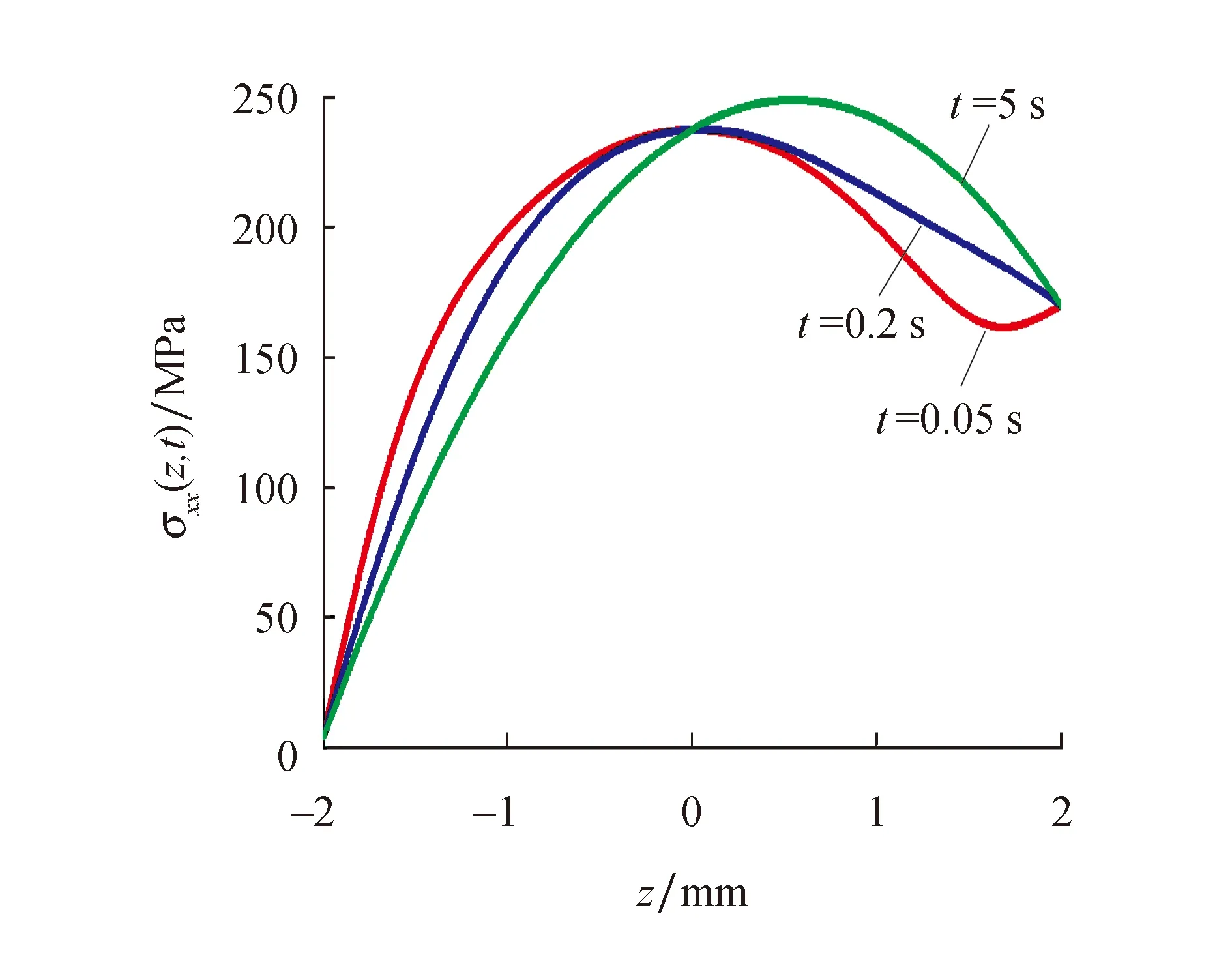
图3 不同时刻热应力沿p型Bi2Te3热电材料梁截面厚度的变化曲线

图4 不同时刻p型Bi2Te3热电材料梁温度场中的瞬态项沿截面厚度方向的变化曲线

3.2 p型和n型Bi2Te3热电材料梁温度场和热应力场的对比分析

在t=5 s时温度场已达到稳态不再随时间变化，在相同温度区间内不同型的热电材料物理参数不同，则材料的性能也不同.从图5两种热电材料梁温度场特性曲线发现p型Bi2Te3热电材料梁系统内温度大于n型Bi2Te3热电材料梁系统内温度，n型Bi2Te3热电材料梁的温度场变化比p型Bi2Te3热电材料梁的较为缓慢.从图6三个不同时间下的p型和n型Bi2Te3热电材料梁热应力具体特性曲线变化图可以直观得到，n型Bi2Te3热电材料梁的热应力小于p型Bi2Te3热电材料的热应力，n型热电材料热应力比p型热电材料热应力变化缓慢，不会出现剧增剧减的现象.根据n型、p型热电材料梁温度和热应力变化的特征，如果将其应用于制作热电器件的电偶，可以得出当电流从n型材料传递到p型材料时为冷却效应，当电流从p型材料传递到n型材料时为加热效应，这与帕尔贴效应得出的结论是一致的.

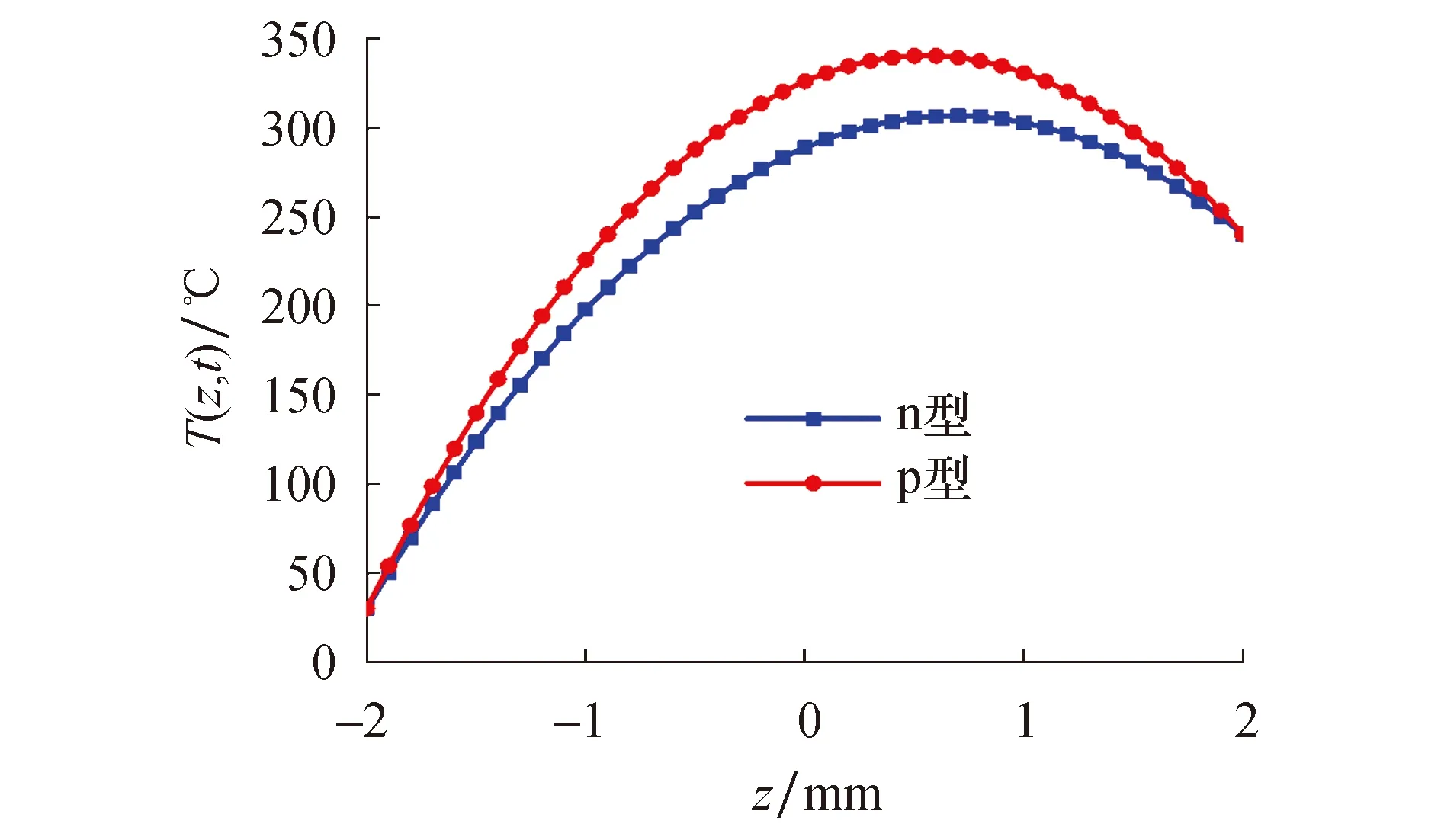
图5 p型和n型Bi2Te3热电材料梁温度沿截面厚度的变化曲线(T0=25 ℃、t=5 s)

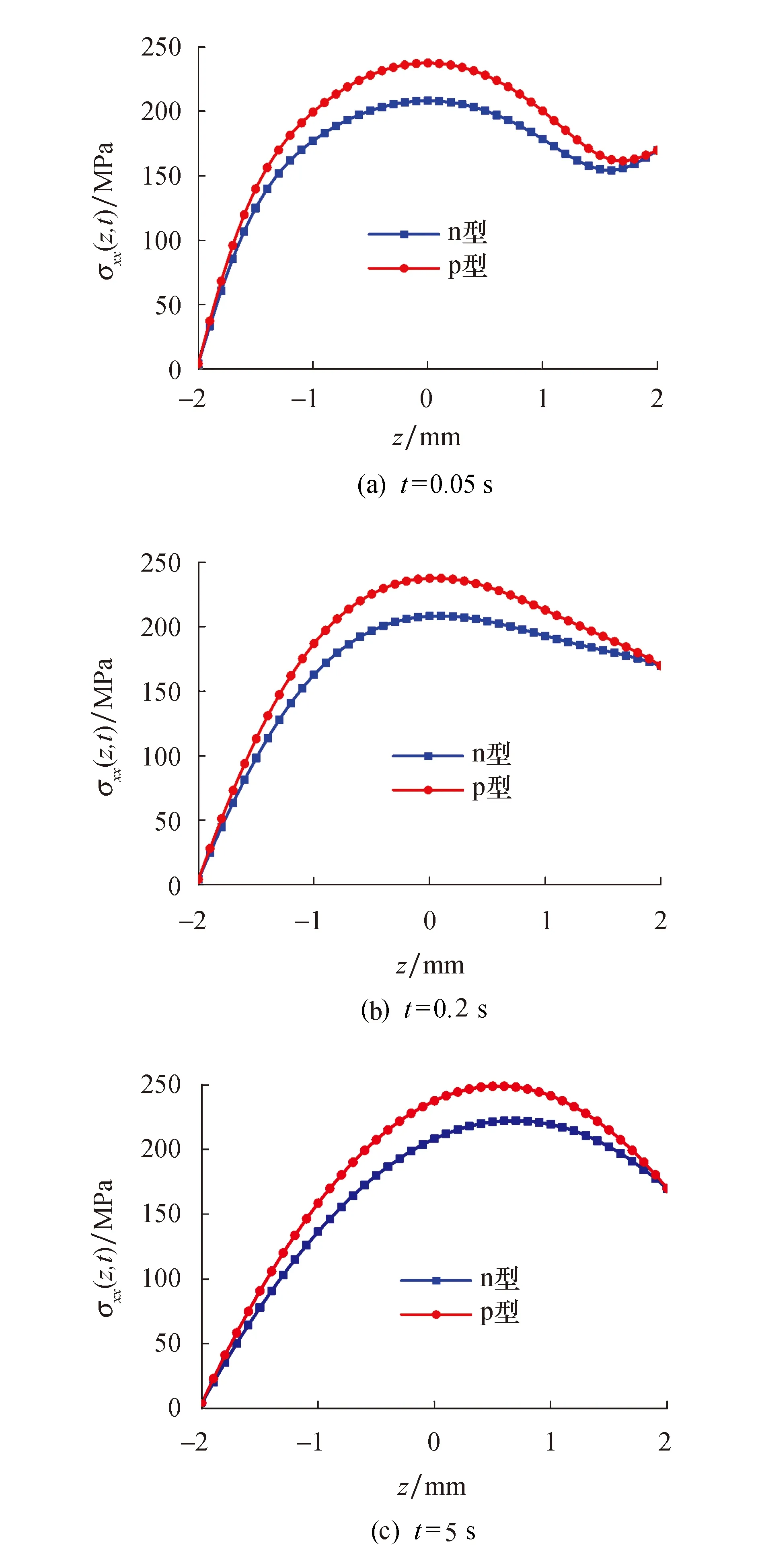
图6 不同时刻p型和n型Bi2Te3热电材料梁的热应力沿厚的变化曲线

4 结论

本文基于瞬态热冲击下热电材料的控制方程，采用分离变量法推导出的热电材料梁瞬态温度场，并结合梁的热应力分析理论得出瞬态热应力场的解析函数表达式，利用数学软件MATLAB求解出相应的特性曲线，得出如下结论：

1) Bi2Te3热电材料梁在电流密度为j0=3.199×106A/m2时温度场随厚度方向z的函数变化呈抛物线分布，因受温度场瞬态项的正负变化，导致温度场随梁厚度的变化出现有增有减的现象.

2) 在达到稳态后热应力不再受时间的影响，并且最大热应力向高温区移动，稳态下的最大热应力大于瞬态下的最大热应力.

3) p型Bi2Te3热电材料梁的热应力比n型热电材料产生的热应力大，说明n型Bi2Te3热电材料梁在受到热冲击后的力学性能要比p型Bi2Te3热电材料梁的力学性能更好.不易在受到热冲击短期内由于热应力对材料力学性能的影响而快速进入疲劳期，导致结构受损，从而影响热电材料梁的使用寿命.