有限非链环上几类常循环码构造量子码
2022-01-04朱娅婷朱士信
朱娅婷,朱士信
(合肥工业大学 数学学院,安徽 合肥 230601)
自文献[1]提出量子码以来,量子码开始备受关注。量子计算具有很大的应用前景,为了更好地发挥它的作用,需要对其进行纠错。量子纠错是量子计算和量子通信得以实现的重要保证,而常循环码作为经典纠错码中重要的一环,在量子纠错方面具有重要作用。有限环上循环码的量子纠错码的构造受到广泛关注,而有限环上常循环码的量子纠错码的构造研究较少。本文研究环Fq+uFq+vFq+uvFq上的常循环码,并利用它们构造量子码。
文献[2]首先利用有限链环F2+uF2,u2=0上奇数长度的循环码构造了量子码;文献[3]利用有限链环F4+uF4,u2=0上奇数长度的循环码构造量子码;文献[4]用一种新的方法研究有限非链环F2+vF2,v2=v上任意长度的循环码,构造量子码;文献[5]利用有限非链环Fp+vFp,v2=v上循环码构造量子码;文献[6]通过Gray映射,利用环Fp+uFp,u2=1上u-常循环码构造量子码;文献[7]利用环F2+uF2+vF2+uvF2,u2=u,v2=v,uv=vu上循环码构造量子码;文献[8]利用环F3+uF3+vF3+uvF3,u2=1,v2=1,uv=vu上循环码构造量子码;文献[9]给出环Fq+uFq+vFq+uvFq上斜循环码的结构,其中u2=u,v2=v,uv=vu,p为奇素数,并利用此环上的循环码构造量子码。此后,环上线性码的量子码的构造受到越来越多的关注,基于各种不同环上的线性码,学者们构造了许多参数较好的量子码[10-12]。
本文研究环Fq+uFq+vFq+uvFq的性质结构,构造环Fq+uFq+vFq+uvFq到域Fq上一个新的保线性、保距、保自正交的Gray映射;证明环Fq+uFq+vFq+uvFq上16类常循环码可分解成不同类型的循环码和负循环码的组合,并利用其构造量子码;最后与已知的量子码比较,本文构造的量子码具有更好的参数。
1 基础知识
设m为正整数,p是奇素数且p≠3,q=pm,Fq是含有q个元素的有限域。设
R=Fq+uFq+vFq+uvFq,
u2=u,v2=v,uv=vu,
则R是一个交换的主理想环,它是含有4个极大理想的半局部环。令θ1=uv,θ2=u-uv,θ3=v-uv,θ4=1-u-v+uv,易证,θ1、θ2、θ3、θ4是环R的一组本原幂等元。
由文献[9]可得:
R=θ1R⨁θ2R⨁θ3R⨁θ4R,
θiR≅Fq,i=1,2,3,4。
由中国剩余定理得:
R=θ1Fq⨁θ2Fq⨁θ3Fq⨁θ4Fq,
其中,⨁表示直和。环R中任意元素r可以唯一表示为:
r=θ1r1+θ2r2+θ3r3+θ4r4,
r1、r2、r3、r4∈Fq。
设Rn表示环R上n-元组全体构成的R模。Rn中每个n-元组c可以唯一表示为:
c=θ1c1+θ2c2+θ3c3+θ4c4,

Rn的每一个非空子集C称为环R上长度为n的码,码C中的元素称为码字。若C是Rn的R-子模,则称C为R上长度为n的线性码。
设λ是环R的单位,码C是环R上长度为n的线性码。若对任意的(c0,c1,…,cn-1)∈C,有
(λcn-1,c0,…,cn-2)∈C,
则称C是环R上长度为n的λ-常循环码。
特别地,当λ=1时,C为循环码;当λ=-1时,C为负循环码。
设a=(a1,a2,…,an),b=(b1,b2,…,bn)是Rn中任意2个元素,则它们的内积定义为:
a·b=a1b1+a2b2+…+anbn。
若a·b=0,则称a和b是正交的。环R上码长为n的线性码C的对偶码定义为:
C⊥={a∈Rn|a·b=0,∀b∈C}。
若C⊆C⊥,则称C是环R上长度为n的自正交码。
设C是环R上长度为n的线性码,定义
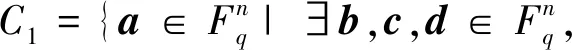
θ1a+θ2b+θ3c+θ4d∈C},
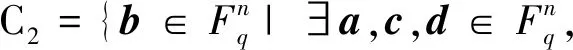
θ1a+θ2b+θ3c+θ4d∈C},

θ1a+θ2b+θ3c+θ4d∈C},
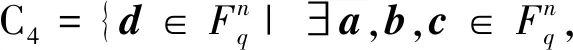
θ1a+θ2b+θ3c+θ4d∈C}。
显然,Ci是Fq上长度为n的线性码,且
C=θ1C1⨁θ2C2⨁θ3C3⨁θ4C4,
|C|=|C1||C2||C3||C4|。
设G是环R上一个n×m矩阵。若线性码C的任意一个码字都可以表示成G中行n元组的线性组合,且G中行n元组线性无关,则称G为码C的生成矩阵。若可以通过坐标置换,从一个码得到另一个码,则这2个码是等价的。设Ci的生成矩阵为Gi,则C和φ(C)的生成矩阵分别为:G=[θ1G1θ2G2θ3G3θ4G4]T且φ(G)=[φ(θ1G1)φ(θ2G2)φ(θ3G3)φ(θ4G4)]T。
2 Gray映射
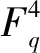
θ1r1+θ2r2+θ3r3+θ4r4|→
其中,r1、r、r3、r4∈Fq。
命题1 当p≠3时,φ是一个双射。
证明对任意r=θ1r1+θ2r2+θ3r3+θ4r4和r′=θ1r1′+θ2r2′+θ3r3′+θ4r4′∈R,其中ri、ri′∈Fq,i=1,2,3,4,设φ(r)=φ(r′),则
解得:3r1=3r1′,3r2=3r2′,3r3=3r3′,3r4=3r4′。
因为p≠3,所以3在环R的单位。于是r1=r1′,r2=r2′,r3=r3′,r4=r4′,即r=r′。
因此φ为单射。

对码字c=(c1,c2,…,cn)∈C,汉明重量wtH(c)定义为c中非零元的个数。码C中2个码字x=(x1,x2,…,xn)和y=(y1,y2,…,yn)的汉明距离dH(x,y)=wtH(x-y)。码C中不同码字的汉明距离的最小值称为码C的极小距离,记作dH(C),即
dH(C)=min{dH(x,y)|x,y∈C,x≠y}。
当C是线性码时,
dH(C)=min{wtH(x)|x∈C,x≠0}。
对任意r∈R它的Gray重量定义为:
wtG(r)=wtH(φ(r))。
环R上的Gray映射可推广到Rn上,定义
a=(a1,a2,…,an)|→
(φ(a1),φ(a2),…,φ(an))。

对∀a,b∈Rn,a和b的Gray距离定义为:

证明对m、l∈Fq及∀a=(a1,a2,…,an)、b=(b1,b2,…,bn)∈Rn,有
φ(ma+lb)=
(φ(ma1+lb1),φ(ma2+lb2),…,φ(man+lbn))。
容易验证,φ是环R上的Fq线性映射,即
φ(mai+lbi)=mφ(ai)+lφ(bi)
对任意1≤i≤n成立。于是,
φ(ma+lb)=
(φ(ma1+lb1),φ(ma2+lb2),…,φ(man+lbn))=
(mφ(a1)+lφ(b1),mφ(a2)+lφ(b2),…,
mφ(an)+lφ(bn))=mφ(a)+lφ(b),
因此φ是Fq线性的。
下证保距性。
dG(a,b)=wtG(a-b)=
综上所述,命题2得证。
由Gray映射φ的定义及性质可得如下命题。
命题3 设C是环R上长度为n的线性码且dG(C)=d,则φ(C)是一个参数为[4n,k,d]的q-元线性码,其中k=logq|C|。
命题4 设C是环R上长度为n的线性码。若C是自正交码,则φ(C)也是Fq上自正交码。
证明在码C中,任取2个码字:
a=θ1a1+θ2a2+θ3a3+θ4a4,
b=θ1b1+θ2b2+θ3b3+θ4b4,

a·b=θ1a1·b1+θ2a2·b2+
θ3a3·b3+θ4a4·b4=0。
由此推出,
a1·b1=a2·b2=a3·b3=a4·b4=0。
于是
φ(a)·φ(b)=
3(a1·b1+a2·b2+a3·b3+a4·b4)=0,
即φ(a)与φ(b)正交。
由a和b的任意性,命题4得证。
命题5 设C=θ1C1⨁θ2C2⨁θ3C3⨁θ4C4是环R上长度为n的线性码,其中Ci是Fq上长度为n的线性码,则
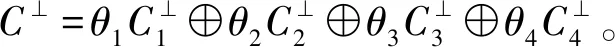
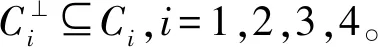

b·a=θ1b1·a1+θ2b2·a2+
θ3b3·a3+θ4b4·a4。
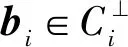
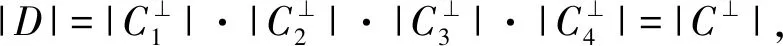
a=θ1a1+θ2a2+θ3a3+θ4a4∈C⊥。
因为C⊥⊆C,所以
θia=θiai∈θiC⊥⊆θiC=θiCi,
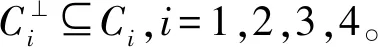
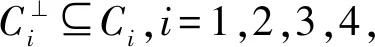
因此
θ1C1⨁θ2C2⨁θ3C3⨁θ4C4=C。
综上所述,命题5结论成立。
3 量子码的构造
本节主要研究环R上16类常循环码的分解情况,并利用其构造量子码,下面给出引理。
引理1[13](CSS构造)设C是Fq上参数为[n,k,d]的线性码。若C⊥⊆C,则存在参数为[[n,2k-n,≥d]]q的量子码。
为了基于环R上常循环码构造量子码,下面给出环R上常循环码的结构。
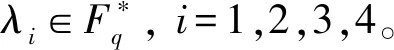
证明必要性。设ci=(ci,0,ci,1,…,ci,n-1)是Ci的任意一个码字,i=1,2,3,4,则
c=(c0,c1,…,cn-1)=θ1c1+
θ2c2+θ3c3+θ4c4∈C。
因为C是λ-常循环码,所以(λcn-1,c0,…,cn-2)∈C。
因为
λcn-1=λ(c1,n-1θ1+c2,n-1θ2+c3,n-1θ3+c4,n-1θ4)=
λ1c1,n-1θ1+λ2c2,n-1θ2+λ3c3,n-1θ3+λ4c4,n-1θ4,
所以对任意的1≤i≤4,有
(λici,n-1,ci,0,…,ci,n-2)∈Ci。
因此Ci是Fq上长度为n的λi-常循环码。
充分性。设a=(a0,a1,…,an-1)=θ1a1+θ2a2+θ3a3+θ4a4是码C的任意一个码字,其中
ai=(ai,0,ai,1,…,ai,n-1),i=1,2,3,4。
因为ai∈Ci且Ci是Fq上长度为n的λi-常循环码,所以ai′=(λiai,n-1,ai,0,…,ai,n-2)∈Ci。于是
(λan-1,a0,…,an-2)=
θ1a1′+θ2a2′+θ3a3′+θ4a4′∈C。
由a的任意性知,C是环R上长度为n的λ-常循环码。
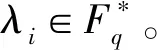
证明由定理1知,Ci是Fq上长度为n的λi-常循环码,因此存在gi(x)∈Fq[x]且gi(x)|(xn-λi),使得ci=(gi(x))。令
g(x)=θ1g1(x)+θ2g2(x)+θ3g3(x)+θ4g4(x)。
对任意c(x)∈(g(x)),存在
a(x)=θ1a1(x)+θ2a2(x)+
θ3a3(x)+θ4a4(x)∈R[x],
使得c(x)=a(x)g(x)。于是
c(x)=θ1a1(x)g1(x)+θ2a2(x)g2(x)+
θ3a3(x)g3(x)+θ4a4(x)g4(x)∈C。
因此(g(x))⊆C。
对任意c(x)∈C,存在ci(x)∈Ci,使得
c(x)=θ1c1(x)+θ2c2(x)+θ3c3(x)+θ4c4(x)。
因为ci(x)∈Ci,所以存在ai(x)∈Fq[x],使得ci(x)=ai(x)gi(x)。于是
c(x)=θ1a1(x)g1(x)+θ2a2(x)g2(x)+
θ3a3(x)g3(x)+θ4a4(x)g4(x)=
[θ1a1(x)+θ2a2(x)+θ3a3(x)+θ4a4(x)]×
[θ1g1(x)+θ2g2(x)+θ3g3(x)+θ4g4(x)],
即c(x)∈(g(x))。因此C⊆(g(x))。
综上所述,得C=(g(x))。
设hi(x)∈Fq[x],使得gihi(x)=xn-λi。令
h(x)=θ1h1(x)+θ2h2(x)+θ3h3(x)+θ4h4(x),
则h(x)∈R[x]且h(x)g(x)=θ1h1(x)g1(x)+θ2h2(x)g2(x)+θ3h3(x)g3(x)+θ4h4(x)g3(x)=θ1(xn-λ1)+θ2(xn-λ2)+θ3(xn-λ3)+θ4(xn-λ4)=xn-λ,因此g(x)|(xn-λ)。
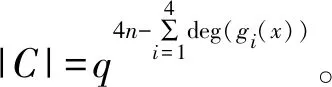
下面考察环R上长度为n的λ-常循环码C的对偶码C⊥的结构。由命题5得:
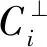
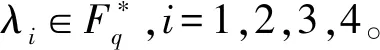
下面利用环R上长度为n的λ-常循环码C构造量子码。基于CSS构造码C需满足C⊥⊆C。因为C⊥是环R上长度为n的λ-1-常循环码,所以可以假设λ-1=λ,即λ2=1。
在环R上,方程x2=1有16个解,且解集为Λ={a1θ1+a2θ+a3θ3+a4θ4|a1,a2,a3,a4∈{1,-1}}。当λ∈Λ时,由命题5和定理1知,环R上长度为n的λ-常循环码可分解成Fq上长度为n的循环对偶包含码或负循环对偶包含码。

基于以上理论,关于环R上长度为n的λ-常循环对偶包含码有如下结论。
定理2 设λ=λ1θ1+λ2θ2+λ3θ3+λ4θ4,其中λi∈{1,-1},i=1,2,3,4。设C=θ1C1⨁θ2C2⨁θ3C3⨁θ4C4是环R上长度为n、生成多项式为g(x)=θ1g1(x)+θ2g2(x)+θ3g3(x)+θ4g4(x)的λ-常循环码,其中gi(x)∈Fq[x],且gi(x)|(xn-λi),则C⊥⊆C当且仅当
结合环R上长度为n的λ-常循环码的代数结构和对偶包含条件,可以构造如下参数的量子码。
定理3 设λ=λ1θ1+λ2θ2+λ3θ3+λ4θ4,其中λi∈{1,-1},i=1,2,3,4。设C=θ1C1⨁θ2C2⨁θ3C3⨁θ4C4是环R上长度为n、生成多项式为g(x)=θ1g1(x)+θ2g2(x)+θ3g3(x)+θ4g4(x)的λ-常循环码,其中gi(x)∈Fq[x],使得:
gi(x)|(xn-λi),
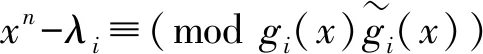
的量子码,其中dG是码C的最小Gray距离。
根据定理3,通过选取恰当的常循环码,得到一些新参数量子码。部分新参数的量子码与已知的量子码的参数比较,见表1所列。

表1 量子码的参数比较
例1 在F5[x]中,
x11-1=(x+4)(x5+2x4+4x3+x2+
x+4)(x5+4x4+4x3+x2+3x+4),
x11+1=(x+1)(x5+x4+4x3+4x2+
3x+1)(x5+3x4+4x3+4x2+x+1)。
设C是环R=F5+uF5+vF5+uvF5上码长为11、生成多项式为
g(x)=θ1(x5+x4+4x3+4x2+3x+1)+
θ2(x5+3x4+4x3+4x2+x+1)+
θ3(x5+2x4+4x3+x2+x+4)+
θ4(x5+4x4+4x3+x2+3x+4)
的(1-2u)-常循环码,其中
g1(x)=x5+x4+4x3+4x2+3x+1;
g2(x)=x5+3x4+4x3+4x2+x+1;
g3(x)=x5+2x4+4x3+x2+x+4;
g4(x)=x5+4x4+4x3+x2+3x+4。
容易验证,
由定理2知,C⊥⊆C。
由MAGMA计算知,φ(C)是F5上参数为[44,24,9]的线性码。由定理3知,存在参数为[[44,4,≥9]]的5元量子码。
文献[14]构造参数为[[44,4,≥7]]的量子码,因此本文构造的量子码具有更好的参数。
例2 在F11[x]中,
x20-1=(x+1)(x+2)(x+3)(x+4)×
(x+5)(x+6)(x+7)(x+8)×
(x+9)(x+10)(x2+1)(x2+2)×
(x2+3)(x2+4)(x2+5)(x2+9),
x20+1=(x2+x+6)(x2+2x+2)×
(x2+3x+10)(x2+4x+8)×
(x2+5x+7)(x2+6x+7)×
(x2+7x+8)(x2+8x+10)×
(x2+9x+2)(x2+10x+6)。
设C是环R=F11+uF11+vF11+uvF11上码长为20、生成多项式为
g(x)=θ1(x2+x+6)+
θ2(x2+2x+2)+θ3(x+2)+θ4(x+6)
的(1-2u)-常循环码,其中
g1(x)=x2+x+6;g2(x)=x2+2x+2;
g3(x)=x+2;g4(x)=x+6。
容易验证,
由定理2知,C⊥⊆C。
由MAGMA计算知,φ(C)是F11上参数为[80,74,3]的线性码。由定理3知,存在参数为[[80,68,≥3]]的11元量子码。
文献[16]构造参数为[[63,51,≥3]]的量子码,因此本文构造的量子码比文献[16]构造的量子码具有更大的码率。
4 结 论
本文研究环R=Fq+uFq+vFq+uvFq上的常循环码,引入一个新的保线性保距保自正交的Gray映射;基于环R的直和分解,研究该环上16类常循环码的分解,并利用其构造一些具有较好参数的量子码。本文进一步的工作是,选取其他类型的常循环码与Gray映射,构造参数更好的量子码。
