面向Kinect骨骼运动数据优化的堆叠双向循环自编码器

杨 晶,李书杰,刘晓平

(合肥工业大学 计算机与信息学院,安徽 合肥 230601)

人体骨骼运动数据在游戏设计[1-2]、影视制作、体育训练和医疗康复等领域得到了广泛的应用。人们可以通过高精度运动捕获系统,如Vicon光学运动捕捉系统和Xsens传感器运动捕捉系统等来获得人体骨骼运动数据,这些高精度运动数据采集设备获得的人体骨骼运动数据节点信息丰富并且精度较高,然而其价格昂贵且穿戴不便,难以普及使用。深度相机Kinect可以实时获取人体骨骼运动数据[3],其价格低廉、易于使用,但其获取的运动数据仅含25个骨骼节点并且含有大量的噪声。因此,通过Kinect获得的人体骨骼运动数据在实际应用之前需要经过优化处理。运动数据优化(motion refinement)包括2个方面:一方面是指补全运动数据中的缺失值;另一方面是去除运动数据中的噪声和异常值,并且优化后数据要能够保持运动数据的时空模式和人体运动学信息[4]。本文期望通过深度神经网络对Kinect数据进行优化,既能够补全Kinect缺失的骨骼节点信息也去除其中的噪声和异常值,提升Kinect骨骼运动数据的细节层次和数据精度,达到基于低精度便捷设备获取高精度动捕数据的目的。

近年来越来越多的学者采用深度学习的方法对运动数据进行优化处理并取得了较好的效果。例如,文献[5]利用基于卷积神经网络(convolutional neural network,CNN)的自编码器抽取运动数据流形,实现运动数据的去噪;文献[6]训练了一个基于双向长短时记忆(bidirectional long short term memory,Bi-LSTM)的滤波网络对噪声数据进行滤波处理;文献[7]提出一种基于Bi-LSTM的自编码器,并通过在训练时施加运动学约束提升去噪后数据的平滑自然性。但是这些方法对Kinect骨骼运动数据的优化仍存在骨骼扭曲等运动不自然的现象。本文借鉴计算机视觉领域用于从视频中提取人体骨骼运动数据的著名网络 ——“堆叠沙漏”(stacked hourglass)网络模型[8],该模型通过反复自下而上、自上而下的映射以及中间约束，有效地提升了运动姿态的估计效果。在运动数据处理领域,文献[5]指出运动数据到隐变量空间再到运动数据这一映射过程可以获得平滑自然的运动。在计算机视觉领域隐变量约束常被用来提高网络生成图像的感知真实性[9]。因此,本文提出一种面向Kinect运动数据优化的堆叠自编码器,将6个双向循环自编码器(bidirectional recurrent autoencoder,BRA)进行堆叠,使得噪声数据能够多次重复从运动数据到隐变量空间再到运动数据这一映射过程,并且同时使用隐变量约束提升优化后数据与动捕数据之间的感知相似度,使得网络生成的运动真实自然。

综上所述,本文主要工作包括以下3点:

(1) 提出的堆叠双向循环自编码器能够实现运动数据到隐变量的重复映射与逆映射,提升了网络输出运动数据的平滑自然性。实验数据表明随着自编码器堆叠个数的增加,优化后运动数据平滑性逐渐提升,网络生成的运动数据平滑自然。

(2) 采用隐变量约束提高网络输出运动数据与动捕数据的感知真实性。实验结果表明,在网络训练过程中施加隐变量约束,本文方法生成的运动自然协调,具有较强的感知真实性。

(3) 采用滑窗方式对长运动序列进行处理,使得本文算法可以将Kinect数据转化为高精度动捕数据,实现低精度设备的采集数据高精度化。

1 相关工作

为优化Kinect捕获的不完整的运动数据,文献[10]提出了一种基于高斯过程模型的实时概率框架来提高Kinect捕获运动数据的准确性,其方法在自遮挡情况下,也能产生高质量的运动数据,然而由于高斯过程的计算复杂度高,该方法只适用于小型数据集;文献[11]使用基于高斯过程的局部混合方法提高求解速度,其方法允许局部模型实时增量更新,相比文献[10]能够处理更多数据样本。这2种方法都通过约束连续帧的速度变化来保证生成运动平滑,然而很难恢复转身的运动。文献[12]利用基于主成分分析的降维方法从运动数据库中搜索合适的运动数据来补全缺失值,并使用比例-微分(proportional-derivative,PD)控制器生成物理上可信的运动,这种运动恢复方法的准确性严重依赖数据库的内容和大小;文献[13]提出一种将局部姿态估计与全局检索技术相结合的方法,使用基于霍斯多夫距离的投票方法将2种假设结合起来,得到最终的运动姿态,其方法考虑了运动的连续性,能够有效解决因遮挡和噪声导致的数据缺失问题,然而对快速或绕垂直轴旋转超过45°的运动恢复效果较差。上述非深度学习类的Kinect数据去噪方法可以实现一些运动片段的处理,但对于可能包含任意运动的连续长序列运动处理效果不明显。

基于深度学习的运动数据优化方法近年来也逐渐发展起来。文献[6]使用EBD(Encoder-Bidirectional-Decoder)、EBF(Encoder-Bidirectional-Filter)2个神经网络来优化运动数据,其中神经网络EBD利用关节信息和时域相关性填补缺失数据,经由EBD降噪后的运动数据存在抖动以及噪声未完全清除的缺点,因此还需使用神经网络EBF做后续的平滑处理,但是该方法不能够用于提升运动数据的细节层次;文献[14]通过基于卷积神经网络的自编码器将Kinect运动数据进行映射和逆映射,但是生成的运动数据还存在一定的抖动;文献[15]使用深度循环神经网络(deep recurrent neural network,DRNN)分别处理Kinect数据的关节点三维坐标和速度,其结果分别记为pDRNN和vDRNN,使用卡尔曼滤波和k近邻算法整合增强pDRNN和vDRNN的结果来保证运动的自然性,也就意味着该方法还需要后处理步骤才可以生成平滑自然的运动;文献[7]提出的BRA网络能够实现对Kinect骨骼运动数据片段的优化,但是当数据的细节层次需要提高时,BRA难以保证优化后数据的感知真实性。

本文提出的算法目标是能够将Kinect骨骼运动数据序列自动转化为动捕数据,动捕数据的数据精度和细节层次都高于Kinect数据,因此算法需要能够去除噪声、能够确保细节层次提高后的数据具有感知真实性,使得输出的运动平滑自然,而且要能够对长运动序列作处理。

2 运动数据优化方法

2.1 运动数据集

为实现本文目标,首先需要构建Kinect和动捕设备2种运动数据采集设备同步采集的运动数据集。本文采用Kinect和诺亦腾Perception Neuron动作捕捉仪采集同步数据库,让表演者在采集环境中连续做常见运动,如打篮球、舞蹈、跳跃、步行等,获得一系列长运动序列。Kinect采集到的数据以关节点坐标格式保存,每帧数据包含25个关节点的三维坐标,因此每一帧运动数据的维度为75(25×3=75)。诺亦腾采集到的运动数据被转换为关节坐标格式,每帧数据包含59个关节点的三维坐标,因此每一帧运动数据的维度为177(59×3=177)。2种运动采集设备获取运动数据骨骼架构如图1所示。

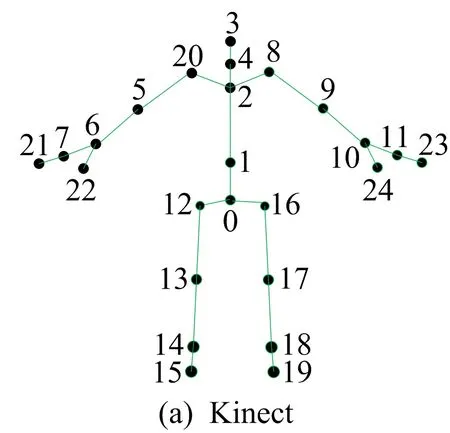
图1 运动数据骨骼架构

用2种设备获得运动序列后,需要对数据进行同步预处理:首先做空间上的处理,将2种数据都变换为以0号节点即根节点为基准的相对坐标数据;然后将2种运动数据做时间同步处理,因为诺亦腾动捕的采样频率为60帧/s,而Kinect的采样频率不稳定,约为30帧/s,所以以诺亦腾的采样率和时间域为基准,使用自然样条插值将Kinect数据上采样为60帧/s。预处理之后得到同步的“Kinect-动捕”长序列运动数据集,其中70%的数据作为训练集,30%的数据作为测试集。

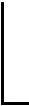
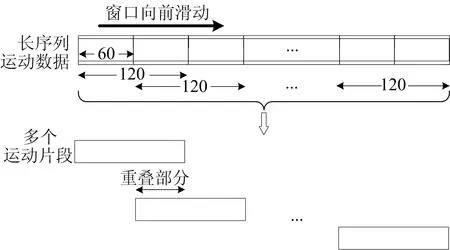
图2 滑动切片示意图

2.2 网络结构

本文提出的网络架构由堆叠双向循环自编码器与感知自编码器组成,如图3所示。

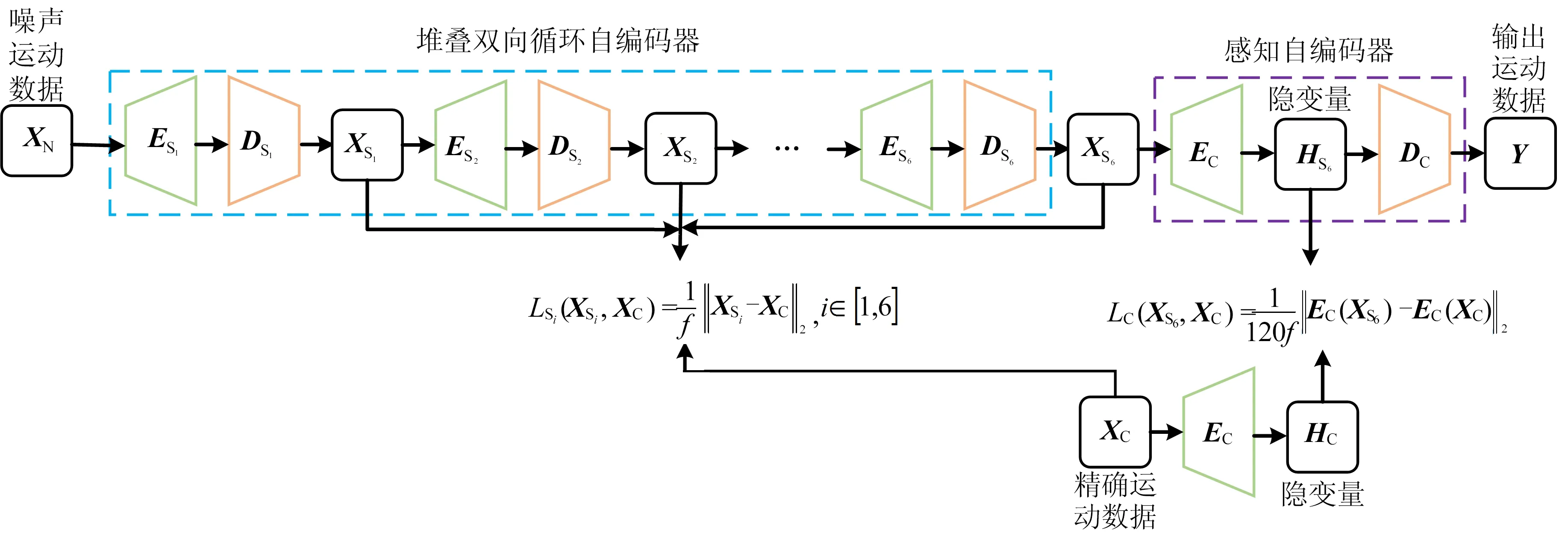
图3 堆叠自编码器网络结构

堆叠双向循环自编码器由6个双向循环自编码器(S1～S6)堆叠而成。在堆叠双向循环自编码器中,XSi=DSi(ESi(XSi-1)),其中:i为双向循环自编码器的序号,i=1,2,…,6;XS0=XN为首个双向循环自编码器的输入,即为噪声运动数据。最后一个双向循环自编码器的输出XS6作为感知自编码器的输入,感知自编码器的输出Y作为优化后运动数据。

本文网络结构中堆叠的6个双向循环自编码器结构与感知自编码器结构一致,如图4所示,其中双向循环自编码器由结构对称的编码器(encoder)和解码器(decoder)构成,均由3个全连接(fully connected,FC)层和1个Bi-LSTM单元组成,其中全连接网络有利于运动数据预测及缺损修复[16],Bi-LSTM单元更适用于处理具有时间序列特征的数据[7]。

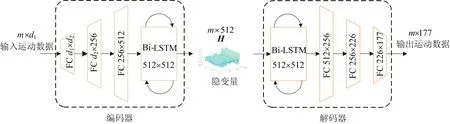
图4 双向循环自编码器结构

在编码器中运动数据到隐变量的映射过程中数据维度变化过程为:

其中,m为运动片段的帧数,在本文中m=120。在双向循环自编码器S1中,d1=75,d2=128;在双向循环自编码器S2～S6与感知自编码器中,d1=177,d2=226。

解码器与编码器对称,隐变量到运动数据的维度变化过程为:

编码器将含有噪声的人体骨骼运动数据映射到隐变量空间,解码器将隐变量映射回运动数据空间得到优化后的运动,本文方法通过首尾连接6个双向循环自编码器与一个感知自编码器,将运动数据进行重复的映射与逆映射,有利于获得平滑度更高的运动。

2.3 损失函数

本文设置了2类约束损失函数,分别是均方误差约束和运动学约束。

均方误差约束记为网络输出和标签数据之间的均方误差,运动学约束用于提升网络输出数据的运动学合理性,包括骨骼长度约束Lb、平滑性约束Ls和隐变量约束Lc。

2.3.1 均方误差约束

网络的输入数据为Kinect运动数据片段,标签数据为动捕运动数据片段,为此本文定义均方误差Lp为:

(1)

其中,f=120为训练数据的总帧数。需要重点指出的是,类似于堆叠沙漏模型[8],在本文方法中堆叠自编码器中的每个子编码器的输出都会用于与标签数据求均方误差,即(1)式中Y可以指代每个子自编码器的输出。

2.3.2 骨骼长度约束

骨骼长度约束用于堆叠自编码器。设堆叠自编码器输出Y在第i帧骨骼t的骨骼长度为:

(2)

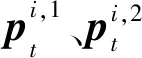
(3)

其中:lt为XC骨骼长度集合中的元素;J为关节点的个数。

2.3.3 平滑性约束

为确保优化后的运动序列在相邻帧间过渡平滑,本文对堆叠自编码器输出数据施加平滑性约束,首先重复自编码器的输出Y的边界元素得到Y′:Y(1,k)′=Y(2,k)′=Y(1,k),Y(f+1,k)′=Y(f+2,k)′=Y(f,k),Y(i,k)′=Y(i-1,k),1≤k≤177,2≤i≤f-1。其次,定义平滑矩阵O为:

(4)

平滑性损失函数为:

(5)

(5)式数值越小，证明运动越平滑。最小化‖OY′‖2相当于使自编码器输出的运动序列在前后两帧连续[4,17]。

2.3.4 隐变量约束

由于相似运动的隐变量相似,且可以在隐变量空间中对运动数据进行编辑,为提高优化后的数据与动捕数据的感知相似性,本文基于预训练的感知自编码器,记感知自编码器的编码器为EC,感知损失函数的定义为:

(6)

其中,EC(XS6)、EC(XC)分别为堆叠自编码器的输出XS6与动捕数据XC经由感知自编码器编码后的隐变量,将两者作比较得出XS6与XC的感知相似性。

2.4 训练方式

(1) 第1阶段仅使用训练数据集中所有的XC训练感知自编码器,对感知自编码器的输出YC施加均方误差约束、骨骼长度约束和平滑性约束,损失函数为:

L1=λc1Lp(YC)+

λc2Lb(YC)+λc3Ls(YC)

(7)

其中,λc1、λc2、λc3分别为3种约束的权重系数,本文设置λc1=1,λc2=λc3=0.000 2,训练迭代200次。训练完成后的感知自编码器的编码器和解码器部分分别记为EC和DC。

(2) 第2阶段训练基于隐变量约束的堆叠自编码器,对堆叠双向循环自编码器中每个自编码器的输出施加均方误差约束、骨骼长度约束和平滑性约束,并施加隐变量约束,损失函数为:

λsLs(XSi))+λcLc(XS6)

(8)

此阶段使用XN与XC进行网络训练,由于2种数据骨骼架构不一致,需加强骨骼长度约束和平滑性约束,设置权重系数λp=1,λb=λs=0.000 5,λc=1,训练迭代200次。

实验硬件处理器为Intel(R) Core(TM) i9-9900K,内存32 GiB,显卡为NVIDIA GeForce RTX 2080 Ti。实验基于TensorFlow框架,网络的学习率初始化为0.000 01,并使用Adam优化器动态调整各参数的学习速率。为避免过拟合,Bi-LSTM单元的dropout=0.2, batchsize设置为16。

2.5 长运动序列处理

长运动序列的滑窗处理示意图如图5所示。

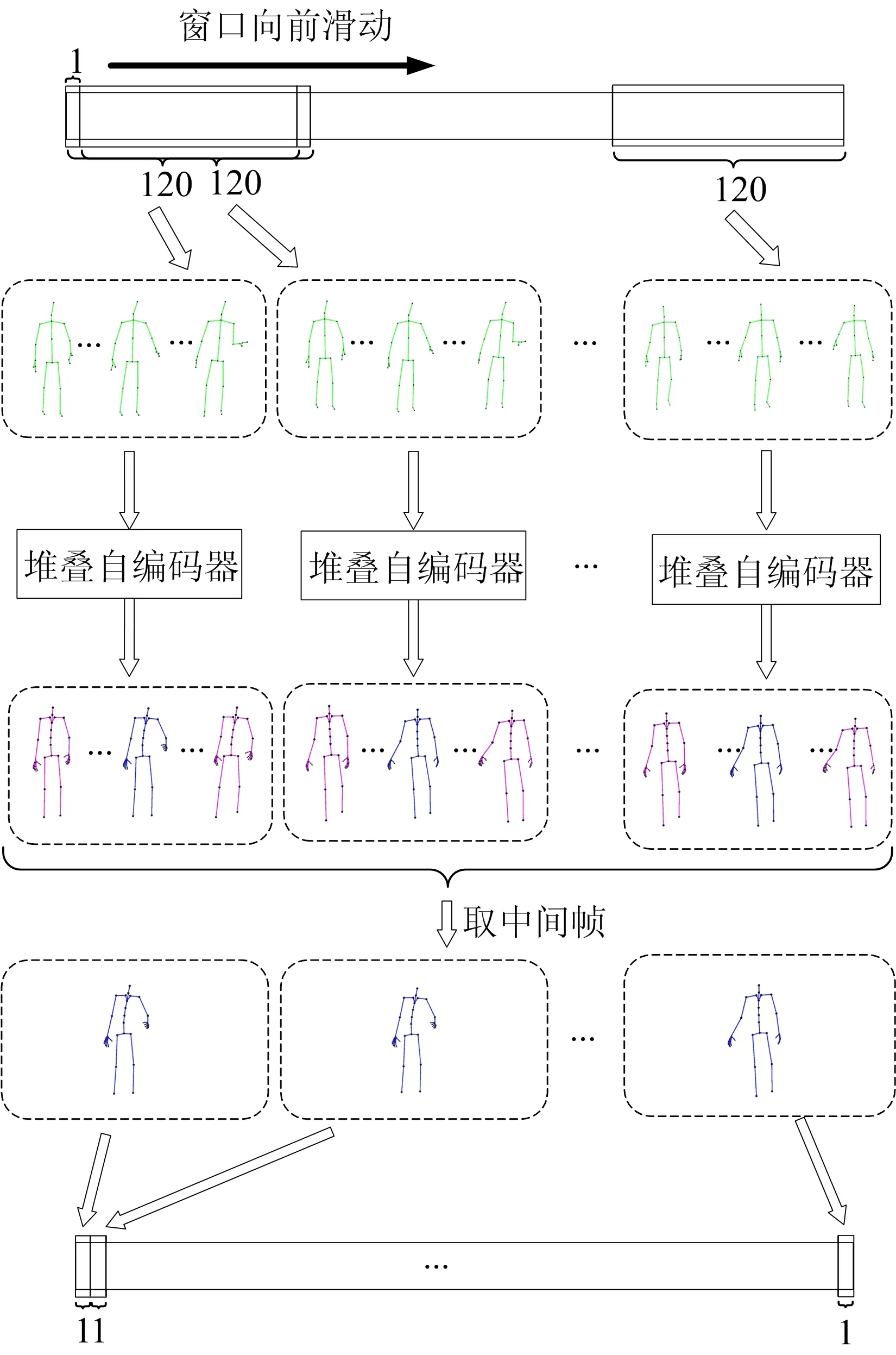
图5 长运动序列的滑窗处理示意图

实现Kinect采集数据的动捕化,即将Kinect获取的运动数据序列自动转化为具有动捕级精度的数据,因此需要算法能够处理Kinect获取的整个长运动数据序列。在训练阶段网络的输入和输出都是120帧的运动片段,因此在运行阶段需要对长序列作滑窗处理。本文采用宽度为120帧、步长为1的滑窗对整个长运动序列进行逐帧处理。设Xw,i为长序列在第i次滑窗操作中得到的运动片段,Yw,i为相应网络输出,Xw,i、Yw,i的长度均为120帧,但仅取Yw,i的中间帧放入最终优化序列中。

3 实验结果与分析

3.1 堆叠层数分析

本部分实验的目的是验证双向循环自编码器堆叠层数与网络输出数据平滑性的关系,为此,分别比较了堆叠层数为1、2、3、4、5、6的网络结构,分别记为BRA-S-1、BRA-S-2、BRA-S-3、BRA-S-4、BRA-S-5、BRA-S-6，见表1所列。

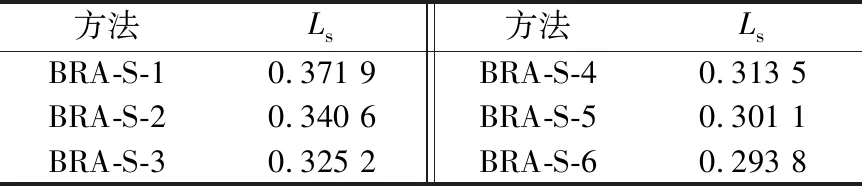
表1 堆叠次数与平滑性关系

由表1可知,堆叠模式可以提升运动数据的平滑性,但随着堆叠层数的增加,网络参数急剧增长,考虑到算法的计算效率和计算资源损耗,本文设置网络中双向循环自编码器的堆叠层数为6层。

3.2 隐变量约束分析及对比实验

本部分将证明隐变量约束可以提升优化后数据的感知真实性。

3种方法网络结构特征见表2所列,将不使用隐变量约束的方法记为BRA-S,而本文采用的添加感知约束的方法记为BRA-S-C。另外,由于本文方法是在文献[7]的BRA方法基础上提出的,为此在本部分将对比本文提出的BRA-S-C和BRA方法的效果。测试数据是同步后的“Kinect-动捕”长序列运动数据集。

表2 3种方法的网络结构特征

不同方法对一段对打篮球的长运动序列处理效果如图6所示,测试结果的某一帧中右手手腕的运动轨迹如图7所示。

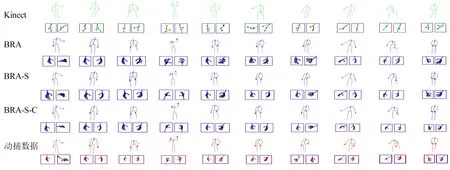
图6 运动序列处理效果对比

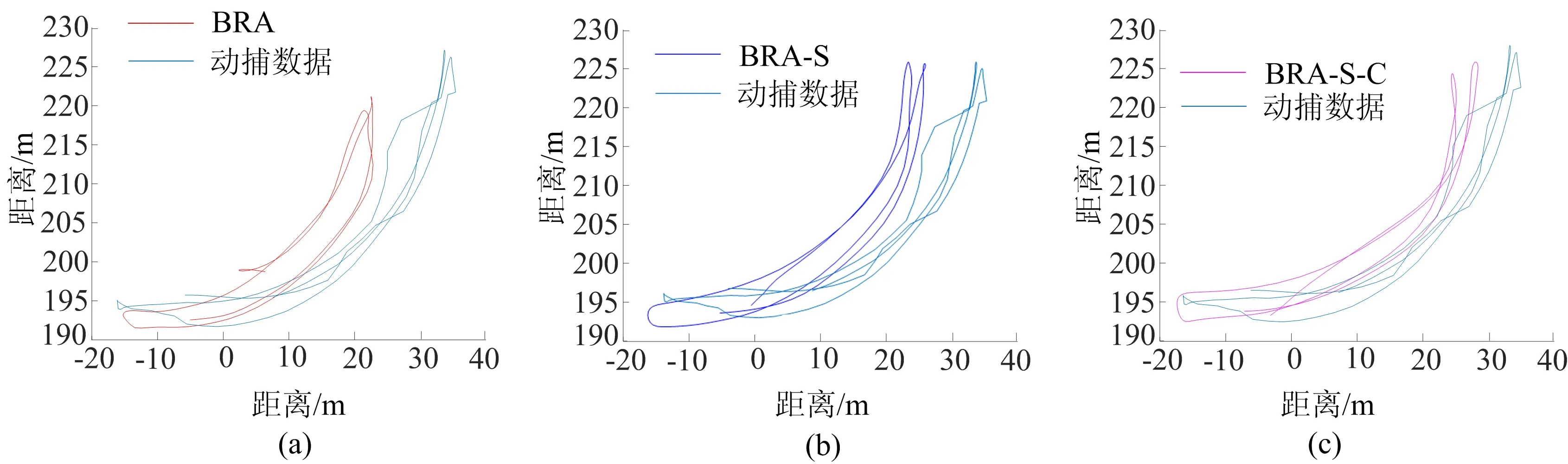
图7 运动轨迹对比

类似于文献[7],本文也采用均方误差、骨骼长度误差和平滑性误差来对比不同的方法,视觉效果已制作为视频,BRA、BRA-S、BRA-S-C 3种方法在测试长序列上的均方误差(Lp)、骨骼长度误差(Lb)、帧间平滑性误差(Ls)的均值见表3所列。

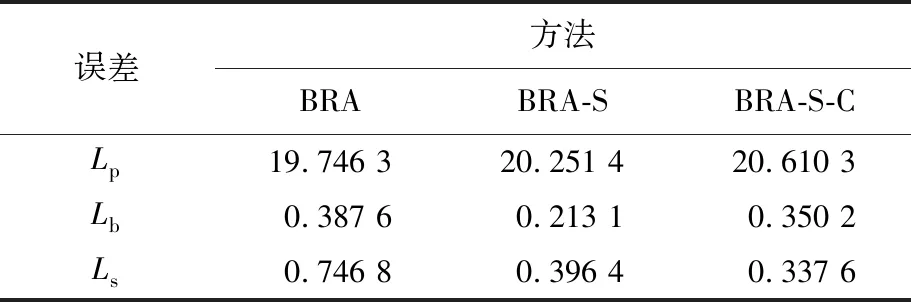
表3 3种方法整个测试数据集上的3种误差均值

表3中,BRA-S-C的Ls低于BRA-S,这从数值角度说明在网络中施加隐变量约束有利于提升运动数据的帧间平滑性。另外,BRA-S-C的Ls约为BRA的1/2,而且Lb也低于BRA,这说明BRA-S-C优化后的运动具有更好的平滑连贯性,骨骼长度更加稳定、不易跳变。

由图6可知,虽然BRA可以恢复出完整骨架,但出现手部骨骼扭曲的畸形现象,而BRA-S-C处理后的运动数据则不出现这种运动失真现象。虽然表3中BRA-S-C的Lp高于BRA,但图7中BRA-S-C得到的运动轨迹最能拟合动捕数据的运动轨迹,因此BRA-S-C的优化效果优于BRA,这得益于BRA-S-C的堆叠模式和隐变量约束:一方面堆叠模式提升运动数据的平滑性;另一方面隐变量约束在提升优化后数据与动捕数据的感知相似性的同时,能进一步提升帧间平滑性和运动自然性。

由于Kinect数据的单只手仅有4个关节点,而动捕数据的手部具有20个关节点,手部结构的稳定真实是评价算法输出是否具有感知真实性的重要标志。虽然表3中BRA-S-C的Lb略高于BRA-S,但在图6中,经BRA-S优化后的运动数据易在手部出现骨骼扭曲的运动不自然现象,而经BRA-S-C优化后的运动数据则不出现这种现象,从而说明隐变量约束有利于提升运动的自然性。隐变量约束通过提升网络生成数据与动捕数据的感知相似度,使得两者具有更强的一致性,网络生成的运动数据真实自然。

4 结 论

本文针对Kinect运动数据的动捕化问题,提出一种可对长序列进行处理的堆叠自编码器及其训练方法。网络由堆叠双向循环自编码器与感知自编码器组成,网络训练时用Kinect和动捕数据片段进行训练,在训练过程中对堆叠双向循环自编码器中每个双向循环自编码器的输出施加均方误差约束、骨骼长度约束以及平滑性约束,并对感知自编码器的隐藏单元施加隐变量约束。堆叠自编码器训练完成后,用滑窗的方式对长运动序列进行处理。实验结果表明,优化后的运动数据具有更好的感知真实性,运动序列平滑、自然,实现了基于低精度便捷设备获取高精度运动数据的目的。该项工作目前也存在一些不足,因为本文方法旨在获取平滑自然的运动,位置精度没有得到提高,所以在后期的研究工作中将设计加入残差网络,通过调整网络结构进一步提高运动数据的优化质量。