面向初始大曲率路径的驾驶员模型的构建研究

张 良,饶泉泉,续秋锦,祁永芳,李 鑫

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

0 引 言

在人-车-路构成的闭环系统研究中,人一直是汽车行驶稳定性和安全性的最大影响因素。因此,如何建立一个工作良好的驾驶员模型,使其控制性能与熟练并且具有高超驾驶技术的驾驶员操作行为基本一致,成为当前研究的热点和焦点。文献[1]研究了基于单点预瞄最优曲率模型建立的单轨车辆转向时的驾驶员模型，但未对其神经网络进行研究;文献[2]研究了基于二自由度车辆模型的三点预瞄驾驶员模型,并用智能控制补偿对方向盘转角进行补偿校正,但未结合先进的神经网络进行分析;文献[3]研究了基于模糊控制的驾驶员模型,并将其与真实驾驶员进行了对比验证,但未结合预瞄驾驶员模型进行研究;文献[4]研究了基于模型预测控制(model predictive control,MPC)的自动驾驶车辆横向路径跟踪控制模型,分析了预瞄时间和车速对车辆跟踪参考路径的影响,但未对特定工况的路径进行分析;文献[5]研究了基于三维批量归一化视觉几何组融合的行为识别,并设计长短期记忆(long short-term memory,LSTM)神经网络解决深度学习算法准确性低、计算量大的问题,但未应用于驾驶员模型领域。综合上述研究可知,目前结合驾驶模拟器对初始大曲率路径下各种驾驶员模型鲁棒性的比较研究很少。

本文在驾驶模拟器获得驾驶员真实数据后,对比基于单点预瞄的驾驶员模型与基于LSTM的驾驶员模型的路径跟随能力,利用Matlab/Simulink以及python进行仿真分析,验证了基于LSTM的驾驶员模型比基于单点预瞄的驾驶员模型具有更强的鲁棒性和更好的行驶安全性。

1 单点预瞄的驾驶员模型搭建

1.1 单点预瞄驾驶员模型原理

单点预瞄驾驶员模型是在已知车速、给定预期路径下建立的。它可以根据预期车速和预期路径信息,通过设定的预瞄时间,控制汽车的方向盘转角,从而达到路径跟随的效果。

为使问题简化,假设一个小曲率的路径，以分析单点预瞄的实现过程。假定汽车以恒定车速行驶,且横向位移相较于纵向位移来说很小。基于此假设可以认为单点预瞄的驾驶员模型是为了实现横向路径的跟随。设汽车预期的横向位移为f(t),汽车当前实际的横向位移为y(t),预瞄时间为T,驾驶员对当前方向盘的操作是希望在经历预瞄时间T后,使汽车实际的横向位移y(t+T)近可能逼近汽车预期的横向位移f(t+T),记为fe[6]。

恒速状态下预瞄跟随模型原理如图1所示。

图1 恒速状态下预瞄跟随模型原理

(1)

(2)

(3)

驾驶员由于其生理限制,仅依靠(3)式决策出的方向盘转角难以对汽车实现可靠控制。因此,综合各种复杂情况后提出了考虑驾驶员生理因素的单点预瞄驾驶员模型流程,如图2所示。

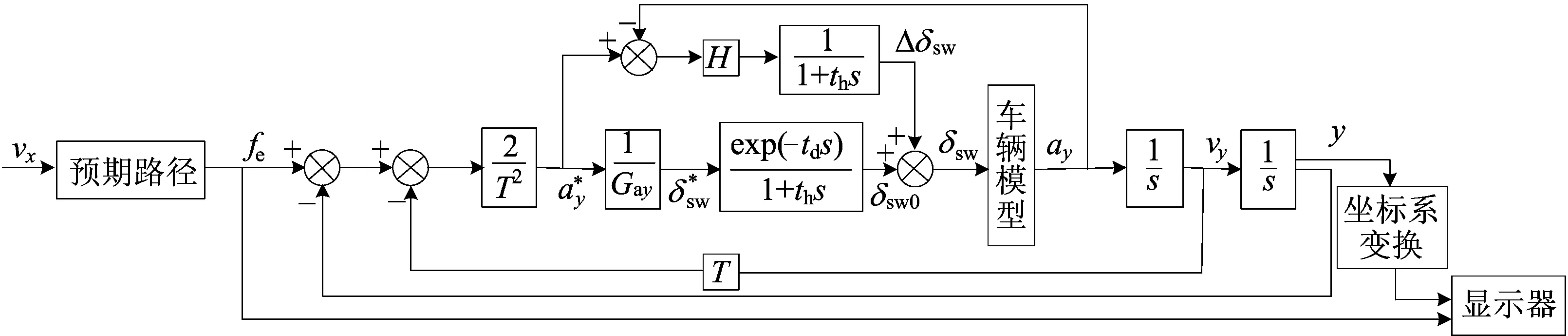
图2 考虑驾驶员生理因素的单点预瞄驾驶员模型流程

(4)

其中,H为加速度反馈系数。采用这种修正可以弥补由于驾驶员反应滞后以及各种原因引起的Gay与实际车辆横向加速度增益不符造成的误差,使驾驶员模型具有很强的鲁棒性。例如,汽车在低附着路面上行驶,由于路面摩擦因数的限制使得侧向加速度增益降低,这时使用高附着路面上得到的Gay决策出的方向盘转角偏小,汽车的实际横向加速度偏小,采用横向加速度反馈后就会增加一个附加的方向盘转角,以补偿Gay失配造成的误差。驾驶员模型最后决策出的方向盘转角δsw为δsw0与修正量Δδsw之和。最后，将经过坐标变换后的实际横向位移和预期横向位移输入到显示器进行观察比较。

1.2 二自由度车辆模型

二自由度车辆模型在获取车辆位置信息、转向盘转角结果时，相较于四自由度或七自由度车辆模型具有控制参数少、控制性能好的优点。因此，本文采用二自由度汽车模型,如图3所示。

图3 二自由度汽车模型

车辆坐标系原点与汽车质心重合[8]。各参数的物理意义如下:δ为前轮转角;β为质心侧偏角;ξ为航向角;u1、u2分别为前、后轴中点的速度;α1、α2分别为前、后轴侧偏角;FY1、FY2分别为地面对前、后轮的侧向反作用力,即侧偏力;v1为汽车的绝对速度;u为汽车绝对速度在车辆坐标系x轴方向的分量;v为汽车绝对速度在车辆坐标系y方向的分量;wr为汽车横摆角速度;a为质心至前轴的距离;b为质心至后轴的距离;L为轴距。

先对二自由度汽车模型进行汽车动力学分析,得到汽车质心绝对加速度在车辆坐标系x轴和y轴方向的分量,即

(5)

再对车辆运动模型进行动力学分析,可知外力、外力矩与汽车参数之间的关系式为:

(6)

其中,k1、k2分别为前、后轮的侧偏刚度。

由(4)式和(5)式可以得出二自由度汽车的运动微分方程为:

(7)

选取质心侧偏角β和横摆角速度wr为状态变量,即x=[βwr]T;方向盘转角δ作为输入量,即u=δ。

(8)

对应的矩阵形式为:

(9)

其中

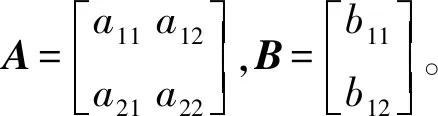
将质心侧偏角β、横摆角速度wr及侧向加速度ay作为状态空间的输出,便于后续对驾驶员模型的操纵稳定性进行分析[9],即y=[βwray]T,得到输出方程y=Cx+Du为:

(10)

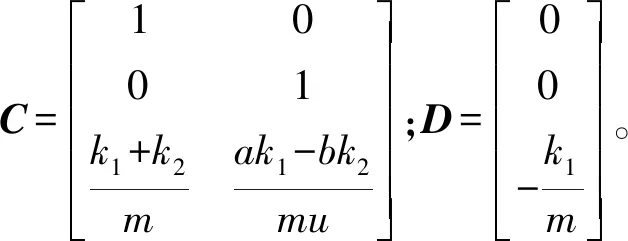
1.3 坐标系变换

由于驾驶员-汽车闭环系统采用二自由度汽车模型,该模型所输出的横向加速度是基于车辆坐标系的[10]。这也符合驾驶员模型对于驾驶员开车行为的模仿，因为驾驶员在操纵汽车行驶时,驾驶员预瞄前方道路信息所参考的方向与汽车行驶的方向一致。

为了将实验及仿真获得的结果做对应分析,有必要对车辆坐标系进行坐标变换[11]。车辆坐标系变换到大地坐标采用的转换方程为：

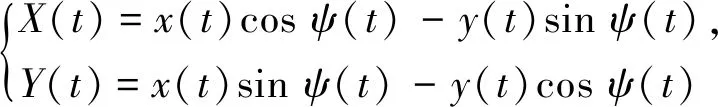
(11)

其中:(X(t),Y(t))为汽车在某一时刻大地坐标系下的坐标;(x(t),y(t))为车辆坐标系下的坐标;ψ(t)为该时刻汽车的航向角。

2 基于LSTM的驾驶员模型搭建

2.1 LSTM原理

LSTM的结构如图4所示。LSTM减少了递归神经网络中消失和爆炸梯度,并可以很好地解决长时依赖的问题,因此得到了广泛的应用。

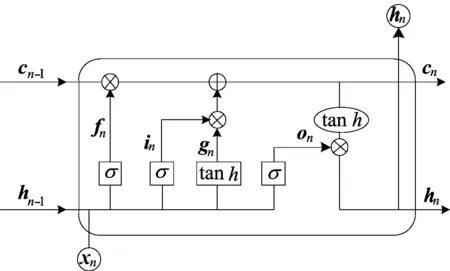
图4 LSTM神经网络

从LSTM的结构可以看出,获取前一时刻输入信息cn-1和hn-1后,由输入信号与输入门in、遗忘门fn、输出门on之间的关系式可以得到下一时刻的输出信息。

关系式如下：

in=σ(Wixxn+Wihhn-1+Wiccn-1+bi)

(12)

fn=σ(Wfxxn+Wfhhn-1+Wfccn-1+bf)

(13)

on=σ(Woxxn+Wohhn-1+Woccn-1+bo)

(14)

gn=tanh(Wcxxn+Wchhn-1+bc)

(15)

cn=in×gn+fn×cn-1

(16)

hn=on×tanh(cn)

(17)

其中：W*(*=ix,ih,ic,fx,fh,fc,ox,oh,oc,cx,ch)表示权重矩阵;b*(*=i,f,o,c)表示偏置向量;tanh(·)表示双曲正切函数,即

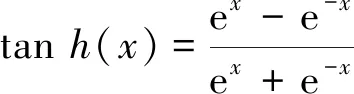
(18)

这些门的使用允许LSTM决定是否保留现有记忆或在现有记忆上权衡新信息,使得LSTM可有效作用于驾驶员模型的决策初始大曲率路径优化中。

2.2 LSTM应用

汽车在道路上行驶时不会突然停止,也不会瞬间移动,这意味着汽车的行驶轨迹是连续的,驾驶员的方向盘转角也是连续的。因此,可以通过顺序建模方法来构建驾驶员模型,即将汽车在道路上的行驶按时间顺序采集到的数据加载到LSTM神经网络中进行路径跟随。在道路上行驶时,影响驾驶员转向操纵的2个主要因素是车速和道路曲率[12]。基于LSTM的驾驶员模型如图5所示。

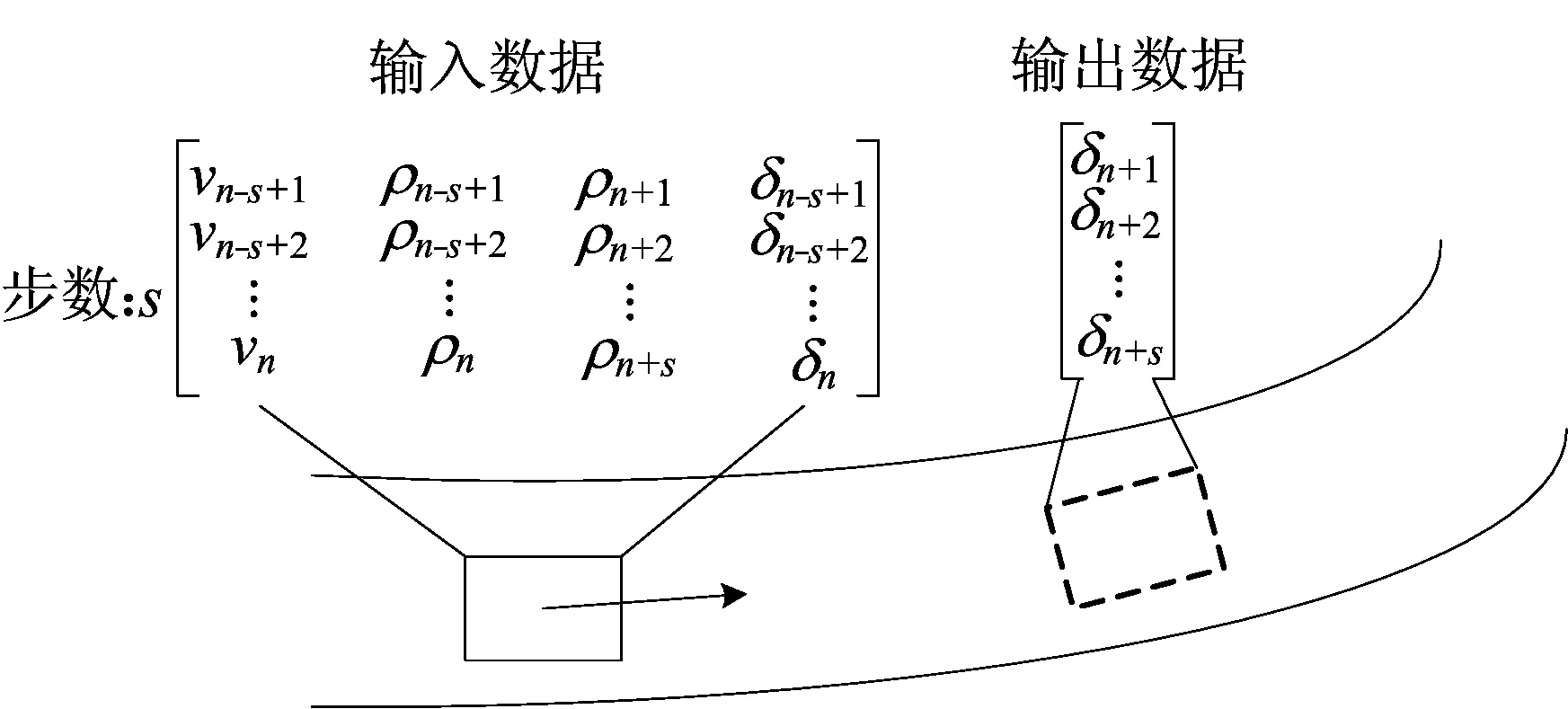
图5 基于LSTM的驾驶员模型

LSTM的输入层为历史速度[vn-s+1vn-s+2…vn]、历史道路曲率[ρn-s+1ρn-s+2…ρn]、未来道路曲率[ρn+1ρn+2…ρn+s]、历史方向盘转角[δn-s+1δn-s+2…δn],输出层是未来方向盘转角[δn+1δn+2…δn+s]。本文考虑的是恒定速度下初始大曲率路径的驾驶员模型路径跟随问题,因此速度项均为定值。

基于LSTM的驾驶员模型由1个输入层、2个隐藏层和1个输出层组成。其中隐藏层含有的节点为100个。在训练之前,应用归一化原理将特征数据进行线性缩放。LSTM的学习率为0.001,学习纪元数为100；设置步长s为5,表示利用前0.05 s的输入数据来预测之后0.05 s的输出数据。这些均在编程语言python中实现,并且使用jupyter notebook的IDE进行代码编写及运行。

3 实验结果

3.1 实验装置

实验使用合肥工业大学现有的驾驶模拟器,它由仿真硬件平台、已校准的车辆模型和试验管理软件共同组成,并将其整体称为硬件在环(hardware-in-the-loop,HIL)系统,如图6所示。

图6 HIL系统基本组成

选定车辆模型,设置预期路径,搭建控制模型,利用驾驶模拟器进行相关的实验操作,如图7所示。

图7 驾驶模拟器实验过程

仿真硬件平台提供满足车辆模型实时运行的仿真环境,模拟待测控制器正常运行所需的所有输入信号,并采集控制器发出的控制命令;车辆模型为Carmaker车辆动力学模型;软件平台用于搭建和配置HIL测试软件工程,对待测试过程进行实时监测和在线调参。

3.2 实验分析

因为本文探讨的是初始大曲率的特殊工况,所以在建立预期路径时设置初始曲率K=3.36的大曲率路径,其中K为初始位置的曲率。实验结果主要分为2类:一类由设置的预期路径、驾驶模拟器仿真的真实路径、基于单点预瞄仿真的路径以及基于LSTM仿真的路径组成;另一类由驾驶模拟器仿真的方向盘转角、基于单点预瞄仿真的方向盘转角以及基于LSTM仿真的方向盘转角组成。

4条路径随时间变化的曲线如图8所示。

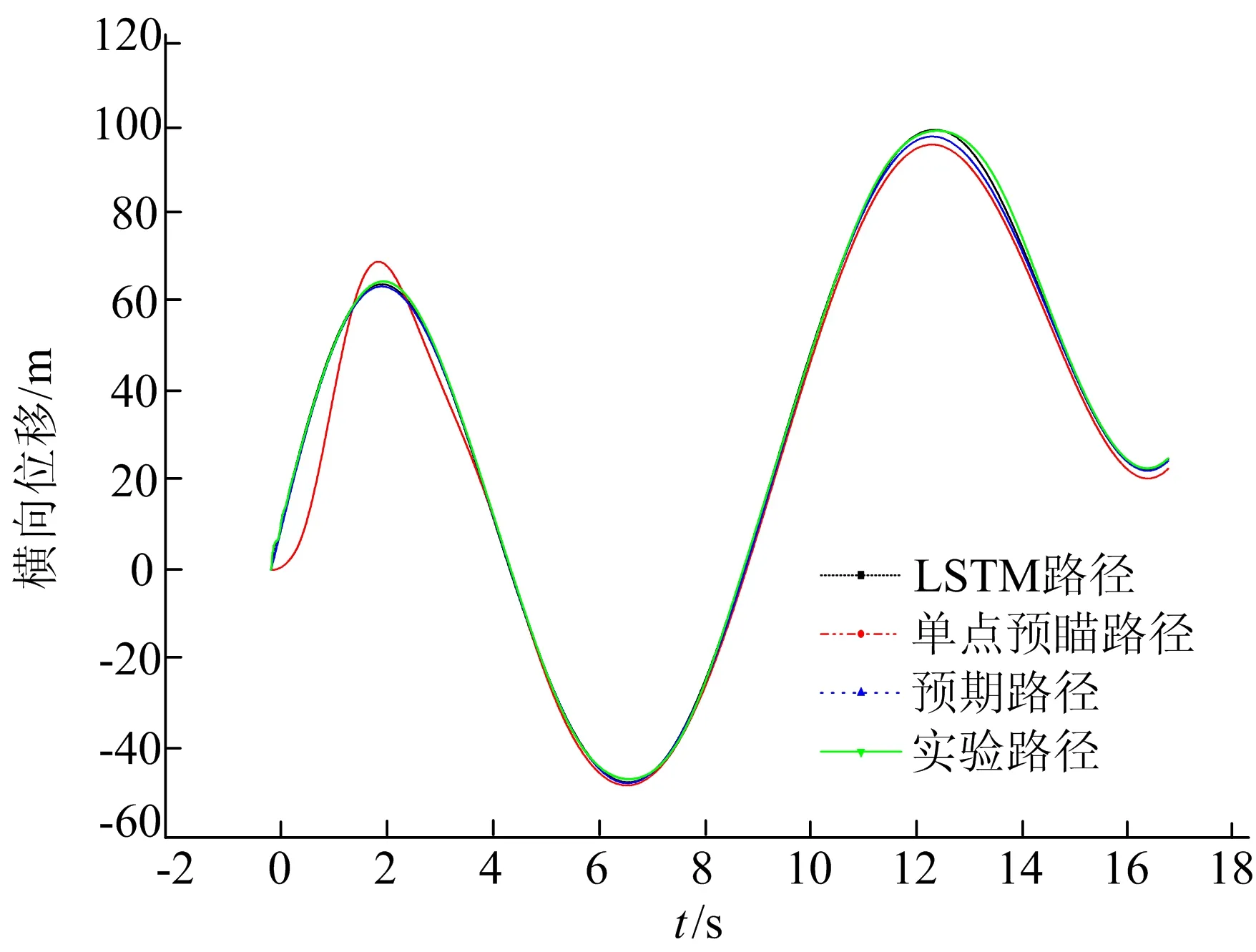
图8 横向位移随时间变化的曲线

3个方向盘转角随时间变化的曲线如图9所示。

图9 方向盘转角随时间变化曲线

实验结果设定的路径为初始大曲率路径,并且由驾驶模拟器获得当驾驶员控制车辆时获得的真实路径。对比分析实验结果可知，基于LSTM的驾驶员模型比基于单点预瞄的驾驶员模型在初始大曲率路径的横向控制和方向盘转角控制上有更好的结果。

4 结 论

本文通过设置初始大曲率路径,在驾驶模拟器仿真的真实驾驶员数据上,比较基于单点预瞄的驾驶员模型与基于LSTM的驾驶员模型对于路径跟随的能力。实验及仿真结果表明,在初始大曲率路径的跟随性能上,基于LSTM的驾驶员模型明显优于基于单点预瞄的驾驶员模型,因此可以认为基于LSTM的驾驶员模型具有较强的鲁棒性和行驶的稳定性。本研究后期会将LSTM应用于实车试验,为智能汽车的安全行驶提供有效的参考。