基于VMD和SVM的煤厚预测方法研究

曾爱平，张嘉玮，任恩明，刘 涛，姜 飞，刘兴金，苏怀瑞

基于VMD和SVM的煤厚预测方法研究

曾爱平1,2，张嘉玮3，任恩明1,2，刘 涛1,2，姜 飞1,2，刘兴金1,2，苏怀瑞1,4

(1. 山东省深部冲击地压灾害评估工程实验室，山东 济南 250104；2. 山东省煤田地质局物探测量队，山东 济南 250104；3. 中国矿业大学 资源学院，江苏 徐州 221116；4. 山东省煤田地质规划勘察研究院，山东 济南 250104)

煤厚变化对煤炭安全高效开采具有重要的影响。针对三维地震数据中含有噪声时，易导致煤厚预测结果具有较大误差的问题，提出一种利用变模态分解(VMD)和支持向量机(SVM)方法结合进行煤厚预测的方法。首先，构建煤厚楔形模型并对其进行地震正演模拟，当煤层厚度较薄时，振幅属性和频带宽度属性与煤厚之间具有较好的正相关性，而瞬时频率属性与煤厚具有较好的负相关性；对正演地震记录增加噪声，结果表明噪声对利用地震属性进行煤厚预测具有较大影响。利用VMD进行去噪之后，基于SVM进行煤厚预测，实际地震资料的煤厚预测结果与已有钻孔揭露的煤层信息较为吻合，预测煤厚最小绝对误差仅为0.02 m，最大绝对误差0.52 m，验证了方法的可行性和有效性。研究成果可为低信噪比区的煤厚反演提供参考。

变模态分解；支持向量机；煤厚；地震属性

在现代化大型矿井的建设和生产过程中，煤炭储量的计算、开采的合理布设都需要准确了解煤层厚度的变化[1]。据有关资料统计结果显示，如果实际煤层厚度比原定设计煤层厚度变薄10%～20%，那么煤炭的产量将会下降35%～40%[2]。因此，煤层厚度是煤矿设计与开采必不可少的数据，准确预测煤层厚度，不但能给煤矿提供有力的地质保障，还能带来巨大的经济效益[3]。对于深部开采的煤矿，冲击地压灾害的频度和强度与煤层厚度及其变化密切相关[4]。而煤层在地震勘探中属于薄层，但薄层厚度的定量预测一直是公认的难题之一。目前常用的钻孔内插法预测煤厚的方法并不能保证远离钻孔位置的煤厚精度；地震波振幅或频率域参数预测煤厚(如调谐法，谱矩法等)受地震数据的信噪比与保真度的影响大，多解性强，一般只能预测煤厚的横向变化趋势，而很难得到精确的结果。实际上，煤层厚度呈非线性空间变化，如何构建一种非线性的煤厚预测方法是亟待解决的问题，这对矿井高效开采和安全部署均有着重要的意义。

国内外学者在煤厚预测方面进行了大量研究，取得了较为显著的成果与进展。孙渊等[5]通过提取不同频段的小波域地震属性，利用人工神经网络技术实现了煤厚的定量预测；郭银景等[6]总结了槽波地震勘探技术在探测煤层和预测煤厚方面的工作和应用现状； Liu Zuiliang等[7]研究结果表明，槽波数据中折射P波的周期性与煤层厚度成正比，运用折射P波的周期可以预测煤厚；赵凯[8]通过实际资料验证了应用槽波勘探资料预测煤厚的方法具有较高的准确性；杨文强[9]根据地震相与沉积相的对应关系，应用煤层反射波形的变化预测煤层厚度；张宪旭[10]提出基于模型驱动的煤层强反射能量衰减方法预测煤层厚度，同时提升了煤层附近的弱反射层成像质量。为了提高煤厚预测的精度，学者们还通过对大量数据进行统计，研究煤厚变化的规律。杜文凤等[11]利用协克里金法预测煤层厚度，有效地降低了煤厚预测的误差；程彦[12]结合变异函数和克里格法对大量煤厚数据进行统计，归纳分析了煤层反射波的地震属性随煤层厚度变化的规律，进而预测煤厚。但以上煤厚预测方法较少讨论噪声对煤厚预测结果的影响，而通常情况下，地震资料均受到一定程度的噪声影响。同时，人工智能方法在地震勘探应用领域亦有了较为广泛的应用，并取得了较好的应用效果，但人工智能方法在煤厚预测中的应用还较少。

在地震信号去噪方面，变分模态分解(Variational Mode Decomposition，VMD)是一种自适应、高效的信号分解方法，该方法根据信号自身的特征将其分解为一组独立的本征模态函数。孙远[13]、张杏莉[14]等通过研究被广泛应用于矿业工程领域的微震监测技术，并提出了将VMD和小波能量熵(Wavelet Energy Entropy，WEE)结合的降噪算法，从而提高了微震信号的信噪比。李晋等[15]利用了VMD对时间域序列中的大尺度强干扰的去噪能力，并运用匹配追踪(MP)保留了重构信号中较多的低频缓变化信息，有效地压制了近源干扰。因此，基于VMD方法的优势，其可以很好地被应用在具有非线性和非平稳特性的地震信号去噪中。

在人工智能方面，支持向量机(Support Vector Machines，SVM)是20世纪90年代初由Corinna Cortes等根据统计学习理论提出的一种新的机器学习方法[16]。袁志明等[17]针对SVM模型基于单点数据建模的缺点，建立了粒子群优化算法(Particle Swarm Optimization, PSO) 和SVM模型顾及邻近点，并进行最优训练样本数量研究，得到了最优短期样本的预测效果。支持向量机以结构风险最小化为准则，通过对函数子集和子集中判别函数的适当选择，使实际风险达到最小，保证了在样本有限的情况下获得的最小误差预测模型在应用独立测试集进行测试时，误差仍然较小。

综上，为了解决地震信号中含有噪声时，易导致煤厚预测结果具有较大误差的问题，同时为了将人工智能方法引入煤厚预测中，笔者提出将VMD和SVM相结合进行煤厚预测的方法。该方法首先对地震信号进行变模态分解，有效去除随机噪声；然后提取对煤厚响应敏感的地震属性，并选取合适的地震属性，利用支持向量机进行学习和训练，最终实现煤厚的定量预测。

1 VMD和SVM预测煤厚的基本原理

1.1 VMD原理

VMD是一种自适应的、非递归的、可将信号分解成有限的分量信号(IMF)之和的分解方法[2]。基于 Wiener 滤波、Hilbert 变换与外差解调所形成的一种新型分解算法，采用 VMD 处理非平稳信号时可以有效避免经验模态分解( Empirical Mode Decomposition，EMD) 类算法导致的模态混叠效应和端点效应，将 IMF 重新定义为一个调幅–调频信号[4]。它有着牢靠的数学理论基础，而且能较好地解决模态混叠问题。VMD的分解步骤如下[3]：

①对于每一个模态，通过Hilbert变换计算与之相关的解析信号；

②对于每一个模态，通过加入指数项调整各自估计的中心频率，把模态的频谱变换到基带上；

③带宽可以通过对解调信号进行H高斯平滑进行估计。

这样就可以得到一个变分约束问题，然后采用二次罚函数项和拉格朗日乘子算子得到一个无约束问题，根据函数的迭代关系满足条件后输出IMF，并重构原信号从而求解问题。

()为观测的采样信号，u()为分解得到的基函数，为惩罚因子，为基函数对应的中心频率，则约束对象为[18]：

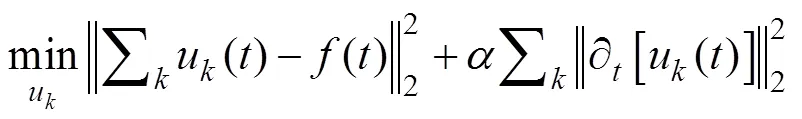
转化为频率域，再求极值：

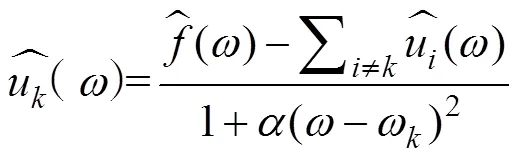
式中：为时间；为信号分解后基函数个数；为样本点。

每个基函数基于其他的基函数更新，相当于每个基函数是原信号剩余部分的低通滤波，每次迭代都是保留剩余信号的低频部分。

1.2 SVM回归

SVM是建立在统计学习理论基础上的一种数据挖掘方法。支持向量机是建立在统计学习理论基础上的一种小样本机器学习方法，它根据有限样本信息，在模型复杂性和学习能力之间寻找最佳折中，以期获得最好的泛化能力。支持向量机回归机基本原理如下[18]：

假设回归函数()为拟合数据时，需寻找一个尽可能小的。为此，采用最小化欧几里得空间的泛数。其中，和分别为回归函数的法向量和偏移量，并假设所有的训练数据在精度下无误差地拟合函数，可以得下面的优化问题[16,19]，即：

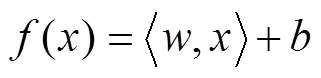
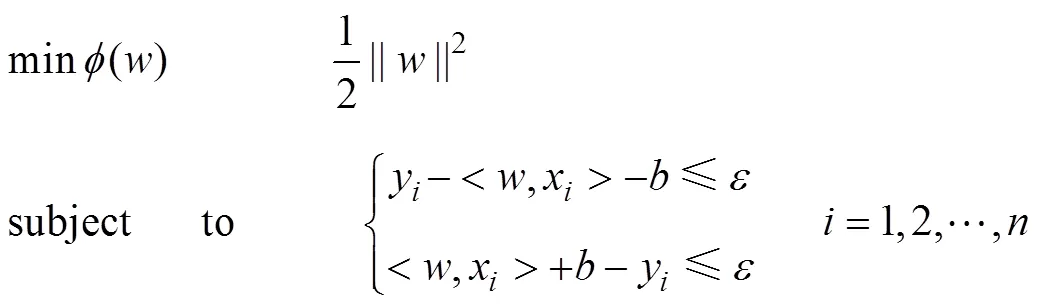
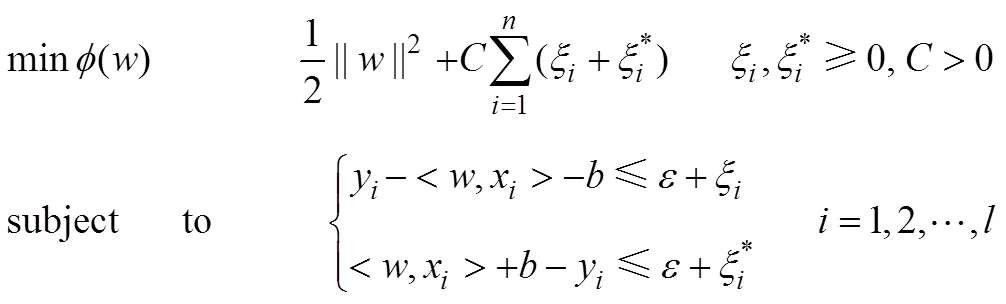
1.3 VMD-SVM的煤厚预测流程

首先，利用VMD对地震数据进行分解，选择IMF2分量提取瞬时振幅、瞬时频率等地震属性。选取一定数量的样本，对其进行SVM煤厚训练，然后利用训练模型，进行煤厚预测。具体流程如图1所示。

图1 VMD-SVM煤厚预测流程

2 楔形模型试算

2.1 煤层楔形模型及其地震属性分析

本文首先构建常用于储层厚度研究的楔形模型，如图2a所示。煤厚0～40 m，主要岩性砂岩、泥岩和煤层，各层的纵横波速度、密度及厚度，具体情况见表1。利用主频为50 Hz的雷克子波进行正演模拟，接收道距为10 m，共40道接收，正演剖面如图2b所示。

表1 煤层地质模型参数

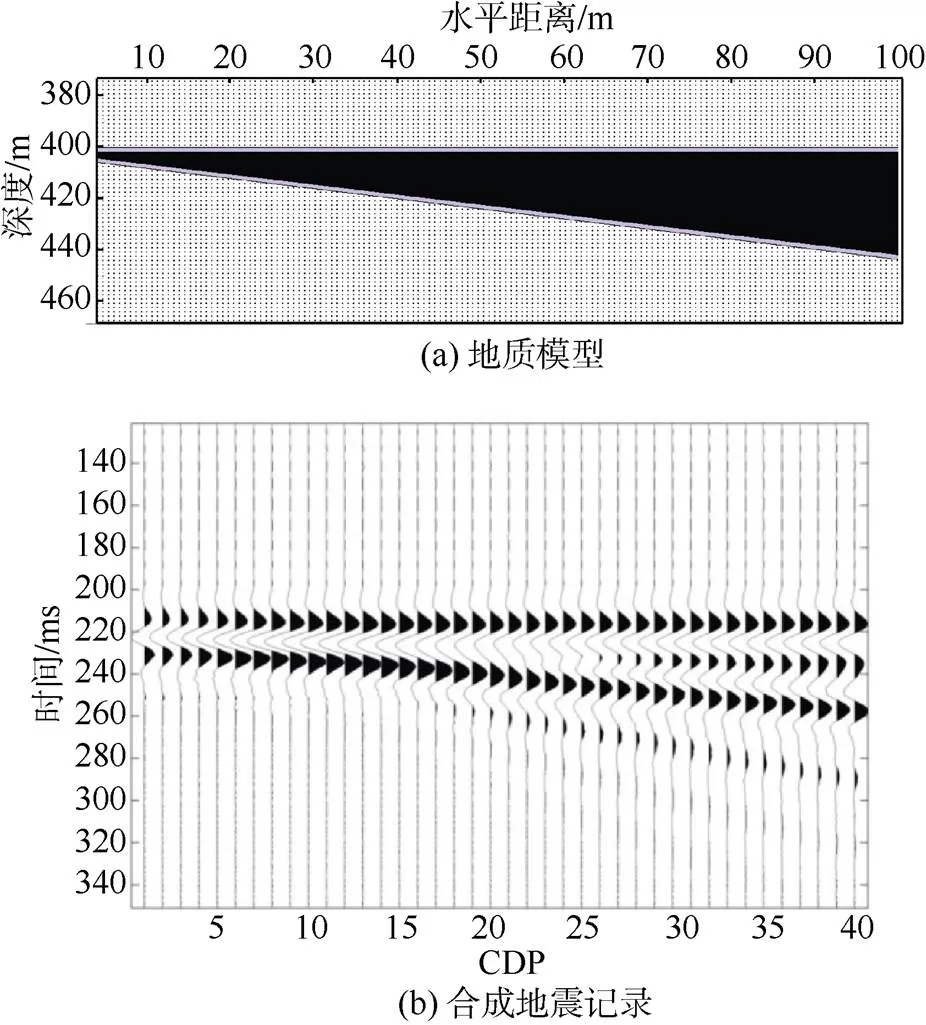
图2 楔形地质模型正演

提取楔形模型正演地震剖面中的振幅和频率属性，并对其响应特征进行分析。楔形模型的振幅属性如图3a所示，随着煤厚的增加，振幅属性增大，当煤厚达到12 m(约1/4个波长)时，振幅达到最大值。随着煤厚的继续增加，振幅属性逐渐降低并趋于平缓变化。当煤层厚度小于12 m时，振幅属性与煤厚具有较好的正相关性。楔形模型的瞬时频率属性如图3b所示，煤层厚度小于15 m时，瞬时频率属性随着煤厚的增加逐渐降低并趋于最小值，瞬时频率属性与煤厚具有较好的负相关性，然后随着煤层厚度的增加，逐渐平缓增大并趋于稳定。楔形模型的频带宽度属性如图3c所示，煤层厚度小于12 m时，频带宽度属性随着煤厚的增加逐渐增加，频带宽度属性与煤厚具有较好的正相关性；煤层厚度大于12 m，小于25 m时，随着煤层厚度的增加，逐渐降低并趋于最小值；煤层厚度大于25 m后，逐渐平缓增大并趋于稳定。

因此，当煤层厚度较薄时，振幅属性和频率属性与煤厚之间的关系相对简单，存在单调非线性关系，可以利用地震属性进行煤厚的预测。

2.2 添加噪声的楔形模型和VMD分解

对图2b所示的楔形模型地震剖面添加40 dB的随机噪声，所加的噪声为高斯噪声，且满足均值为0、方差为1的独立平均分布，结果如图4所示，增加噪声之后，煤层地震响应特征受到了一定程度的影响。提取振幅和频率属性，其结果如图5所示。因为噪声的影响，煤厚与各地震属性的对应关系变化较大，即使在煤层较薄时，煤厚与各地震属性之间的关系变得较为复杂，不存在明显的正或负相关性，不利于利用地震属性进行预测煤厚。

图3 楔形模型的地震属性

而VMD是一种完全非递归、自适应的信号分解方法，可有效地用于地震信号的去噪。图6是对含噪声的楔形模型合成地震记录进行VMD分解去噪之后的结果。利用VMD进行去噪之后，楔形煤厚模型的地震响应特征得到了较好的恢复，与无噪合成地震记录基本一致。

图7是对不含噪和含噪楔形模型VMD结果提取地震属性所得结果，各地震属性与煤厚之间的关系与不含噪声情况下的结果具有基本一致的趋势。所加的噪声为高斯噪声，且满足均值为0、方差为1的独立平均分布，在此条件下，瞬时振幅一致性最好，瞬时频带次之，瞬时带宽受噪声的影响较为明显，但其变化趋势基本吻合。当煤厚小于12 m时，瞬时振幅随煤厚增大，瞬时频率降低，而频带宽度则是先增加然后降低。因此，基于VMD去噪处理之后提取的地震属性，更有利于进行煤厚的预测。

基于支持向量机回归机算法开展楔形模型煤厚的预测。楔形模型总共有40道，为了保障样本的多样性，选取1、3、5、7、10、13、15、17、20、23、25、27、30、33、35、37、40道，共计17道地震记录的振幅、瞬时频率和频带宽度属性作为训练集输入样本，其对应的厚度为训练集输出样本。其他23道地震记录的属性作为测试集。分别利用支持向量机进行无噪声、含噪声和VMD去噪的地震属性煤厚预测，结果如图8a所示。无噪声情况下预测的煤层厚度结果与实际煤层厚度值变化趋势基本一致；含噪声时煤厚预测值与真实值存在明显的误差，尤其在煤厚较薄和较厚时误差结果较大。经过VMD去噪处理之后的数据，煤厚预测结果较含噪声时有了较大的改善。煤层厚度在30～40 m时，预测结果存在一定的误差，分析其原因可能为该厚度煤层的地震属性变化相对剧烈，导致预测结果的不稳定。楔形模型在3种情况下的煤厚预测绝对误差如图8b所示，由图8可知，含噪声情况下绝对误差值均较大，最大达到32 m；而VMD处理之后的预测结果，绝对误差值均较小，仅当煤厚较大时，绝对误差有所增加。

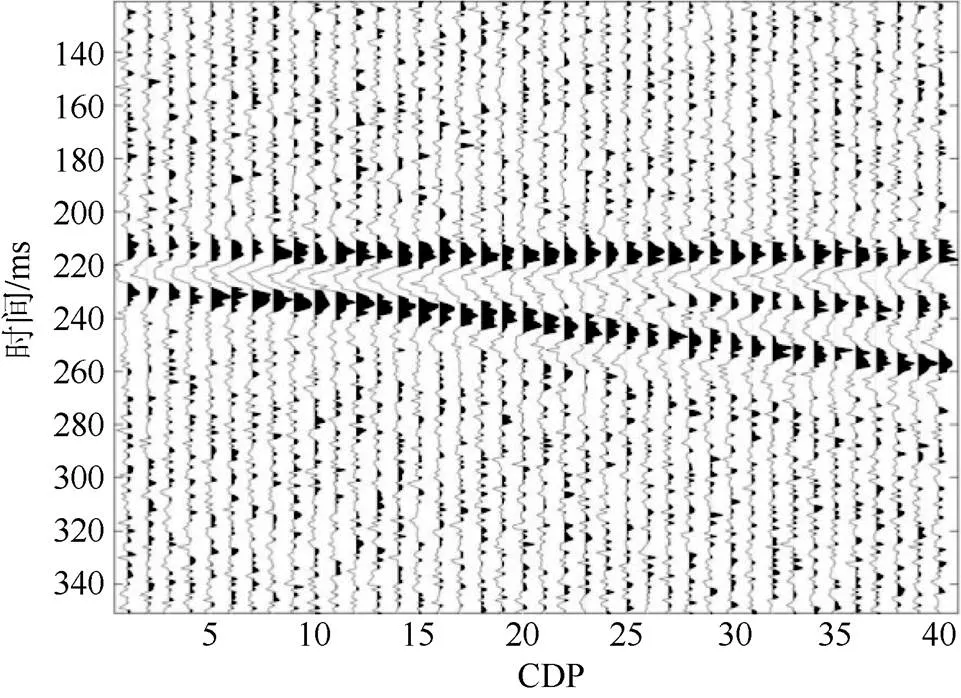
图4 增加噪声之后的楔形模型合成地震记录

上述实验结果表明，对地震数据进行VMD处理能有效降低噪声对煤厚预测结果的影响。利用VMD处理后的数据进行煤厚预测，其结果与实际煤厚具有较好的一致性，在煤层较薄时，预测结果更好。

3 实例分析

研究区隶属于鄂尔多斯盆地，区内主要可采煤层为6号煤层，位于石炭–二叠系太原组第二岩段上部，煤层厚度为7.04～20.77 m，平均12.70 m；可采区储量利用厚度为5.73～16.82 m，平均11.09 m，煤层厚度变化不大，利用VMD和SVM结合的方法进行该区的煤厚预测。图9所示为该研究区目的煤层原始地震数据记录与VMD去噪后的地震数据记录。图9a中原始地震数据记录的340～390 ms之间噪声比较多，360 ms 左右的同相轴不够清晰。与图9a对比可以看出，经过VMD去噪后，340 ms与390 ms左右的两条同相轴无明显变化，在360 ms左右的同相轴更为清晰，能量明显增强(图9b)。综上所述该研究区目的煤层响应特征良好。首先，在对三维地震资料进行VMD处理的基础上，提取振幅、瞬时频率和频带宽度地震属性，结果如图10所示。结合楔形模型的煤厚与振幅属性的关系，该区东北部和中下部振幅较强，煤层可能较薄；而西南部振幅较弱，工区中部有一斜条状振幅较低区域，该区域煤层可能较厚。而瞬时频率与频带宽度属性亦具有类似的特征，但各地震属性结果之间又具有一定的区别差异。单一地震属性结果反映了煤厚的可能分布特征，但其与煤层厚度具体数值之间对应关系不明确。

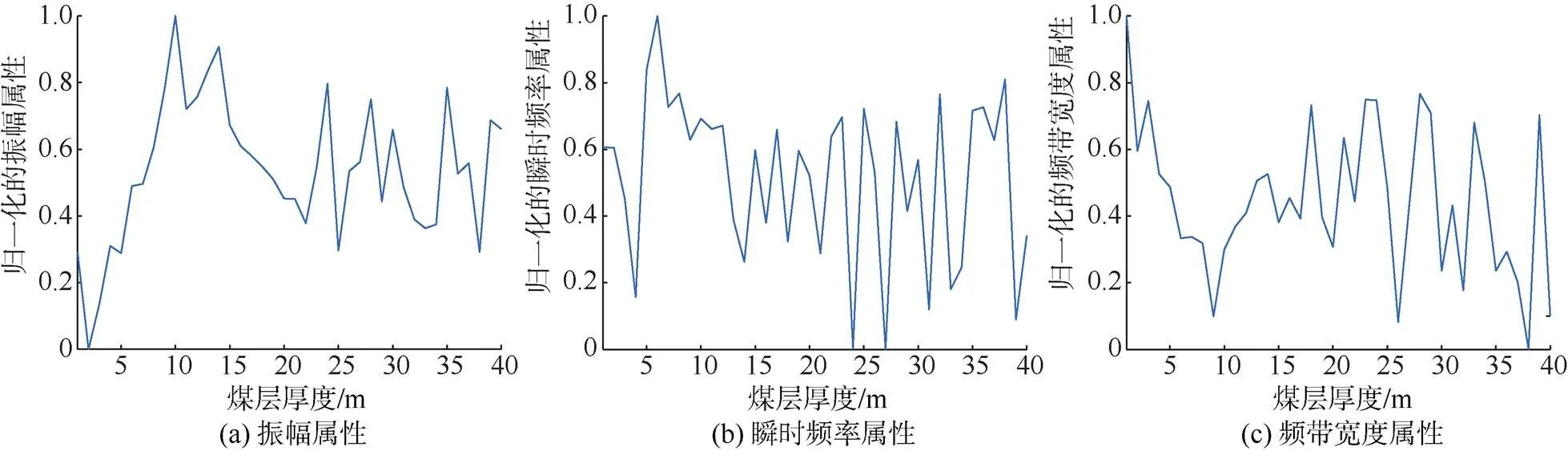
图5 含40 dB噪声楔形模型地震记录的地震属性

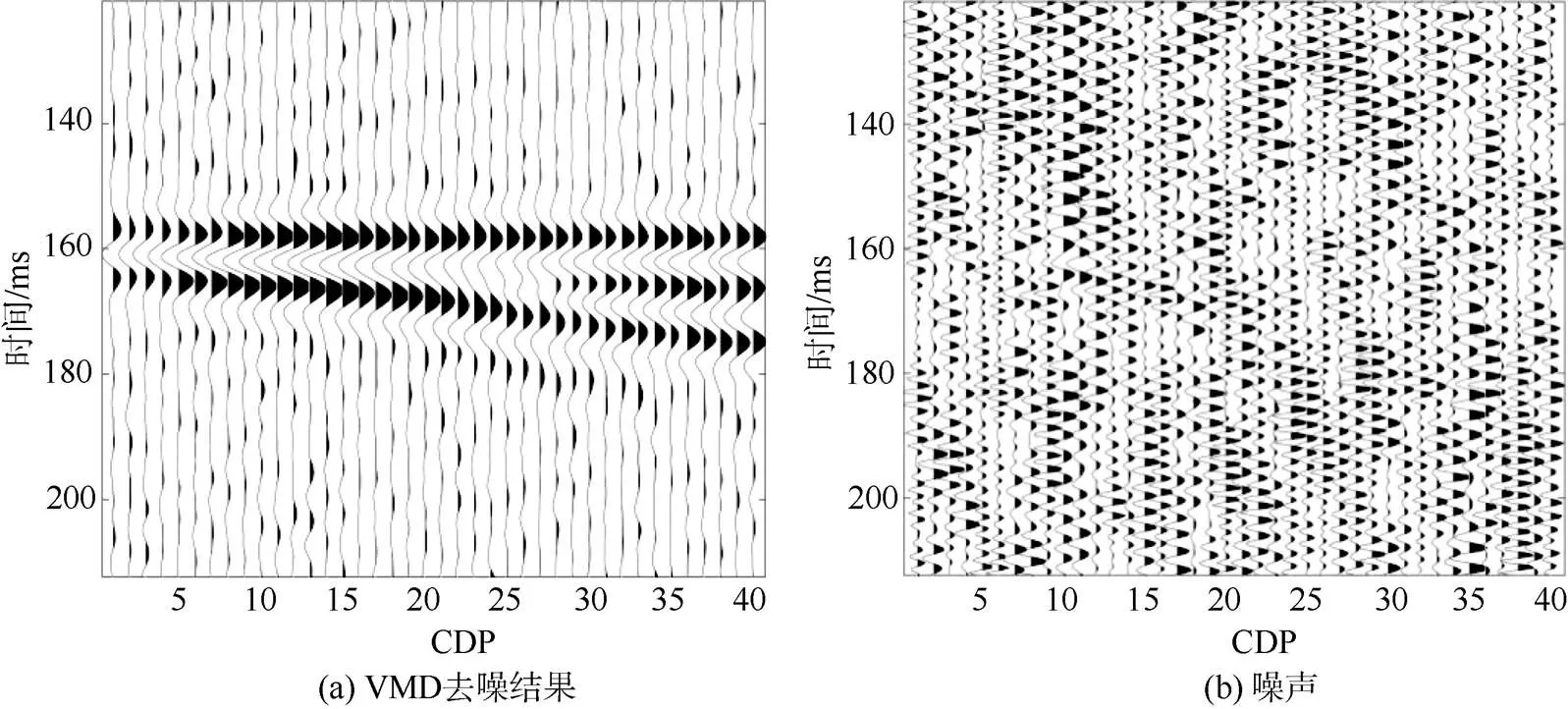
图6 含噪楔形模型合成地震记录的VMD去噪结果