2021年高考数学“开放性”数列问题探析及教学启示——以2021年全国数学理科甲卷第十八题为例

赵荣荣

(贵州省遵义市第一中学 贵州 遵义 563000)

2021年高考数学全国理科甲卷稳中求新，适度“开放”，聚焦学科素养，突出数学本质，注重关键能力，坚持开放创新。纵观2021年全国数学理科甲卷的诸多亮点与创新题型，最为“光鲜靓丽，夺人眼目”之一当数第十八题的“开放性”数列问题，该题型与地方卷及新高考对接，打破常规数列试题的考查方式，首次在旧版高考试题中考查“结构不良试题”，在适度开放创新方面表现非凡。该试题给考生充分的选择空间，是一道非常有特色的题目，对于没有接触过这类考题的考生来说是一个不小的挑战，让考生耳目一新的感觉，同时也暗含了高考对数学本质、数学概念、数学方法及核心素养的较高要求，克服“大量机械刷题”的刻板现象。

1.真题呈现

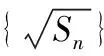
解析：若选择条件①②，则证明③成立

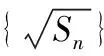
∴d=2a1,∴a2=a1+d=3a1，∴证明③成立

若选择条件①③，则证明②成立

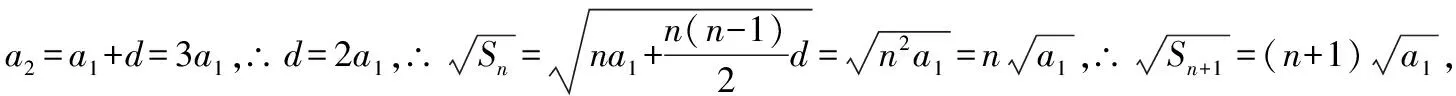
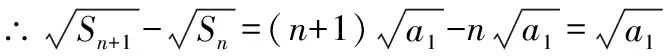
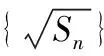
若选择条件②③，则证明①成立

当n≥2时，Sn-1=(n-1)2a1② ，由①②得：an=Sn-Sn-1=n2a1-(n-1)2a1=(2n-1)a1，当n=1时，a1=a1也符合该式。

∴an+1-an=(2n+1)a1-(2n-1)a1=2a1(为常数)n∈N* ∴数列{an}是以a1为首项，以2a1为公差的等差数列，∴证明①成立。

2.“开放性”数列问题这一新题型对教学启示

2.1 根据试题考查内容及形式确定教学侧重点。根据《普通高中数学课程标准(实验)》对数列部分的基本要求，学生能了解数列概念及表示方法；理解等差、等比数列的概念，掌握前n项和与通项公式。高考数列试题的设置基于课标基本要求，以数列概念、求通项公式、求前n项和这些基础知识与基本技能为考查热点，即注重“双基”的考查，起点相对不高。在考生达到基本要求之后，数列题目还关注知识的综合运用及同其他模块知识的融会贯通(例如同函数单调性、最值、周期性、不等式证明放缩法、数学归纳法、分析法等综合考查)。与此同时，数列问题还渗透着多种数学思想，如方程思想、函数思想、转化与化归思想、归纳推理思想等，考查学生综合能力素养。近些年，地方卷及新高考对开放创新思维的重视，“开放性”数列问题悄然而生，教学中在重点夯实数列相关概念等基础知识的同时，关注数列与其他模块知识之间的内在联系，点滴渗透，逐步拔高与巩固，通过对综合知识的运用和积累，提升学生数学思维能力，使学生具备良好的数学核心素养。重视以基础知识为依据，从多方位、多角度寻求解题方案，在练习中改编旧题目，创设“开放性”新情景，培养创新思维、发展创新能力。

2.2 根据考题要求确定数列课程教学模式。基于“开放性”数列问题的出现，如何有效挖掘学生的创造潜能，培养创新思维，发展创新能力，引导学生自主学习，提高学习效率，这一系列问题似乎成为应对和解决“开放性”问题探索和学习的关键。那么，课堂是学生学习的主要“载体”，建立有效的课堂教学模式，可以帮助我们切实解决这一系列困惑。

俗语说“心病”还需“心药”医，那么，“创新问题”也必然需要“创新课堂”才能“对症”解决。如今，翻转课堂这种教学模式已经颠覆了以往传统课堂对知识传授、知识内化的具体过程，学生变成知识的构建者，可以掌握学习的主动权。通过翻转课堂教学，学生需直接面对新情境、新问题和新内容，老师结合学生实际情况和能力设计详细导学案，引导学生自主探索、自主学习，多方位、多角度探究与思考。现以2021年全国数学理科甲卷18题为例，设计详细导学案：

(1)课前任务与问题：

(各小组课前分组准备，构建结构性知识，注重知识要点，课堂汇报)

任务一：请同学们思考等差数列的定义？如何判定或证明一个数列是等差数列呢？(包括文字描述、符号描述和注意要点)

任务二：等差数列的“灵魂”通项公式an等于什么呢？等差数列前n项和Sn的公式有哪几个？

任务三：有趣的“心连心”型，即已知Sn求an类型题目，我们之前是如何解决的呢？

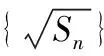
请同学们对新问题谈谈自己的感受与想法，如何解读新问题？有了新想法和新思路，请同学们动手实施自己的方案。任务五：设计一道变式，或查找资料，完成变式训练。

(2)课堂展示与分组讨论(合作交流)

活动一：展示与交流：(各小组展示题目及变式)

活动二：其他小组提问与质疑：(讨论)

试图从不同路径解决问题，集思广益，给学生“柳暗花明又一村”的感受。

活动三：对比与评估多种思维与方法，你觉得哪一种最适合你，谈谈你面对新问题的感受与解决新问题的“小经验”。

(3)收获与分享(点滴感受，心得，思维导图，小文章，设计变式题目)

整个设计流程，环环相扣，逐步引导学生从课前自主学习，到探究创新思考，课堂分组展示，再到课堂交流讨论，思维的碰撞，灵光的闪现，最后到收获与分享，做好知识自主学习与积极探索，充分调动学生主观能动性，切实有效开展课堂教学活动，达到教学目标。

2.3 根据“开放性”考题特点寻求考试对策。课堂教学的目的主要是为了帮助学生如何灵活应对纷繁复杂的考题。对于“开放性”数列新题型，同学们在系统学习与探索之后，需要总结出一套行之有效的考场策略。这类题目本身难度不大，但有一定的自主选择性，学生们处于青春期，生活和经验阅历尚且不足，面对诸多选择性问题总是“优柔寡断，难以抉择”。存在“选择困难”问题，不仅浪费大量考试时间，还会降低答题的信心，影响考试分数。还有部分同学选择了一种方案，进行不下去了，再回过头来，选择第二个方案重新开始解题，做了很多“无用功”，也大大浪费解题时间。面对的这样的状况，建议同学们在平时课堂训练多练习、多思考的同时，积累解题经验，考试时凭借解题经验准确解读条件和问题的深层含义，有效运用转化与化归思想。由深层含义找到解决问题最适合自己的切入点，由此“顺藤摸瓜”一步步得出问题的结论。试题另一个难点就是题目为字母化运算，相比数字化运算更为抽象，同时还要注意证明结果要替换掉中间变量，回归为题目已知量来进行表示。