基于模糊理论的井下漏电故障选线研究

胥 良，高建鑫

(黑龙江科技大学 电气与控制工程学院，哈尔滨150022)

0 引 言

中国煤矿井下供电系统普遍采用中性点不接地系统[1]，单相漏电故障是矿井下中性点不接地供电系统中最常见的故障[2]。当发生单相接地故障后，中性点偏移，非故障相电压会升高。若供电系统单相接地长时间运行，会影响供电系统运行的可靠性、安全性，甚至引发两点及多点接地故障，发生短路故障，造成煤尘与瓦斯爆炸等灾难性事故。因此，必须及时查找故障点并给予排除[3]。只使用一种故障检测方法具有很大的局限性，例如:零序过电流保护法对于电网干线漏电和由于电感器不平衡引起的漏电故障无法作出有效的区分[4];采用零序电压检测法容易受到系统电网电容的影响，不能准确测出系统电网对地的绝缘阻值[5]。该文利用模糊理论将多种方法进行融合，采用多判据选线方法进行线路故障测度计算，从而精确判断出故障线路。

1 基本理论

1.1 模糊选线原理

模糊选线原理主要用到的就是模糊理论，通过模糊理论来实现选线,通过事先选择的判定方法和规则来建立他们的故障测度以及权重系数的隶属度函数[6]。不同选线判据可能有不同选线结果,因为不同的判据所根据的是不同故障特征,不同的故障条件下故障特征表现程度不同[7-8]。当故障特征在某一判据下很明显时,应该更加重视这种判据,因此权重系数不是一个确定的数值，是随时变化的。最后融合每一个方法所提供的信息，得出判定结果。

1.2 故障测度和判据权重系数

在建立选线方法为数值型输出时，建立的方法可以计算出发生故障线路的故障特征某个度量，并且通过数值的方式输出出来。所以把在某一方法下测得的故障线路发生故障的概率叫作故障测度。采用综合选线的方法时，先要计算每一条线路在某一方法下的故障测度，通过对所选定的每种方法测得的故障测度求和，可以计算出这条线路总的故障测度值：

(1)

式中：μj为第j条馈线的故障测度；μij为在第i个方法下第j条线路故障测度；n为综合选线法中单一方法的个数。

权重系数是描述通过某一种方法来测某一条故障线路是否发生故障的正确程度。当发生一个故障时，使用一种方法来选线，然后分别建立故障测度和权重系数隶属度函数，从而求得多判据下每条出线的故障测度：

(2)

式中：μj为j条线路的故障测度；μij为第i个方法下第j号线的故障测度；ηi为第i个方法的权重系数；n为方法总数。

每条线路的故障测度都可以被求解出来使选线方法更加可靠，更加有利于故障的排除。

2 基于模糊理论的多判据综合选线

2.1 隶属函数的建立

该文选择零序电流群体比幅法、注入信号法以及零序电流基波比相法这3种单一选线方法，应用模糊理论融合3种选线方法，以提高选线的正确率。

2.1.1 零序电流群体比幅法

零序电流群体比幅法对供电系统接地方式的局限性比较大，这种方法更加适用于中性点不接地的供电系统，但对算法的要求和硬件、软件的要求比较低，选线的精度相对来说也比较高。在中性点不接地的供电系统中，故障线路与非故障线路的零序电流相量和相等。针对零序电流群体比幅法的隶属函数建立为

(3)

式中：x为各条出线零序电流幅值；I0，max为非故障线路的零序电流最大幅值；n是总线路条数。

故障线路与非故障线路的零序电流幅值差异越大，说明零序电流群体比幅法选线可信度越高，权重系数就越大，利用这种特点，建立权重系数隶属函数为

(4)

式中：I01和I02为所有线路中零序电流的最大值和第二大值，且I01>I02。

2.1.2 注入信号法

为了可以明显区分注入的信号和系统信号，与此同时还不能影响供电系统的运行，注入的信号选择的是一种频率及各次谐波频率与系统正常频率可以有效区分的电流信号。选用0.1 A的交流电流信号，频率为225 Hz，该信号能够很好地与系统正常电流区分并加以检测。建立注入信号法的隶属函数为

(5)

式中:x为检测元件检测出来的注入信号幅值。

当非故障线路检测到比较大的注入电流时，这种方法选线就会不可靠。因此，根据这一特点可以建立注入信号法权重系数的隶属函数为

(6)

式中：Imax为电流最大值；Isum为注入电流幅值的和。

2.1.3 零序电流基波比相法

为了得到一个关于零序电压和零序电流相位差在[0°,180°]上的单调函数，对φi(各条线路零序电流基波与零序电压基波的相位差)作如下变换：

(7)

φc,i∈[0°,180°]，φc,i越接近0°，对应的φi越接近90°(容性)，就说明第i号线路是故障线路的可能性就越小；φc,i越接近180°，对应的φi越接近-90°(感性)，就说明第i号线很有可能就是故障线路。因此可以定义零序电流基波比相法的故障测度隶属函数为

(8)

式中:max(φc，i)表示φc，i数组中的最大值。

在发生单相接地故障时，故障线路的零序电流基波相位和其他正常线路相反，此时该判据的可信度最高，应该使其判据权系数值为1。因此定义零序电流基波比相法判据权系数函数为

(9)

式中：Ln表示线路总数；Cn表示零序电流基波相位落在第三或第四象限内的线路数目。

2.2 模糊综合选线的实现

当系统有漏电故障发生时，首先检测零序电压的检测系统会判定有漏电故障发生，然后开始采集故障信号，利用上文对信号的处理运算，计算出带有数值的结果。通过下面的步骤可以计算出各条线路的故障测度：

1)分别计算出上述3种选线方法下的每一条线路的故障测度隶属度，最后将所计算结果建立一个模糊集：Ai={μi1,μi2,…,μin}，形成一个故障隶属度模糊矩阵：

2)计算出每一个单一判据的权重系数ηi，形成一个基于选线方法的权重集：

K=[η1η2η3]

3)结合2个矩阵可以得到加权后的故障隶属度模糊集，即

A′=K·A=[μ1μ2μ3…μn]

故计算出来的最大数值是故障线路的可能性极高，由于该结果的输出信息为数值型信息，所以其他数值较大的线路可以为其他线路是否故障起参考作用。

3 仿真分析

通过仿真软件建立一个电压等级为660 V的中性点不接地系统仿真模型，如图1所示。

图1 单相接地系统仿真图

该仿真模型中电缆都选用同一种电缆，长度分别设置为0.5、0.6、0.7、0.8和0.9 km，参数设置为r=0.17 Ω/km，L=0.34 mh/km，C=0.29 μF/km。图中注入的信号为幅值为0.1 A，频率为225 Hz的交流电流信号。

故障设置在线路L1的A相，位置为距离母线0.5 km处，故障开始时间为0.02 s，故障相角为0°，接地电阻50 Ω。

1)各线路的零序电流可以通过仿真测得。故障测度隶属度为

A1={1,0.09,0.09,0.011,0.013}

权重系数：η1=1。

2)故障发生后，经过大约0.2 s向系统A相中注入交流电流信号。可以明显检测出线路L1的注入电流信号幅值,如图2～6及表1所示。

图2 L1线路零序电流

图3 L2线路零序电流

图4 L3线路零序电流

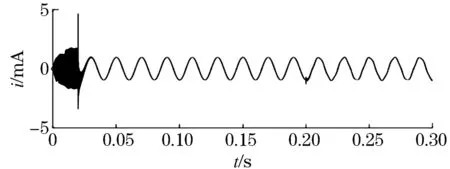
图5 L4线路零序电流

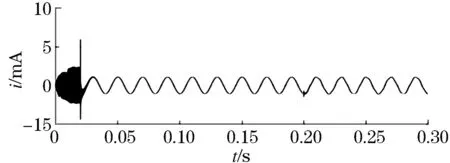
图6 L5线路零序电流

表1 各线路零序电流幅值

由仿真可计算出基于注入信号法选线的故障测度隶属度以及该方法的权重系数：故障测度隶属度为A2={1,0,0,0,0}，权重系数为η2=1。

3)由仿真可得各线路零序电流和零序电压的相位及相位差，可以得到基于零序电流基波比相法的故障测度隶属度以及该方法的权重系数：故障测度隶属度为A3={1,0,0,0,0}，权重系数为η3=1。

综合以上3种方法的故障分析，可得模糊矩阵A权重集K以及加权后的模糊集A′。仿真实验结果如表2所示。

模糊矩阵：

权重集：

K=[1 1 1]

加权后的模糊集：

A′=KA=[3 0.09 0.09 0.011 0.013]

表2 仿真实验结果

由加权后的模糊集即各线路的故障测度，可以得出线路L1为故障线路。

4 结 语

简要分析了零序电流群体比幅法、注入信号法和零序电流基波比相法，构造了一种基于模糊理论的多判据综合选线方法，克服了传统方法单一及判据存在局限性的问题。应用仿真软件在大量仿真基础上进行漏电故障分析，通过所述的方法去选线，仿真结果证明了运用这种方法可以准确选出故障线路。

在实际应用中，隶属度函数需要根据不同的实际情况来进行适当的调整，以保证隶属度函数可以更好地对应实际情况，更好地体现单一选线方法的优势，从而减少排除故障的时间。