规模化风电并网功率波动的预测及不确定估计研究

颜庆宇

(国网黑龙江省电力有限公司，哈尔滨 150090)

0 引 言

风力发电所占电源比重日益增大，在减少化石能源使用的同时也给电网的稳定运行带来一定冲击。电力系统要求在运行时保持功率的平衡，这就需要对风电功率和负荷功率的波动进行精准预测与快速响应。由此可见，在中国能源互联网建设中，如何最大限度地接纳风电等新能源电力，实现规模化风电等新能源电力的安全高效利用，是亟待解决的重大问题，也是能源互联网建设的核心。

由于风速的随机性和波动性，使得风速预测成为难题，特别是针对风速的不确定性分量进行预测亟待解决。短时预测功能一般可以预测未来数个时段的15 min级风电平均功率。与气象物理预测方法相比，短时预测方法一般根据风速、风向等历史信息，基于数理统计算法得到预测风速[1-6]，该方法预测精度随预测时段的延长下降较快，一般只用来获取未来数个时段风速或功率预测值。与目前风电确定性预测研究相比，不确定性预测研究相对较少。在风电不确定性预测研究方面，文献[7]针对短期风电功率时间序列，提出一类基于字典的系数编码预测方法；文献[8-9]将神经网络和平均影响值方法相结合，提出了一种神经网络平均影响值的超短期风电功率预测方法。

针对风速预测的不确定问题，利用三层小波分解方法与Mallat算法，提出融合数值天气预报方法，解决风速预测的难题。

1 原始风速的三层小波分解

1.1 多分辨分析

空间L2(R)上的多分辨分析是指构造该空间中的一组子空间{Vj}j∈Z，让其满足以下性质：

1)单调性：子空间存在着严格的包含关系

Vj⊂Vj+1,∀j∈Z

(1)

2)逼近性：

(2)

3)伸缩性：

φ(t)∈Vj⟺φ(2t)∈Vj-1

(3)

4)平移不变性：

φ(t)∈Vj⟺φ(t-k)∈Vj, ∀k∈Z

(4)

5)存在性：

存在φ(t)∈V0，使得{φ(2-jt-k)}k∈Z构成Vj的Riesz基。

定理：若{Vj}j∈Z是L2(R)上的一个多分辨分析，则存在唯一的函数φ(t)∈L2(R)，使得φj,k=2-j/2φ(2-jt-k),k∈Z为Vj内的一个标准正交基，其中φ(t)被称为尺度函数。

为了构造正交小波函数，特引入尺度函数。若φ(t)展成一个多分辨分析φ(t)∈V0，同时φ(t)∈V-1，{φ-1,k(t)}是V-1上的标准Riesz基，则φ(t)可由{φ-1,k(t)}表示，即：

(5)

单调性可将Vj用Vj+1和正交补来表示，即：

Vj=Vj+1⊕Wj+1

(6)

式中:Wj+1为子空间Vj+1的正交补空间;⊕为异或运算。

另外，让ψ(t)展成空间W0，ψj,k(t)展成Wj，{wj}j∈Z被称为小波空间，是相互正交的子空间序列。又ψ(t)可由V-1上的基表示:

(7)

以上方程即为尺度函数和小波函数的双尺度方程，小波函数和尺度函数的构造，可归结为系数{g(k)}k∈Z和{h(k)}k∈Z的设计。

1.2 Mallat算法

Mallat算法在原有金字塔算法的基础上，借鉴多分辨分析算法，构造了序列的金字塔式小波分解与重构算法。设序列f(t)在尺度空间Vj和小波空间Wj的投影为

(8)

不妨设cj,k=〈f(t),φj,k(t)〉，dj,k=〈f(t),φj,k(t)〉，由Vj=Vj+1⊕Wj+1，可得：

(9)

由尺度函数的双尺度方程可得：

(10)

由尺度函数正交性可得：

〈φj+1,n,φj,k〉=h(k-2n)

(11)

由小波函数双尺度方程可得：

〈ψj+1,n,φj,k〉=g(k-2n)

(12)

联立以上3个方程可得：

(13)

(14)

(15)

通过上面算法分析可知，将Vj空间剩余尺度函数cj,k进一步分解下去，可分别得到Vj+1、Wj+1空间的尺度系数cj+1,k和小波系数dj+1,k，同理分解下去，可以得到任意尺度空间，其分解过程见图1。重构过程其实是分解过程的逆过程，具体过程见图2。

图1 分解算法

图2 重构算法

2 风功率波动不确定性预测方法

2.1 融合数值天气预报方法

将Mallat算法应用到风功率波动不确定性分量的预测，建立了融合数值天气预报(numerical weather prediction，NWP)方法。

通过使用Mallat小波分解算法，对某风电场2019年5月至7月的风速数据每10 min(如图3所示)进行分解。图4是原始风速经过三层小波分解后得到的结果。将原始的风速序列分解为不同频率的子序列后，就可以针对每个子序列建立统计预报模型。

图3 风速实测数据

图4 三分小波分解后数据

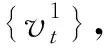
利用经典的Pearson自相关函数法来考察时间序列的自相关性。设{xt}t=n(n=1,2,3,…)是一随机时间序列，则样本xt与k个步长后的样本xt+k之间的自相关系数被定义为协方差：

(16)

图5 相关长度变化曲线

图6 自相关系数达到0.8的相关长度

当自相关函数值大于等于0.8时，数据之间存在很强的关联，即可认为自相关函数值大于0.8时所对应的相关长度内的预报结果可信度较高，所对应的相关长度即是可预报时长，即预报的结果可信度较高。

自相关函数值小于0.8时，数据之间的相关性不强，所对应的相关长度内的风速预报结果的可信度较低，所以取自相关函数值大于等于0.8以上的相关长度作为可预报时长。

对于每一频率分量上建立的统计预报模型，各分量多步预报的自相关长度分别取为4 h、1 h、0.4 h、0.2 h。每一层中，设L为该层的自相关长度，则当前时刻和L-1时刻的风速作为该层统计预报模型的输入值。

得到各层的预报结果以后，利用Mallat小波重构算法对每个尺度上的预报结果按照相应的预报时间进行合成。每层分量只在其相应的时间区间内进行预测，即高频分量负责0.2 h区间的预报，低频分量负责1 h区间的预报，其它分量依次类推。

2.2 统计模型与NWP融合算法

由NWP和实测数据的信息有效性分析可以看出，利用统计模型进行风速预报时，当预报时间超过4 h后，低频分量的自相关性函数值低于0.8，并随着预报时间的增加而降低，因此预报结果的可信度开始降低。而NWP的预报能力较强，但是瞬时预报效果差。所以，将统计模型和NWP进行融合的思路是4 h以内风速预报可从NWP和历史风速中获得有效信息。

将NWP模型的预报结果和统计预报模型的预报结果进行加权，得到日前风功率融合预报模型如下：

v=w1v1+w2v2

(17)

式中：v为最终的日前风速预报结果，v1、v2分别为统计预报模型及NWP模型的风速预报结果；w1、w2为融合加权时v1、v2对应的权值，其中在4 h内合成时，w1、w2由遗传算法得到，而4～24 h的合成时w1=0，w2=1，即4 h内的风速预报结果由统计预报模型和NWP模型的预报结果合成得到，而4～24 h的风速预报结果仅由NWP模型得到。

3 仿真计算

3.1 NWP算法与SVM算法对比

风功率预测方法与原有算法效果对比如图7～8所示。

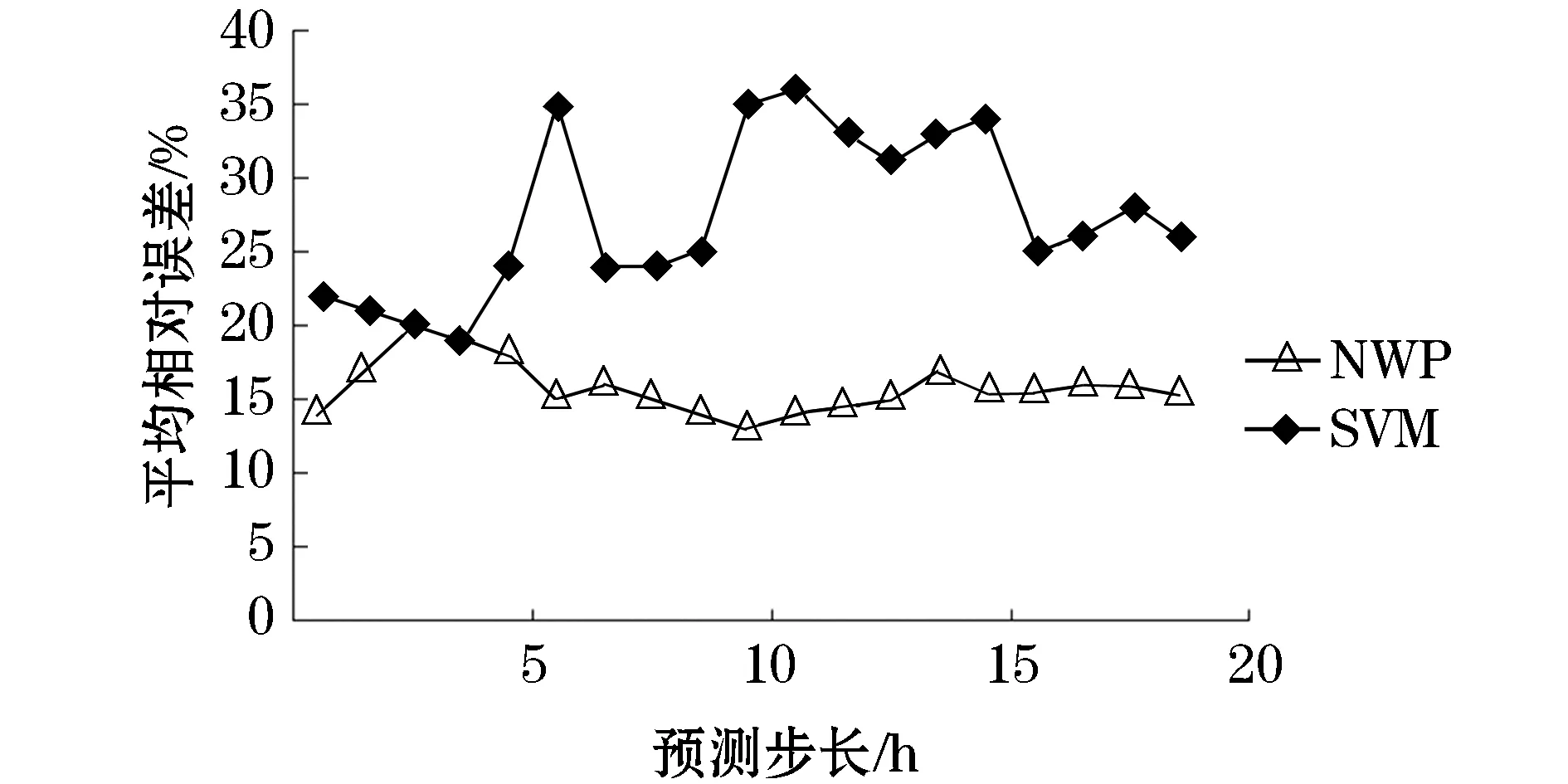
图7 统计预报模型

图8 数值天气预报模型

NWP目前普遍采用典型WRFa预报模式，为三层嵌套网格，计算网格分别为：27 km×27 km，9 km×9 km，3 km×3 km。NWP的计算原理，决定其只含有长周期分量而不含有短周期湍流分量且计算结果输出步长为1 h时的瞬时预报结果差。

支持向量机(support vector machine, SVM)是统计预报模型的一种。采用SVM和NWP预报风速时，通过对预报结果的平均相对误差和均方根误差曲线进行分析，可以看出，当预报时间在4 h以内时，NWP的预报结果与SVM的预报结果相差不大，但是一旦预报时间超过4 h后，不管是平均相对误差还是均方根误差，NWP的预报结果都要远远好于SVM的预报结果。

3.2 日前风动率预测

将提出的风功率波动不确定性预测方法应用到日前风速预测。

图9是融合NWP的日前风速多步预报方法得到的日前风速序列曲线与实测的风速序列曲线的对比图。可以看出，预报风速与实测风速的吻合度较高，表明提出的风速预测方法精度很高。

图9 风速预测

从图10可以看出，融合NWP的多尺度预测方法平均相对误差分布在10%～15%之间，而不融合NWP的统计预测误差分布在25%～35%之间，融合NWP的多尺度预测方法预测精度较高。

图10 平均相对误差

4 结 语

基于三层小波分解与Mallat算法提出了风功率的数值天气预报算法，该算法有效解决了大于4 h的风速预测精度问题；同时考虑数值天气预报算法在小于4 h的预测精度较低，采取了统计预报模型和数值天气预报模型相结合的融合NWP多尺度预测方法。采用融合NWP多尺度预测方法进行日前风速预测，结果表明,预测风速与实测风速曲线高度吻合，同时融合NWP的多尺度预测方法精度要远远好于不融合NWP的统计预测方法。