基于ARMA模型的故意伤害案件预测模型研究

曹 霁

（南京森林警察学院基础部，江苏 南京 210000）

一、研究背景

伴随着大数据时代的到来，全国各级公安机关系统都已基本建立较为完备的犯罪事件数据库，各类犯罪事件的发生情况和相关信息都记录在内。但目前关于这些数据更多集中在简单的应用，如查询、统计和简单的分析等。随着社会形势和科技的快速发展，公安机关对犯罪行为的治理早已不仅仅只局限于“治理”，对犯罪现象进行系统研究，“预防”犯罪行为的产生更是公安机关的迫切需要。如何利用这些已有的数据，通过对过去犯罪数据的分析，预测未来一段时期内犯罪事件类型、数量的变化情况，从而为警力配置和犯罪事件的预防提供科学的参考依据，以便更加充分地利用有限的警力资源提高出警效率、精准打击犯罪行为，更好地保护人民群众的生命和财产安全，都是非常有必要和意义来进行研究的。

时间序列分析是概率统计学科中应用性较广的一个分支，它广泛应用于金融经济、气象水文、信号处理、机械振动等实际问题中，是一个具有相当高的实用价值的应用研究领域。时间序列分析能够充分利用原时间序列的各项数据，运算速度快，对模型参数有动态确定的能力，是一种非常好的短期预测方法。［1］所谓的时间序列，指的是同一种现象在不同时间上的相继观察值排列而成的一组数字序列。观察这组时间序列在过去的变化规律，推断其以后可能的变化趋势，从而对该现象的未来进行预测，就是时间序列分析法。

近年来有关时间序列分析在公安数据处理中的主要研究主要分为如下三个方面：

（一）从社会犯罪的特征出发，探讨社会犯罪统计的意义，讨论犯罪时间序列分析的意义与方法，提出这一领域的研究方向。代表性论文为国务院特殊津贴享有者、辽宁警察学院何平教授的《关于社会犯罪统计理论与时间序列分析的研究》。该论文为何平教授在意大利佛罗伦萨大学讲学的内容节选，详细系统地讲述了犯罪统计学理论的理论来源和特点，并对犯罪时间序列分析的研究进行了展望。［2］

（二）利用时间序列分析对具体案件类型的增长趋势进行预测。如同济大学法学院单勇、阮重骏发表的《基于X11方法的盗窃犯罪时间序列分析》，发现了温州市龙湾区的盗窃类犯罪的时间分布规律与季节变化；由国家“十二五”科技支撑计划项目资助的，中国人民公安大学的陈鹏、赵鹏、瞿珂的《基于时间序列模型的110警情数据预测研究》；沈齐、范馨月在中国刑警学院学报上发表的《季节性ARIMA接警量预测模型在警情分析中的应用》；浙江警察学院教师韩一士、范英盛、李国军、郑滋椀的《基于ARIMA模型的通讯网络诈骗犯罪增长趋势分析——以浙江省衢州市为例》；湖南大学法学院屈茂辉、郝士铭《基于ARMA模型的我国财产类犯罪人数预测研究》等等。

（三）通过改进时间序列模型或者利用更加先进的统计分析软件来更加精确地预测犯罪态势。例如北京工业大学的黄娜、何泾沙、孙靖超、朱娜斐的《基于改进LSTM网络的犯罪态势预测方法》；南京审计大学钟飚、袁梦佳发表在中国人民公安大学学报（自然科学版）上的《犯罪时间序列预测分析方法研究——以CrimeStat软件为例》；武汉大学涂小萌、陈强国发表在北大核心期刊电子技术应用上的《基于ARIMA-LSSVM混合模型的犯罪时间序列预测》；上海交通大学曾伟华的硕士论文《基于ARMA模型的犯罪事件预测分析系统的设计与实现》等等。［3］

目前，利用时间序列分析的方法在公安数据处理方面的应用的研究趋势是充分利用已有的数据，通过改进算法，采用更加先进的数据处理手段，更准确、更有效、误差性更小地预测犯罪发展趋势。下面以故意伤害案件为例，在《中国第三产业统计年鉴》上我们可以查到2006—2019年公安机关受理故意伤害案件数，2020年的数据尚未查到，我们将在这些历史数据的基础上，构建ARMA模型，并对2020—2025年的公安机关受理故意伤害案件数进行预测。

二、ARMA模型

ARMA模型即自回归滑动平均模型，它是模型参量法高分辨率谱分析方法之一。这种方法是研究平稳随机过程有理谱的典型方法，是研究时间序列的重要方法。［4］由自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础“混合”构成。但它比AR模型法与MA模型法有较精确的谱估计及较优良的谱分辨率性能，但其参数估算比较繁琐。在市场研究中常用于长期追踪资料的研究，如：Panel研究中，用于消费行为模式变迁研究；在零售研究中，用于具有季节变动特征的销售量、市场规模的预测等。

ARMA模型参数估计的方法很多。如果模型的输入序列{u（n）}与输出序列{a（n）}均能被测量时，则可以用最小二乘法估计其模型参数，这种估计是线性估计，模型参数能以足够的精度估计出来。

许多谱估计中，仅能得到模型的输出序列{x（n）}，这时，参数估计是非线性的，难以求得ARMA模型参数的准确估值。［5］从理论上推出了一些ARMA模型参数的最佳估计方法，但它们存在计算量大和不能保证收敛的缺点。因此工程上提出次最佳方法，即分别估计AR和MA参数，而不像最佳参数估计中那样同时估计AR和MA参数，从而使计算量大大减少。

所谓的ARMA（p，q）序列指的是：设{Xt，t=0，±1，±2，…}是零均值平稳序列，若满足，其中为零均值、方差为的平稳白噪声，则称为阶数p，q的自回归移动平均序列，简称ARMA（p，q）序列。接下来我们将逐步完成ARMA模型的构建及预报，先开始检测序列的平稳性。［7］

三、平稳性Daniel检验

一个平稳的时间序列可以极大地减少需要分析的随机变量的个数，并相对增加了待估参数的样本容量，达到降低分析难度和提高估计精度的目的。检验序列平稳性的方法很多，在这里我们采用Daniel检验。

假设时间序列样本为 χ1，χ2，…χn，其顺序统计量为χ(1)，χ(2)，…χ(n)，若χi=χ(k)，则称Ri=k为χi在样本中的秩。对于二维变量 (t，Rt)，t=1，2，…，n计算其Spearman相关系数，并构造统计量。作假设检验如下：

H0：序列Xt平稳；H1：序列Xt非平稳。

四、模型识别与定阶

在该部分，我们将利用AIC准则，判断该序列是属于AR（p）、MA（q），或者ARMA（p，q）模型，并确定阶数 p，q。［6］

表1 AIC值结果

比较可得当p=2，q=2，时，AIC值最小，因此我们选用ARMA（2，2）模型进行拟合。利用MATLAB软件建立模型并进行预测，得到的模型为。

五、模型检验与预测

利用MATLAB中的lbqtest程序对拟合残差进行Ljung-Box检验，检验结果h=0，说明残差序列为白噪声序列，不存在还未提取的信息，模型通过检验。

对已知数据上述预测模型的相对误差，见表2。

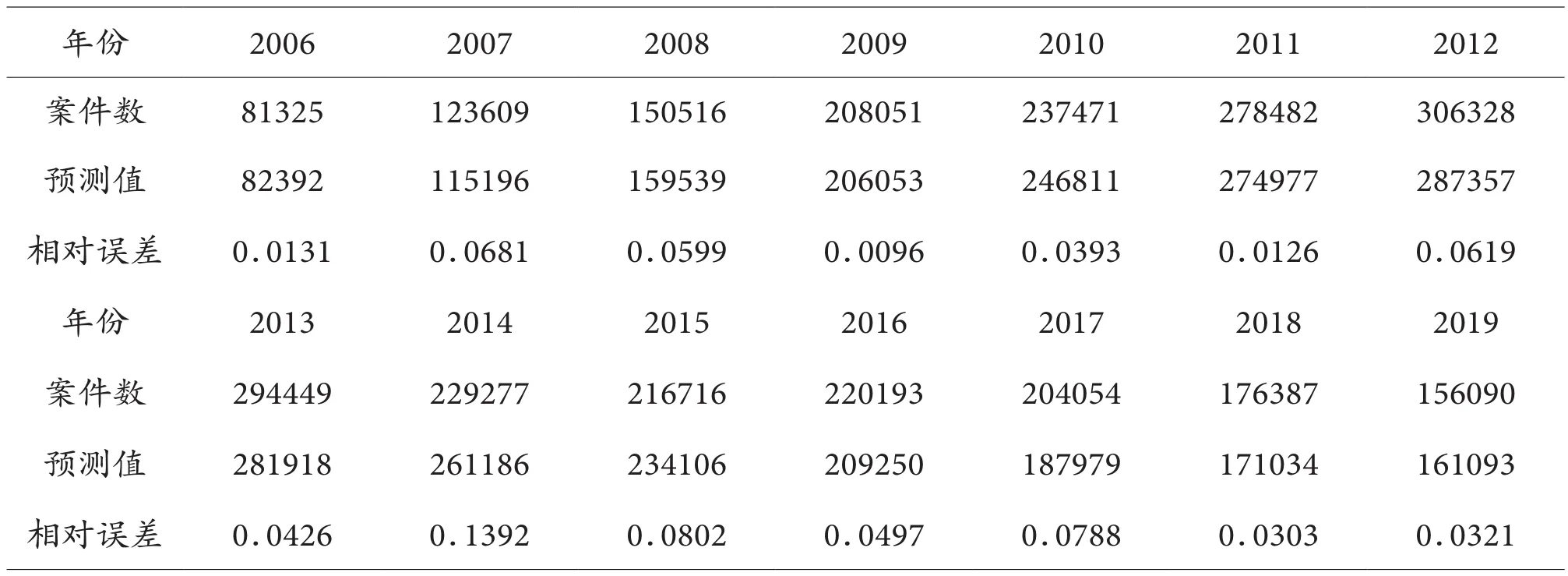
表2 模型检验结果

可以看出该模型的预测精度是较高的。

利用forecast程序预测未来五年公安机关受理故意伤害案件数亿次，见表3。

表3 预测结果

六、总结

时间序列分析是定量预测方法之一。它包括一般统计分析（如自相关分析，谱分析等），统计模型的建立与推断，以及关于时间序列的最优预测、控制与滤波等内容。经典的统计分析都假定数据序列具有独立性，而时间序列分析则侧重研究数据序列的互相依赖关系。后者实际上是对离散指标的随机过程的统计分析，所以又可看作是随机过程统计的一个组成部分。它可以在充分利用历史数据的基础上，简单、快速地预测在未来较短时间内数据的变化趋势，预测精度高，便于掌握，具有非常广泛的应用领域。

根据过去几年公安机关受理的故意伤害案件数，利用时间序列分析来预测未来几年公安机关受理故意伤害案件数，可以协助公安机关制定更加有效的犯罪防范对策，有效防范相关犯罪行为的发生，这是一件非常有意义的工作。