同轴等大圆线圈互感系数的测量

隗群梅

摘  要：同轴线圈的互感系数与其相互作用能和相互作用力密切相关，是物理学的基础理论问题，也具有工程应用价值。该文采用LCR数字电桥先测量线圈N1和N2的自感LN1和LN2;然后根据自感和互感的关系，得到不同距离处的互感系数M;最后利用Origin8.0强大的数据处理功能模拟出互感系数与相对位置之间的关系表达式，实验数据曲线与拟合曲线拟合系数达到99%以上，与理论积分近似计算的结果表述一致。实验测量互感的方法可以减少繁琐的积分计算，也可以得到互感系数与相对位置之间的函数关系。

关键词：LCR数字电桥 自感 互感系数 Origin程序 相对位置

中图分类号：O441 文献标识码：A   文章编号：1672-3791（2021）10（b）-0000-00

Mutual Inductance Measurement of Coaxial and Large Round Coils

WEI Qunmei

（College of Science， China University of Petroleum （east China）， Qingdao， Shandong Province， 266580 China）

Abstract： The mutual inductance of the T coaxial coil is closely related to its interaction energy and force. It is a basic theoretical problem of physics and has engineering application value. In this paper， the LCR digital bridge is used to measure the self-inductances LN1 and LN2 of the coils N1 and N2; then， according to the relationship between self-inductance and mutual inductance， the mutual inductance coefficient M at different distances is obtained; finally， the powerful data processing function of Origin8.0 is used to simulate the mutual inductance The relationship expression between the coefficient and the relative position， the fitting coefficient of the experimental data curve and the fitting curve reaches more than 99%， which is consistent with the result of the theoretical integral approximate calculation. The method of experimental measurement of mutual inductance can reduce the tedious integral calculation， and can also obtain the functional relationship between the mutual inductance coefficient and the relative position.

Key Words： LCR digital bridge;Self-inductance; Mutual inductance coefficient; Origin program; Relative position

兩个同轴圆线圈互感系数是电磁学的基础理论问题之一，在理论上进行推导时都需要进行适当的近似或猜想才能得出近似的解析公式[1-4]，且其在进行计算时一般都比较复杂，因此常用实验的方法进行测定[5-6]。下面根据电感和互感的关系，得出互感系数的表达式，从表达式中可以看出，只需要借用现在功能全、测量精度高的LCR电桥测量自感和互感系数[7]，就可以得到互感系数与线圈距离数据关系，再利用Origin8.0[8]强大的数据处理功能建立两固定线圈的互感系数与其相对位置的关系表达式，并与参考文献[1-3]中理论计算比较，得出实验测量得到的解析式与理论计算的结果变化规律一致，且数据曲线与拟合曲线的拟合系数达到99%以上。由此可见实验测量互感系数的也可以被工程技术所运用。

1 两线圈互感系数M的测量原理

根据电感和互感的关系，可根据同名端的顺向串联和反向串联值计算得到互感值。设线圈N1、N2对应的自感为LN1、LN2，则顺向串联的电感值L1=LN1+LN2+2M。反向串联时电感值L2= LN1+LN2-2M。从而可得到

M=1/4 |L_1-L_2 | （1）

对于铁芯线圈，耦合程度紧密，所以M值相对比较大;对于两个空心线圈，互感系数只与两个线圈回路本身结构和相对位置有关，而与电流无关[9]。

2 判断互感线圈同名端的方法

如图1所示，将两个绕组N1和N2的任意两端（如1、3端）连在一起，用LCR测试仪测量电感值得到L1;再将两个绕组N1的1端和N2的另一端4端连在一起，如图2所示，用LCR测试仪测量电感值得到L2;如果L1>L2，则1、4为同名端，2、3为同名端;如果L2>L1，则1、3为同名端，2、4为同名端。

3 两线圈互感系数M的测定

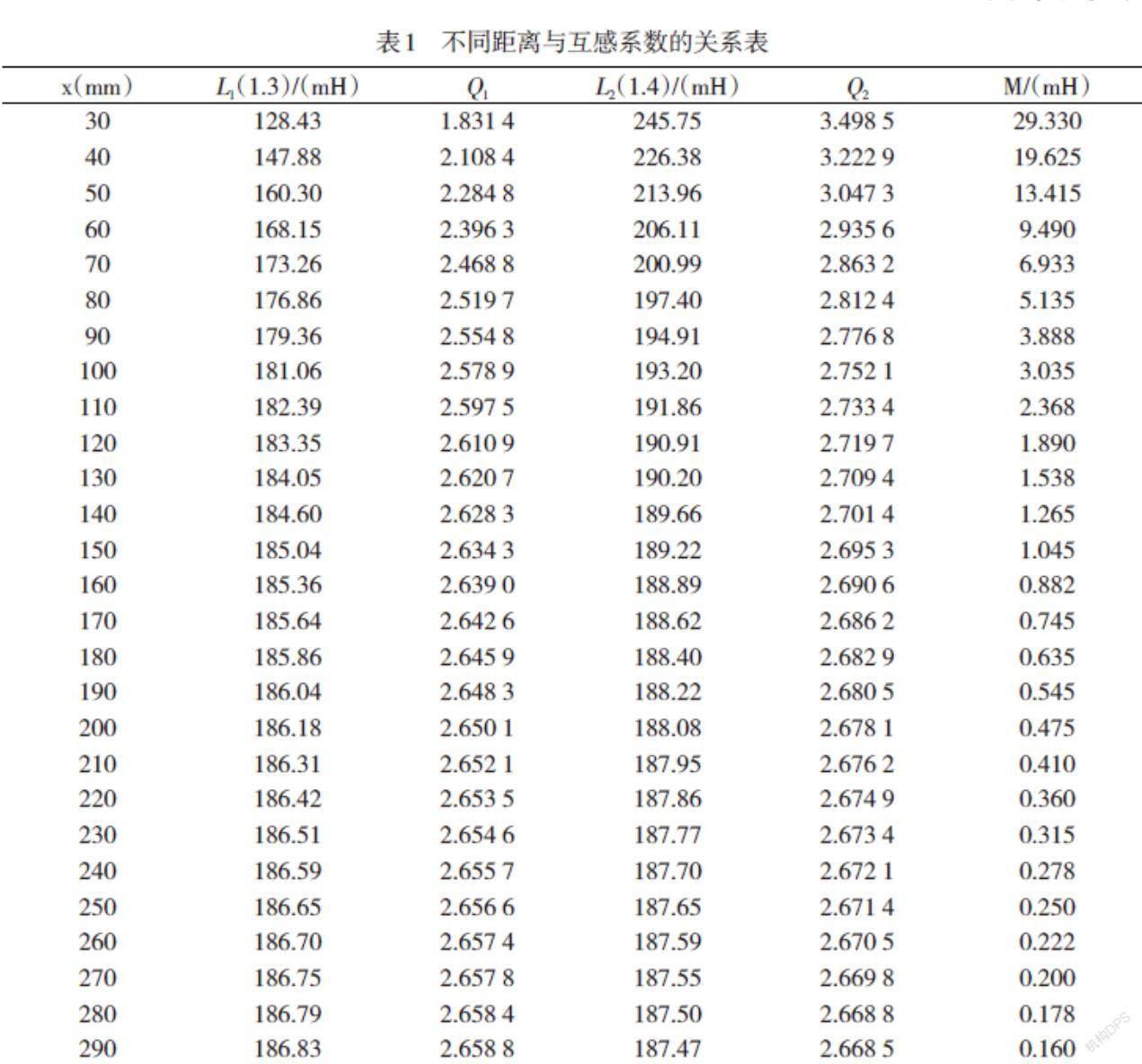
按照图1和图2连接线路，测量的相关数据如表1。从表1中可得出：L2>L1，则1、3为同名端，2、4为同名端，L1为反向串联电感值，L2为顺向串联电感值，则互感系数表达式为：

M=（ L2- L1）/4   M=□（（L_2-L_1）/4）     （2）

根据式（2），计算的互感系数数据如表1。

根据表1，利用Origin8.0做出图形，如图3。

利用Origin8.0对图3拟合结果可以得出两共轴线圈的互感系数与相对距离关系表达式为：

M=57.35/（1+（x/30.7 ）^2.4 ）-0.1544   （3）

拟合曲线相关系数为R2=0.99995，完全重合，非常完美。由Origin8.0拟合得到互感系数与相对距离关系式（3）与文献[4]中由“数值计算和曲线拟合的方法”得到了共轴等大圆线圈间互感系数的结果近似。

3 结语

同轴线圈的相互作用能和相互作用力都与互感系数密切相关，对于其值的计算或者测量就会直接影响到相应的同轴线圈的工程应用，而互感系数的计算需要先利用毕奥-萨伐尔定律导出的互感系数积分公式，再进行数值计算，积分计算过程繁琐，计算量大。因此通常用实验的方法测定，常用实验方法有：暂态法、磁通法、伏安法、串联法等，这些方法在测量互感系数时，有些测量要求比较高、有些计算量比较大，都不够理想。该文利用LCR数字电桥测量出同名端的顺向串联和反向串联值可以计算出互感系数，这种方法相对来说测量操作简单，且随着现代科技的发展，实验仪器测量精度不断提高，实验方法不断优化，实验测量得到的结果也越来越接近理论值。Origin8.0强大的数据处理功能也被运用到两共轴线圈的互感系数与相对距离函数关系式的建立中，且得到的结果与计算得到的变化规律一致。实验测量互感系数的方法与电脑程序运用将会被更广泛的运用。

参考文献

[1] 张伟，陈俊斌.同轴等大线圈互感系数及相互作用力的近似解析公式[J].大学物理，2004（8）：36-37，40.

[2] 龚禔.一般情况下两共轴圆线圈间互感系数的简便计算[J].大学物理，2011，30（4）：46-48.

[3] 熊慧，刘来，刘近贞.任意空间位置下改进的互感系数计算方法[J].传感器世界，2018，24（6）：7-11.

[4] 张若舟，秦明阳，张露，等.超导薄膜磁场穿透深度的双线圈互感测量[J].物理学报，2020，69（4）：249-258.

[5] 王鹏.通电直螺线管自感与互感的物理图像[J].物理通报，2021（7）：39-42.

[6] 周群益，莫云飛，侯兆阳，等.两共轴环电流之间的互感系数和作用力[J].大学物理，2020，39（10）：5-11.

[7] 范宜标，陈晶晶，林炳辉.基于自由轴法便携式LCR测试仪的设计与实现[J].黑河学院学报，2018，9（11）：210-212.

[8] 王环江，吴怡逸，肖寒，等.Origin8.0用于物理化学实验数据拟合处理[J].山东化工，2020，49（9）：218-221，228.

[9] 岑敏锐.同轴等大方形线圈的互感系数[J].武汉工程大学学报，2007（4）：90-92.