带有电压补偿的改进I—V下垂控制策略

薛阳，华茜，叶晓康，李蕊，孙越

（上海电力大学自动化工程学院，上海 200090）

随着当前化石燃料的减少和环境污染日益加重等问题，可持续发展的理念受到重视，为了对诸如光伏、风电等分布式能源的有效控制，微电网具有广阔的发展前景，它是分布式电源（distributed generation，DG）、储能系统（energy storage system，ESS）以及负荷的系统整合，是一种小型的发、配电系统，并且采用电力电子变换器进行能量控制、管理及优化，为可再生能源整合到电网中提供了解决方案，其具有独立和并网2种运行模式。根据系统结构、电源等要求的不同，可大致分为交、直流两大类微电网系统[1-3]。直流微电网存在较少的能量变换过程，也无频率、相位和无功功率控制等问题，且分布式电源和储能环节的供电形势大多为直流，对于一些重要负荷（飞机、电动汽车、数据中心、船舶等）来说，它是有效的供电电源，当前许多家用电器都存在直流供电形式，因此直流微电网控制可靠性高、结构简单、供电方便等一些优势日渐突出，得到了专家和学者的广泛关注和认可[4-6]。

独立直流微电网的控制模式有集中式和分散自治式2种，其中前者主要依靠顶层的中央控制器发出每个变换器的输出命令，经过线路通信后到达底层对每个变换器进行控制，其可靠性较低；而后者无需中央控制器和通信技术即可实现对电压、功率等参数的调整，其可靠性较高，可以即插即用[7]。分散自治式在任何一种运行模式、且在无需改变下垂控制策略的情况下，可以实现运行状态的切换[8]。因此，国内外学者研究应用最为广泛的分散式控制是下垂控制[9-11]。

下垂控制是根据直流母线电压来调整变换器的输出电流值，进而更好地控制直流母线电压，自从应用于微电网中以来，已有广泛的讨论及研究。目前文献对V—I型下垂控制的研究较为成熟，是通过检测变换器的输出电流来调节电压外环的参考电压值，再通过电压外环、电流内环调节变换器的输出电压值[12]。由于传统控制方法存在局限性，因此对改进控制方法是研究热点。文献[13-14]通过添加虚拟电阻来实现并联变换器之间电流分配，并且不需要进行通信。文献[15]利用“电流-电压变化率”的关系来降低电压与电流间的耦合，这种新型控制策略可以提高电流分配精度来稳定输出电压，但依旧存在母线电压偏差。文献[16]采用了动态虚拟阻抗使下垂系数能够自适应调整，减小母线电压降落。文献[17]建立下垂控制适用于多储能换流器并联的直流微电网的等效模型，提出了分级稳定控制方法。文献[18]提出的自适应下垂控制策略可以满足电流分配和母线电压要求，但是会出现通信延迟的缺陷。也有文献对I—V型下垂控制进行了研究。文献[19]采用I—V下垂控制策略，通过与虚拟阻抗的数学关系得到参考电流值。文献[20]对两种下垂控制进行了对比，相比于V—I型控制，I—V型控制策略可以减少一个PI控制器，对此分别建立相应的模型，分析了动态特性，经过分析后得出I—V型下垂控制的响应速度比V—I型快。文献[21]对多变换器进行建模，并且分析了动态特性，改善了输出电流和母线电压的恢复时间和响应速度，但是依然存在电压降落。

为了进一步改善电流分配精度和减小母线电压降落，本文在分析直流微电网的典型结构和对传统V—I下垂控制的基础上，提出一种直流微电网改进补偿型I—V控制策略，建立I—V控制模型并加入补偿环节。对于电压降落的问题，本文提出母线电压无偏差控制策略，设定适合的收敛系数，利用上移补偿使母线电压保持在额定值。最后通过仿真实验，验证了所提改进理论方法的有效性和优越性。

1 直流微电网与传统下垂控制策略

1.1 直流微电网结构与特点

典型的直流微电网是一个多源、多负荷的系统，系统结构如图1所示，每个部分都是通过对应的变换器并联到直流母线上。其中以光伏、风力发电机为主的分布式电源的作用主要是实现低碳发电，功率传递方向为单向；混合储能系统包括能量型储能元件（蓄电池）和功率型储能元件（超级电容），可以双向传输功率，对电源及负荷所产生的功率波动有一定平抑作用，对分布式发电的随机性和间歇性也有一定补偿效果；本地负荷只作为消耗能量的单元，功率为单向传输。直流微电网系统可以独立与并网运行，如果需要与外界交流大电网互联，则需通过双向DC/AC变换器接到交流大电网中。

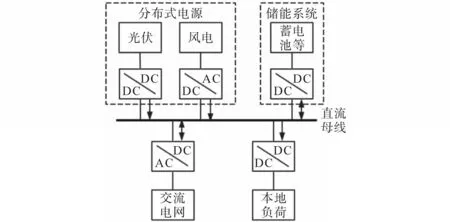
图1 直流微电网典型结构图Fig.1 Typical structure diagram of DC microgrid

1.2 传统下垂控制策略

目前直流微电网中较为常用的下垂控制方法为“电压—电流”（V—I）型控制，其特性可以用下式表示：

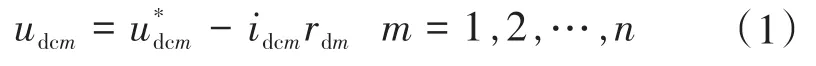
式中：udcm为第m组DG的实际输出电压值；u*dcm为第m组DG的变换器输出侧电压给定值；idcm为第m组DG的变换器输出电流值；rdm为第m组DG的下垂电阻系数的等效阻抗值。

图2为含有两组DG并联的直流微电网系统简化电路模型，其中rlinei(i=1,2）为直流母线与相应DG间的线路阻抗值；idci为相应DG的输出电流值；rload为微电网等效公共负荷阻抗值；upcc为公共直流母线的电压值；iload为公共负荷电流值。

图2 典型直流微电网简化模型图Fig.2 Simplified model of typical DC microgrid

根据图2电路简化模型可以得到第i组DG的输出电流表达式为

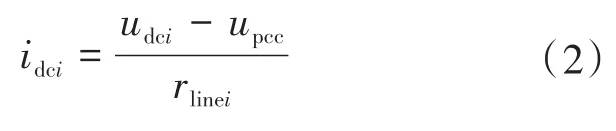
线路阻抗rlinei的存在会影响电压与电流的分配情况。在规模较小的直流微网中，当rlinei远小于rdi的情况下，线路阻抗的影响可以被忽略，则输出电流和下垂系数成反比关系。而实际情况中，若直流微电网的规模较大，线路阻抗rlinei也较大，且不能忽略，两组DG输出电流的比例关系为

图3为传统下垂控制示意图，其中，实线表示下垂特性曲线，虚线表示输电线路电压与电流的关系，当两组DG输出功率相同时，且设定相等的下垂系数，由于线路阻抗的不同，会引起电流偏差量Δi，Δui为电压偏差量。

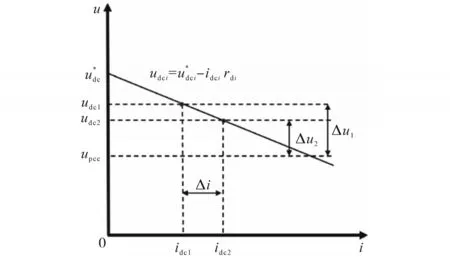
图3 传统下垂控制示意图Fig.3 The schematic of the traditional droop control

综上，由于线路阻抗不能被忽略，传统下垂控制在对电压及电流的控制精度上存在偏差，会较大地影响变换器的工作效率和直流母线的电压调节范围，甚至会影响直流微电网的稳定性，针对该问题需要提出改进方法。

2 改进下垂控制策略

2.1 改进型I—V下垂控制及建模

直流微电网中的另一种下垂控制方式，即电流—电压（I—V）控制，通常采用电流内环，原理为通过检测变换器出口侧直流母线的电压来调节电流内环的参考电流值，相比于传统V—I控制可以替代电压外环控制，参考电流值会随直流母线电压的降低而升高，再通过电流内环直接控制输出电流。I—V控制方法相对简单，省去了一个电压PI控制器，也避免了基于在电压外环控制器另增加一个下垂控制环节，从而对系统的带宽有一定限制[15]，控制框图如图4所示。I—V法的电流表达式如下：

图4 I—V控制框图Fig.4 The block diagram of I—V control

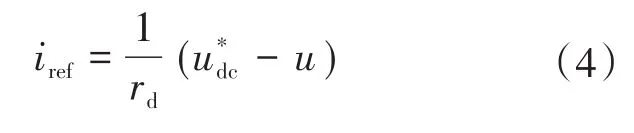
式中：iref为下垂特性输出的电流参考值。

稳态条件下，upcc为直流母线电压值，由式（4）可得：

当变换器进入动态过程后，式（5）可以改写为

式中：iref(t)为下垂特性输出电流的变化量参数；upcc(t)为直流母线电压的变化量参数。

设定mp为电压外环控制器中的比例参量，mi为其积分参量，idc(t)为变换器输出电流的变化量，则在电流内环输出的占空比可以表示为

对两边求导，再将前两式代入，可得：

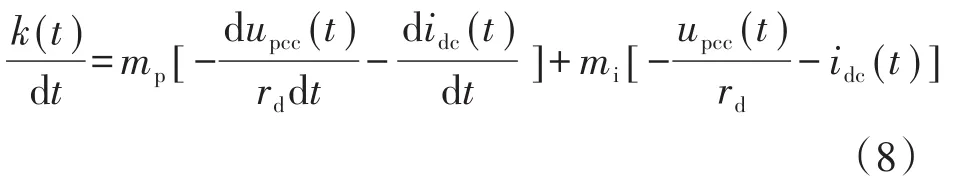
稳态条件下idc(t)的求导和动态条件下upcc(t)的求导[20]如下：

式中：uin为变换器输入侧电压值；L为变换器电感；C为直流母线电容；iload(t)为负载电流的变化量。

将式（8）～式（10）联立可求得变换器的状态空间模型如下：

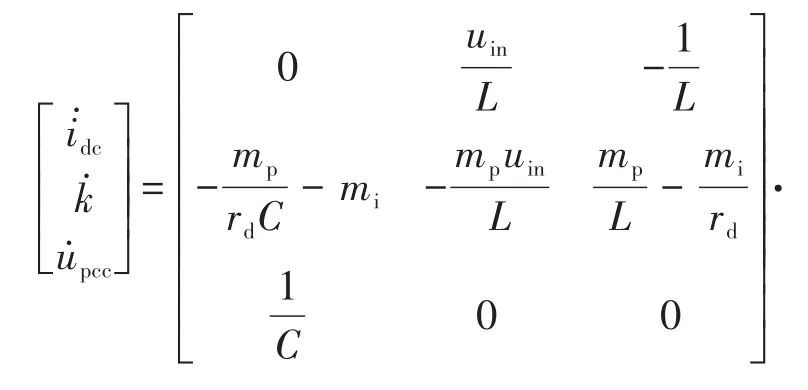
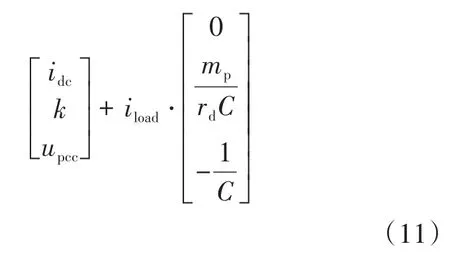
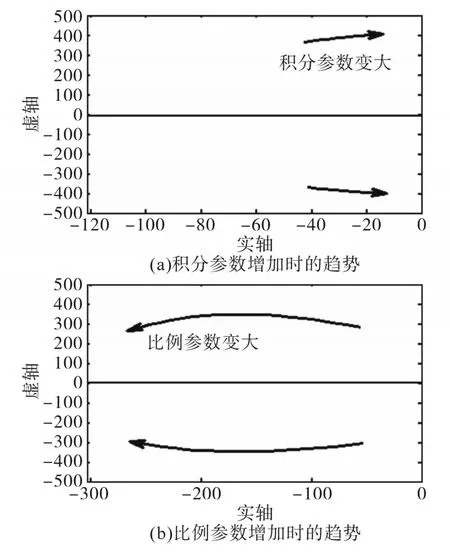
图5 参数变化的根轨迹趋势Fig.5 Root locus trend of parameter variation

设en(t)为变换器n的参考电流值与输出电流值的绝对误差，公式如下：

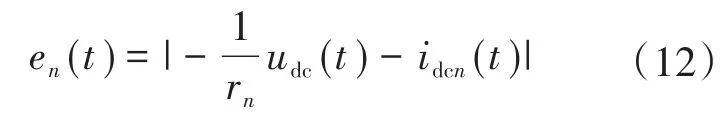
式中：rn为变换器n的虚拟阻抗。

在动态过程中，en(t)会增大，设定相对应的阈值ein，即在动态时，en(t)增大，当达到相应的阈值e2n时，应增大比例环节参数，减小输出电流的误差。

在稳态时en(t)为0。在稳态时比例参数要保持恒定，设Δimaxn为在稳态时的变换器最大输出电流值，Δumaxn为在稳态时的最大直流母线电压值，所设定的阈值需满足如下条件：

式中：Δkpn为比例参数变化量；kpn为动态前期的增量。

在对应PI控制器输出侧加入前馈补偿，目的是抑制en(t)减小到e1n时Δkpn也减小到0后控制器的占空比反向变化进而导致输出电流误差变大。定义补偿值d如下：

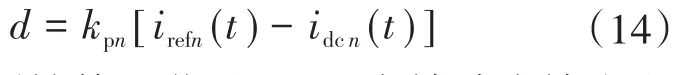
加入该项补偿环节后，可以有效减小输出电流和直流母线电压在负荷波动情况下的振荡，使两者各从动态过程平滑地过渡到稳态过程，并且提高电流的分配情况。

2.2 直流微电网母线电压无偏差控制

通过改进I—V下垂控制策略，可以提高电流的分配精度及电压的波动情况，但是依然存在输出电压有少量偏差的问题，对于直流母线电压依然有一定影响。针对该问题，本文提出母线电压无偏差控制策略，工作原理图如图6所示。

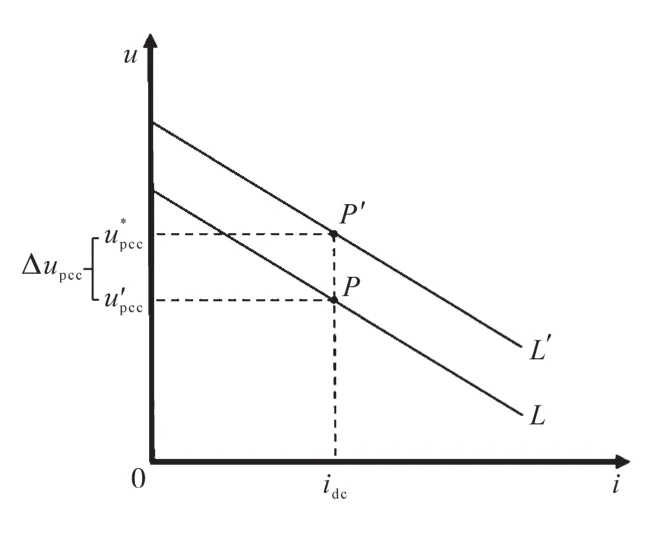
图6 母线电压无偏差工作原理图Fig.6 Working principle diagram of bus voltage without deviation

根据图2可以写出直流母线电压与输出电流之间的关系式：

为了实现直流母线电压无偏差控制，在式（15）中加入母线电压补偿项因此：

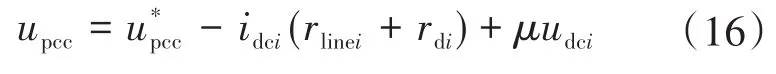
定义母线电压偏差Δudci为理想情况下直流母线电压upcc与额定值的差值，即

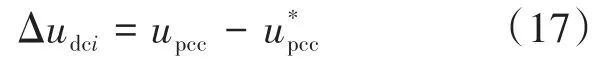
将式（16）与式（17）联立，并且等号两边同时对时间求导，同时为了保证电流的分配不受到电压平移的影响，取电流项对时间的导数为0，则有：

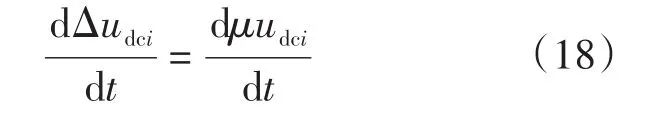
为了消除电压偏差量Δudci，电压上移补偿量μudci需要满足：

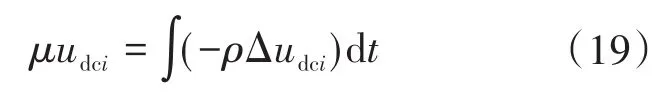
式中：ρ为收敛系数，ρ＞ 0。

将式（19）与式（18）联立，有：

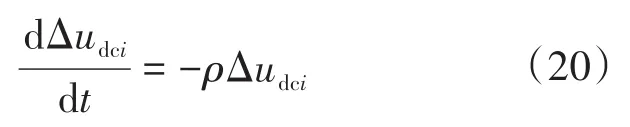
对式（20）进行求解，进一步有微分方程：

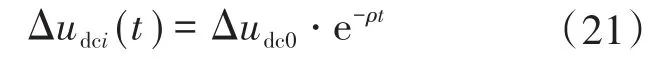
式中：Δudc0为初始时直流母线电压偏差值。

由于收敛系数ρ＞0，因此式（21）所得到的直流母线电压偏差量Δudci()t在有限时间内能收敛为0，收敛时间的快慢与收敛系数ρ相关。母线电压无偏差控制只改变母线电压值，在补偿量的设置中因电流对时间的导数为0，保证了在电压无偏差控制中电流的分配精度。因此在所提母线电压控制策略下，直流母线电压无偏差控制可以表示为

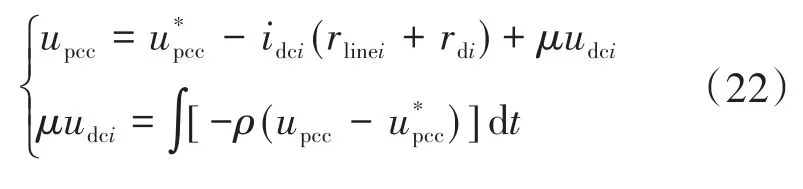
由式（22）可以看出，为了保证平移得到直流母线电压在额定值需要选择合适的收敛系数ρ，使电压偏差量Δudci在一定时间范围内收敛为0。所提电压无偏差控制策略不需要互联通信，就可以实现电压无偏差控制，并且不影响电流的分配精度，可以提高直流微电网系统的可靠性和稳定性。

2.3 带有电压补偿的改进I—V下垂控制策略

针对传统V—I下垂控制存在的局限性，本文提出一种带有电压补偿的改进I—V下垂控制策略。首先根据2.1节内容，在原有I—V控制的基础上加入改进补偿器，补偿值d用来抑制电流及电压的剧烈波动；根据2.2节加入母线电压无偏差控制，利用上移补偿原理，设置适合的收敛系数ρ，在不影响电流分配的条件下使直流母线电压保持在额定水平。具体控制系统框图如图7所示。

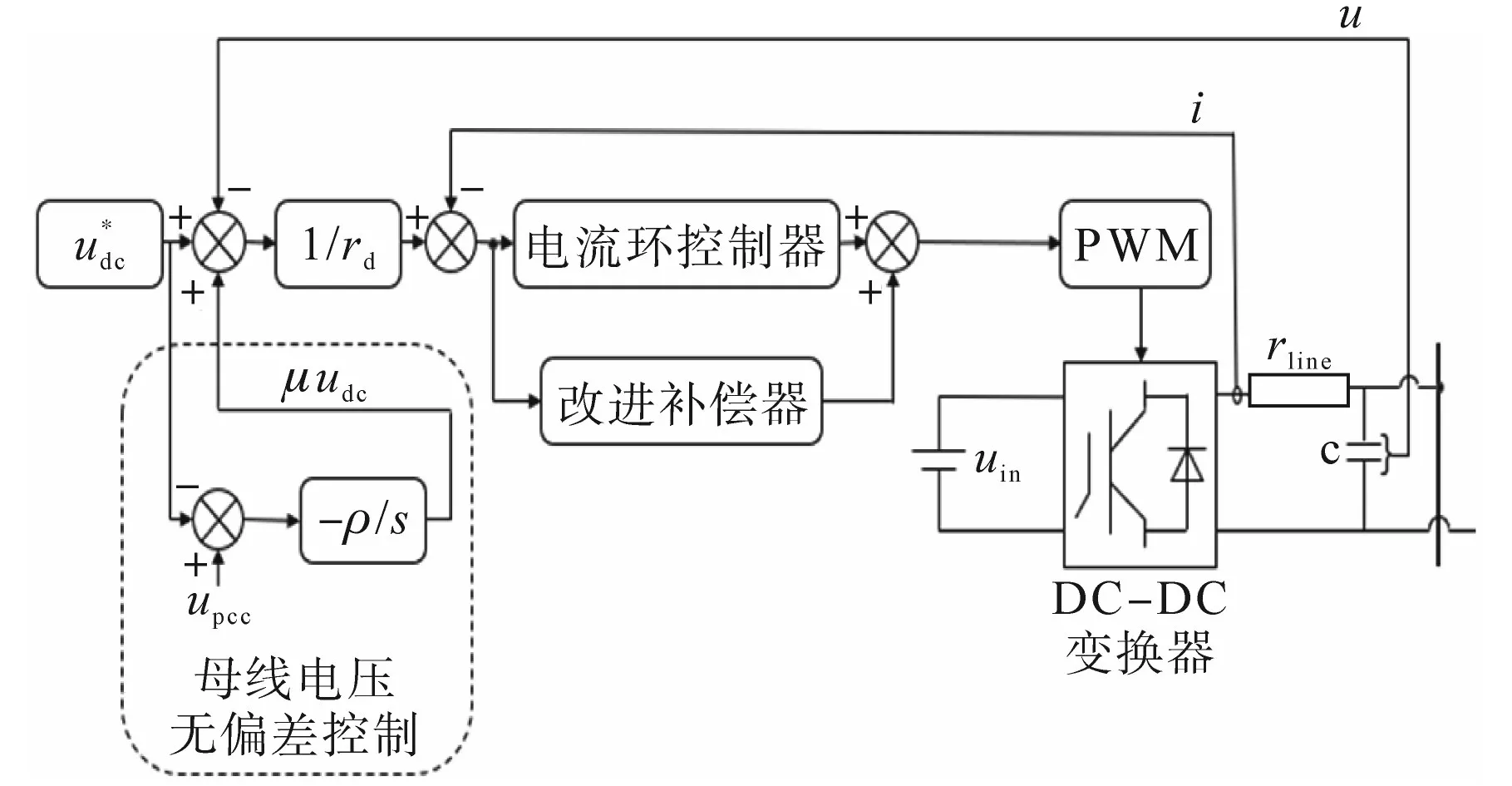
图7 改进I—V下垂控制策略框图Fig.7 The block diagram of the improved I—V control strategy

3 仿真验证

本文以2台变换器并联为例，利用Matlab/Simulink进行仿真验证，仿真参数如下：参考电压值，线路阻抗rline1=1.6 Ω，线路阻抗rline2=0.8 Ω，下垂电阻系数rd1=1 Ω，下垂电阻系数rd2=1 Ω，收敛系数ρ=10，变换器电感L=2 mH，直流母线电容C=9000 μF。比例参数设定为0.001，积分参数设定为0.01，在t=2 s时，增加1 kW公共负荷。验证负荷在波动条件下，对比传统下垂控制方法与改进型方法的控制精度。

图8a～图8c分别为传统控制、改进I—V控制以及本文所提方法的变换器输出电流仿真波形图。在图8a中因为线路阻抗rline1与rline2两者存在差异，DG的输出电流分配不均，绝对误差达到23.8%，并且在负荷变化时高频振荡较大且有一定恢复时间，会影响电源的效率。图8b中可以看出在2 s负荷波动时输出电流的振荡较图8a相比有所改善，可以有效抑制高频振荡的因素是在动态时对比例参数的调节，该参数在此状态前期较大，输出电流的恢复时间也明显小于传统下垂控制，且电流分配效果较好，误差较小。对于图8c来说，与图8a相比其输出电流在负荷波动时也能保持较小的振荡以及较短的恢复时间；与图8b相比其电流情况基本一致，说明在加入母线电压补偿后对输出电流基本无影响。

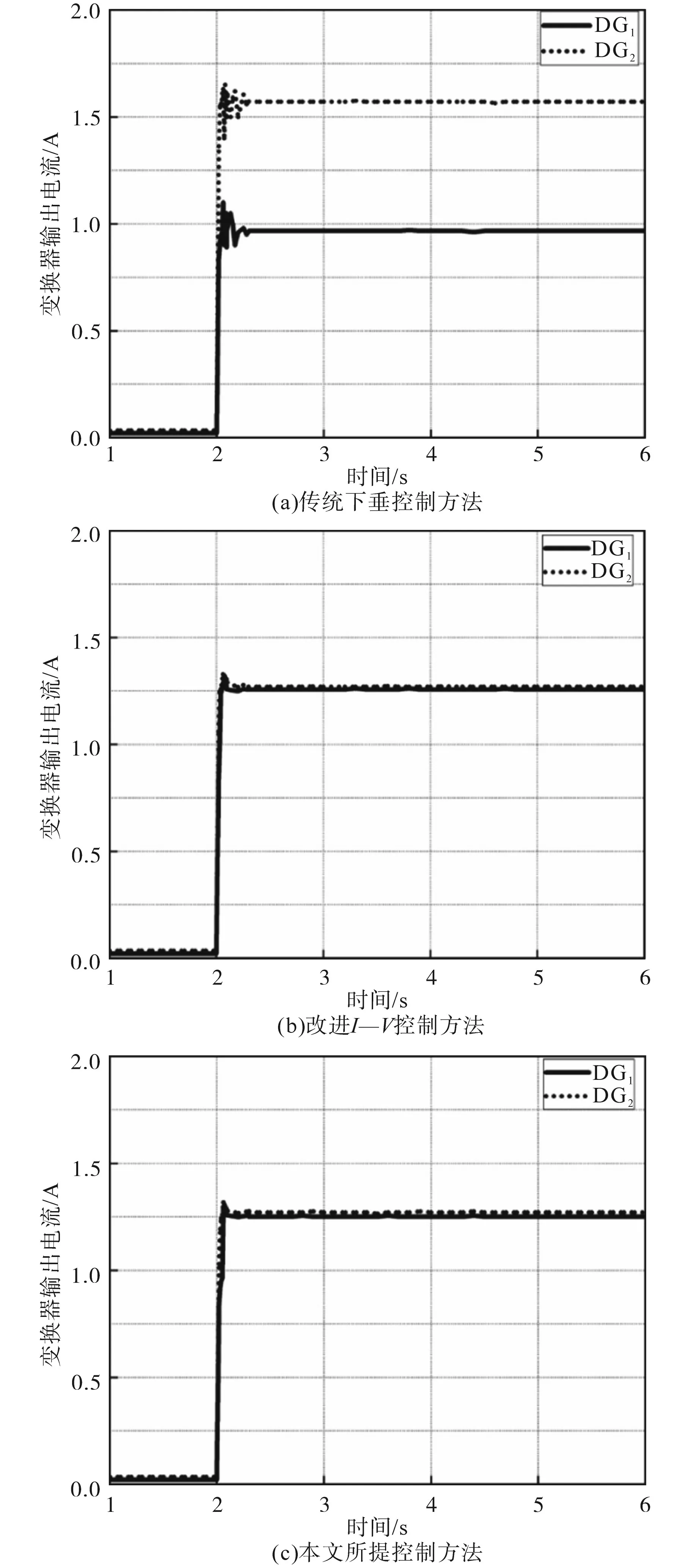
图8 变换器输出电流仿真图Fig.8 Output current simulation diagram of the converter

图9为3种控制方法下的直流母线电压仿真波形图，由于下垂控制的有差特性，母线电压无法维持在参考直流电压水平，在2 s后电压降落尤其明显，由500 V下降到488 V，会降低供电的质量。改进I—V控制方法相比于传统下垂控制方法，可以看出其振荡环节和恢复时间有明显改善，但直流母线的电压降落依然存在，无法保持在参考值。本文所提改带有电压补偿的改进I—V下垂控制策略的仿真结果可以看出，在稳态时加入了母线电压无偏差控制后，当负载在2 s发生波动时，设置相应的收敛系数ρ，母线电压upcc虽然会产生较小波动，但是在允许的时间范围（0.6 s）内可恢复至直流参考电压500 V，补偿效果较好。因此，在负荷发生波动情况下，该方法对变换器输出电流以及直流母线电压控制有良好的改善作用。该策略也符合直流微电网即插即用等特点。

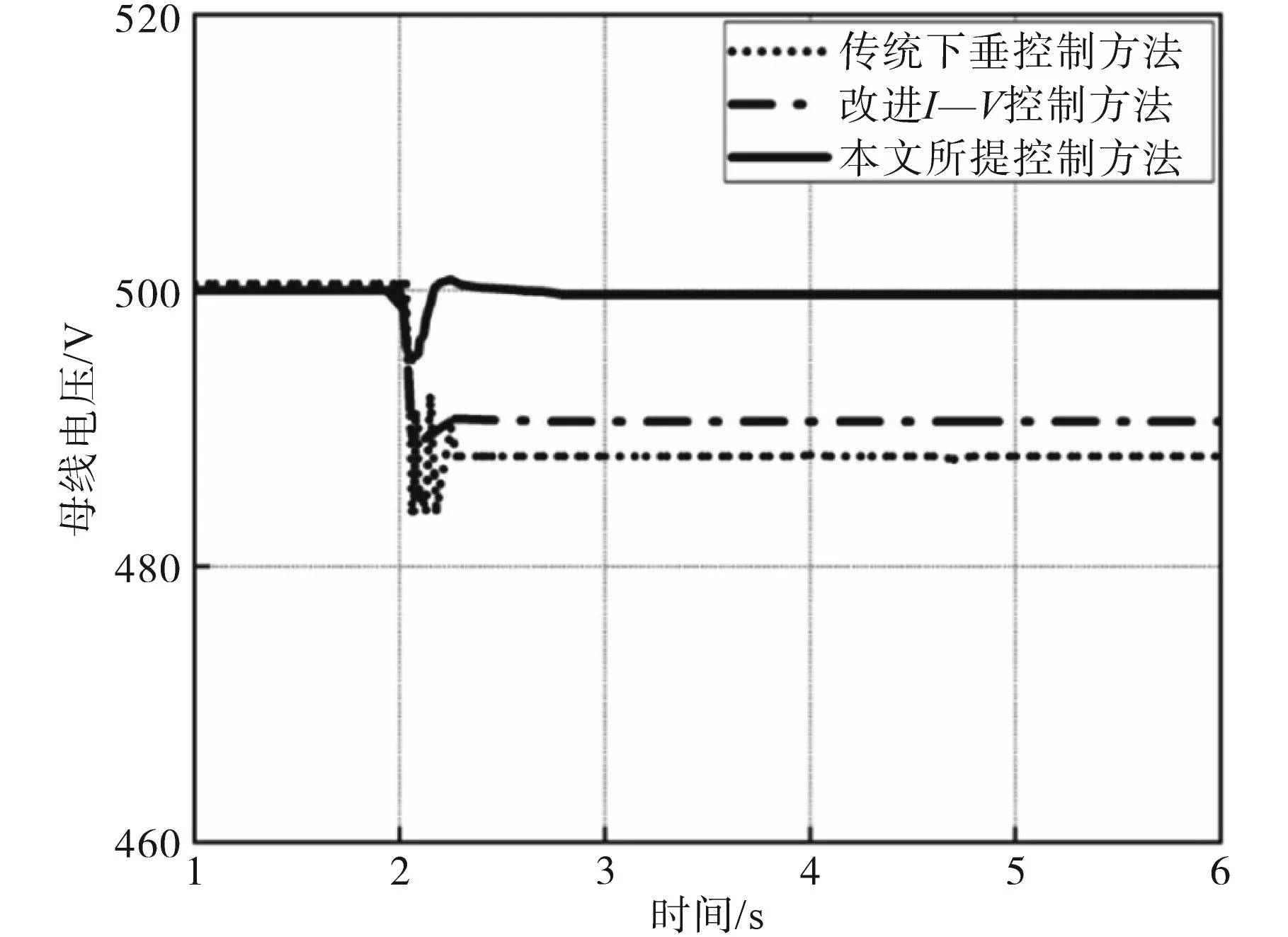
图9 直流母线电压仿真图Fig.9 Simulation diagram of DC bus voltage

4 结论

本文针对传统直流微电网V—I下垂特性中电流分配及直流母线电压控制问题提出改进策略，在I—V控制策略中加入改进补偿环节可以保证对输出电流的稳定及分配，并且在对输出电流无影响的条件下，通过平移补偿原理对母线电压进行无偏差补偿控制，设定合适的收敛系数，可以消除由下垂特性引起的直流母线电压偏差，其仿真结果验证了所提改进理论方法的有效性和优越性。