具有功率因数校正功能的谐振无桥AC/DC变换器

朱利洋，孙敏

（1.丽水学院工学院，浙江 丽水 323000；2.浙江肯得机电股份有限公司，浙江 台州 318057）

Boost变换器是继二极管桥式整流器之后传统的非隔离PFC结构。它由于拓扑结构简单而被广泛应用[1-2]。然而，它也有一些缺点，主要包括传导损耗高、控制复杂度高和开关损耗高[3]。

目前阶段常规的解决方案中，反激变换器在功率非常低的应用中占据主导地位[4-5]。为解决传统Boost变换器存在的上述问题，在以往研究中提出的技术手段主要可分成三大类：1）通过采用软开关技术来降低开关损耗[6-7]；2）通过采用诸如单级、无桥、并联PFC和交错结构等技术手段来降低传导损耗[8-10]。交错PFC作为目前较新的解决方案，在必须满足严格外形要求的硬件应用中非常受欢迎，例如在液晶电视、超薄笔记本适配器、OLED照明面板和平板屏幕中[11-13]。最近，部分研究还提出了采用超平面变换器为这些应用提供电源的解决方案[14]。该方法容易实现、使用了更多但更小的组件并且具有更好的热分布。为进一步降低导通损耗，还可以通过进一步去掉传统PFC变换器的输入整流器，由此产生无桥交错PFC变换器，以减少电流路径中的半导体元件数目；3）结合方法1）和方法2）同时提供软开关功能以及降低传导损耗功能[15]。文献[16]中对隔离谐振变换器进行了相关研究。由于变压器损耗，隔离谐振变换器的效率要比非隔离变压器低。文献[17]提出一种基于谐振SEPIC变换器的谐振无桥PFC变换器。这些变换器采用无桥结构且易于控制。然而，SEPIC结构仍存在着一些问题，如器件应力较大、软开关能力有限、结构中电容体积较大等。文献[18]提出通过使用额外开关来提供软开关的功能。文献[19]介绍一种无桥谐振Buck-PFC变换器。该变换器给半导体器件提供软开关条件，具有功率因数校正的能力。文献[20]中也提出具有PFC能力的Buck变换器的类似概念。然而，在输入电压的过零点处，当输出电压大于输入电压时，输入电流在很长的一段时间内为零。因此，在输出电压比较高的情况下，需要较大的滤波元件用来补偿较低的功率因数。

本文所提谐振无桥Boost-PFC变换器具有简单的无桥对称结构、高功率因数能力、为所有半导体提供软开关的谐振特性、低纹波的连续输入电流以及简单的调制和控制电路能力。并且其输入电流是连续的，能够在两个输入电感之间平均分配。MOSFET关断时提供零电压开关（zero voltage switching，ZVS），二极管关断时提供零电流开关（zero current switching，ZCS）。此外，所研究的PFC变换器具有功率因数校正能力。

1 谐振式无桥PFC变换器

所提无桥PFC变换器结构如图1所示。它具有将输入交流电压转换成为输出直流电压的谐振特性，而且能获得正弦连续输入电流。本节研究了所提出的变换器在不同线路周期间隔和开关周期中的行为，还给出该变换器的等效电路以及不同间隔下的电压和电流波形。图2为正半周期和负半周期所对应等效电路图。

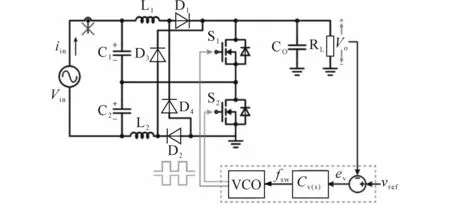
图1 谐振无桥交直流PFC升压变换器Fig.1 Resonant bridgeless AC/DC PFC Boost converter

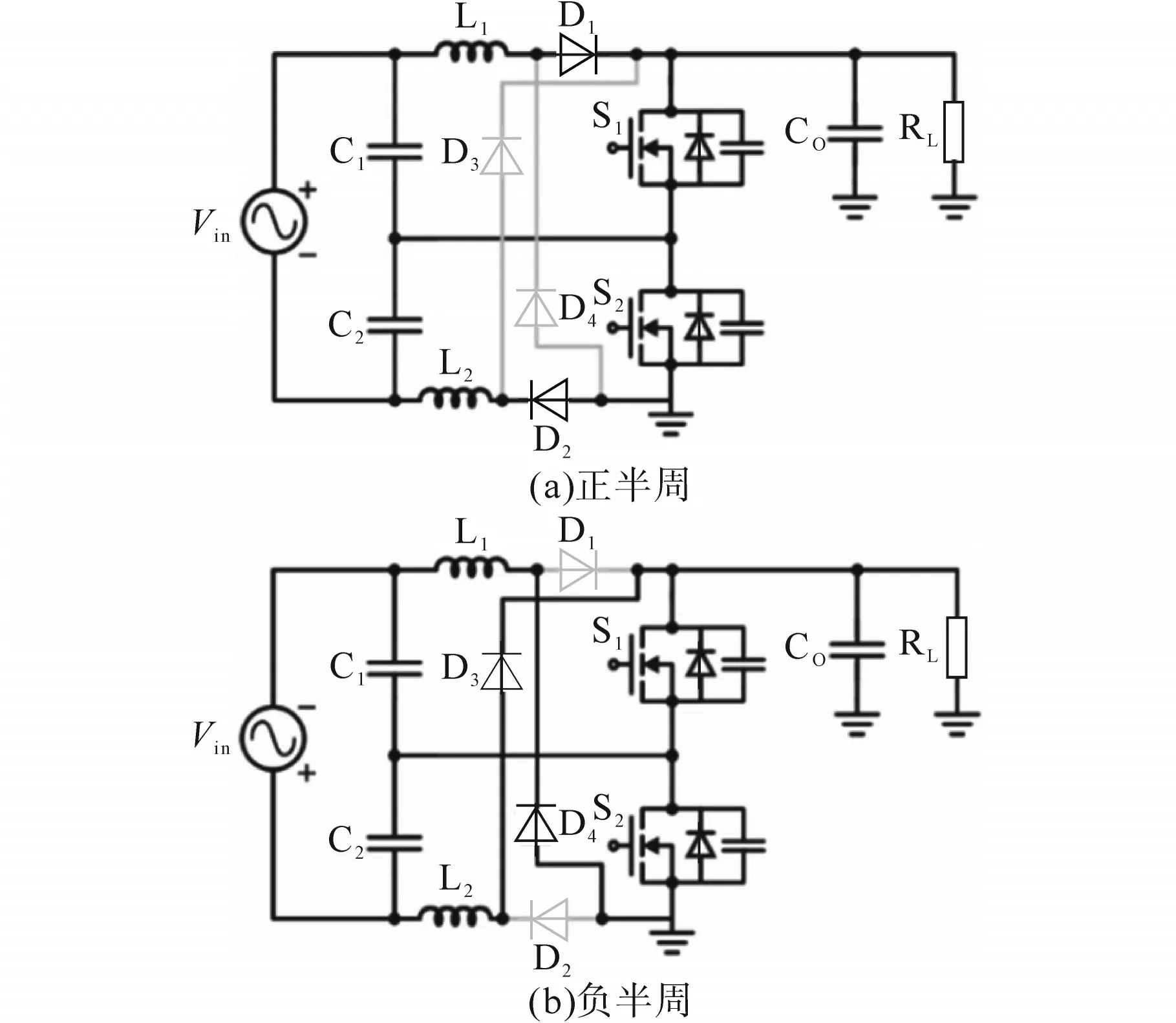
图2 所提变换器的等效电路Fig.2 The equivalent circuit of the proposed converter

为简化分析，假设除MOSFET之外，所有电路元件都是理想的，输入电容C1和C2与电感L1和L2数值相等。每个输入电容和电感可以在方程中分别用C和L表示。图2a为正半周变换器等效电路，图2b为负半周变换器等效电路。此外，图3为开关周期中的等效有源电路图。

图3 开关周期中的等效有源电路图Fig.3 Equivalent active circuit diagram in switching cycle

模式Ⅰ [t0＜t＜t1]：在开关的本体二极管开始导通时，该模式便开始运行，如图3a所示。由于S1的本体二极管导通，S1可在ZVS条件下导通。在此种模式下，S1的电流iS1为负，并呈现上升趋势。当iS1返回零（在t1时刻）时，该模式结束。此时，输入电容器的电流变成零，由于在此之前C1的电流iC1为正，因此在开关周期中，C1的电压vC1处在峰值，C2的电压vC2的电压处在最低值。

模式Ⅱ [t1＜t＜t2]：如图3b所示，流过D1和S1的电流仍是给电感L1充电。同时，L2通过D2和S1提供负载。然而，在t1以后，L1和L2的净电流iL1和iL2正从漏极流向S1源极。在这期间，iL1增加，同时iL2减少。在t2时刻，iL2接近零，这将使二极管D2在ZCS条件下关闭，从而阻止了电感向输出电容供电。在这种模式下，为简化方程，输入电容器电压（vC1和vC2）可视为下式中的常数：

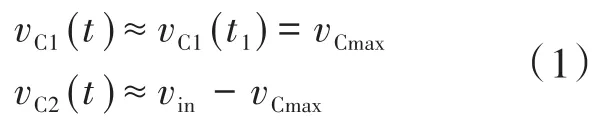
式中：vCmax为开关周期中输入电容的最大电压。如前所述，考虑到在这间隔期间通过输入电容器的电压是恒定的，那就意味着电感L1和L2的电压分别具有等于vCmax和vin-vCmax-vo的恒定电压。电感电流的相关计算公式如下所示：

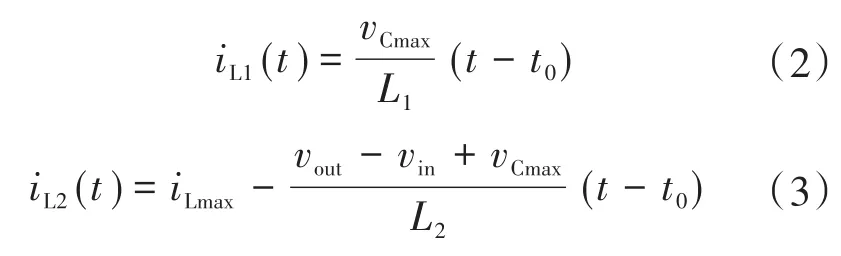
式中：vout，vin分别为开关的输出及输入电压。

模式Ⅲ [t2＜t＜t3]：如图3c所示，一旦二极管D2关闭，该间隔开始运行。在这段时间内，iL1通过S1和 D1递增，iL2为零。同时，vC1因为iC1的负值而降低。另一方面，因为iC2是阳性的，vC2正在增加。通过控制器用以关闭开关S1结束该间隔。因为在该模式下，L1与C1与C2的并联组合发生了共振，所以vC1与iL1可以用下式中的正弦方程表示：

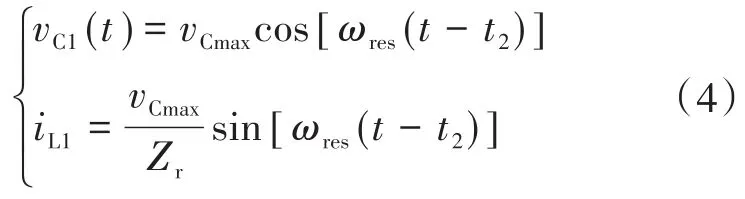
式中：ωres为谐振角频率，为输入电容器（C1和C2）与每个电感器（L1或L2）并联组合之间的谐振结果；Zr为谐振元件的阻抗。

此外，式（4）还可用于发现iLmax与vCmax之间的关系，如下式：

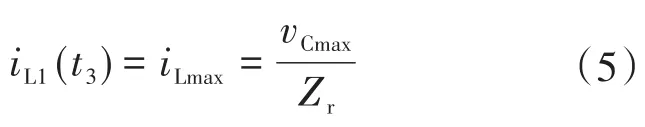
模式Ⅳ[t3＜t＜t4]：如图3d所示，启动该模式时，S1的门信号会被关闭，这导致两个开关都会被关闭。同时，L2中的电流为零，iL1在开关周期或iLmax中达到最大值。因为电感器的电流不能突然变化，所以iL1不能瞬时间达到零，而且它能够闭合其路径的唯一方法就是流过MOSFET中的漏源电容。也就是说，其有助于对S1的漏源电容进行充电和对S2的电容进行放电。如果选择开关的并联电容比较大，则在开关接通前放电该电容需要更多时间和能量，有可能在接通的时候出现ZVS条件。然而，由于放电电容的电流是每个电感器的最大电流（iLmax），即使是在轻负载条件下也可实现导通时的ZVS。在该间隔结束的时候，通过S2的漏源电容的电压会达到零，并且从该时刻起，电感电流iL1将会流过开关S2的反并联二极管。在这期间，S2可以通过放电并联电容器或者ZVS接通。

由于电路的对称性，后四种工作模式（图3e～图3h）和前四个间隔（图3a～图3d）相似，不再赘述。

2 性能分析

2.1 开关周期中逆变器的分析

假定所有变换器特性在一个开关周期内都是恒定的。首先分析输入电容上的电压。vC1和vC2的总和等于输入电压，当输入电压在线路频率周期当中变化时，此输入电压被视为恒定值：

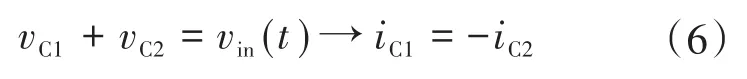
通过考虑输入电容器C1正节点和C2负节点的KCL，可得到下两式：

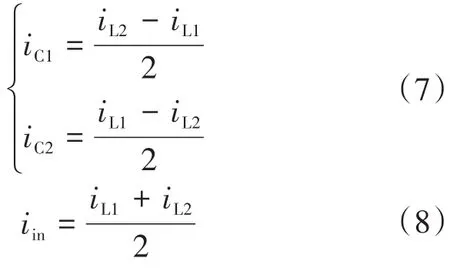
如式（8）所示，输入电流为两个电感器电流的平均值。

因为模式Ⅳ的持续时间比已经讨论的其他模式间隔短，所以可以假定电路的电流和电压保持恒定利用式（3），电感器最大电流可按下式计算：

式中：Vout为对开关输出电压的需求电压。

此外，t2时的iL1由下式得出：

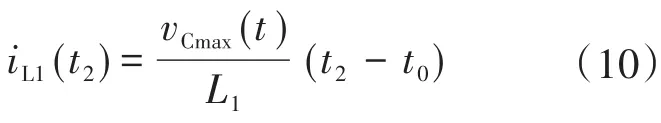
通过下式计算得到开关周期中输出电流的平均值：

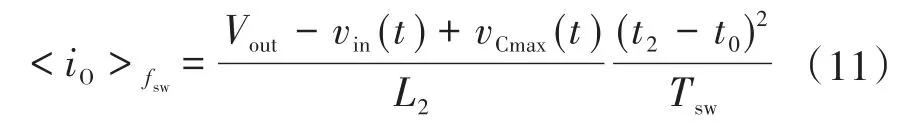
式中：fsw为MOSFET的开关频率；Tsw为开关周期。这是从t0到t2的第一和第二间隔期间完成的。

iin考虑式（8）和式（9）的连续性行为，并且其最大值iin_max在t0时刻是电感电流最大值iLmax的一半，iin_max可表示如下：

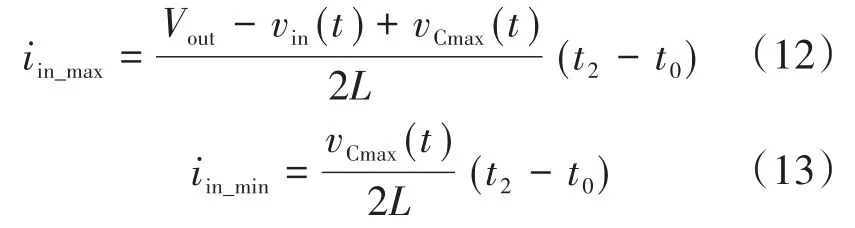
根据式（12）和式（13），可在下两式中计算出单个开关周期内输入电流的平均值和纹波：

根据式（5）、式（9），（t2-t0）可以根据Vout，vin（t）和vCmax（t）之间的关系计算，如下所示：

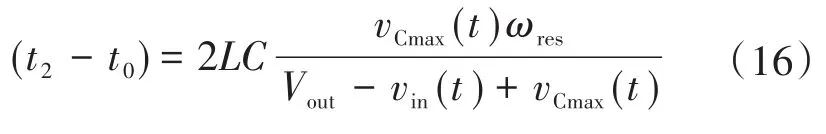
式中：ωres为谐振角频率。

消去式（11）、式（14）中的变量（t2-t0），得到如下方程：

由式（17）、式（18）可得出开关周期内的输出和输入电流平均值。需要说明的是，开关周期当中的vCmax（t）不同于峰值电压vCmaxPeak的最大绝对值。

2.2 运行周期中变换器的分析

假定输入电压为纯正弦波形，输入电流将会通过简单的恒频调制跟随输入电压。这也就意味着，只需简单的频率控制，变换器的功率因数就会很高。根据前面所描述，在线路周期内开关频率和负载恒定的情况之下，vCmax（t）/vin（t）保持恒定。使用这个特性，式（18）可以简化如下式：

式中：vinPeak为开关的输入电压峰值；VinPeak为输入交流电压峰值。

假如式（19）中出现的第二个分量在一个线频周期中的大部分时间可以忽略，就可以相对精确地假设输入电流非常的接近正弦波形。比值Vout/vCmax（t）随交流输入电压变化，电路设计应使可变vCmax（t）小于Vout。因此，如果电路设计是为了使Vout/vCmaxPeak尽可能的低，它可以导致Vout/vCmax（t）是一个小值，因此与（1-VinPeak/vCmaxPeak）相比就可以忽略不计。因此，iin（t）就可以接近正弦函数。为使分析简单化，将变量标准化。在标准化过程之中，电压、阻抗、频率和电流有相应参考值，定义如下：

式中：VinRMS为输入电压有效值。

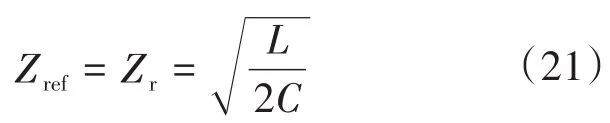
式中：Zr为谐振元件阻抗。

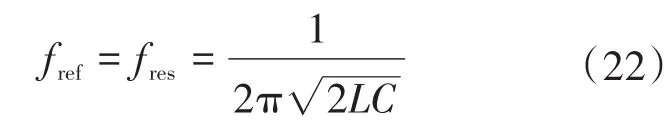
式中：fres为谐振频率。

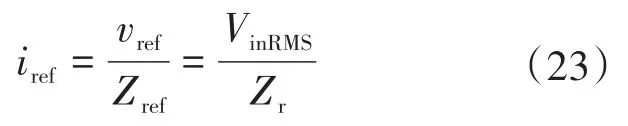
使用式（20）～式（23）中的定义，所提电路中变量可以转化为如下：

式中：Fn为归一化开关频率；Q为输出导纳或品质因数的标准化值；Rout为输出电阻；mv为变换器增益，即输出电压与输入电压RMS值的比值；vCmaxn为输入电容器最大电压的标准化值。

使用式（24）～式（27）中的定义后，后文方程式将变得更加简单。

利用式（24）～式（27），式（17）、式（18）中的定义可得到下式：

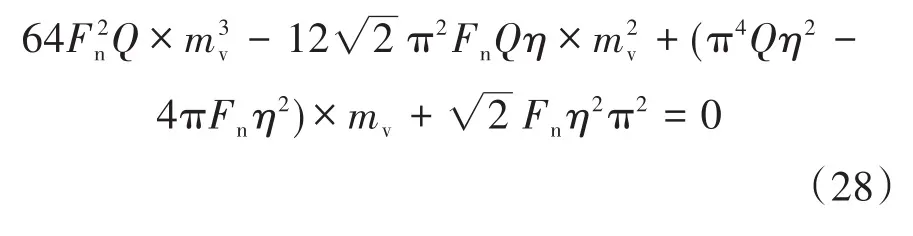
式中：η为变换器效率。

式（28）可以采用不同的Fn和Q值进行数值求解。

根据式（24）～式（27）中的定义，以及式（17）和式（18），可以得到不同Fn时表示vCmaxn值的计算公式如下：

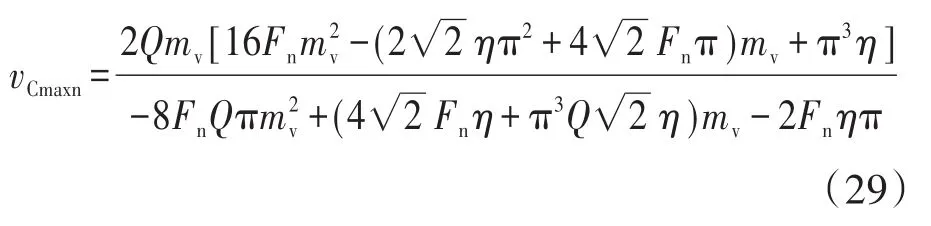
为使分析和设计更具有可读性，将式（20）～式（23）中定义的变量进行规范化。iref为电压基准（vref=VinRMS）与阻抗基准（Zref=Zr）之比。因而，基于式（5），电感的最大电流归一化值将等于电容器的最大电压：

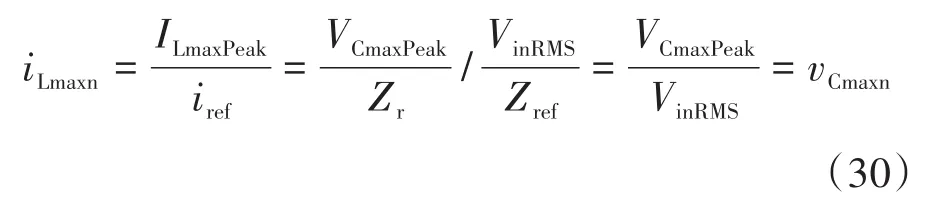
依据式（30），iLmaxn的最大值等于vCmaxn的最大值。利用式（29）计算vCmaxn或iLmaxn。电感电流的平均值可通过取式（8）的平均值来计算。因为电感L1和L2电流的平均值相等，所以它们的平均值可以用iLaveg表示，其计算如下：

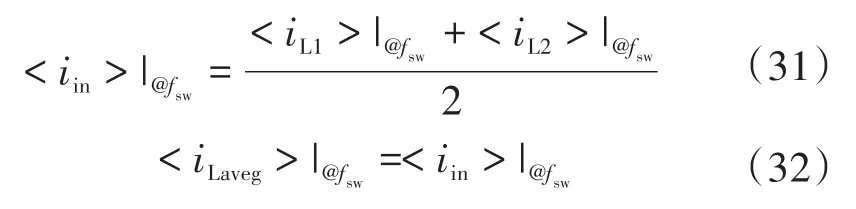
式中：＠fsw为相应参数对应的开关频率。

因此，开关频率中的电感电流平均值等于输入电流，输入电流可以认为是正弦的。此外，半导体电压与输出电压相等。

3 算例分析

在额定输出功率为400 W的实验装置进行测试。实验设计原型如图4所示。

图4 基于所提结构的原型设计图Fig.4 The picture of the designed prototype based on the proposed structure

为分析所提变换器性能，将设计的变换器跟具有相同元件及输入输出规格的交错Boost变换器进行性能比较。如果传统交错Boost变换器当中的电感具有不连续电流，那么输入电流本质上可以近似正弦，而无需任何的电流回路。如果输入电压峰值和输出电压之间差值越大，电流就越近似正弦。因此，这种传统的电路具有许多与所提变换器相近的特性，包括与所提出的结构相比仅具有两个以上二极管的相似数量的元件，以及具有DCM电感电流固有的PFC能力。但是，交错并联DCM升压的唯一问题是输入电流的纹波比所提出变换器中的连续输入电流的纹波更高，在轻、中载时完全不连续。这就迫使设计人员在传统变换器中需要使用大的无源元件作为滤波器。因此，所提变换器的整体体积要比传统的DCM交错升压小。此外，所提变换器可为二极管提供零电流开关，为开关管提供零电压开关，而传统的DCM-Boost变换器就不行。换言之，传统DCM-Boost变换器在打开开关前不能对二极管和开关的寄生电容放电。这导致了MOSFET的并联电容器在导通时会放电到开关中，限制了传统Boost变换器在高频段的性能。

图5为所提变换器与交错Boost变换器的效率对比图。

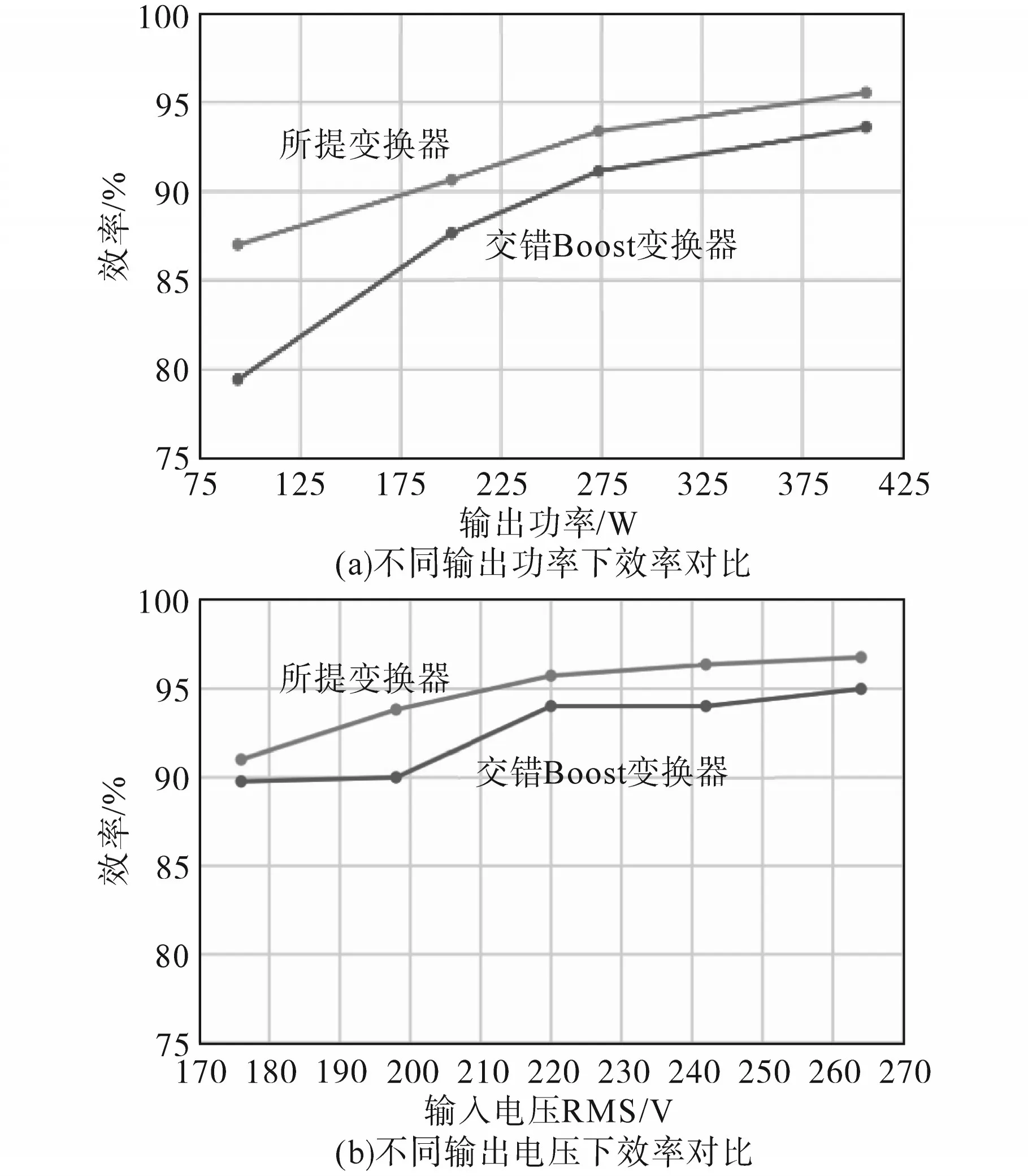
图5 效率对比Fig.5 Efficiency comparison

交错Boost具备与所提变换器标称频率（230 kHz）相等的恒定开关频率的相同组件。这将有助于保持交错Boost的高效率。尽管在较轻负载中，交错Boost变换器开关频率与所提变换器相比相当的低，但效率并不高，如图5a所示。图5a展示出与具有相同组件的传统交错Boost变换器相比较。在额定输入电压作用下，从轻负载到满负载的条件下，所提变换器效率始终高于交错Boost变换器效率，其中，轻负载时所提变换器效率提高约8%，在满负载下效率提高约2%。在图5b中，将所提变换器在不同输入电压下的效率跟传统DCM Boost变换器的效率作了比较，所提变换器效率依然是始终高于交错Boost变换器效率。

此外，传统的交错Boost变换器跟70 μH电感和230 kHz开关频率一起工作时，它的每个电感电流在整个工作条件下总是不连续的。即使满载时也会发生这种情况。所以说，即使没有电流环，电流不连续的低电感交错并联Boost变换器也是可以具有高功率因数的。交错Boost变换器的输入电流为两个电感电流之和。在规定工作条件下，传统变换器输入电流仅在很小一部分线路周期内为连续的。然而，由于结构当中不使用滤波元件，即使在额定负载条件下，输入电流在大多数线路周期内也为不连续。这将会降低功率因数并显著的增加THD。

图6为所提变换器与传统交错Boost变换器在满负载时输入电压、电流和输出电压对比。

图6 满负载输入电压、电流和输出电压对比Fig.6 Comparison of input voltage，current and output voltage at full load

图6a为满负载时，所提出的变换器的输入电流、输入电压及输出电压波形图。图6b为满负载时，交错Boost变换器的输入电流、输入电压及输出电压波形图。两个变换器均为满负荷运行，为更好地观察变换器的工作情况，这些波形的测量无需采用任何滤波器元件。这就意味着所提的变换器的输入特性就类似于CCM变换器，即使是使用小电感，该变换器的功率因数测量值也是接近于1。同时这也表明了，在实现相同功能的情况下，所提出的变换器所需输入滤波器的尺寸将会小于传统的交错Boost变换器。

图7为所提变换器与交错Boost变换器的功率因数和总谐波失真（THD）对比图。可见，所提出变换器的功率因数是大于在不同负载水平下具有相同组件的传统变换器功率因数的。由图6可知，交错Boost的输入电流在大部分的线路周期中是不连续的。然而，在相同工作条件下，输入电流在相同电感下是连续的。伴随着输出功率的减小，交错Boost的输入电流变得更加不连续，导致PF减小或是THD的增大。该特性在图7a、图7b中是以不同的输出功率电平来体现的。探究上述现象的原因，主要是所提出变换器的软开关技术是在硬开关电路的基础上，增加了小电容、电感等谐振器件，构成了辅助换流网络，在开关过程的前后引入了谐振过程，开关在其两端电压为零时导通；或是使流过开关的电流为零时关断，使得开关条件得以改善，降低传统硬开关的开关噪声和开关损耗，从而提高电路的效率。最终通过实现开关管的零电压开关和零电流开关，来降低开关管的开关损耗，进而提高变换器的功率密度和效率。

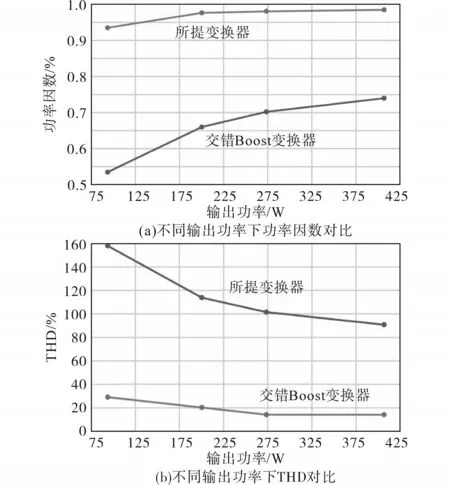
图7 功率因数以及总谐波失真对比Fig.7 Comparison of power factor and total harmonic distortion

4 结论

本文提出了一种具有高功率因数特性和高频的谐振无桥PFC变换器，并完成了理论分析和实验研究。所提出的变换器能以较低的THD提供连续的输入电流，甚至能够以不连续电流提供较小的电感。此外，算例分析也表明所提出的变换器能够为结构中的所有半导体提供软开关功能，这将有助于提高整体效率。进一步研究表明，与具有相同元件的传统交错Boost变换器相比较，该变换器在满负载情况下的效率提高了2%，在轻负载情况下的效率提高了8%以上，可见所提的变换器所具备的优越性及其在工程中的实用性。