折叠网壳结构在不同参数影响下表面风压分布系数规律研究

黄政 颜卫亨

1.中国市政工程华北设计研究总院有限公司 天津300074

2.长安大学建筑工程学院 西安710061

引言

折叠结构具有展开折叠方便快捷、机动性强等特点，是一种新型结构体系，在民用及军事领域得到广泛应用。此类结构对风雪荷载效应较为敏感，故风荷载计算往往是设计的控制工况之一。对于此类折叠网壳结构表面平均风压系数分布已有研究做了不少工作［1-4］，但对于其在不同参数影响下缺乏系统而全面的平均风压系数分布规律研究。基于此，本文在不同风速、风向角、结构单元长度、端门倾角影响下，研究其在各种不同工况条件下表面平均风压系数的分布规律，为此类结构形态优化和研发新型折叠体系提供理论依据。

1CFD计算模型和参数

本文以长度为18.93m、宽度为10.6m、高度为5.63m 的折叠网壳结构［1］为研究对象（图1）。文献［2］完成了该结构在A 类地貌粗糙度类别下不同风向角、不同风速下的风洞测压试验，如图2 所示。

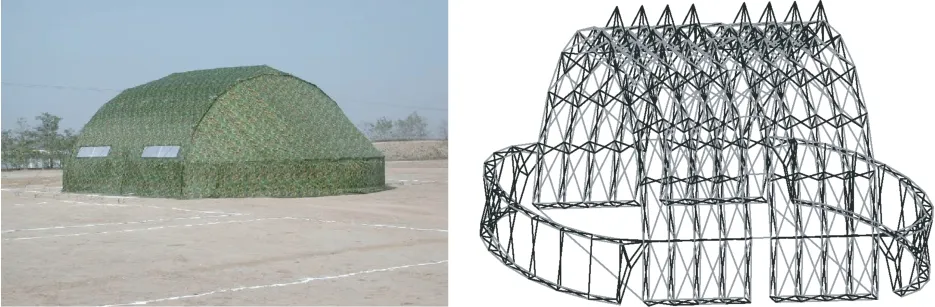
图1 折叠网壳结构外观与骨架Fig.1 External appearance and skeleton figure of folding shell structure

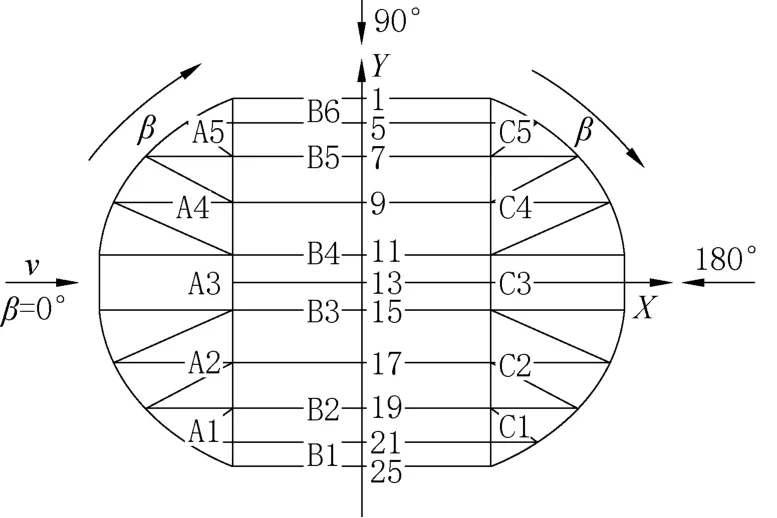
图2 风向角和结构分区的规定Fig.2 Provisions of wind direction and structure zoning

近地面风场的控制方程为Navier-Stokes 方程。理论上直接数值模拟的方法可以精确地描述流体中所有尺度的湍流和流场特性的变化，工程上常采用对Navier-Stokes方程平均的方法来计算流体的湍流流动：

2 不同参数对风压分布影响分析

2.1 风场影响分析

1.不同风速影响分析

从图3 可以看出，在相同风向角不同风速下，尽管三种风速变化范围较大，但由CFD 数值计算所得各分区平均风压系数总体上均非常接近。如在0°风向角下，三种不同风速下平均风压系数相差最大的区域发生在B1 区，分别为-0.64、-0.69 和- 0.76，极值偏差为18%，而其他各区的平均风压系数偏差均在9%以内；由此可知，风速对平均风压系数分布规律的影响并没有使折叠网壳结构表面风压分布出现差异性，其影响可以忽略不计。

图3 风速对平均风压系数的影响Fig.3 Influence of wind speed to average wind pressure coefficient

2.不同风向角影响分析

在A类地貌风速为20m／s条件下，风向角分别为0°、15°、30°、45°、60°、75°、90°下对其表面分区平均风压系数进行CFD 数值计算分析，计算结果如图4 所示。

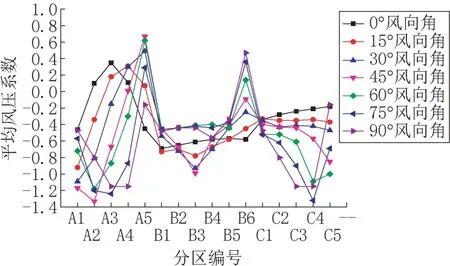
图4 风向角对平均风压系数的影响Fig.4 Influence of wind direction to average wind pressure coefficient

由图4 可见，随着结构所处风场中风向角的变化，其表面各分区平均风压系数取值起伏较大，并出现正负值不一样的震荡情况。如A5 区，在0°风向角，其取值为-0.64，而45°风向角，其取值变为0.71，当90°风向角，其取值再次减小为0.12；始终处于背风面或侧风面的A1、B1、B2、B3、B4、C1、C2、C3、C4 区均承受风的吸力作用；通过以上分析可知，风向角对平均风压系数分布规律起着控制作用，而其关键控制风向角工况为0°、45°、90°。

2.2 结构体型变化影响分析

在满足折叠网壳结构使用功能要求的同时，改变折叠网壳的主体拱结构长度L和端门截面倾角α，结构尺寸如图5 所示。对其在0°、45°、90°风向角下平均风压系数的分布规律进行探讨。

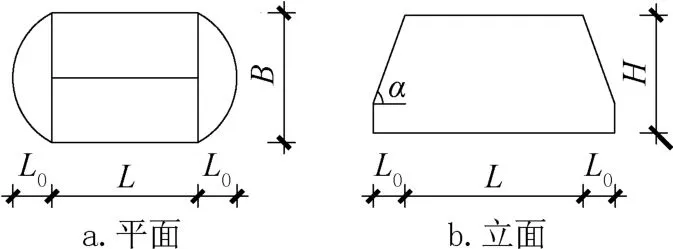
图5 结构形状尺寸Fig.5 The structure shape and size

1.结构单元长度变化影响分析

折叠网壳结构初始形态尺寸为L＝11.424m、B＝10.6m、H＝5.63m、L0＝3.753m、α ＝56°，保证结构宽度B、高度H、端门长L0和端门截面倾角α不变，改变拱结构长度L，分别对主体拱结构增加2、4、6、8 个拱肋子（单个拱肋子的长度为1.428m）共4 种工况下平均风压系数分布规律进行研究。

由图6 可知，在0°风向角工况条件下，主体拱结构长度L（拱肋子由2 个增加到8 个）变化，A区平均风压系数的取值基本没有出现差异性。B区平均风压系数随着结构拱肋子的增加逐渐减小，但当主体结构拱肋子由6 个增至8 个时，B区平均风压系数的取值不再减小，说明随着主体结构拱肋子的增加并不能一直减小B区平均风压系数的取值。除C1 和C5 区外，随着主体结构拱肋子的增加，C区平均风压系数的取值基本没有出现差异性。在45°风向角工况条件下，结构表面各分区平均风压系数的取值并没有呈现出0°风向角条件下较为规律性的变化，随着主体结构拱肋子的增加，A4、A5、B1、B5、B6 各分区的平均风压系数基本保持不变，其余各分区的平均风压系数的取值均出现不同程度的起伏，如在A1、A2、A3、B3、B4、C4、C5 等区域平均风压系数出现极值，说明主体结构拱肋子的增加将导致平均风压系数的取值明显增大。在90°风向角工况条件下，随着主体结构拱肋子的增加，结构表面各分区平均风压系数的取值均出现不同程度的增加，尤其在A3、A4、B1 ～B4、C1 ～C5 等区域平均风压系数显著增加，如A4 区由-1.03 增至-1.06，再增至-1.19，最后增至-1.20。通过以上分析可知，主体结构拱肋子增加对结构平均风压系数分布规律起着控制作用，并且随着主体结构拱肋子的增加将导致结构表面部分区域的平均风压系数取值显著增大。

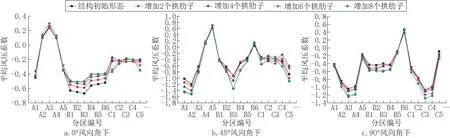
图6 结构单元长度对平均风压系数的影响Fig.6 Influence of structure length to average wind pressure coefficient

2.端门倾角变化影响分析

在满足折叠网壳结构使用功能和排水要求的条件下，同时考虑减弱端门处兜雪效应等要求，保证主体拱结构长度L和宽度B不变，通过改变结构的端门截面倾角α的变化，分别对端门截面倾角α为30°、35°、40°、45°、50°、55°、60°、65°、70°共9 种工况下平均风压系数分布规律进行研究。

由图7 可知，在风向角为0°工况条件下，折叠网壳结构端门倾角由30°增加到60°时，A1 和A5 区平均风压系数的取值基本没有变化，承受风的吸力作用，但在端门倾角为65°和70°时，A1 和A5 区平均风压系数的取值由负值变为正值，承受风的压力作用，如A1 区由-0.35 变化至0.35。而B区平均风压系数的取值均为负值。当端门倾角增加到65°和70°时，C区平均风压系数的取值表现出一定的起伏性。在风向角为45°和90°工况条件下，随着端门倾角的增加，平均风压系数的取值呈现出相同的变化趋势，没有出现明显的波动。仅在风向角为45°时，A5 和B6区平均风压系数的取值出现正负值不一样震荡情况。对于折叠网壳结构承受风吸力作用的区域，平均风压系数取值的变化规律随着端门倾角的增加逐渐减小。对于折叠网壳结构承受风压力作用的区域，平均风压系数取值的变化规律随着端门倾角的增加逐渐增大。但在风向角为90°时，其变化规律则相反。

图7 端门倾角对平均风压系数的影响Fig.7 Influence of side door angle to average wind pressure coefficient

图8 进一步给出了在风向角为0°时，端门倾角为30° ～70°结构表面平均风压系数分布云图，同样可以得出，对于折叠网壳结构A 区域，随着端门倾角的增加，平均风压系数取值绝对值呈现出逐渐增加的趋势，并且取值出现正负值不一样震荡情况。对于B 区域，当端门倾角为30°时，平均风压系数的取值最小。而对于C 区域，平均风压系数取值出现显著的起伏性。通过以上分析可知，端门倾角对折叠网壳结构平均风压系数分布规律起着控制作用，且在不同风向角工况条件下，通过改变端门倾角将导致平均风压系数的取值分布规律出现显著起伏的情况。

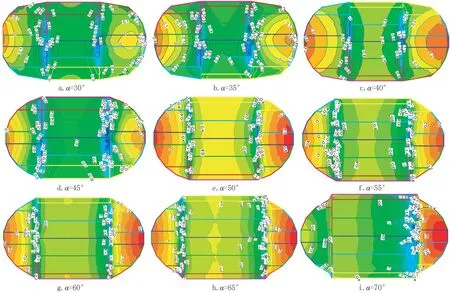
图8 0°风向角下不同端门倾角表面平均风压系数分布Fig.8 Distribution of the surface average wind pressure coefficient with different side door angle under 0° wind direction

3 结论

本文结合已有折叠网壳结构的研究成果，对其在风速、风向角、结构单元长度、端门倾角不同参数影响下，表面分区平均风压系数分布规律进行了系统研究，相对于折叠网壳结构初始形态，这对研发新型折叠网壳结构具有非常重要的理论和应用价值。相关研究工作得出以下结论：

1.除风速外，风向角、结构单元长度、端门倾角均是影响折叠网壳结构表面平均风压系数分布规律的关键参数。

2.主体结构拱肋子的增加，折叠网壳结构各分区平均风压系数的取值将明显增加，使用时可以根据要求，适当扩展结构单元长度，但要做好抗风措施。

3.折叠网壳结构端门倾角是影响结构形状优化的关键因素，为满足结构的排水和使用功能的要求，优化结构的端门倾角可以使其表面风压分布趋于均匀，有效地降低结构的风致响应。