旋转抛物面和球面构成广义牛顿环的干涉图样

金伶艳，胡 玲，顾菊观，穆成富

(湖州师范学院 理学院，浙江 湖州 313000)

普通的牛顿环是在底部放一个水平的平板玻璃，在平板玻璃上倒扣曲率半径很大的一个平凸透镜，它们中间会形成空气劈尖。空气薄膜在不同位置它的厚度不同，在空气薄膜的上表面的反射光和经过下表面的反射光会发生干涉，形成明暗相间的等厚干涉条纹。近年来结合牛顿环实验的模拟仿真研究也越来越多[1-4]。

原则上任意两种透镜组合都可以形成空气劈尖，从而可以看到等厚干涉图样[5]。文章讨论由二次函数旋转形成的旋转抛物面与单个平凸透镜(或平凹透镜)组合而形成的牛顿环装置，研究这样的广义牛顿环装置在光束垂直照射时会出现的干涉图样。

1 普通牛顿环干涉原理及图样

普通牛顿环在一般教科书中都有讲述[6]。为了后面对比方便，先简单描述一下。

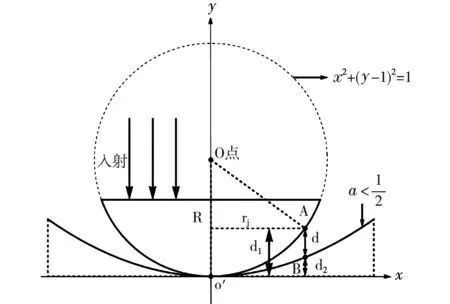
如图1所示，平面玻璃板A上放一个曲率半径为R的平凸透镜BO′C，平板玻璃与透镜之间存在厚度不同的空气薄膜，在接触面上，以OO″轴上一点为圆心，r为半径的圆周上，各个点的空气薄膜厚度均为d，由几何关系知r2=r2-(R-d)2，由于R≫d，略去高阶小量，有：

(1)

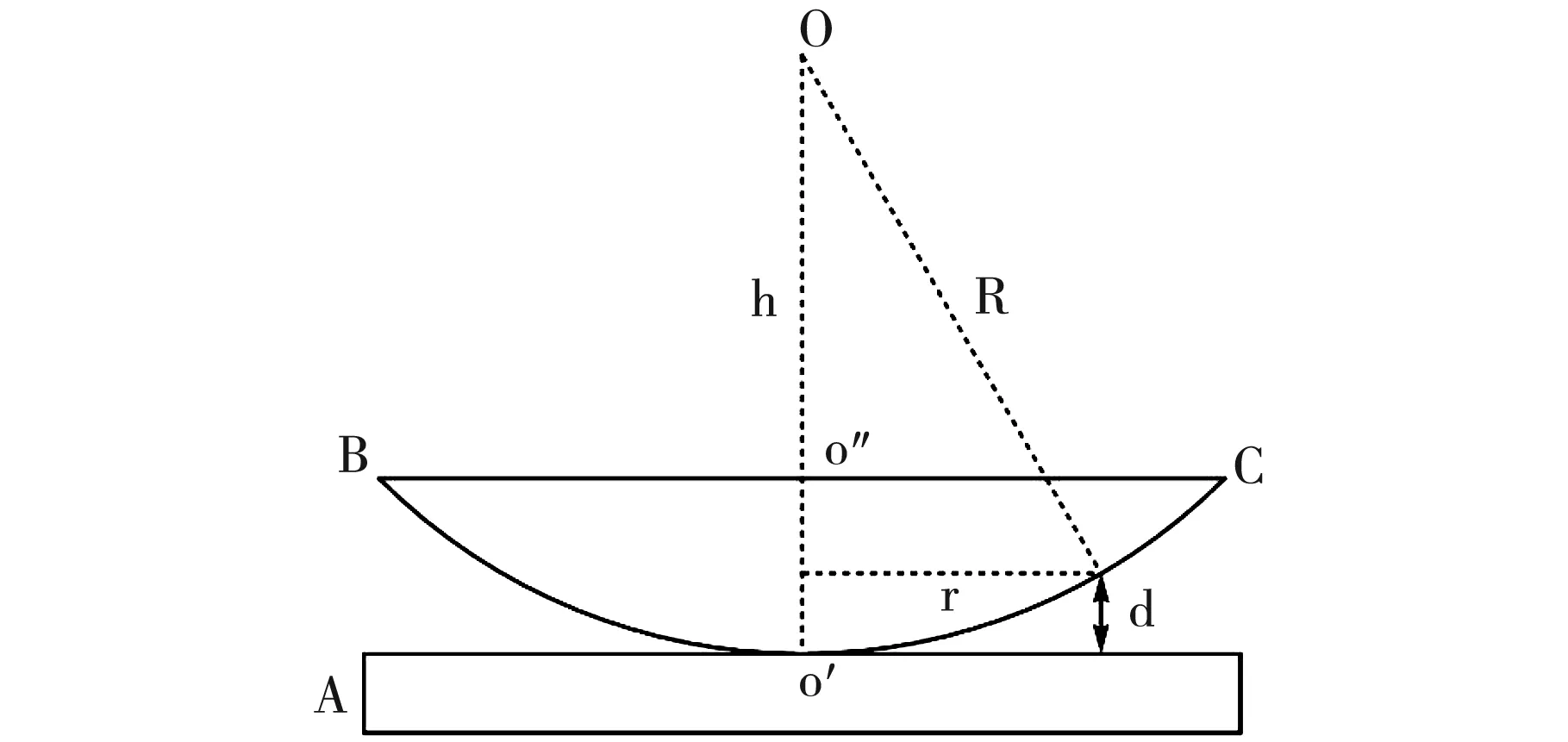
图1 普通牛顿环

考虑半波损失的影响，则两束反射光的光程差可以表示成[6]：

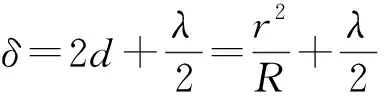
(2)

第j级明环和暗环的半径分别为：

(3)

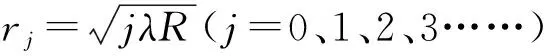
(4)

牛顿环的光强分布为：

(5)

用波长λ=589 nm的钠黄光，取透镜的曲率半径r=1 m，用Mathematica数值模拟可画出普通牛顿环的干涉图样及其光强分布图，分别如图2(a)与图2(b)所示。

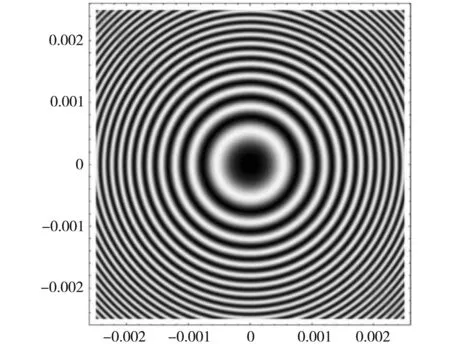
(a) 普通牛顿环干涉图样

2 旋转抛物面与平凸透镜(平凹透镜)构成组合透镜的干涉公式推导

图3为由旋转抛物面与平凸透镜组合构成的广义牛顿环截面示意图(平凹透镜情况类似)。由(1)式结果可知

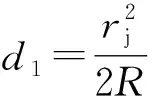
(6)

讨论最简单的二次函数，设抛物线方程为：

y=ax2

(7)

圆的方程为：

(y-R)2-x2=R2

(8)

同一级牛顿环在下表面(即抛物面)上点B的厚度为d2，则B点坐标为(rj,d2)，B点满足抛物线方程，有

d2=arj2

(9)

联立(6)和(9)式可以求得上下表面的厚度差

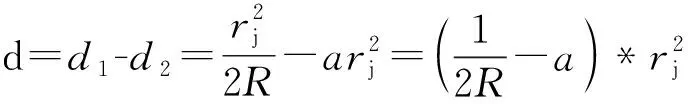
(10)

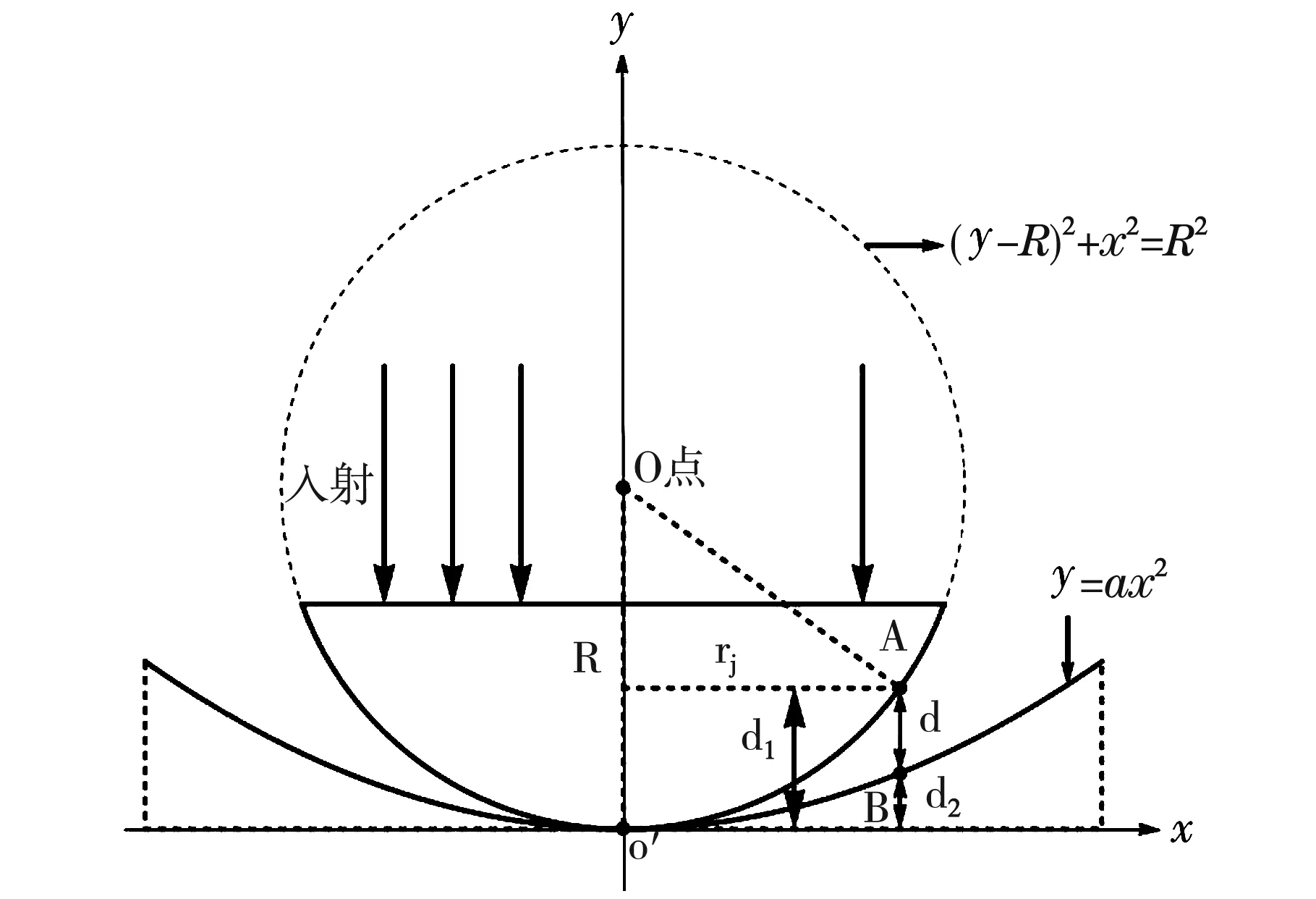
图3 旋转抛物面与平凸透镜构成组合透镜装置截面图

考虑半波损失后对应的光程差为

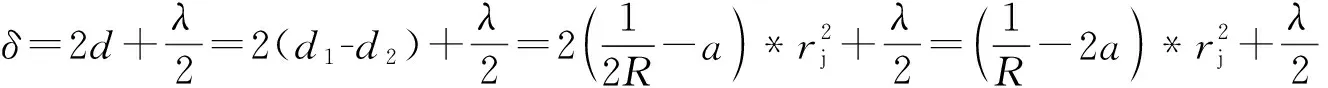
(11)

对应的光强分布为

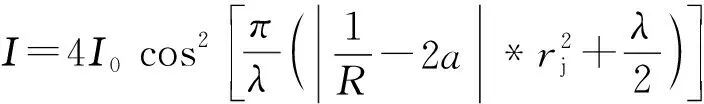
(12)

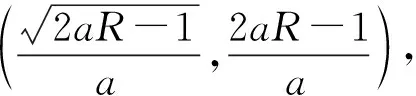
时的情况

3 利用Mathematica模拟组合透镜下的牛顿环干涉

3.1 当R固定改变二次函数斜率a的牛顿环干涉图样和干涉光强分布曲线

据在(12)式所推导的组合透镜下的牛顿环干涉图样的公式，可利用Mathematica模拟图3所示组合牛顿环装置的干涉图样。当用钠黄光波长λ=589 nm，当固定半径r=1 m时，改变二次函数的斜率a，可以得到不同的干涉图样和干涉光强分布曲线。取r=1 m，a=0.3,0.8,1,利用Mathematica模拟可得任意半径下的牛顿环干涉图样以及光强的分布曲线，如图5、图6、图7所示。由图5可知，在(-0.002 5,0.002 5)区间内亮环的最高干涉级为4级，暗环的最高干涉级为5级，随着距离中心点的距离的增加，相邻条纹间距变窄，牛顿环干涉条纹逐渐变密集，呈现出中间疏，边缘密的形状。

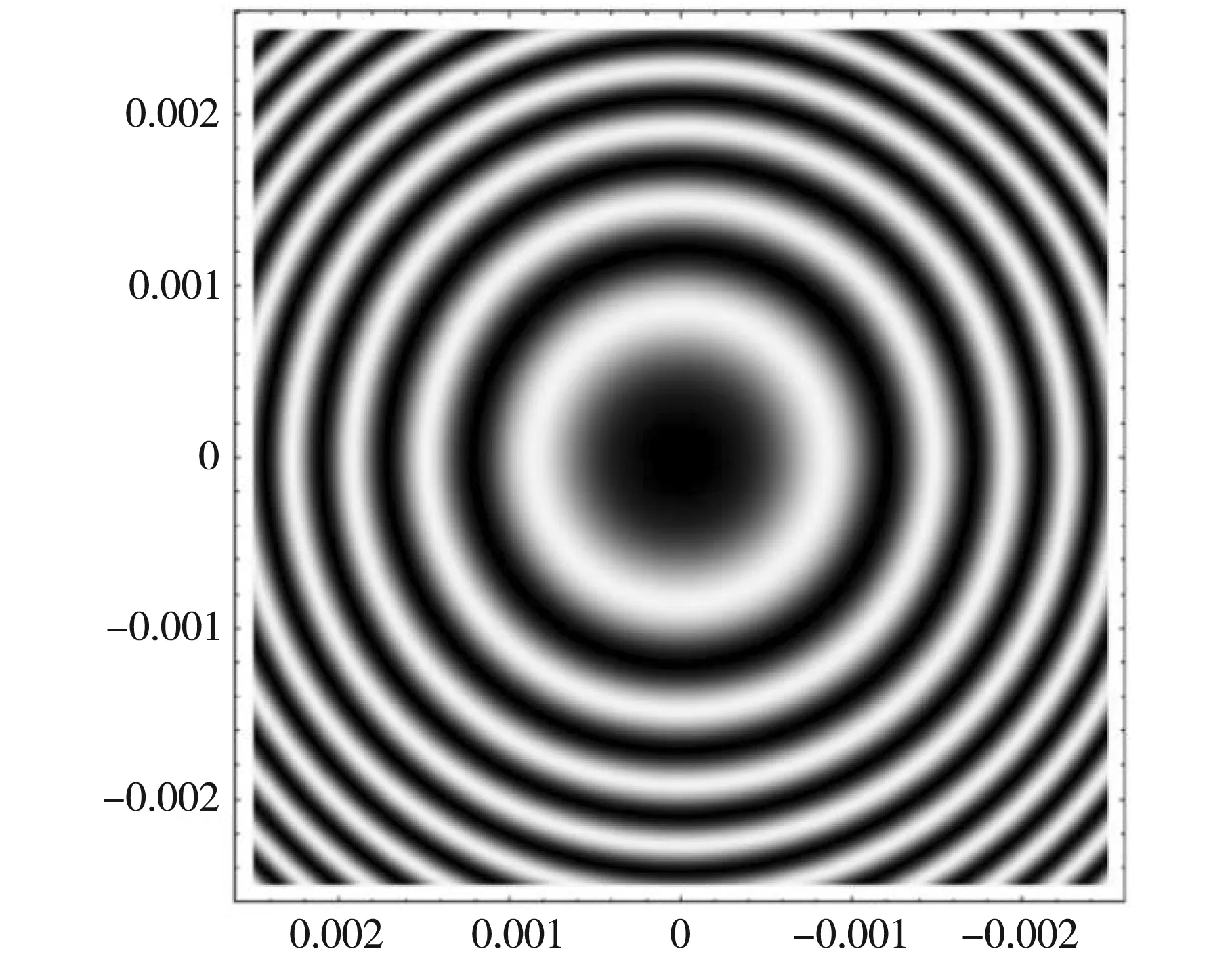
(a) 组合透镜下牛顿环干涉图样

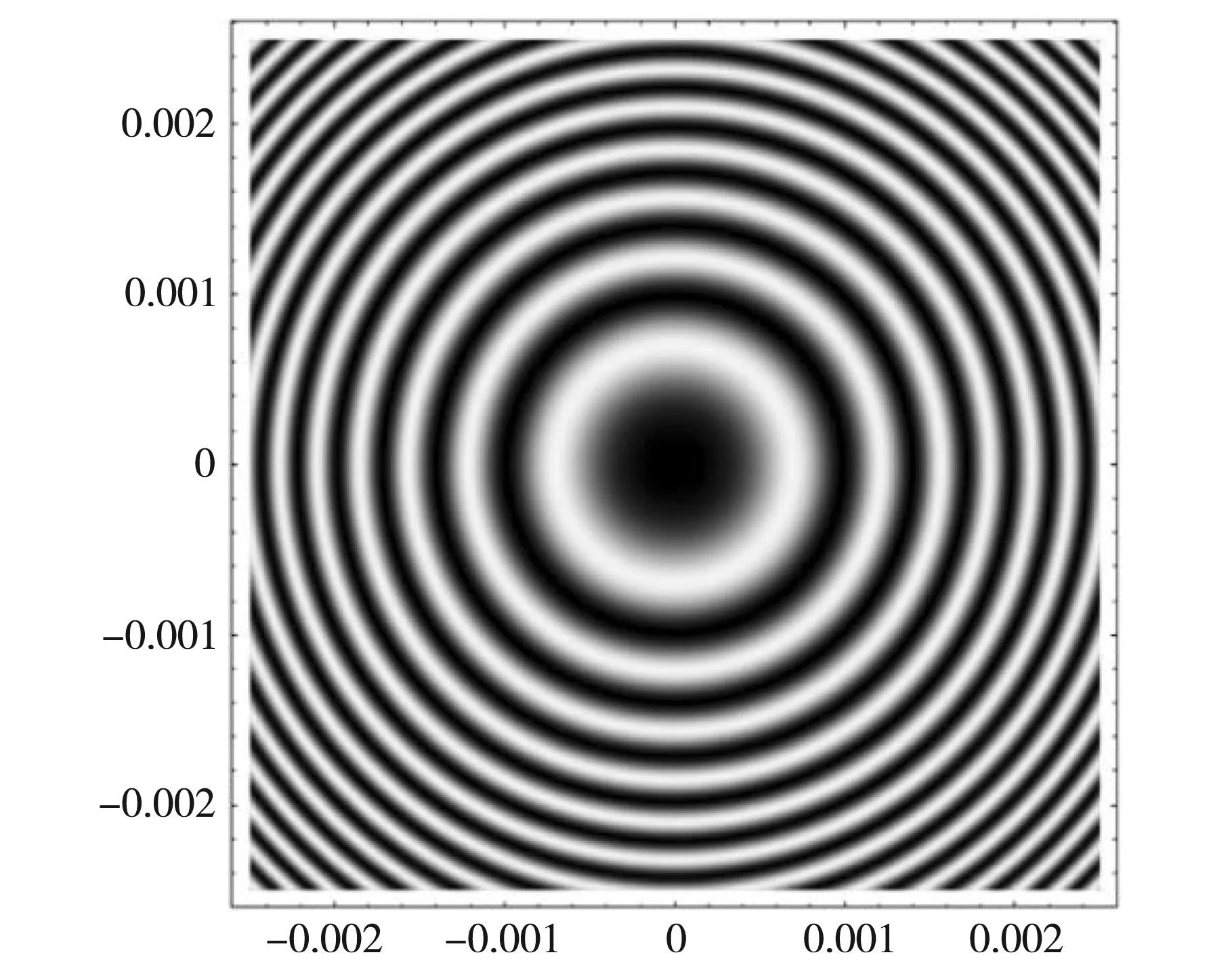
(a)牛顿环干涉图样

当a=0.8时的光强分布曲线如图6所示，在区间(-0.002 5,0.002 5)内明环的最高干涉级为6级，暗环的最高干涉级为7级。与图5相比较，图6的牛顿环R不变，a值增大0.5，亮环和暗环的最高干涉级均大于图5，相邻的明环与暗环间距更小，干涉条纹更密集。

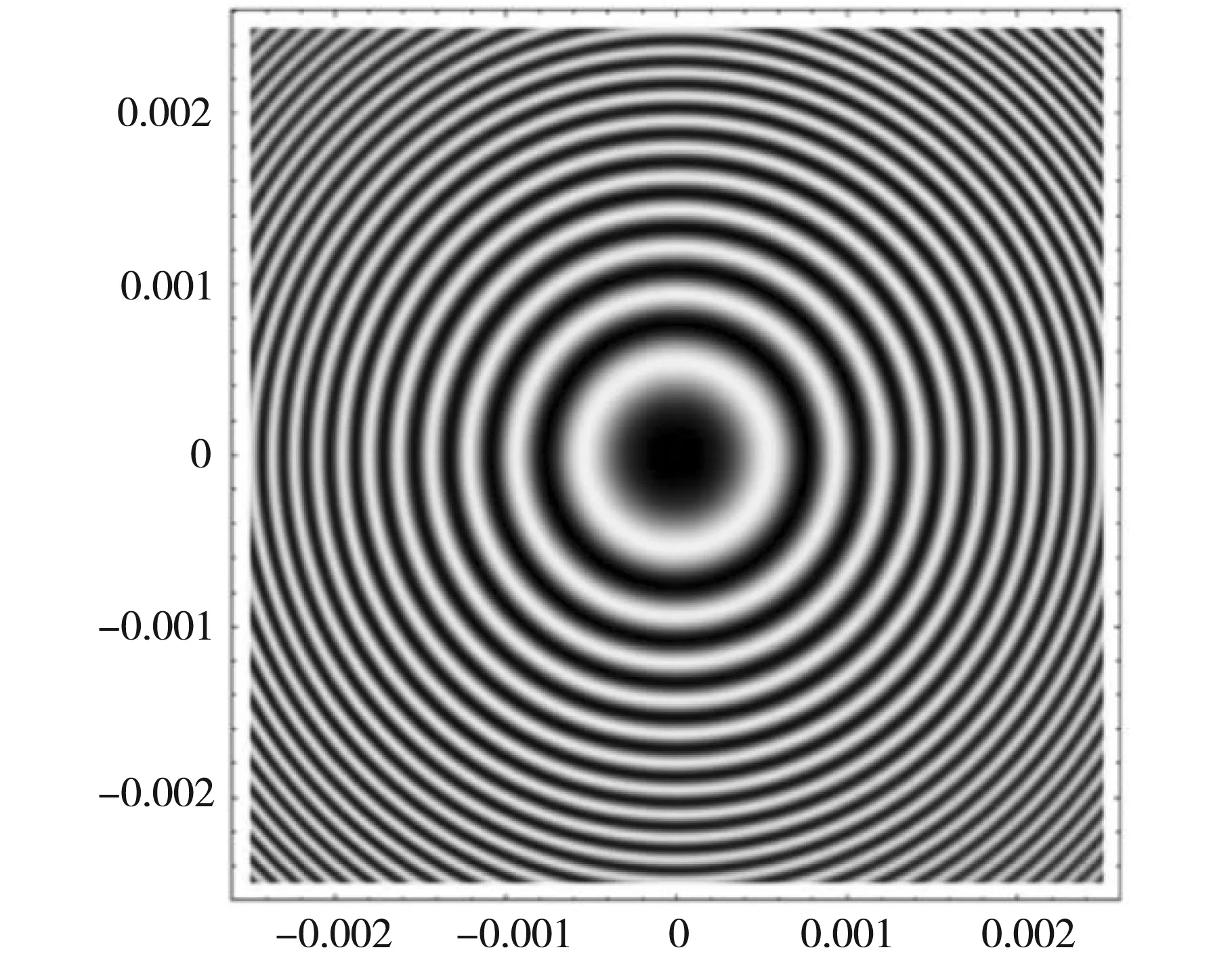
(a)牛顿环干涉图样

当a=1时光强分布曲线如图7所示，在区间(-0.002 5,0.002 5)内明环的最高干涉级为11级，暗环的最高干涉级为11级。三组图R值均相等，与图5、图6相比，图7的牛顿环a值最大，在相同的区间内，图7的干涉条纹数最多，条纹间距最小，条纹最密。

所有画出的图样都是圆形，与普通牛顿环图样的差别在于圆环的间隔不一样。根据上图可知，当入射光的波长和曲率半径R不变时，随着二次函数斜率a的增大，组合透镜下牛顿环的干涉条纹间距减小，干涉条纹越密集。

3.2 当a固定改变组合透镜的曲率半径R所得的干涉图样和干涉光强分布曲线

仍旧使用钠黄光，波长λ=589 nm，当固定二次函数的斜率a=0.25时，改变曲率半径R的值，根据(12)式可以得到如下图的干涉图样和干涉光强分布曲线，如图8、图9和图10所示。

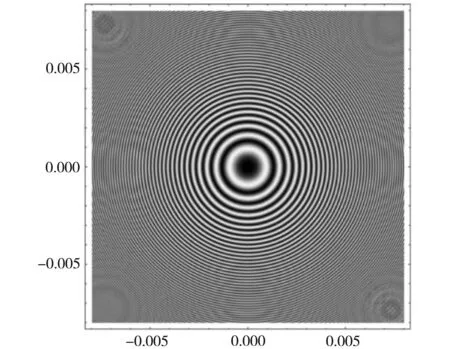
(a) 牛顿环干涉图样

当r=1.2 m时,利用Mathematica模拟牛顿环干涉所得的图样以及光强分布曲线如图8所示，在(-0.008,0.008)范围内亮环的最高干涉级为36级，暗环的最高干涉级为37级。

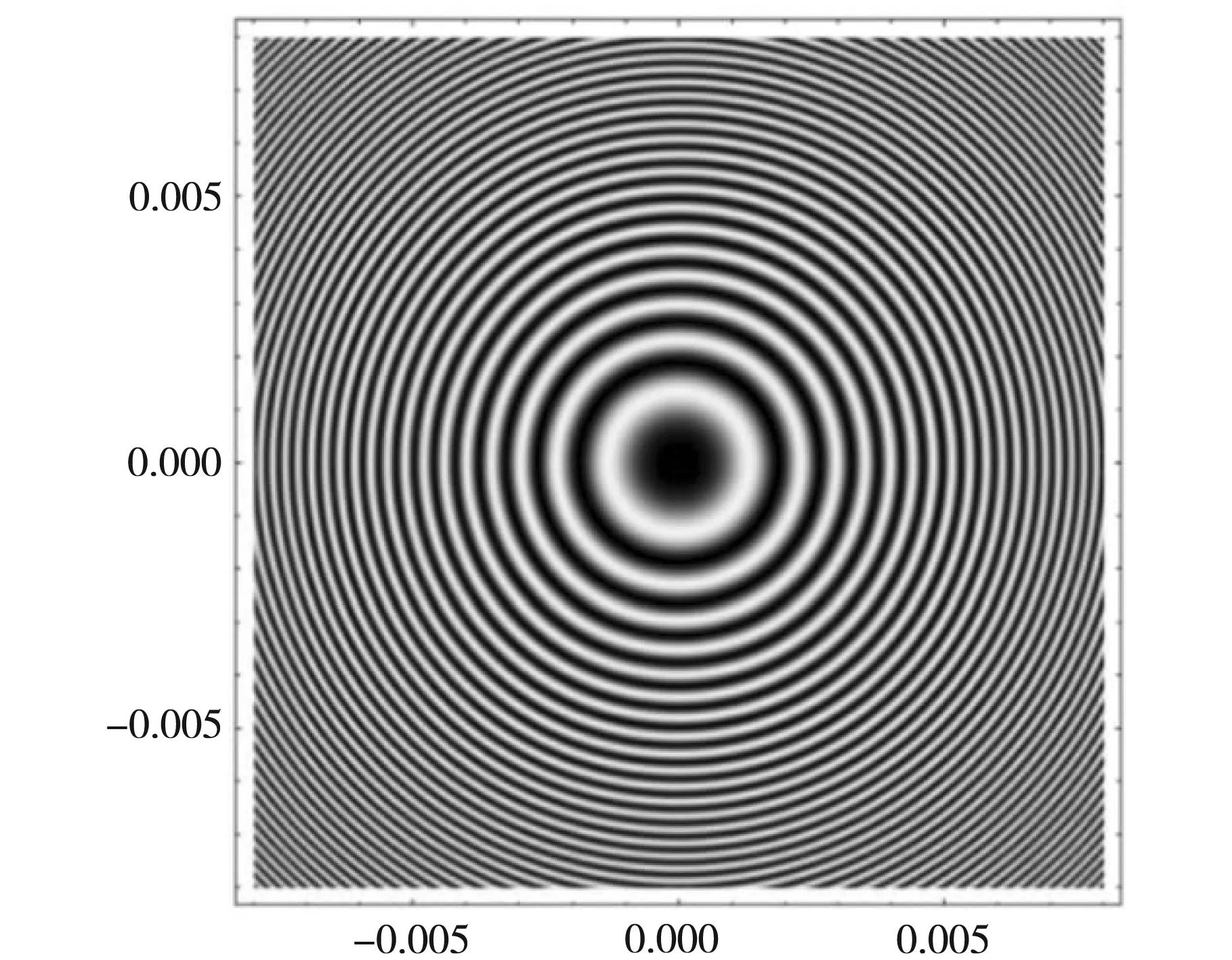
(a)牛顿环干涉图样

当r=1.5 m时，图样及光强分布曲线如图9所示，在(-0.008,0.008)区间内明环的最高干涉级为18级，暗环的最高干涉级为19级。与图8相比，图9的牛顿环a值并无改变，R值减小，在相同的范围内，干涉条纹间距增大，条纹变稀疏。

(a)牛顿环干涉图样

当r=1.8 m时,所得的图样以及光强分布曲线如图10所示，在区间(-0.008,0.008)内明环的最高干涉级为6级，暗环的最高干涉级为7级。在a值不变的情况下，图10牛顿环R较图8、图9最大，相同的区间内，明环和暗环的最高干涉级数最小，干涉图样中干涉条纹的间距最大，条纹分布最疏。

根据以上三组图可知，当入射光的波长和二次函数斜率a不变时，随着曲率半径R的增大，组合透镜下牛顿环的干涉条纹间距增大，干涉条纹越稀疏。

3.3 比较不同系数a下的干涉光强分布图并得出结论

将普通牛顿环的光强图与组合透镜下的牛顿环的光强图做对比分析更有意义。当a=0时我们讨论的组合透镜完全回到通常牛顿环的情况。

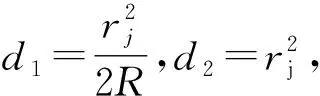
图11 普通牛顿环干涉光强分布图与当a=1时，组合透镜下的牛顿环光强分布图

同理，由公式(12)可画出当a=1，r=1 m和a=2，r=1 m时的光强分布图，如图12所示，在同一区间范围内，组合透镜在a=2时的明环数比a=1多，由光程差公式(11)得：

所以可以计算出第j级明环的半径

(13)

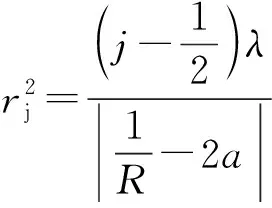
(14)

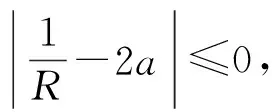
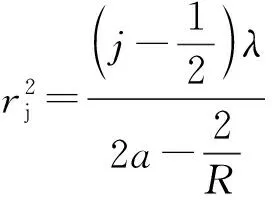
(15)

即

(16)

同理可得第j级暗环半径

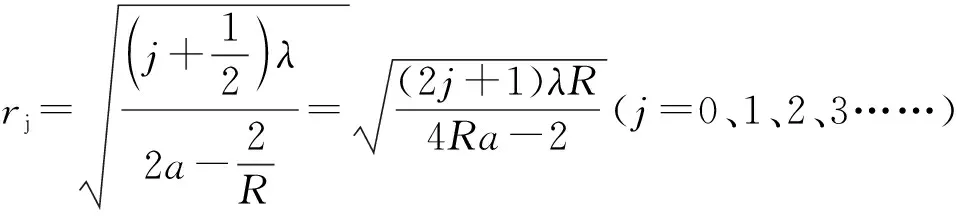
(17)

相邻的明环和暗环间距为

(18)

当干涉级数j不变时，二次函数斜率a越大，相邻的明环和暗环间距ej越小，所以在同样的区间范围内，a越大，所产生的牛顿环干涉环数越多，干涉条纹越密集，如图12所示。此时我们讨论的组合透镜牛顿环与正常牛顿环图样不重合。

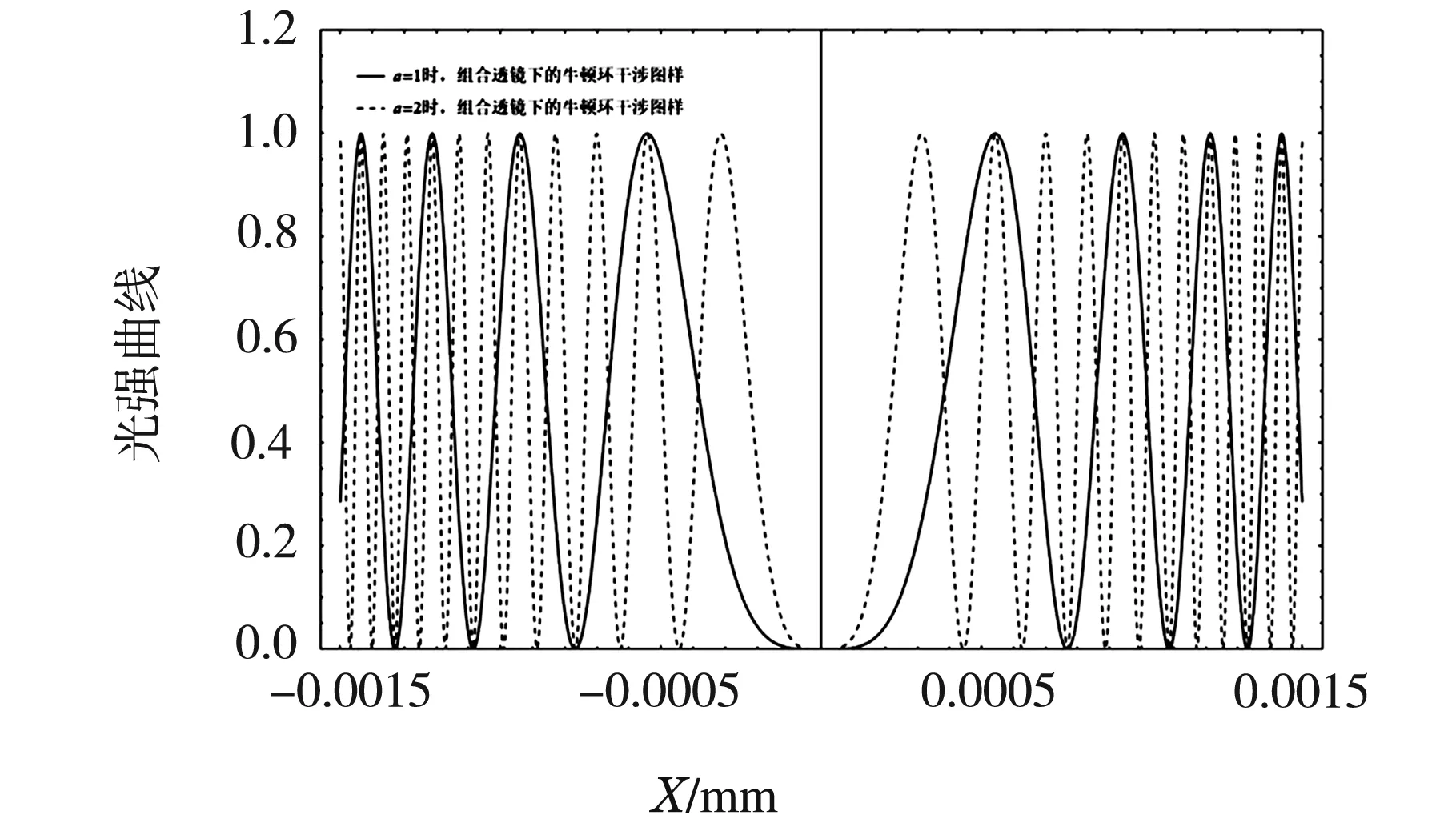
图12 当a=2时，组合透镜下的牛顿环光强分布图与当a=1时，组合透镜下的牛顿环光强分布图

4 结 语

推导出由旋转抛物面和球面构成组合透镜下广义牛顿环的干涉公式，并利用Mathematica模拟组合透镜下的牛顿环的干涉图样以及光强分布图，发现组合透镜下的牛顿环干涉图样仍旧呈圆环状，因为旋转抛物面和球面直接形成空气劈尖，根据等厚干涉原理厚度相同对应同一级干涉条纹，根据旋转对称性可知组合透镜下的牛顿环干涉图样也是圆环。通过数值模拟可以看出，变形牛顿环的干涉图样与二次函数斜率a以及曲率半径R取值有关，a值越大，同等条件下的牛顿环干涉条纹间距越小，干涉条纹数越多；R值越大，同等条件下牛顿环干涉条纹间距越大，干涉条纹数越少。