基于Abaqus模拟分层仿生梁的弯曲性能

余江滔，崔 璨，叶俊宏，张江頔

（同济大学结构防灾减灾工程系，上海 200092）

建筑3D打印具有施工快、无需模板和劳动力等优势.混凝土分层喷挤叠加方法［1］是目前常见的建筑增材建造技术，但其存在层间薄弱，在荷载作用下易出现相对滑移、错动以及打印材料必须与钢筋协同工作才能满足所需力学性能等短板，因此建筑3D打印仍停留在轮廓工艺［2］阶段.

贝壳珍珠母由大量脆性矿物片状文石和少量有机质构成，其拉伸强度比普通文石高3～5倍（超过100 MPa），极限延性高约10倍（达到1%），断裂能高近1 000倍.受贝壳珍珠母文石层独特的“砖-泥”结构［3-9］启发，本文拟通过模仿贝壳珍珠母的多级分层结构来对混凝土材料进行分层组装，以期对混凝土材料实现增强增韧.工程用水泥基复合材料（ECC），具有较高的拉伸强度和超过2%的延性［10-14］，本团队研制了平均拉伸应变能力在6%～12%的ECC，堪比GB50010-2010《混凝土结构设计规范》和GB5011-2010《建筑抗震设计规范》中关于钢筋延伸率的需求，并将其命名为超高延性混凝土（UHDC）［15-18］.

针对传统混凝土材料抗拉性能不足以及与建筑3D打印层间黏结薄弱的问题，本文仿照贝壳珍珠母多级、有序的分层形式，以UHDC为分层组装基础材料，通过分层并在层间添加人工分隔，初步实现了多级分层组装结构，将贝壳珍珠母的增韧方式赋予受弯构件；利用黏性内聚单元和塑性损伤模型，对6种梁（含4种分层仿生梁）进行数值模拟，观察裂缝分布，对比试验与模拟的荷载-挠度曲线，分析裂缝开展、承载能力、变形能力、应力分布和层间滑移等，探究分层仿生梁力学性能与分隔/连接尺寸的关系.本研究可为后续合理设计分层仿生梁及建筑3D打印的工程实践提供参考依据.

1 仿生设计

天然贝壳珍珠母破坏时会出现不同层间裂纹偏转和矿物桥断裂.笔者所在团队曾通过在梁厚度方向上分层浇筑UHDC，在层间放置沿梁长方向间隔开孔（即开孔与不开孔交替布置）的聚氯乙烯（PVC）薄膜，制备了分层仿生梁.其中PVC不开孔区域的UHDC相邻层被分隔开来，诱导加载时裂缝沿层间发展并偏转；PVC开孔区域的UHDC相邻层相连接，以阻止层间界面贯穿裂纹出现.通过四点弯曲试验初步证明了分层仿生梁受弯可实现层间裂纹偏转、裂缝分叉和矿物桥剪断等［19］.

本文基于Abaqus进行了一系列UHDC梁的数值模拟及分析，包括整浇梁（CB）、层间无PVC薄膜的分层不分隔梁（LWSB）以及分层仿生梁（BSB）.分层仿生梁在每层PVC薄膜上进行开孔分隔，根据分隔尺寸x与连接尺寸y是否相等分为等距分层仿生梁和不等距分层仿生梁，其中：等距分层仿生梁为等距离开孔，x/y分别为5/5、10/10、20/20，分别记为BSB5/5、BSB10/10、BSB20/10；不等距分层仿生梁为不等距开 孔，跨 中x/y＝10/10，跨 端x/y＝10/20，记 为UBSB.BSB10/10的PVC分隔示意图见图1.梁的尺寸为500 mm×100 mm×100 mm，分层仿生梁在厚度方向上共10层，每层高度为10 mm；梁受四点弯曲荷载，净跨为450 mm，加载点为三分点.

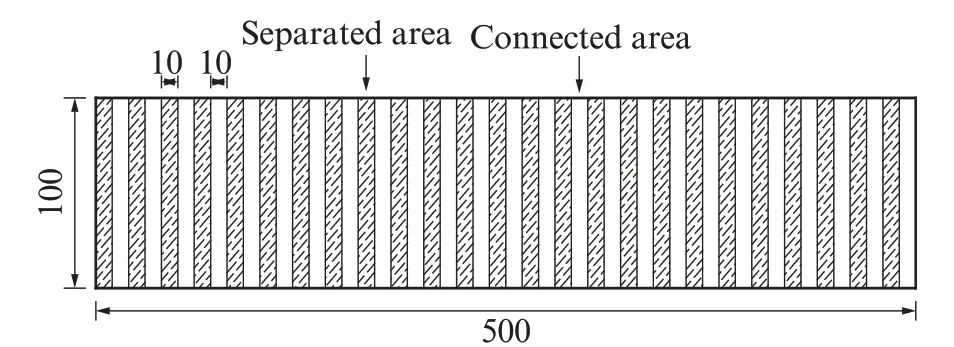
图1 BSB10/10的PVC分隔示意图Fig.1 PVC partition diagram of BSB10/10（size：mm）

2 Abaqus模型

2.1 几何模型的建立

采用Abaqus进行模拟.考虑受力特征，建立平面应力状态的二维模型，在分层仿生梁的层间连接处设置厚0.1 mm的黏性内聚单元（cohesive element）模拟连接.UHDC为CPS4R单元，黏性内聚单元为COH2D4.不等距分层仿生梁Abaqus模型立面图见图2.

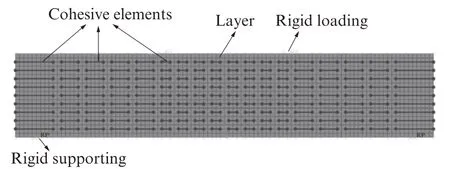
图2 不等距分层仿生梁Abaqus模型立面图Fig.2 Elevation view of Abaqus model of UBSB

2.2 UHDC本构关系模型

混凝土塑性损伤（CDP）模型可以描述材料的非弹性行为和材料断裂过程中发生的不可逆连续介质损伤.UHDC本构关系采用CDP模型，其参数为：UHDC弹性模量取20 GPa；泊松比为0.2；膨胀角取30°；偏心率为0.1；双轴极限抗压强度与单轴受压极限强度之比fb0/fc0为1.16；第2应力不变量之比K取0.667；黏性系数取0.000 5.

考虑弹性段、强化段和峰值应力后的软化，本文UHDC受拉本构关系采用Han等［20］提出的三折线模型.通过材料力学性能试验测得UHDC的受拉开裂应力σcr为3 MPa，受拉开裂应变εcr为0.02%，峰值拉应力σtp为8 MPa，峰值应变εtp为9.00%，彻底失效时拉应变εtu为15.50%.受压本构关系采用徐世烺［21］提出的应力-应变关系，考虑纤维的约束作用和20%残余强度，上升段为二次抛物线，下降段为双折线.通过材料力学性能试验测得UHDC的峰值压应力σpeak为48 MPa，峰值压应变εpeak为0.63%，残余强度为0.2σpeak，对 应 应 变εc为2.00%，极 限 压 应 变εcu为3.00%.

2.3 黏性内聚单元失效模型

选择Abaqus中的Traction-separation模型描述黏性内聚单元的失效；选用Maxs Damage描述初始损伤；采用基于Energy的损伤演化规律描述黏结层性能变化.本构模型为双线性模型，确定最大牵引力、最大牵引力对应位移与损伤失效位移后，可计算出黏性内聚单元的模量和断裂能.在Abaqus中设置最大牵引力、模量和断裂能分别为4 MPa、40 GPa和4 000 N/m，模量输入值为计算值的10倍.

2.4 相互作用与加载方式

UHDC层与黏性内聚单元之间采用绑定约束.层间分隔处为接触，法线方向为“硬”接触，切线方向用罚函数定义摩擦，摩擦系数为0.02.支座处设解析刚体，模拟铰支座；加载点处同样设解析刚体.加载方式采用位移加载.

3 Abaqus模型计算结果及分析

3.1 破坏时裂缝发展

图3给出了不同梁的裂缝开展图，各分图中的上图为真实试验裂缝示意图，下图为模拟裂缝分布.由图3可见，梁的模拟变形形态及裂缝与试验结果基本吻合，说明模拟结果可信.观察模拟裂缝：整浇梁仅在跨中出现1根向上延伸的主裂缝；分层不分隔梁在纯弯段均分布大量裂缝，剪弯段保持较好的完整性；BSB5/5和BSB10/10的裂缝分布相似，在加载点下方出现较多裂缝，跨中区域裂缝较少，同时相邻层分离；BSB20/20的裂缝更细密，在纯弯段和剪弯段均出现裂缝，纯弯段裂缝较少且纵向发展，而剪弯段裂缝沿层内横向延伸，出现了明显的层间滑移错动现象；不等距分层仿生梁的裂缝在纯弯区均匀分布，同时加载点下方出现横向裂缝，且支座至加载点出现了斜裂缝扩展.由此可见，尽管整浇梁较其余梁整体性更好，但其受弯时出现主裂缝即已破坏，并未完全发挥出UHDC的高延性和多裂缝性能；反观分层不分隔梁和分层仿生梁，其破坏时裂缝不局限于跨中某一点，而是出现大面积裂缝，如珍珠母般的多裂缝；而分层仿生梁成功诱导裂缝在发展过程偏转与分叉，出现了层间横向裂缝，从而提高了构件的变形能力.

图3 不同梁的裂缝开展图Fig.3 Crack development diagrams of different beams

3.2 承载力与跨中挠度分析

不同梁的模拟、试验荷载-跨中挠度（P-δm）曲线见图4，梁的最大承载力Pmax和极限跨中挠度δm，ult（90%极限荷载对应挠度［22］）见表1.由图4和表1可见：梁的荷载-跨中挠度的模拟曲线与试验曲线趋势一致，关键数值点接近，最大承载力误差均小于10%，极限跨中挠度误差均小于10%（除BSB20/20外），说明模拟结果可靠；整浇梁的模拟最大承载力为28.3 k N，分层不分隔梁和分层仿生梁的最大承载力均不低于整浇梁，且极限跨中挠度远大于整浇梁，这说明分层不分隔梁和分层仿生梁既具有等同整浇梁的承载力，又具有远大于整浇梁的变形能力；随着跨中挠度的增加，整浇梁的承载力在达到最大值后逐渐下降，而分层不分隔梁和分层仿生梁的承载力达到最大值后出现了类似钢材的强化平台，具有明显延性特征.将分层不分隔梁和分层仿生梁的受弯破坏分为3个阶段：弹性段、强化段和下降段.强化段承载力随跨中挠度增加存在较小波动.

由图4还可见：随着x/y的增大，等距分层仿生梁的最大承载力降低，极限跨中挠度增大；而不等距分层仿生梁的跨中部分连接尺寸小，易实现裂缝偏转与层间滑移，跨端连接区域大，保证了弯剪区具有足够的连接段，降低了滑移发生的可能性.结合表1可知：从模拟结果看，不等距分层仿生梁同时具有最高的最大承载力和极限跨中挠度；从试验结果看，其具有最高的最大承载力和次高的极限跨中挠度.综合考虑最大承载力与极限跨中挠度，不等距分层仿生梁的受弯性能最优.

图4 不同梁模拟及试验荷载-跨中挠度曲线Fig.4 Simulation and test load-deflection curves of different beams

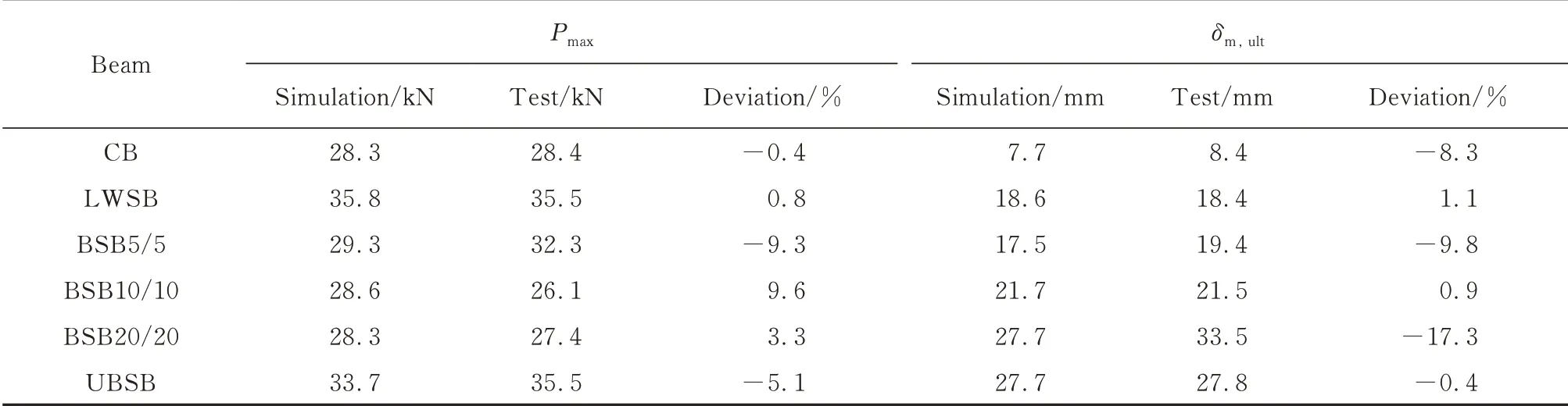
表1 不同梁的最大承载力与极限位移Table 1 Maximum load and ultimate deflection of different beams

3.3 最大主塑性应力分布云图

图5为不同梁的最大主塑性应力（SM.P）分布云图.由图5可见：与其他梁相比，整浇梁SM.P的最大值最小（7.705 MPa），较大SM.P（深色区域）主要分布在纯弯段；分层不分隔梁的SM.P较均匀地分布在纯弯和剪弯段，且受拉区高度高于整浇梁；从整体看，分层仿生梁的SM.P大于整浇梁和分层不分隔梁，其中BSB5/5和BSB10/10的SM.P最大值出现在加载点下方；与其他梁不同的是，分层仿生梁的应力分布出现明显的分层现象，这表明分层分隔形式有利于实现梁的应力扩散，使SM.P不仅分布于跨中截面，还分布在剪弯段，使梁承载能力得到较大程度的提升；分层不分隔梁的最终变形为弯曲型，最大应力在纯弯段；分层仿生梁变形趋向为梯形，其剪弯段受力较纯弯段大.综上，分隔削弱了层间黏结，且剪弯段属于复杂应力状态，因此同样的材料强度，剪弯段会先于纯弯段破坏，因此分层仿生梁承载力较分层不分隔梁低.

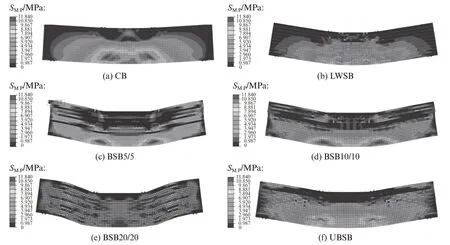
图5 不同梁的最大主塑性应力分布云图Fig.5 Cloud diagram of S M.P of different beams

3.4 层间滑移现象

沿梁高（d）提取剪弯段、加载点及纯弯段（跨中）3个截面的轴向位移（s）来分析层间滑移.不同梁的轴向位移见图6.由图6可见：整浇梁和分层不分隔梁的轴向位移曲线近似为直线，说明梁各层能够协同弯曲变形，受弯变形仍符合平截面假定；分层仿生梁在剪弯段和加载点处的轴向位移曲线为明显的锯齿状，层间位移出现突变，变形不再符合平截面假定.综上，普通混凝土梁的承载力计算方法不再适用于分层仿生梁，需要提出新的承载力计算方法.

图6 不同梁的轴向位移Fig.6 Axial displacement of different beams

4 结论

（1）通过设计超高延性混凝土（UHDC）分层仿生梁的分隔/连接尺寸，使分层仿生梁实现了主裂缝的偏转和分叉，并激发出更多裂纹，分层仿生梁层间会出现滑移错动，其变形不再符合平截面假定.

（2）UHDC分层仿生梁的最大承载力高于整浇梁，极限挠度远大于整浇梁，有稳定发展的强化变形过程，表现出明显延性特征；分层仿生梁耗能能力和韧性较整浇梁均有明显优势.

（3）本文利用数值模拟中的隐式算法进行分析，在计算过程中容易不收敛、效率不高，后续模拟可考虑更稳定的显式计算方法；可设计并试验更多分层分隔形式的梁，如何将分层分隔设计理念运用在3D打印梁的工程实践中也有待进一步探索.