基于图像统计的带预制缺陷混凝土破坏机理

2021-12-30孙浩凯郑新雨陈一铂

建筑材料学报 2021年6期

孙浩凯，高阳，郑新雨，陈一铂

（1.山东大学岩土与结构工程研究中心，山东济南 250061；2.山东大学齐鲁交通学院，山东济南 250002；3.石家庄铁道大学大型结构健康诊断与控制研究所，河北石家庄 050043；4.西南交通大学交通隧道工程教育部重点实验室，四川成都 610031）

由于施工方法不当、材料质量不佳、工艺操作不严等造成的混凝土结构缺陷，不仅影响美观，还会引发各种工程事故.例如：隧道衬砌因填充不足造成内部含有空腔、甚至背后脱空，由此造成空腔附近的拉应力集中，导致裂缝的扩展及掉块［1］.以往对混凝土缺陷的研究仅从宏观力学性能角度进行分析，忽视了非均质三相体及两两接触面对混凝土产生的不良影响.目前，采用扫描电镜、核磁共振、计算机断层扫描、声发射等技术探究混凝土细观尺度与宏观性能的联系成了研究热点［2-4］.从细观尺度分析缺陷混凝土的裂缝扩展机理，更能揭示裂缝扩展的本质.

研究表明，内部缺陷对混凝土力学性能影响显著.对其进行研究时不可或缺的步骤为内部预制缺陷，目前研究虽考虑了缺陷的影响，但未能真实反映混凝土缺陷在实际工程中的分布状态.预制混凝土初始缺陷的常用试验方法为：预埋圆形塑料管表征空洞［5］、安插薄钢板模拟初始裂缝［6］、添加引气剂预制孔隙［7］、预埋聚苯乙烯泡沫（EPS）颗粒模拟宏观缺陷［8］等.

数值模拟可以完成定量、定位、定型的前期模型设计，并完成在复杂工况下的结果分析，可操作性强、重复性高，因此数值模拟被广泛应用于细观混凝土性能研究.主要建模方法为：随机力学模型，用以表征混凝土力学性能［9-10］；随机骨料模型，用以代替混凝土内部结构［11］；等比例三维模型重构［12］；数字图像处理后的概念模型［13］.但由于目前试验设备及处理方法的不足，通过数值模拟所获得的数据缺乏力学试验验证［14］.

EPS颗粒具有疏水性强、强度低、密度低、性能稳定等特点，且因其优异的保温、隔热、隔震、减震、大变形和超轻等特点已在建筑行业得到广泛应用；通过数字图像处理获取混凝土内部的细观结构特征，突破了传统分析中因模型不准确引起的误差，可在不破坏试样的条件下实现试样的重构.综上，本文选择以EPS颗粒定量、定位表征混凝土内部宏观缺陷，以数字图像处理后细观结构特征表征概念模型，采用计算机断层扫描（CT）、声发射（AE）和数字图像处理（DIP）的建模技术，对内含EPS颗粒的预制缺陷混凝土在单轴加载下开裂的全过程进行研究.

1 试验

1.1 预制缺陷混凝土的制备

水泥采用42.5普通硅酸盐水泥；细骨料为天然河砂，最大粒径为2.36 mm；粗骨料为天然花岗岩，粒径为5～10 mm.按照C30强度等级制备混凝土，其中水泥、细骨料、粗骨料、自来水、高效聚羧酸减水剂的质量比为5∶8∶10∶2∶0.06.

通过0.053 mm线径的细绳将直径为20.0 mm的EPS颗粒固定在模具内部，以定量、定位地预制缺陷.细绳是由聚乙烯及尼龙材料在纳米技术下聚合而成，最大承载力为10 k N，远大于振动过程中EPS颗粒浮力.成型尺寸为100 mm×100 mm×100 mm的混凝土试件.试件标准养护（（20±2）℃，相对湿度RH95%以上）28 d.

1.2 测试方法

采用山东科技大学矿业与安全工程学院的NanoVoxel-2000系列CT扫描设备，最高分辨率为0.5μm，每个混凝土样品可获得1 024张1 270像素×1 270像素的二维CT切片.由于裂缝在三维空间内是薄的壳体结构，其萌生阶段宽度方向往往仅占1个体素大小，因此识别到裂缝的最小宽度为单个像素大小，宽度约为0.1 mm，并以此界定宏观裂缝与微观裂缝.

选用北京软岛时代公司研发的DS5全信息声发射信号，为了增大识别精度使用了6个探头，探头位置如图1所示（3、6号传感器在试件背面），其阈值水平设置为42 d B，前置放大器增益为40 d B，采样率设置为3 MHz，记录幅值、能量和计数等参数.传感器探针和压力机的压力头通过黏合剂固定在适当的位置，并通过断铅试验检查每个传感器的灵敏度，确保所有传感器的耦合均一致.

图1 声发射探头布置示意图Fig.1 Schematic diagram of sensor location distribution（size：cm）

使用CMT 3505型电子万能试验机测定试件的极限抗压强度（fu），加载采用位移控制，加载速率为0.1 mm/min.施加载荷前执行首次CT扫描，旨在验证预制缺陷方法，通过DIP获取混凝土内部的细观结构特征，建立“概念化模型”用于数值分析；声发射能量和振幅急剧增加时，执行第2次CT扫描，旨在观测早期的微裂缝萌生；达到极限抗压强度时，执行第3次CT扫描，观测最终的宏观裂缝及预制缺陷的发展.

2 结果及分析

2.1 单轴压缩下的宏观破坏行为

缺陷混凝土的荷载-位移曲线如图2所示.试件表面裂缝分布见图3.由图2可见：第Ⅰ阶段为0%fu～13.5%fu，此阶段为弹性阶段，相较于完整混凝土［6］，弹性阶段由30.0%fu降低至13.5%fu，可见预制缺陷导致前期较多微裂缝萌生，弹性变形包括初始空腔的压缩以及砂浆、骨料的弹性变形，并未出现宏观裂缝；第Ⅱ阶段为13.5%fu～100.0%fu，单轴抗压强度由完整混凝土的30.0 MPa降至16.5 MPa，降低了45%，可见内部缺陷对力学性能的影响显著，此时宏观裂缝首先出现在图3中箭头处，并集中在试块顶角处且扩展缓慢；第Ⅲ阶段为峰后阶段，此阶段裂缝扩展速度快，承载力急剧下降，顶部至底部生成大量宏观裂缝.

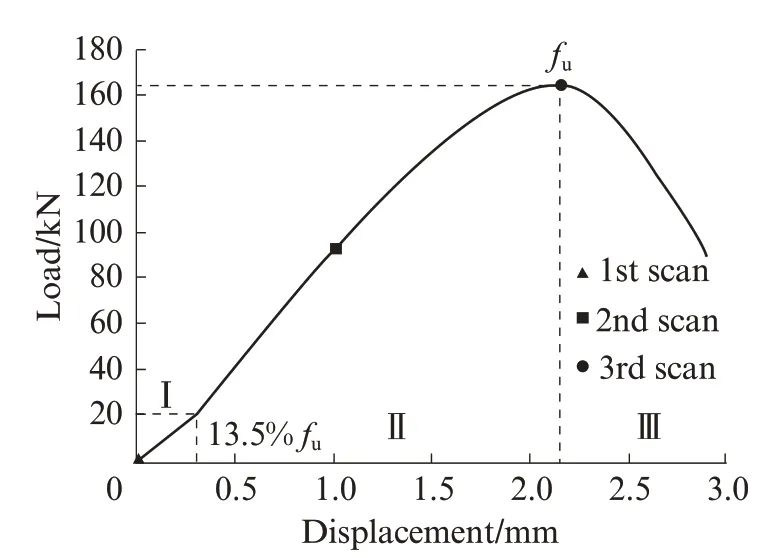
图2 缺陷混凝土的荷载-位移曲线Fig.2 Load-displacement curves of defective concrete

图3 试件表面裂缝分布Fig.3 Distribution of specimen surface cracks

2.2 基于声发射的裂缝扩展行为

结合声发射信号的3个重要特征参数（振幅、计数和能量），进一步研究了缺陷混凝土单轴压缩整个过程中的声发射特性.根据图4中的声发射测试结果对3个阶段进行分析：第Ⅰ阶段为弹性阶段，声发射信号的振幅及能量增长缓慢，表面仅有少量微裂缝产生，相较于完整混凝土［6］，缺陷混凝土接收到的声发射信号（声发射计数）较多（如图4（c）所示），验证了弹性阶段缺陷混凝土产生的微裂缝多于完整混凝土；第Ⅱ阶段，累计声发射能量增长速率逐渐上升，平均幅值虽低于第Ⅰ、Ⅱ阶段的过渡值，但仍高于第Ⅰ阶段，表明裂缝的扩展速率逐渐增大.总体而言，除了过渡阶段的跃迁外，振幅和能量在Ⅰ、Ⅱ阶段呈上升趋势；在阶段Ⅲ中，大量宏观裂缝的产生，使内部能量大量释放，振幅、声发射计数均减小.

图4 声发射测试结果Fig.4 Acoustic emission test results

相较于完整混凝土的声发射试验结果［6］，缺陷混凝土在前期加载过程中接收到的声发射信号较多，表明初始阶段中缺陷混凝土产生的微裂缝数量多于完整混凝土.这是由于内部缺陷的存在降低了混凝土的早期抗压性能.随着荷载的增加，新的微裂缝萌生、扩展，与旧的微裂缝连接形成裂缝体，使声发射计数、能量等均增长，但增长速率低于完整混凝土，这是由于前期缺陷混凝土已释放较多能量且承载能力远低于完整混凝土.在峰后阶段，声发射能量及振幅均增大，声发射计数逐渐减少，表明峰后阶段出现宏观裂缝.

2.3 基于图像统计的裂缝扩展行为

由于第2次CT扫描时，重构图像中未产生可识别的宏观裂缝（宽度大于0.1 mm），故未对第2次CT扫描图像作进一步分析.同时这表明在弹性阶段的声发射信号不是由宏观裂缝引起的，而是由砂浆与骨料的过渡区（ITZ）微裂缝萌生导致，因其尺寸约为微米甚至纳米级，通常可用扫描电子显微镜观测.

初始状态混凝土试件的CT扫描结果见图5.通过阈值分割技术将缺陷分割，并分别统计预制缺陷及初始孔隙（制作过程中虽进行充分振动，但仍会存留孔隙）体素大小、位置和形状等信息.统计得出初始孔隙数量和总体积分别为3 883个、2.50 cm3，预制缺陷总体积为33.45 cm3.由此可见，初始孔隙所占比例较小，对混凝土整体力学性能影响较小，因此不进行单独分析.预制缺陷位置、相应误差及半径误差见表1（混凝土的底面是XOY平面）.由表1可见，8个预制缺陷的位置误差均在5%以内，证明DIP技术可靠，半径产生误差的原因为EPS颗粒在压力作用下的微小变形，半径误差较小则证明缺陷预制方法合理.

表1 预制缺陷位置、相应误差及半径误差Table 1 Position，corresponding error of precast defects and error of radius

图5 初始孔隙和预制缺陷的分割Fig.5 Segmentation of initial voids and prefabricated defects

通过DIP技术量化裂缝并根据空间观测方向及破坏类型将裂缝分为2类，见图6（白色为Ⅰ型滑开型裂缝，黑色为Ⅱ类张开型裂缝）.由图6可见：2类裂缝相同的特点是均沿过渡区扩展；Ⅰ型裂缝特征为沿加载方向剪切破坏，数量少、长度长，对承载力影响较大；而Ⅱ型裂缝往往出现在水平缺陷投影面积最大的平面内，其特征为数量多、长度短；由于应力集中，裂缝往往出现在混凝土的角部及宏观缺陷附近；另外，在水平向距离混凝土边界较近处，扩展所需能量较少，易形成宏观裂缝.由图6（b）可见，EPS颗粒在荷载下沿水平向扩展（直径由20.0 mm扩展至21.1 mm），纵向被压缩（由20.0 mm缩小至18.8 mm），相较于其他薄弱部位，EPS颗粒中部的水平面在垂直与加载面方向上投影最大，同时距离边界较近，因此其水平扩展所需的能量少，当其应变大于极限弹性应变后试件发生屈服并形成裂缝.

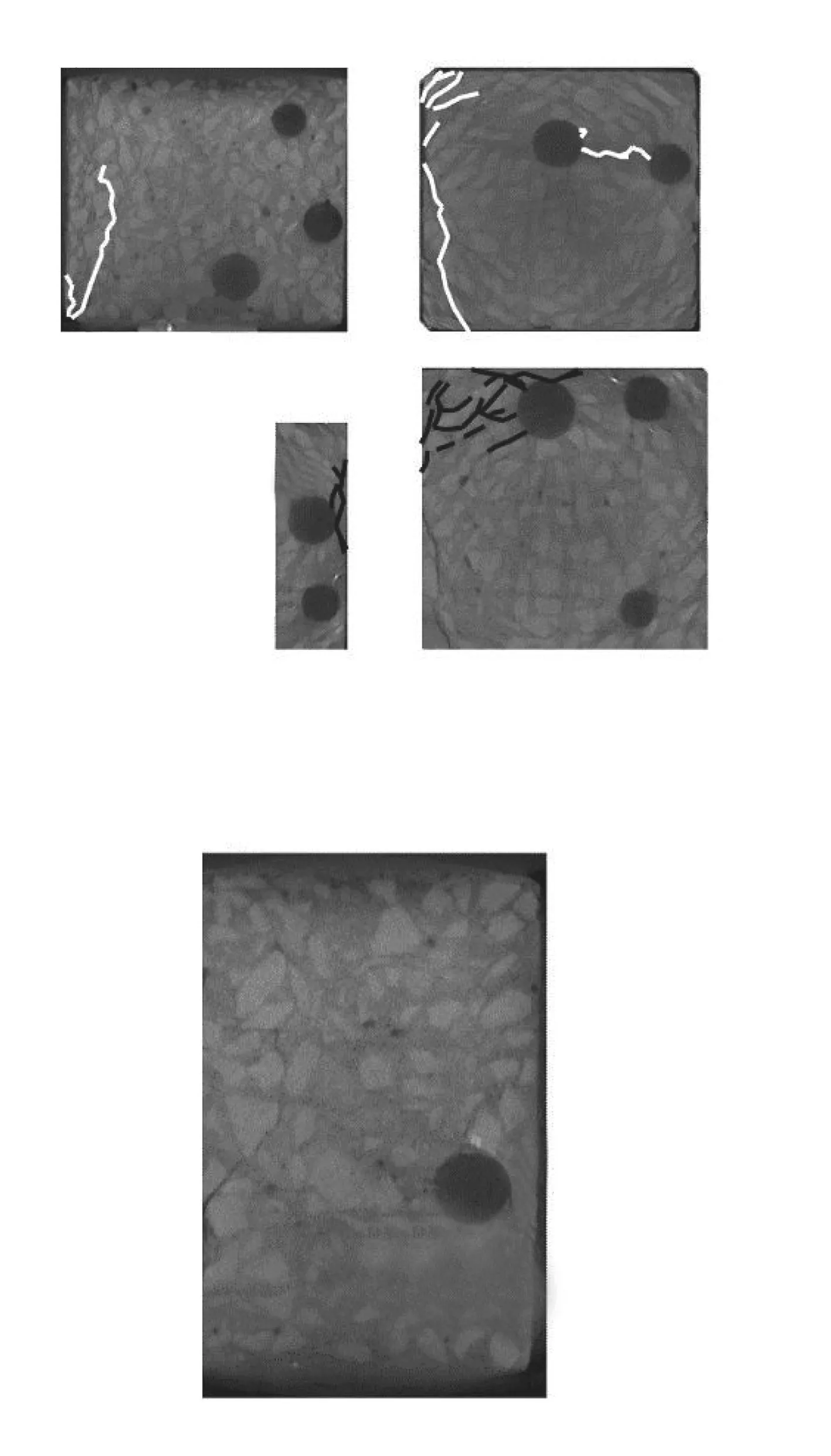
图6 第3次CT扫描中裂隙分类及EPS颗粒变形Fig.6 Crack classification and EPS particles deformation in the 3rd CT scan

3 数值模拟

为了深入研究缺陷混凝土的破坏机理，提出一种适用于精细化混凝土建模的实用方法，并可以将数值模拟所获得的数据进行力学试验验证.采用有效识别CT图像内骨料边界及特征概率信息的方法、等效随机多边形骨料放置方法、晶粒半径差异较大的细观离散元建模方法，实现基于传统骨料统计方法最大拟合程度的二维细观精细化模型重构.

3.1 数字图像处理方法

骨料集合的提取过程如图7所示，此处的机器学习训练种子可适用于混凝土试件所有切层图像，对此进行批处理.完成分割之后通常得到1幅包含前景和背景2个灰度值的二值图象，前景为“1”，背景为“0”，这里即骨料为1，砂浆为0.通过开发的“八邻域边缘追踪算法”将图像信息转化为数字信息.由于骨料边界像素点本身占据整数点坐标，多产生锯齿状边界，难以适用于数值建模，因此在八邻域边缘追踪算法基础上进行改进，通过Matlab开发了降噪算法，优化边界点的类型及数量如图7（g）所示，网格中黑圆点为需删除的噪点.

图7 骨料集合提取过程Fig.7 Extraction process of aggregates

3.2 改进的骨料几何特征概率统计方法

通过对所有优化后切片内骨料几何尺寸的提取（骨料的位置呈均匀分布，因此未对其进行统计），如：根据骨料顶点数量确定边数、根据骨料中心与顶点的距离确定等效半径及伸长率、根据最长轴与水平向夹角确定长轴角度等，并对骨料边数、伸长率、长轴角度与等效半径等参数进行概率统计.统计得到骨料边数和伸长率符合高斯分布，其概率分布参数结果见表2，其中σ、μ、R2分别表征数据分布的离散程度、集中位置和确定系数.长轴角度及等效半径分别在（-90°，90°）、（0.2 cm，0.6 cm）区间内符合平均分布.

表2 概率分布参数Table 2 Probability distribution parameter

3.3 基于概率统计的混凝土建模方法

3.3.1 骨料生成过程

每个骨料的形状可以通过将其边界轮廓转化为极坐标来建立，具体建立方法如下.

轴向角φi为：

式中：ηi为0～1的均匀随机数；n为边数；δ为不大于1的随机数。

为了保证骨料边界闭合，轴向角修正为：

骨料极轴长度r i通过下式计算：

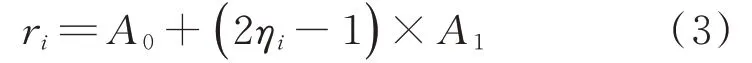
式中：A0为骨料平均粒径；A1为在平均粒径基础上的变化范围.

骨料边界点坐标x i、yi可由下式得出：

式中：x0i、y0i分别为整体模型边界范围的随机点；θi为边界点极角.

通过笛卡尔坐标系中的矩阵变化分别控制骨料的长轴角度与长度，使其分别与统计结果相同，长轴角度边界点坐标矩阵X′与原骨料边界点坐标矩阵X之间的转化关系为：

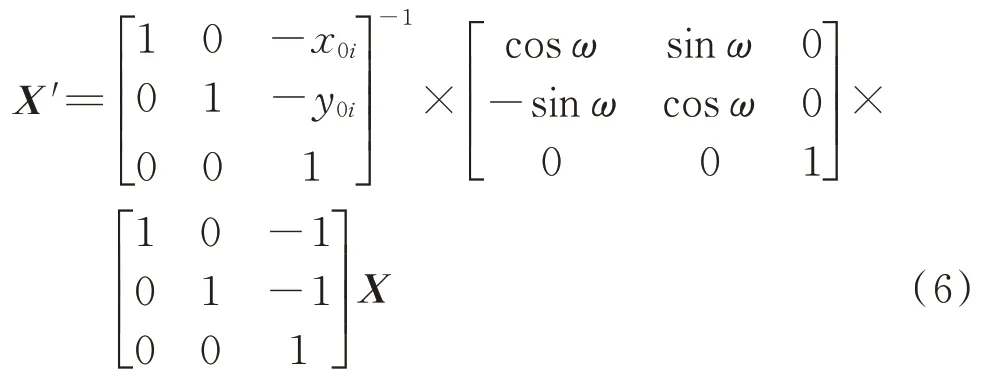
式中：ω为旋转角度.

长轴边界点坐标矩阵X″与原骨料边界点坐标矩阵X之间的转换仅为在旋转角度基础上乘以放大系数矩阵κ：

在［Ds，Ds＋1］级配中骨料的面积Aagg由下式计算：

式中：Ds、Ds＋1分别为当前计算的骨料范围中最小粒径和最大粒径；Aagg为当前计算的骨料面积；Dmin、Dmax分别为骨料的最小、大粒径；Acon为混凝土面积；Ragg为骨料与混凝土面积的比值；P为概率.

即可根据概率密度函数生成“概念化模型”.

3.3.2 GBM方法的改进过程

Grain-based method（GBM）是适用于Particle Flow Code（PFC）软件的精细化岩样建模方法.该方法根据岩石内晶粒的大小，生成一系列圆形颗粒，然后将相邻颗粒孔隙质心用线连接，生成多边形网络，导入块体离散元模型中，并在对应晶粒处赋予圆形颗粒相应参数.由于操作复杂且适用范围窄，GBM方法受到极大限制，很难适应中尺度及各种复杂情况下砂浆和骨料的建模，容易在较大的晶粒边界处出现锯齿状边界.

改进后的建模过程如图8（a）中Star-Method improvement-End段所示：首先在砂浆区域内，通过Matlab生成符合具体工程情况的随机离散点群；进一步以这些点为中心，在骨料边界外至混凝土边界内的区域内建立泰森多边形；将得到的泰森多边形边界及骨料边界导入数值模型中，并在相应区域赋予对应的材料属性.根据首次CT扫描图像得到的概率密度函数，建立数值模型如图8（b）所示.

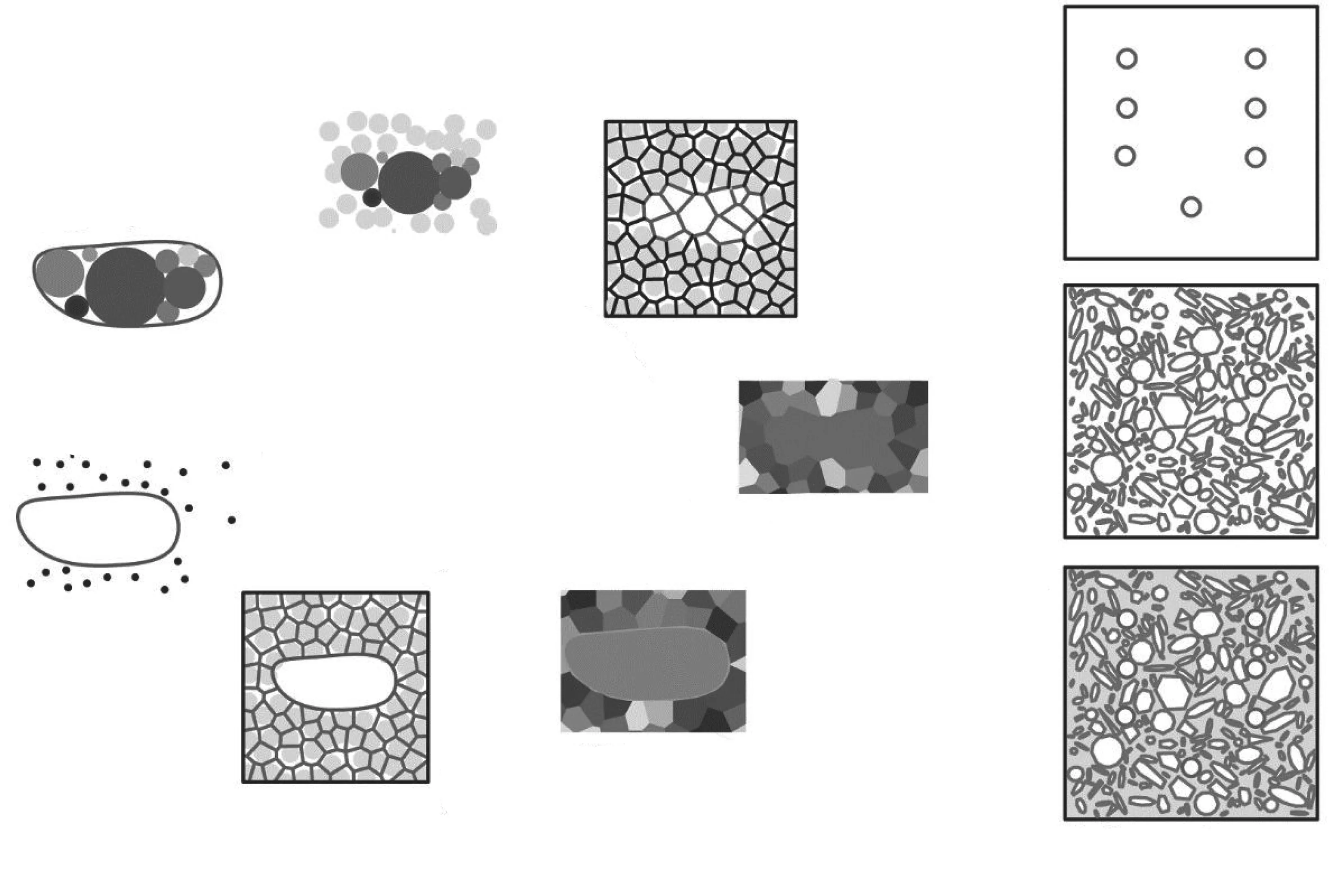
图8 建模过程对比及改进后模型生成步骤Fig.8 Modeling process comparison and improved model generation steps

3.4 缺陷混凝土建模及单轴压缩模拟

3.4.1 数值模型及模拟方案

在试件顶部以0.1 mm/min的恒定速率施加轴向荷载，参数标定方法与GBM方法相同，进行纯砂浆试块的单轴压缩试验及巴西劈裂试验以校订微观参数，最终确定的微观参数如表3所示.根据块体离散元软件中的极限破坏准则，当块体之间的应力大于张力或剪切力阈值时，将被视为AE事件，以此设计了“声发射”功能来捕获破裂事件，用于监测不同断裂形式（张拉、剪切）及断裂的长度，方向、数量和位置等信息，从而真实地显示破坏过程.

表3 微观参数Table 3 Microscopic parameters

3.4.2 数值模拟与试验结果对照分析

在极限抗压强度下，改进方法得到的宏观破坏效果见图9.由图9可见，模拟结果中混凝土共出现了3种类型的裂缝：（1）混凝土右上角出现网状、长度较短裂缝；（2）混凝土左侧出现沿加载方向贯穿劈裂的宏观裂缝，长度较长；（3）混凝土内两预制缺陷之间出现贯穿裂缝.3种裂缝均能较好地反映重构CT图像中的裂缝种类.数值模拟与试验测得的带预制缺陷混凝土最大抗压强度分别为15.75、16.50 MPa，误差小于5%，验证了基于改进GBM方法所得模拟结果的可靠性.

图9 改进方法得到的宏观破坏效果Fig.9 Macroscopic damage based on the improved method

在模拟过程中分别对砂浆中的张拉裂缝、剪切裂缝和砂浆-骨料过渡区的张拉裂缝、剪切裂缝进行量化分析，结果如图10所示.根据以上4类裂缝的相对数量关系将整个加载过程细分为3个阶段：（1）0%～19.5%极限抗压强度阶段，过渡区生成大量剪切裂缝，且砂浆之间接触面几乎未发生破坏，这是由于过渡区的力学性能较弱，变形较小，对宏观性能未产生显著影响，同时这也验证了在第2次CT扫描期间未能看到显著变化，加载初期接收到的声发射信号来源于过渡区；（2）19.5%～61.7%极限抗压强度阶段，随着荷载的增加，剪切裂缝延伸至砂浆间应力集中处，导致少量微裂缝产生，此时变形大大增加，但裂缝的形状基本保持稳定；（3）61.7%～100.0%极限抗压强度阶段，砂浆接触面开始大量出现破坏，而过渡区不再大量出现新的破坏面，此时，砂浆接触面的剪切裂缝数量逐渐超过过渡区的张拉裂缝数量.这是因为砂浆接触面的力学性能比过渡区的力学性能强，且砂浆接触面的数量远大于过渡区接触面数量.这验证了细观模拟与力学试验的一致性，又对试验结果进行补充.

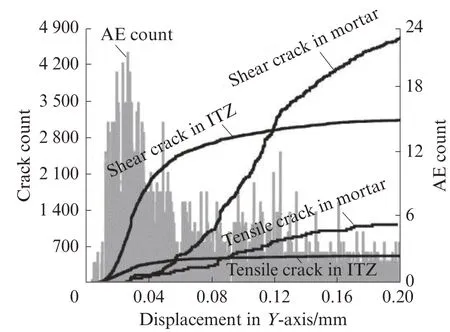
图10 裂缝量化分析Fig.10 Crack quantitative analysis

3.5 应用

建立一套适用于大型混凝土结构的精细化数值模拟方法更具现实意义.基于上述方法，通过在混凝土结构不同部分钻孔采样，进行CT、数字图像处理、归纳骨料和孔隙的分布特征、即可建立反映混凝土内部真实细观结构的数值模型.其中敏感部分可进行精细化建模，其余模型仍建立在宏观尺度上，进而在不同应力条件下进行数值分析以获得结构性能，这对大尺度高精度建模具有指导意义，可实现结构的归一性［15］，使复杂的工程分析变得简单高效.此处展示隧道衬砌的拱顶细观模型，建模流程如图11所示.