定向钢纤维增强地质聚合物复合梁的抗弯性能

张伟杰，谢子令，周华飞

（1.温州大学建筑工程学院，浙江温州 325000；2.浙江工业大学土木工程学院，浙江杭州 310000）

地质聚合物的概念首先在20世纪70年代提出［1］，由于其具有二氧化碳排放量低、强度高、硬化快等特点，因此被认为是一种更清洁的材料［2］.国内外学者讨论了不同原料［3］、养护制度［4］对于地质聚合物力学性能的影响等.与许多水泥基材料类似［5-8］，地质聚合物存在脆性大，韧性差等缺陷，掺入钢纤维［9-11］是解决这一问题的重要途径.然而，关于钢纤维取向和分布对于地质聚合物力学性能影响的研究鲜有报道.

钢纤维取向对基体的增强效果起到了关键作用.慕儒等［12-14］制备了定向分布钢纤维水泥砂浆，研究表明，与乱向分布钢纤维相比，定向分布钢纤维增强水泥砂浆的抗折强度、弯曲变形能力等均得到显著提高.由于全截面钢纤维增强混凝土中的钢纤维用量大且造价过高，因此国内外学者对部分钢纤维增强混凝土做了一定研究，结果表明，在构件的受拉侧加入部分钢纤维是经济有效的［15-16］，并且存在一个最优的钢纤维层厚度，使得部分钢纤维增强混凝土的增强、阻裂效果可以近似达到全截面钢纤维增强梁的效果［17-20］.

鉴于国内外对于部分定向钢纤维增强地质聚合物的研究鲜有报道，本文利用磁场实现钢纤维定向化分布并选取钢纤维层厚度（hf）为变量，制备不同纤维层厚度的定向钢纤维增强地质聚合物复合梁，对其抗弯性能进行了试验研究与分析.

1 试验

1.1 原材料

砂采用中砂，细度模数2.3.粉煤灰采用温州某火力发电厂产Ⅱ级粉煤灰，其中的SiO2和Al2O3含量（质量分数，文中涉及的含量、组成等除特别注明外均为质量分数）分别为56.74%和24.59%.激发剂由16 mol/L的NaOH溶液与水玻璃溶液按质量比1∶3混合而成，其中水玻璃溶液密度为1.35 g/cm3、模数为3.3，主要成分SiO2、Na2O和水的含量分别为27.9%、7.9%、64.2%.超细镀铜钢纤维直径为0.2 mm，长度为20 mm，抗拉强度为2 850 MPa，密度为7.8 kg/m3，掺量（体积分数）为1%.钢纤维增强地质聚合物配合比见表1.

表1 钢纤维增强地质聚合物配合比Table 1 Mix proportion of steel fiber reinforced geopolymer kg/m3

1.2 试件制备

制备了1组无纤维地质聚合物的空白对比试件（R00）、1组全截面杂向纤维增强复合梁对比试件（R100）、6组定向钢纤维层厚度不同的复合梁试件（DX，其中D表示定向，X表示钢纤维层厚度）.各组三点弯曲梁试件尺寸均为100 mm×100 mm×400 mm.

采取分层方式制备定向钢纤维增强地质聚合物复合梁试件，具体制备工艺如下：首先称取一定质量的砂、粉煤灰和钢纤维，将其倒入搅拌机中，干拌5 min；随后加入一定质量的激发剂，再次搅拌5 min；最后，将拌和物倒入事先已标出不同高度的模具中，并在图1所示的磁场环境（实现纤维定向）中振动成型1 min，待下部成型的钢纤维增强地质聚合物初凝后（30 min左右），再浇筑上部不掺钢纤维的地质聚合物拌和物.在制备过程时，为防止下部钢纤维在二次振动成型过程中取向发生改变，二次振动成型仍在磁场环境中进行.

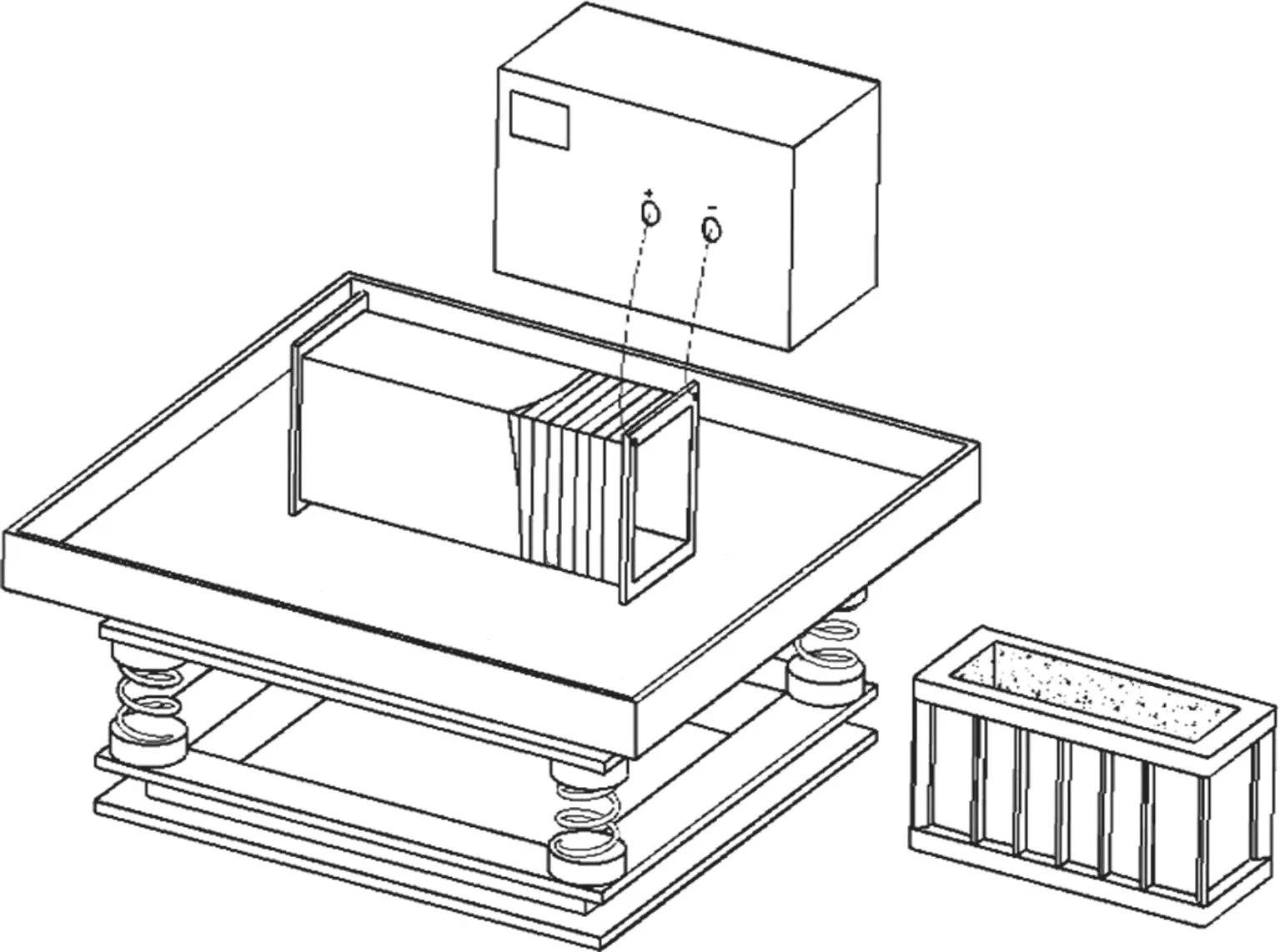
图1 定向钢纤维增强地质聚合物制备装置Fig.1 Preparation device of directional steel fiber reinforced geopolymer

为得到地质聚合物基体及定向纤维增强地质聚合物的立方体抗压性能，同时成型了1组无纤维地质聚合物的空白对比试件（A 0）、2组定向纤维增强地质聚合物立方体抗压试件（ADV、ADP）.3组试件尺寸均为70.7 mm×70.7 mm×70.7 mm.

上述所有试件均在60℃条件下养护24 h后拆模，再室温养护7 d后进行三点弯曲试验和立方体抗压试验.

1.3 试验设备与方法

三点弯曲试验在深圳市新三思计量技术有限公司产WDW-A型电子万能试验机上进行.最大载荷为50 k N，加载跨距为300 mm，利用挠度计记录跨中挠度，加载速率为0.1 mm/min，每组测试3个试件.三点弯曲试验加载示意图见图2.

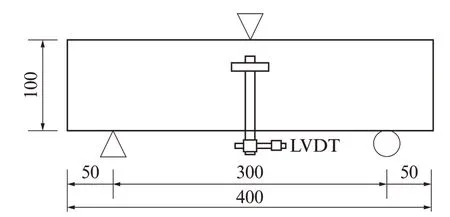
图2 三点弯曲试验加载示意图Fig.2 Schematic diagram of three point bending experiment（size：mm）

立方体抗压试验在上海华龙测试仪器有限公司产WAW-600型微机控制电液伺服万能试验机上进行，最大载荷为600 kN，加载速率控制为2 mm/min，每组测试3个试件，抗压强度值取其平均值.对于定向钢纤维试件，分别进行2种加载方向试验：一种是加载方向与纤维取向垂直（试件编号为ADV）；另一种是加载方向与纤维取向平行（试件编号为ADP）.不同钢纤维取向下立方体抗压试验加载示意图见图3.

图3 不同钢纤维取向下立方体抗压试验加载示意图Fig.3 Schematic diagram of cube compression test loading under different steel fiber directions（size：mm）

2 试验结果与分析

2.1 纤维取向

图4为R100组和D60组试件断裂后的截面图.由图4可见：R100组试件中的钢纤维分布杂乱；而D60组试件中的钢纤维分布方向基本一致，且钢纤维层厚度与试验设计较为吻合，表明试件制备结果良好，既能让钢纤维达到定向效果，也能得到理想的钢纤维层厚度；此外分层组试件的裂缝由底部开展，而不是沿交界面处破坏，证明试件制备方法具有可行性.

2.2 抗压性能

表2为试件7 d立方体抗压强度.由表2可见：无纤维地质聚合物的基体强度为19.36 MPa，而定向钢纤维增强地质聚合物的抗压强度表现出明显的各向异性.当钢纤维方向与加载方向垂直时，抗压强度达到21.96 MPa，较空白组提高了13%；而当钢纤维方向与受压方向平行时，抗压强度为14.15 MPa，较空白组降低了27%.

表2 试件7 d立方体抗压强度Table 2 Cube compressive strength at 7 d of specimens

为进一步探讨定向钢纤维增强地质聚合物抗压强度出现各向异性的微观机制，对比分析各组试件的破坏形态，见图5.由图5（a）可知，无纤维地质聚合物呈现明显的倒锥形破坏，这是由于在受压过程中，上下端面受到设备压板的摩擦力，从而产生环箍效应，随着压力的增大，试件中间部位受到摩擦力的影响最小，从而产生最大的横向位移，导致除上下端面外的4个侧面向外膨胀.由图5（b）可知，当钢纤维方向与加载方向垂直时，钢纤维能够抑制基体的横向变形，因此与钢纤维方向垂直的2个侧面受到约束效果，基本未发生膨胀，而与钢纤维方向平行的2个无约束侧面由于环箍效应仍发生膨胀，其抗压强度相较于无纤维地质聚合物有所提高.由图5（c）可知：（1）当钢纤维方向与加载方向平行时，由于钢纤维抑制横向变形的作用减弱，钢纤维对4个侧面基本上无约束作用，导致其破坏形态与无纤维地质聚合物类似；（2）在钢纤维与基体连接的界面处有更多的细微裂缝产生，表明钢纤维与基体连接的薄弱界面可能成为微裂缝产生源，进而导致其抗压强度相较于无纤维增强地质聚合物有所降低.

图5 试件立方体抗压试验破坏形态Fig.5 Cube compression failure form of specimens

2.3 三点弯曲性能

试件的荷载-挠度（P-δ）曲线如图6所示.为保证图幅整洁，每组只分析1条抗折强度最接近平均值的曲线.由图6可见：在加载初期，试件的荷载随挠度基本呈线性变化，钢纤维的掺入使其与基体成为一个整体共同承担拉应力，二者变形协调处于弹性阶段；在达到峰值荷载之后，无纤维地质聚合物迅速丧失承载力，P-δ曲线迅速下降，呈现明显的脆性破坏；掺入钢纤维后，由于钢纤维的增强、增韧效果，P-δ曲线下降段变得饱满，表现出良好的韧性，呈延性破坏；相较于杂向钢纤维，定向钢纤维的掺入使复合梁承载力得到较大提升，曲线愈发饱满，裂缝扩展缓慢，延性增加.

图6 试件的荷载-挠度曲线Fig.6 Load-deflection curves of specimens

由图6还可见，除R00组外，各组试件曲线下降段均伴随有锯齿形波动现象，且随着定向钢纤维层厚度的增加而变得更加明显持久.这是由于钢纤维发挥了桥连作用，在受弯破坏过程中，钢纤维主要存在脱黏、拔出、滑移3个阶段，当纤维轴向力增大至纤维埋入段与基体之间极限黏结承载力时，纤维脱黏并出现滑拔，从而使荷载出现突降；随着荷载增大，裂缝不断向上发展，新裂缝间定向纤维的出现阻碍了裂缝的持续扩展，荷载突降过程终止，桥连纤维停止滑拔，此时纤维抗滑拔能力由纤维与基体间的静摩擦主导，纤维的受荷能力增加，从而引起荷载上升.随着钢纤维层厚度的增加，起到上述桥连作用的钢纤维数量增多，当裂纹连续张开时，桥连纤维在不断裂的情况下继续承受并传递应力，锯齿形波动也就频繁出现，由此可见，定向钢纤维可有效抑制裂纹形成，控制断裂过程，提供有效的开裂强度.

断裂能（GF，N/mm）是形成单位面积裂缝所需要的能量.对于脆性材料，其断裂能可由式（1）给出；对于纤维增强韧性材料，其断裂面除了基体的主断裂面外，还有纤维与基体间的黏结破裂面.目前尚无相对成熟的计算公式，本文仍采用式（1）进行复合梁断裂能的计算.

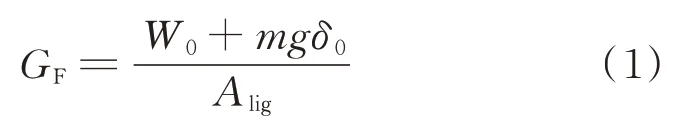
式中：W0为外荷载做的功，通过计算试件P-δ曲线下的面积得到，N·mm；m为试件的质量，kg；g为重力加速度，N/kg；δ0为试件最终破坏时的挠度，mm，本文将荷载降至峰值荷载的10%时视为试件最终破坏；Alig为试件的断裂韧带面积，mm2.

基于式（1）计算得到试件的断裂能，结果如图7所示.由图7可见：各试件的断裂能随着定向钢纤维层厚度的增加而增加；D100组断裂能较R00组和R100组分别提高了55倍、3倍.由于无纤维增强地质聚合物呈现明显的脆性破坏，在达到峰值荷载后试件迅速破坏，消耗的能量也就相对较小；而钢纤维的掺入使地质聚合物脆性破坏转为延性破坏，在达到峰值荷载后，由于钢纤维的桥接作用，复合梁不会立即破坏，此时承载力缓慢下降，裂缝缓慢扩展的过程中伴随着钢纤维的滑拔，断裂能随之大幅提高.钢纤维在此过程中存在着摩擦阻力和变形抗力，滑拔所消耗的能量远远大于基体开裂消耗的能量，由此可见，在复合梁断裂过程中，对能量消耗起主导作用的是裂缝处钢纤维的滑拔.钢纤维在拉应力上的定向分布使其横跨裂缝，上述作用效果愈发明显，纤维得到充分滑拔，所产生的断裂能也就随之增长.

图7 试件断裂能随钢纤维层厚度变化曲线Fig.7 Fracture energy curve with steel fiber layer thickness of specimens

由图7还可见：随着定向钢纤维层厚度的增加，试件的断裂能总体上呈上升趋势，但增速呈现先快后慢的变化趋势，当钢纤维层厚度不大于45 mm（即梁高的0.45）时，试件的断裂能增速较快，当钢纤维层厚度大于45 mm时，试件断裂能的增速减缓.这是由于当钢纤维层厚度较小时，裂缝快速贯通穿过钢纤维层，且随着荷载的增加，梁下部裂缝宽度越来越大，虽然钢纤维层厚度较小，但有充分的时间和空间用以滑拔，滑拔位移不断增大，断裂能随之快速增长；当钢纤维层厚度较大时，虽然下部处于裂缝宽度较大的钢纤维能够充分发挥作用，但上部处于裂缝宽度较小的钢纤维滑拔消耗的能量十分有限，导致断裂能增速减缓.

各组试件的峰值荷载和抗折强度平均值如表3所示.由表3可见：复合梁的抗折强度随着定向钢纤维层厚度的增加呈现先增后减的变化趋势，当钢纤维层厚度为60 mm（梁高的0.6）时抗折强度达到最大值；相较于无纤维地质聚合物，全截面杂向和定向钢纤维增强地质聚合物的抗折强度分别提高了64%和257%.

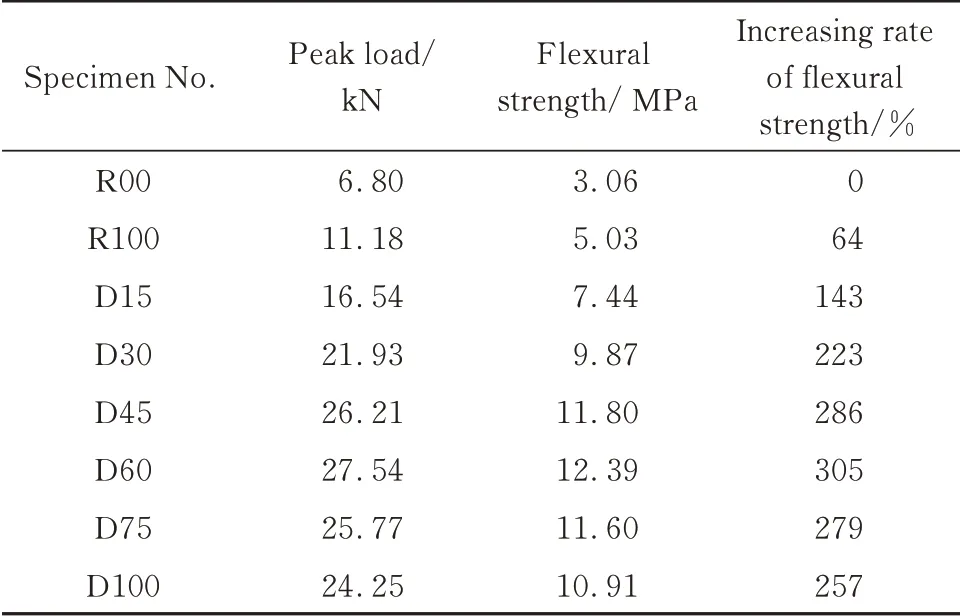
表3 各组试件的峰值荷载和抗折强度Table 3 Peak load and flexur al str ength of each specimen

在弯曲破坏过程中，裂缝自下而上缓慢发展，拉应力由裂缝处的钢纤维与未开裂的基体共同承担，钢纤维的存在不仅降低了应力集中，而且可以桥连微观裂缝，转移荷载，延缓裂缝的发展，从而提高其抗折强度.当钢纤维定向分布后，钢纤维方向与拉应力方向一致，钢纤维的增强、增韧效果得到提高，抗折强度随之增加.

当定向钢纤维层厚度较小时，钢纤维始终存在于受拉区中，开裂后裂缝很快扩展贯通纤维层，钢纤维起到的增强、增韧效果十分有限；当钢纤维层厚度较大时，虽然受拉区钢纤维充分发挥增强作用，但受压区也存在钢纤维，且该钢纤维的方向与压应力方向一致，钢纤维存在于受压区并不能发挥其优异的抗拉作用，反而可能影响受压区基体孔隙和密实度，导致内部薄弱区不断增大，抗折强度不增反减.

2.4 讨论

为更好地描述定向钢纤维层厚度与地质聚合物正截面抗弯承载力之间的关系，对比分析部分和全截面钢纤维增强地质聚合物的正截面承载力.本文将部分和全截面钢纤维增强计算模型中受压区应力分布均简化为等效矩形应力，其强度值分别为无纤维和钢纤维增强地质聚合物的轴心抗压强度，分别用fcm和fcm1表示.不考虑基体承担的拉力，将受拉区应力分布也简化为矩形，其强度值为钢纤维增强地质聚合物抗拉强度，用fftb表示.

图8为部分钢纤维增强地质聚合物受弯承载力计算模型.其中b和h分别为梁的宽度和高度，εs和εc分别为受拉区、受压区应变，x0为受压区高度，x为等效受压区高度，Mfu为正截面受弯承载力.

图8 部分钢纤维增强地质聚合物受弯承载力计算模型Fig.8 Calculation model of flexural capacity of partially steel fiber reinforced geopolymer

由图8可列出以下基本方程：

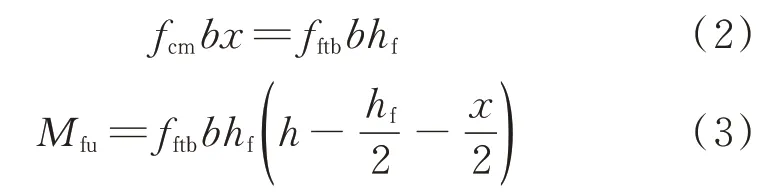
由式（2）可得：

将式（4）代入式（3），可得：

式（5）给出了部分钢纤维增强地质聚合物正截面受弯承载力与钢纤维层厚度的关系，对式（5）中的hf求导，并令＝0，可得：

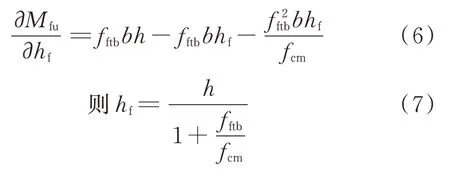
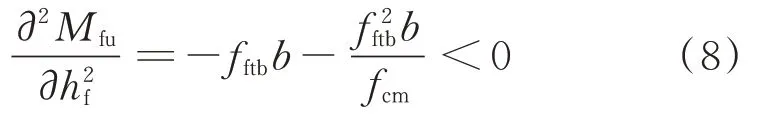
由 式（8）可 知，式（5）为 凸 函 数，即 当hf＝时，Mfu存在极大值.

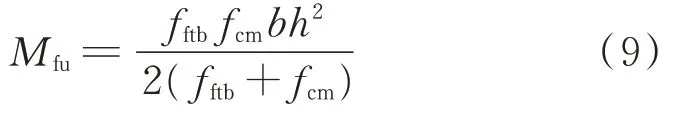
上述推导表明：存在1个界限钢纤维层厚度，使得部分钢纤维增强地质聚合物的正截面受弯承载力达到极大值.对式（7）进一步分析可知，该界限钢纤维层厚度与钢纤维增强地质聚合物抗拉强度和地质聚合物基体抗压强度的比值有关，表明该界限钢纤维层厚度并非一个定值.

图9为全截面钢纤维增强地质聚合物受弯承载力计算模型.其中，εs1和εc1分别为受拉区、受压区应变；x01为实际受压区高度；x1为等效受压区高度，其值取实际受压区高度的0.8；xt1为受拉区高度，Mfu1为正截面受弯承载力.

由图9可列出以下基本方程：

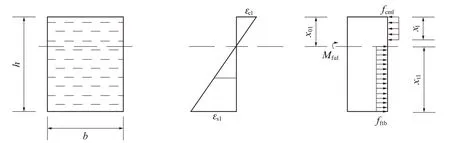
图9 全截面钢纤维增强地质聚合物受弯承载力计算模型Fig.9 Calculation model of flexural capacity of full section steel fiber reinforced geopolymer

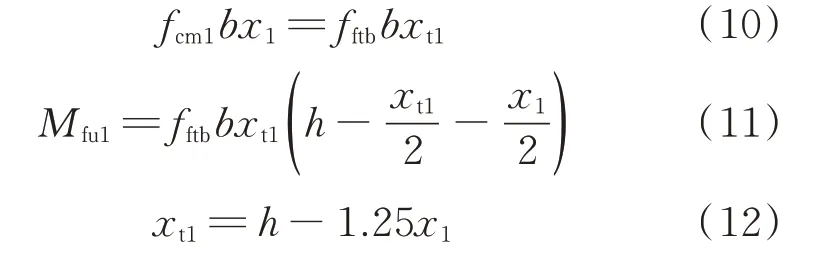
将式（12）代入式（10），可得：

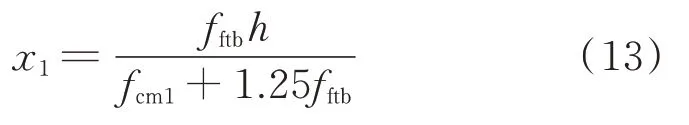
再将式（12）、（13）代入式（11），可得：

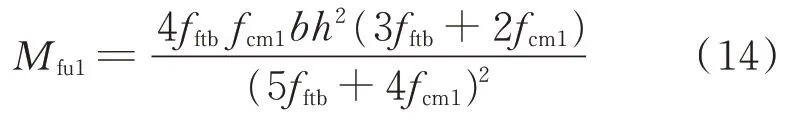
为进一步判定部分钢纤维增强地质聚合物的正截面受弯承载力的极大值是否为全截面纤维厚度范围内的最大值，将式（14）与式（9）进行作差对比，见式（15）.

结合表2可知，与压应力方向平行的钢纤维增强地质聚合物抗压强度小于无纤维增强地质聚合物抗压强度，即fcm1＜fcm.同时对式（15）进行分析可知，当fcm1-fcm＜0时，Mfu1-Mfu＜0，说明全截面钢纤维增强地质聚合物的受弯承载力小于部分钢纤维增强地质聚合物的最大受弯承载力，与试验结果吻合.

为了进一步分析理论模型的合理性，对钢纤维增强地质聚合物承载力计算值与试验值进行量化对比分析.由式（5）、（14）可知，fcm和fftb值是计算钢纤维增强地质聚合物承载力的关键.鉴于目前对于地质聚合物材料尚未有成熟的公式可以借鉴，参考GB 50010—2010《混凝土结构设计规范》和CECS 38：2004《钢纤维混凝土结构设计与施工规程》，fcm和fftb按式（16）、（17）进行计算：

式中：αc1为混凝土轴心抗压强度平均值与立方体抗压强度平均值的比值，C50及以下混凝土取为0.76；αc2为混凝土的折减系数，C40及以下混凝土取为1.0；fcu为混凝土立方体抗压强度.

式中：βtu为钢纤维抗拉强度影响系数，可通过试验确定，当钢纤维混凝土的强度等级为C20～C40时，βtu＝1.3；λf为钢纤维掺量特征值（ρf为钢纤维体积分数，lf为钢纤维长度，df为钢纤维直径）；ft为混凝土抗拉强度（ft＝0.395f0.55cu）.

需要说明的是，式（17）中βtu的参考取值是基于传统杂向钢纤维试验结果的，对于定向超细镀铜钢纤维增强地质聚合物材料，该系数的取值还有待深入研究.故本文以βtu为参数，探讨钢纤维增强地质聚合物材料受弯承载力随βtu的变化规律，其计算结果如图10所示.

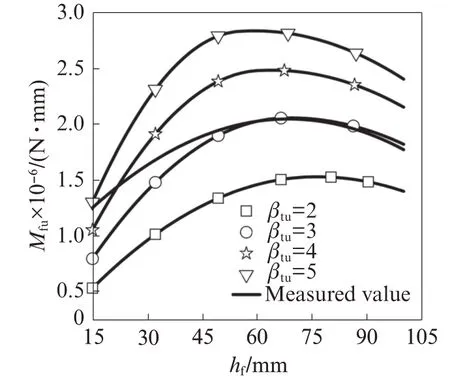
图10 不同βtu下钢纤维增强地质聚合物材料受弯承载力随钢纤维层厚度变化曲线Fig.10 Bending curves of steel fiber reinforced geopolymer with steel fiber layer thickness under differentβtu

由图10可见：当βtu一定时，钢纤维增强地质聚合物材料受弯承载力随钢纤维层厚度的增加呈现先增后减的变化趋势；随着βtu的增大，曲线逐渐上移；当βtu达到3时，钢纤维增强地质聚合物材料的承载力与试验结果较为吻合，随着钢纤维层厚度的增加，二者的偏差逐渐减小，在钢纤维层厚度达到梁高的0.45（45 mm）之后，曲线几乎重合.

对不同βtu下承载力最大值对应的钢纤维层厚度进行统计，发现当βtu≈3，界限钢纤维层厚度为梁高的0.68左右时，与试验结果0.6较为吻合.

3 结论

（1）定向钢纤维增强地质聚合物在抗压强度上表现出各向异性，当定向钢纤维方向与加载方向垂直时，抗压强度提高13%；当定向钢纤维方向与加载方向一致时，抗压强度降低27%.

（2）定向钢纤维的掺入显著提高了地质聚合物的断裂能，较空白试件最多提高55倍，且断裂能增速随着钢纤维层厚度的增加呈现先快后慢的变化趋势.

（3）复合梁的抗折强度随着钢纤维层厚度的增加呈现先增加后降低的趋势，与空白组相比，钢纤维层厚度为梁高的0.6时抗折强度达到最大值，从3.06 MPa增加到12.39 MPa.

（4）界限钢纤维层厚度并非定值，它与定向钢纤维增强地质聚合物抗拉强度及无纤维增强地质聚合物抗压强度有关.结合定向钢纤维增强地质聚合物抗压强度的各向异性测试结果，所建立的简化模型较好地诠释了部分定向钢纤维增强地质聚合物抗折强度随钢纤维层厚度的变化趋势.以定向钢纤维抗拉强度影响系数（βtu）为参数，计算并对比分析了部分定向钢纤维增强地质聚合物受弯承载力与界限钢纤维层厚度，表明当βtu≈3时，计算结果与试验结果较为吻合.