重力坝抗滑稳定可靠度动态评估模型研究与应用

甘珩佚，陈建康，高 山，吴震宇，周靖人

（1.四川大学水力学与山区河流开发保护国家重点实验室水利水电学院，成都 610065；2.四川省水利水电勘测设计研究院有限公司，成都 610072）

0 引 言

混凝土重力坝因其施工工艺简单，耐久性和抗渗性好等优点，在水利工程中得到广泛应用［1］，如位于广西的龙滩重力坝和位于四川的官地重力坝等［2］。据统计，重力坝失事事故中，因地基破坏导致失稳的比例高达40%［3］。受复杂运行环境和材料劣化等因素的影响，重力坝抗滑稳定安全具有时变特征，结合实时反映大坝安全性态的安全监测数据，实现监测-模拟数据的同化与融合，建立重力坝抗滑稳定安全风险-监测数据耦联模型，实时跟踪大坝抗滑稳定性态的动态演变，实现大坝稳定安全风险实时评估与预警，具有重要的理论意义与应用价值［4］。

重力坝抗滑稳定及其实时评估预测问题是近来的关注焦点［5］。杨志勇等改进了重力坝设计规范中的坝基抗滑稳定计算，以双滑面深层抗滑稳定导出简化的分项系数多滑面公式，取得了较好的预测效果［6］；彭圣军利用优化算法融合混沌理论对大坝位移进行拟合和预测，构建了考虑残差馄饨因子的混凝土坝位移混合监控模型，实时监控和预测大坝的安全性［7］；谷艳昌等以大坝溃决模式与坝体结构特性转异为纽带，利用有限元计算获得相应的变形临界值，进而建立了基于风险管理的大坝变形预警指标［8］。沈振中［9］等将基于块体理论的非连续变形分析引入重力坝安全因素和预警指标研究中，根据失稳判据和坝体位移与强度折减系数之间的关系曲线确定了大坝的结构性态，并估计出大坝弹性状态和承载极限状态的变形预警指标。但结合实时监测数据的抗滑稳定安全评估方法鲜见报道，因此，如何利用监测数据实时对大坝安全进行评估，尽早对潜在的危险进行预警，将灾害风险和损失降为最低是我们急需解决的问题。

本文结合坝基岩体蠕变与瞬时变形参数反分析技术，构建了重力坝抗滑稳定响应面功能函数，提出了基于大坝变形监测数据的重力坝抗滑稳定可靠度动态评估模型，并将其应用到GD重力坝抗滑稳定安全分析与预测中，验证其有效性和适用性。

1 重力坝材料参数反分析方法

1.1 基于统计回归模型的重力坝变形时效位移分量提取

在重力坝的变形统计回归预测模型中，其因子函数主要由时效分量、温度分量与水压分量构成。因此，其统计回归模型表达式如式（1）所示。

式中：Y(t)为坝体变形监测值在时间t的统计估计值；F1[θ(t)]为坝体变形的时效分量；F2[θ(t)]为坝体变形的温度分量；F3[H(t)]为坝体变形的水压分量。

时效分量是随时间推移而朝某一方向发展的不可逆的分量，一般采用指数式、对数式、双曲线式等表示，本文采用的时效因子函数为对数线性式［10］，即：

式中：ti为观测的总天数；c1、c2为待回归系数。

温度对重力坝位移的影响主要表现在气温的季节性变化上，本文采用的温度因子函数为多段平均气温的线性组合［11］。

式中：Ti为观测日当天、前3 d、前5 d、前10 d、前15 d、前30 d 的平均大气气温。

水压分量一般与重力坝变形的转角、扭矩等有关，本文采用的水压分量函数为：

式中：H(t)为变形观测日的平均水位；H(t0)为基准水位；Hi(t)为观测日当天、前1～3 d、前4～7 d、前8～15 d、前16～30 d、前31～60 d平均水位；ai为待回归系数［12］。

综上所述，经过上述对各因子函数的选取，建立重力坝变形监测分析数学模型为：

基于上述模型，重力坝变形的时效位移分量可表达为：

1.2 基于时效位移的坝与地基材料参数反分析

按最小二乘法可构建参数反分析的目标函数，如式（7）所示：

式中：E为反分析目标函数值；x为待求参数，其上下限由统计资料得到；δ*i为测点i的实测位移；δi(x)为测点i的响应面函数输出位移；k为测点总数［13］。

在混凝土坝-地基系统瞬时-蠕变参数反分析过程中，在不同时刻每个监测点都有不同的监测值，因此需要构建响应面方程序列来拟合坝体在时间过程中的变形特征，目标函数可以表示为：

式中：F为目标函数；δ*i(tj)为监测点i在不同时刻下的实测位移；δi(x1，x2，…，xn，tj)为监测点i的响应面函数输出位移历时过程；x1，x2，…，xn为E-B 模型和蠕变模型中待反演的参数；k为选取的目标监测点数量；m为选取的时间节点总数［14］。

结合式（8）所示目标函数，将遗传算法运用在混凝土坝-地基系统瞬时-蠕变参数反分析中，通过参数编码、基因重组和适应性选择推动族群进化从而得到最优参数。本文模拟蠕变采用的本构模型为Burgers蠕变本构，模拟瞬时变形采用DP本构模型。

影响混凝土重力坝变形的材料参数众多，传统的位移反分析采用对所有参数进行反分析，导致计算效率低，且参数之间的相互影响可能导致次要影响因素遮蔽主要影响因素。为此，本文针对影响大坝变形的岩体材料物理力学参数采用极差分析法和方差分析法确定影响大坝变形的关键参数。本文基于岩石蠕变特性与监测时效变形的物理意义，利用大坝位移统计回归模型分离出的时效分量，建立基于时效变形的重力坝参数反分析方程，其具体步骤如下：

（1）根据敏感性分析的结果择取对大坝变形有高度影响的参数作为反演目标参数；

（2）建立大坝位移监测点位移的统计方程，分离出监测点位移的时效分量，作为反分析的目标值；

（3）根据设计资料中的材料设计参数来确定反演参数的合理取值范围。

（4）采用正交试验法进行试验设计，通过参数分布类型抽样或根据建议取值范围确定试验中参数水平。

（5）进行每组试验的分析计算，统计整理每个监测点的数值模拟结果。

（6）构建每个序列典型时刻位移差响应面方程，求解响应面方程的系数。

（7）以监测点位移的时效为目标值，构建反分析的目标函数，采用遗传算法对目标函数进行求解，得到反分析参数的最优解。

（8）利用反分析得到的影响大坝变形关键参数的优化解，进行大坝变形分析，比较模拟值与实测值的误差，若误差精度满足要求，则可终止反分析循环，得到的参数即为目标优化解；若精度不满足要求，重复步骤（3）～（7），至精度满足要求为止。

2 基于监测数据的重力坝抗滑稳定可靠度预测模型构建

2.1 抗滑稳定功能函数构建

对重力坝与地基结构体系而言，设其随机变量为x1、x2、…、xn，定义功能函数G=g(x1，x2，…，xn)来表征结构与地基的工作状态，则其极限状态可以表述为

在重力坝抗滑稳定分析中，建基面或者深层滑动面动力大于阻滑力均属超承载能力极限状态。在有限元分析中重力坝抗滑稳定可用抗剪断公式表达，因此重力坝抗滑失稳功能函数可构建为：

式中：f′i、ci为滑裂面第i个单元的抗剪强度指标；σi为第i个单元滑裂面方向受到的正应力；τi为第i个单元滑裂面方向受到的切应力；li为第i个单元沿滑裂面方向的单元长度；n为整个滑裂面上所有单元的总数［15］。

基于式（10），采用蒙特卡洛法计算抗滑稳定可靠度，即随机抽取随机变量X的样本值{x1，x2，…，xn}T，以功能函数值G(X1，X2，…，Xn)≤0 的次数占总抽样次数比获得失效风险Pf。为便于分析，此处可以构造一个取值为0和1的函数，即：

式中：Df表征结构的失效域，即G(x)∈Df时，结构失效；反之，结构可靠。

因此，坝与地基失效风险可以表达为：

式中：为坝与地基失效风险的抽样估计值；N为总抽样数；G(x)i为第i次抽样对应的功能函数值。

综上，重力坝与地基抗滑稳定安全的可靠指标为

2.2 基于监测数据的抗滑稳定可靠度预测模型构建

大坝安全状态最直观的反映就是监测数据，测点测值的大小、变化趋势等与大坝稳定安全状态密切相关。以重力坝的安全监测数据为基础，结合数值模拟成果，以测点变形监测序列为自变量，重力坝抗滑稳定可靠度为因变量，构建重力坝的稳定可靠度评估模型：

式中：F[Y(t)]为测点变形分量；βs(t)为重力抗滑稳定可靠指标在时间t的统计估计值；C为待定常数项。

式中：ai为待定系数；yi为变形序列的监测值；n为变形序列的个数。

实际工程中，大坝变形测点测值一般包括四部分，即水压分量、时效分量、环境量影响及系统误差等，因此：

式中：F1[H(t)]为监测点水压分量；F2[T(t)]为温度分量；F3[θ(t)]为时效分量；C为待定常数项。

因本次有限元计算中未考虑温度因素，仅利用时效和水压分量构建可靠度预测模型，故将上述方程中变形值的时效和水压分量分离出来构建大坝抗滑稳定可靠度预测模型。

式中各分量定义同上。

本文提出的基于监测数据的抗滑稳定可靠度预测模型构建流程如图1所示。

3 工程应用

3.1 工程概况

GD 重力坝位于四川省凉山彝族自治州西昌市和盐源县交界的打罗村境内。主体枢纽主要由拦河碾压混凝土重力坝、泄洪消能建筑物、引水发电建筑物等组成，工程为一等大（1）型工程，坝轴线方向N12°E，拦河坝坝顶高程1 334 m，坝顶长度516 m。水库正常蓄水位1 330.00 m，设计洪水位1 330.18 m，校核洪水位1 330.44 m，死水位1 328.00 m，极限死水位1 321.00 m，总库容7.6 亿m3，属日调节水库。电站装机容量2 400 MW，多年平均发电量118.7 亿kWh。

本次反演分析选用GD 重力坝的9#坝段，该坝段为一挡水坝段，建基面高程1 186 m，坝顶高程1 334 m，最大坝高148 m，工程地质条件较复杂。倒垂测点IP3 和双金属标测点DS3 埋设在1 205 m 的大坝下部，最低端位于1 155 m，与基岩紧密结合；真空激光测点LA9、LA1分别布置于高程1 334 m 的坝顶和高程1 205 m的大坝底部廊道内。GD水电站相关监测仪器布置图如图2所示。

3.2 有限元模型

有限元模型的模拟范围为：自建基面向下延伸2.5 倍坝高（约370 m），上下游方向同样延伸2.5 倍坝高（约370 m）。为对比计算位移与实测位移，根据真空激光测点LA9、倒垂线测点IP3、双金属标DS3的埋设位置，在有限元模型中布料，其中坝体由C15、C20、C25 三种标号的碾压混凝土和C20 标号的常态混凝土组成，坝基由Ⅱ类、Ⅲ类、Ⅳ类、Ⅴ类岩体、断层和破碎带组成。有限元模型共划分为65 190 个单元和73 964 个结点。大坝三维模型顺河向X轴以指向下游为正，铅直向Y轴以垂直向上为正，横河向Z轴以指向右岸为正，模型及材料分区如图3所示。

3.3 重力坝坝基岩体参数反分析

3.3.1 参数敏感性分析

本文模拟蠕变采用的本构模型为Burgers蠕变本构，该模型主要有Maxwell 剪切模量mshear、Kelvin 剪切模量kshear、Maxwell 黏滞系数mviscosity、Kelvin 黏滞系数kviscosity 四个参数，模拟瞬时变形采用DP 本构模型，该模型主要有E弹模，c凝聚力，φ摩擦角3个参数。而GD重力坝9号坝段共4类岩体8个蠕变参数，15个力学参数。根据GD重力坝监测点的布置情况，选取9号坝段的坝顶激光位移测点LA9以及底部廊道中的激光测点LA1 作为此次分析的特征点（如图4）。通过数值模拟，采用极差分析法和方差分析法分别对特征点的顺河向位移、垂直位移和综合位移三个目标量进行敏感性分析。

极差分析法和方差分析法显示，坝体C25 碾压混凝土的E；C20 碾压混凝土的E、c；II 类岩体的E、c、φ、mshear、kshear、mviscosity、kviscosity；Ⅲ类岩体的E、c对大坝变形均有影响或有显著影响。因此，选择以上参数作为此次反分析参数。

3.3.2 坝体与地基参数反分析

选取9 号挡水坝段的坝顶激光位移测点LA9、底部廊道中的倒垂测点IP3 和双金属标测点DS3 作为参数反演分析的特征点，选取目标序列2014.8.1、2015.8.1、2016.8.1 和2017.8.1 的测值为目标值进行参数反分析，蠕变参数与DP 模型参数反演结果见表1。

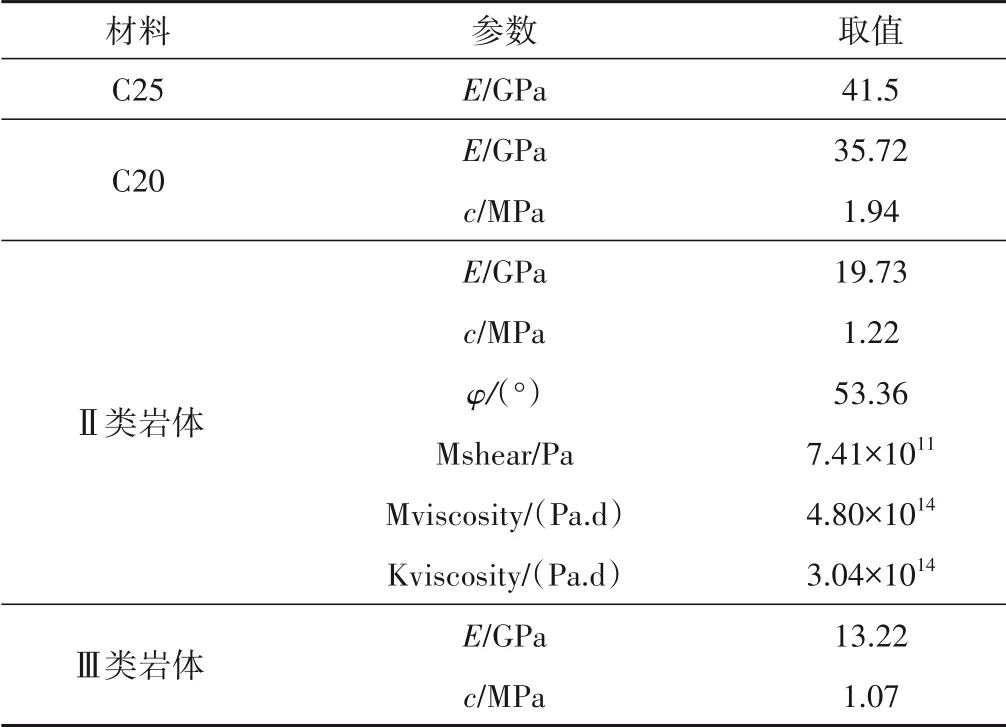
表1 反演参数表Tab.1 Inversion parameter table

对所有序列进行误差对比分析，其反分析参数模拟值与实测值最大误差均在19%以内；选择时间序列的中间节点2016.12.31 和末尾端点2018.12.31 作为误差分析的结果展示，根据表1中大坝变形参数的优化解和初始设计值，分别对GD重力坝的变形进行数值模拟分析，如表2所示，通过有限元模拟与测值比较分析可见，采用设计参数的变形模拟值与实测值的最大误差50.21%，平均误差为25.49%。采用反分析参数模拟值与实测值的最大误差17.43%，平均误差10.56%，误差在合理范围内，曲线吻合较好，表明参数反分析效果良好，可以反映大坝的变形性态。

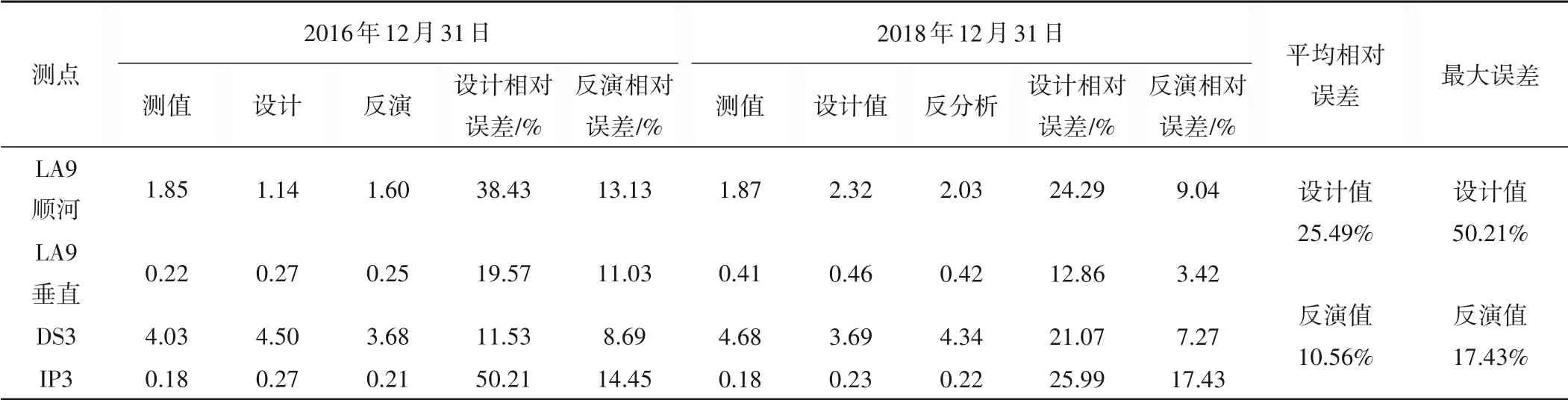
表2 参数反演误差统计表Tab.2 Statistical table of parameter inversion error

3.4 抗滑稳定可靠度预测模型构建

3.4.1 失效通道搜寻

本文采用荷载增量法搜索最危险的滑移通道。GD 重力坝坝基滑移通道如图5所示。

3.4.2 抗滑稳定可靠度分析

本文确定材料的特征值如表5，坝基岩体的弹模E、凝聚力c和内摩擦角φ以及坝体C25 混凝土、C20 混凝土的弹模E考虑为随机变量。

表3 材料参数随机特征Tab.3 Random characteristics of material parameters

采用不含交叉项的二次多项式，构建GD 重力坝抗滑稳定安全系数响应面方程。采用正交试验法，获得不同时刻大坝抗滑稳定响应面方程系数。本次分析的时间序列为2012.4.1-2018.12.31，在该时间段内每隔3 个月建立一个响应面方程，共计建立28 个响应面方程来评估其运行期可靠度，本次28 个响应面方程拟合效果较好，复相关系数均大于0.88，响应面方程具有良好的显著性。

进行大坝抗滑稳定可靠度分析时需要对参数进行截尾处理，参数在均值的3σ范围内取值有99.7%的保证率，故选择μ-3σ、μ+ 3σ分别为随机变量的左右截尾点，根据关键滑移通道响应面方程，采用蒙特卡洛法获得大坝抗滑稳定的可靠指标β与失效概率Pf历时曲线见图6。由图6可见，大坝初期蓄水阶段可靠指标相对较低，2014年后水位仅在小范围内波动，可靠指标也在小范围内呈现相似的波动趋势。现阶段可靠指标达到4.27，其变化趋于稳定。

3.4.3 抗滑稳定可靠度预测模型构建

基于本文提出的重力坝抗滑稳定可靠度动态评估模型和式（13），集合2012.4.1-2018.12.31 间的可靠度模拟值，构建GD重力坝可靠度预测模型，如图7所示。结果显示，复相关系数大于0.93，可靠指标计算与拟合值平均误差0.79%，最大误差1.55%，精度较高，预测模型如式（14）所示。通过对后180 d 和360 d 大坝抗滑稳定可靠指标预测分析，其平均误差和最大误差如表6所示都在5%以内。工程应用表明，本文提出的基于监测数据的重力坝抗滑稳定可靠度动态评估模型效率和精度较高，工程应用价值明显。

式中：y1为IP3 顺河向位移时效分量；y2为DS3 垂直位移时效分量；y3为LA9 顺河向位移时效分量；y4为LA9 垂直位移时效分量；y5为LA9 顺河向位移水压分量；y6为LA9 垂直位移水压分量；y7为DS3 垂直位移水压分量；y8为IP3 顺河向位移水压分量。

表4 大坝抗滑稳定可靠指标预测精度统计Tab.4 Prediction accuracy statistics of reliability index of dam anti-sliding stability

4 结 论

本文通过对重力坝与地基材料参数反分析，抗滑稳定可靠度及其动态预测模型的深入研究，获得以下几点认识：

（1）针对坝与地基材料参数众多，参数设计值难以准确表征材料性能等问题，采用极差分析和方差分析法，提取影响重力坝变形的关键影响参数，通过时效位移分离、目标函数构建和参数优化求解，提出了基于时效位移的混凝土与岩体参数反分析方法。

（2）采用荷载增量法确定重力坝抗滑稳定危险滑面，基于蒙特卡洛抽样模拟，通过抗滑稳定安全时变可靠度分析，构建了抗滑稳定可靠度-监测数据耦联预测模型，提出了重力坝抗滑稳定实时评估方法。

（3）GD工程应用表明，基于反演参数得到的位移模拟结果与监测数据平均误差小于11%，表明本文提出的方法精度较高。提出的抗滑稳定可靠度预测模型平均误差为0.79%，最大误差为1.55%，精度高，适用性好。□