VIC模型系统微分响应参数率定方法在大坡岭流域的应用
2021-12-30孙苗苗瞿思敏陈学秋包沐曦宋兰兰
孙苗苗,石 朋,瞿思敏,陈学秋,徐 瑶,游 洋,包沐曦,宋兰兰
(1.河海大学水文水资源学院,南京 210098;2.水利部珠江水利委员会水文局,广州 510611;3.江苏省水利科教中心,南京 210003;4.江苏省水利厅,南京 210029;5.南京海事局,南京 210009)
0 引 言
流域水文模型是研究降雨径流形成机理及时空变化规律的有效工具[1]。分布式水文模型能考虑流域特征空间变异性且具有物理基础,在水文模拟中具有优越性,是当前流域水文模拟的重要发展趋势之一[2]。在众多分布式水文模型中,VIC(Variable Infiltration Capacity)模型因其操作原理简单、模拟精度较好的特点,被广泛成功应用于国内外不同尺度的流域,研究区域覆盖广,研究内容涉及丰富,包括径流模拟、模型改进及气候和土地覆被变化对水资源影响等诸多方面[3-9]。
水文模型的模拟效果很大程度上依赖于模型参数的选择,因此,选择合理、高效的参数率定方法极其重要[10]。目前,大多数的参数率定方法采用误差平方和目标函数来进行评估,但误差平方和的累加过程损失了有效信息,其提供的信息存在诸多不合理甚至是错误的。近年来,河海大学的包为民教授提出了系统微分响应参数率定方法[11,12],该方法能有效避免现有参数率定方法的绝大多数问题,并在新安江模型、SAC 模型等的参数优化中均取得了较好的应用效果[10,13],但该方法在大尺度分布式水文模型上的应用研究相对较少。基于上述原因,本文选取淮河上游大坡岭子流域为例,在对模型参数敏感性分析的基础上,将系统微分响应参数率定方法与VIC模型相结合,探究验证其在大尺度分布式水文模型中的适用性。
1 研究方法
1.1 VIC模型
VIC 模型[14]基于SVATS(Soil Vegetation Atmospheric Transfer Schemes)思想的空间分布网格化的大尺度分布式水文模型。模型主要通过考虑大气、植被、土壤之间的物理化学生物等转化过程来反映陆面各部分间的水热状态变化和传输状况,可同时模拟水循环过程的水量平衡和能量平衡,在实际应用中,也可只计算水量平衡[15]。
VIC 模型规定对研究区域网格化,在每个网格内分别考虑了裸地及多种植被覆盖类型。在蒸散发过程中,同时考虑了植被冠层蒸发、植被蒸腾及裸土蒸发。在产流计算方面,VIC-3L模型将土壤划分为三层,顶薄层和上层土壤产生直接径流,下层土壤产生基流[15],其中,直接径流的计算考虑了蓄满产流和超渗产流两种机制,基流则根据Arno 概念模型[16]计算。VIC 模型无汇流模型,本文采用了Dag Lohmann 等人开发的汇流模型与之耦合。
1.2 系统微分响应参数率定方法
系统微分响应参数率定方法(System Response Parameter Calibration Method,SRPCM)是一种基于参数函数曲面的参数估计寻优方法[17,18]。不同于传统优化在目标函数曲面寻找参数优值的想法,该方法在参数函数曲面上寻优,成功解决了目标函数带来的问题[10]。
水文模型常可看作为没有明确表达式的函数Yt=f(P,Xt),其中,模型的输入是自变量Xt,模型的输出为因变量Yt,模型参数为函数参数P,当Xt确定不变后,Yt随P而改变,这便形成了定义在参数空间域上的函数曲面。
给定一个实测样本(Xt,Qt),将自变量代入函数或模型可得:
式中:Xt取实测值;Yt随参数P而改变,把该式定义的函数称为参数函数。
将实测样本(Xt,Qt)代入函数或模型得:
上式是与特定实测样本对应的参数域函数,将式(2)定义的函数称为样本函数。
利用系统微分理论,对于一个多参数函数Yt=f(Pi,Xt),对自变量{P1,P2,…,Pn}进行微分可得:
式中:函数增量dYt随参数增量{dP1,dP2,…,dPn}而改变,称为参数增量的全微分系统响应。当只改变某一参数Pi其他参数不变时,函数增量dYt是参数增量dPi的偏微分系统响应。
因水文模型常常没有明确数学表达式,无法进行偏微分的计算,因此可用差分格式。对式(3)中向前差分可得:
式中:Pji表示参数Pi的第j次率定;Pji+1=Pi+ ΔPi表示参数Pi的第j+ 1 次率定;其中ΔPi为参数Pi增加的一个微小值。将f ij表示为代入Pji的函数值,f ij+1表示为代入Pji+1的函数值,则式(4)可表示为:
则考虑所有参数的差分表达式为:
假设有N组实测样本(X1,Q1),(X2,Q2),…,(XN,QN),将其代入式(6),可得:
用向量形式表示式(7)如下:
式中:e为实测值Q与函数计算值f j+1的偏差;s是参数灵敏度矩阵,表达式如下:
对新的估计参数Pj+1应使式(8)的误差平方和(SLS)最小,即minPϵRn{SLSj+1=(Q-f j+1)T(Q-f j+1)}。
当minPϵRnSLSj+1= 0时,结合式(8)可得Pj+1的最佳估计:
系统微分响应参数率定方法的具体计算步骤如下:
(1)设置参数初值P0,输入N组实测值(X1,Q1),(X2,Q2),…,(XN,QN),令j= 0,Pj=P0;
(2)将模型输入X1,X2,…,XN和参数Pj代入模型计算得到一组输出f j=(f1,f2,…,fN),并根据式(9)计算参数灵敏度矩阵s;
(3)根据式(10)确定新参数Pj+1;
(4)判断参数及模拟结果是否满足收敛条件,若是则退出寻优,否则令j=j+ 1,跳转到第(2)步继续循环。
2 区域概况及数据
2.1 研究区域概况
淮河流域位于我国东部,介于黄河、长江两流域之间,流域经纬度范围分别为:111°55′~121°25′E,30°55′~36°36′N。本文选取的研究区域是位于淮河干流上游的大坡岭水文站以上流域(图1),该站控制流域面积为1 640 km2,干流长度为73 km。大坡岭流域属暖温带半湿润季风气候,气候温和,流域多年平均降雨量为918 mm。流域内地形以山区和丘陵区为主,水利工程不多。流域地处亚热带常绿阔叶林带,植被资源丰富,主要的土地利用类型为农林业,主要作物为水稻[19]。
2.2 研究区数据
构建VIC模型需要的输入数据主要分为以下4类:
(1)地形数据。采用了SRTMDEM(90M)分辨率原始高程数据,使用ARCGIS 将研究区划分成61 个0.05°×0.05°分辨率的网格单元并生成水系等,见图2(a)。
(2)气象强迫数据。来自中国地面气候资料日值数据集(V3.0),选取了大坡岭流域及临近气象站2007年1月1日-2014年12月31日的气象资料,采用IDW 法插值获取降雨量、日最高气温、日最低气温及风速四个气象要素在流域内的分布。
(3)植被数据。植被分类采用的是马里兰大学(UMD)发布的全球1 km 分辨率土地覆盖类型数据集,见图2(b),大坡岭流域内草原和耕地所占的面积比例较大,说明流域内以人工种植的植被为主,各植被类型对应的特定参数主要依据LDAS 提供的值来确定。
(4)土壤数据。选取了1 km分辨率的基于HWSD的中国土壤数据集及FAO 世界粮农组织的5′分辨率的土壤质地分布数据集,VIC模型上(下)层土壤类型根据HWSD数据库确定,如图2(c)、(d)所示,可见大坡岭流域上层土壤以黏壤土和砂质黏壤土为主,下层土壤以黏壤土为主。
3 流域应用
3.1 参数敏感性分析
在制备土壤参数时发现,VIC模型的部分水文参数(表1)依托于概念性产流模型,缺乏实测数据,需要通过经验估计或参数率定来确定取值。在众多有关VIC 模型的研究应用中,对模型参数的敏感性分析研究相对很少[20]。鉴于不同参数对模拟效果有不同程度的影响,探究模型参数的敏感性,仅选择敏感参数进行率定,对提高模型应用效率具有重要意义。

表1 部分土壤参数及其取值范围Tab.1 Some soil parameters and their value ranges
本文使用LH-OAT 敏感性分析方法对这8个参数进行敏感性分析,设置m=5(即将参数的空间分布等分为5 层),fi= 0.1(即每个参数的微小变化设置为0.1)。选用纳什系数(NSE)、相对误差(RE)、高水量误差系数(fg)及低水量误差系数(fd)共4个评估指标来评估各个参数对日径流过程的敏感性。4个评估指标的计算公式如下:
式中:Qc(i)为计算流量;Qob(i)为实际流量;N为模拟的序列长度。
本文针对不同参数,对其敏感性按从大到小进行了排序(表2),并将敏感度划分等级,分别是:排序为1 的是极敏感;排序为2~7 的是较敏感;排序为8 的是不敏感[21]。最后综合统计各参数在不同指标下的最小排序值作为其全局敏感性的排序结果。
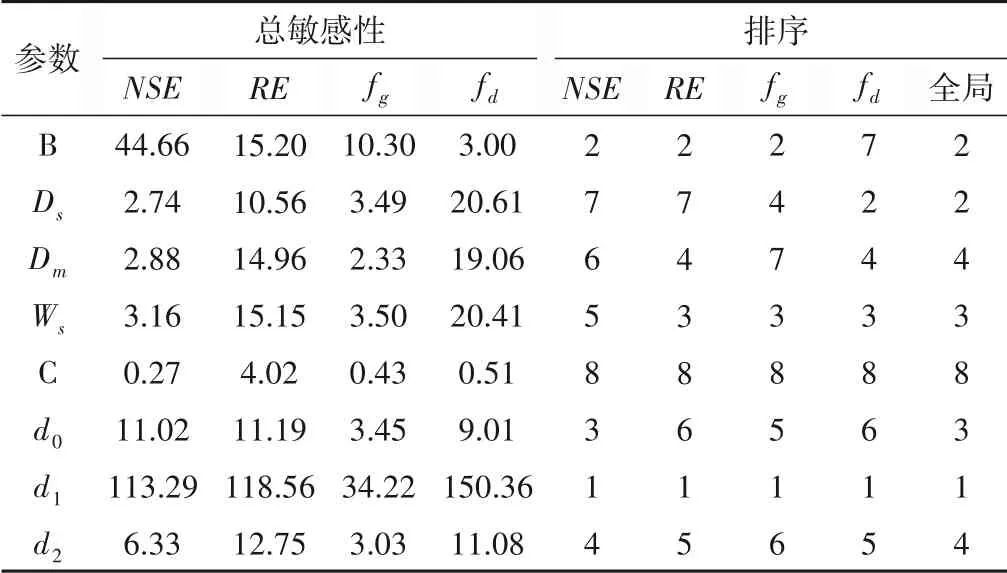
表2 VIC模型参数敏感性分析结果Tab.2 Parameters sensitivity results of the VIC model
由表2可以看出,参数d1(上层土壤厚度)在4 个指标下均为最高敏感度,即d1是最敏感的参数。在VIC 模型中,上层土壤厚度直接影响上层土壤含水量与裸土蒸发,从而影响直接径流的产生,因而d1对模型的敏感性较高。
对于关注高流量值的评估指标fg来说,蓄水容量曲线参数B 的敏感性较高,为较敏感参数。参数B反映了流域下渗能力空间分布的不均匀性,对产流过程影响巨大。大坡岭流域面积虽不大,下垫面分布不均匀性却较为明显,所以B对产流较敏感。
参数Ds(非线性基流发生时占最大基流比例)、Dm(最大基流量)、Ws(非线性基流发生时占最大土壤含水量比例)、d0(顶薄层厚度)和d2(下层土壤厚度)对产流起间接影响,全局敏感性均为较敏感。其中,参数Ds、Dm和Ws与模型基流计算有关,Dm通过影响基流量大小从而影响径流,Ds和Ws与非线性基流有关,这3个参数在低水量径流计算中敏感性较高,说明结果与实际水文过程较为相符。d0影响顶薄层湿度和裸土蒸发,一般在模型运算时设置为缺省值0.1 m,但从结果来看,其对径流模拟效果有一定的影响。
参数C在4 种指标下均表现为不敏感,说明该参数对模型模拟结果的影响不大,在模型运行开始时设置经验值即可。
本研究的结果与张续军[15]和宋星原[22]的结果较为接近。张续军认为d1对多年径流相对误差较为敏感,B 对日径流过程拟合程度较为敏感。宋星原认为d1、Ws和B 对径流相对误差敏感度相对较高,对于纳什系数,d1的敏感度远高于其他参数。
综上,VIC 模型土壤参数中的B、Ds、Dm、Ws、d0、d1及d2这7个参数较为敏感,在后续研究中应注重考虑率定优化,参数C为不敏感参数,本文便不对其进行率定,设置为固定值2。
3.2 理想模型应用
为检验系统微分响应参数率定方法(SRPCM)在VIC 模型中的适用性,构建VIC 理想模型进行单参数率定检验。本文随机设置一套参数真值(表3),将实测输入数据和参数真值代入到VIC模型计算得到的流量过程即为“实测径流”。文中通过率定单参数来验证SRPCM 的应用效果,根据上节敏感性分析结果,选择土壤参数中B、Ds、Dm、Ws、d1及d2这6 个参数进行参数优化(因考虑到模型将d0设置了缺省值0.1 m,且在后续运行时发现当d0>d1时会终止计算,故本文将此值设置成默认值,不再进行率定)。

表3 理想模型参数真值Tab.3 The real value of ideal model parameters
图3为分别对6 个参数率定时,各参数初始值和最优值的分布,其中,平均迭代次数最多的为参数d2,共迭代4次,单组迭代次数最多的是d2第五组,共迭代7次。从图3可以看出,对于随机给定的不同初值,各参数经过优化均能收敛到表3的真值。可见,SRPCM 在VIC 理想模型单参数率定中具有一定的适用性,且具有高效、稳定、结果合理的特性,说明将此方法应用于VIC模型是可行的。
3.3 实际流域应用
参数率定及验证数据资料选用了大坡岭流域2006-2016年共11年的日径流数据。根据VIC模型参数率定原则,选择2006年为预热期,模拟结果不计入目标函数,2007-2014年为率定期,2015、2016年为验证期。实测流量数据为大坡岭水文站日流量过程。
本文使用系统微分响应参数率定方法进行参数率定,为防止迭代过程陷入死循环,设置最大迭代次数为500次,以纳什系数(NSE)作为目标函数,率定结果见表4。

表4 大坡岭流域参数率定结果Tab.4 The parameter calibration results of Dapoling catchment
本文仅进行了水量平衡模拟,率定期和验证期的纳什系数(NSE)和径流总量相对误差(RE)见表5,从结果可以看出,VIC模型对大坡岭流域的模拟效果较好,率定期和验证期的径流总量相对误差分别为4.64%、7.09%,均控制在8%以内,径流过程的纳什系数分别为0.600、0.601,均达到了0.6,验证期的NSE略高,据此可以看出采用系统微分响应参数率定方法优选的VIC模型参数,对于大坡岭流域的日径流过程模拟具有较好的适用性。

表5 大坡岭流域径流模拟效果Tab.5 Runoff simulation results of Dapoling catchment
图4点绘了率定期与验证期日流量模拟值与实测值的散点图,可以看出在率定期和验证期,绝大部分散点比较均匀分布在对称线的两侧,但在高流量段,不论是率定期还是验证期,都有几个散点位于偏右下的位置,说明在日径流模拟过程中,VIC模型对于流量峰值段的模拟结果偏小。率定期和验证期的相关系数分别为0.790 7、0.811 7,线性回归系数R2分别为0.625 3、0.658 9,相较于率定期,验证期的模拟效果均有所提高,这表明采用系统微分参数率定方法得到的最优参数值具有一定可信度,该方法适用于VIC模型参数率定。
对比率定期及验证期流量过程线(图5、图6)可知,模拟与实测径流过程总体拟合度良好,特别是洪峰出现时间和退水时间的模拟基本与实测径流过程相一致。但对于部分较大的流量峰值(特别是2008年、2014年及2015年等日径流峰值段),模拟结果不是特别理想,在流量峰值时模拟值基本偏小,这与上文图4散点图得出的结论相一致。分析其原因,可能与模型本身参数和结构的局限性、研究区域偏小以及收集的资料缺乏代表性等因素有关。
4 结 语
本文采用LH-OAT 方法对VIC 模型参数进行敏感性分析,将系统微分响应参数率定方法与VIC模型结合并应用于大坡岭流域,得出以下结论:①VIC模型的敏感参数以上层土壤厚度d1为主,模型参数的敏感性分析,对后续参数率定具有一定的参考价值;②理想模型和实际流域的应用检验表明,用系统微分响应参数率定方法率定VIC模型参数是可行的,率定结果合理、高效;③将该方法率定VIC 模型敏感参数的结果应用于大坡岭流域,取得了较好的应用效果,但对径流过程中的较大洪峰模拟效果不是十分理想,可能与模型本身的局限性等原因有关,值得未来进一步的研究与改进予以提高水文模拟精度。□
