指向数学学科核心素养的可视化教学
2021-12-29岳峻



当今,“互联网+教育”成为数学教学的必然之举。中学数学教学须倡导以超越课堂面授的陪伴为途径、以提升数学核心素养为宗旨、以锤炼数学思维为核心的谋略式培育。可视化无疑是一项行之有效的策略。林崇德认为:“核心素养具有可教、可学的外显部分,同时也存在无声、无形,但可感、可知的内隐部分。”[1]核心素养的外显部分,亦即知识层面,可以借助一些形式“教”出来;而内隐部分,亦即思想层面,只有在教学过程“玩”数学中慢慢地渗透,只有在学习过程“玩味、联想”中才能“悟”出来。如何借助可视化技术,提升学生的数学核心素养?笔者应用GeoGebra软件,“仰望星空,脚踏实地”,做了一些教学层面上的实践。
一、数学可视化与GeoGebra动态演示工具
数学可视化就是将抽象的数学学习对象(概念原理、结构关系、思想方法等)用可看见的表征形式(图形、图象、动画等)清楚直白地呈现出来,使人们对数学学习对象有一个形象、直观、整体的认识和理解[2]。
在数学可视化教学中,教师借助“形”的“图示”与“数”的“析理”、构图元素的“隐藏”与“虚实”、曲线的“色彩”与“动画”等,通过信息技术手段进行表征,可以建立“可视”与“抽象”之间的内在联系,突破“只可意会,不可言传”的交流障碍。这是理解信息元素的交互、洞悉数学本质的美感的好办法,也是提升学生数学核心素养的捷径。
GeoGebra软件是数学可视化的重要“云梯”,是数学教学中的“诗意催化剂”。教师借助GeoGebra软件可进行“形”与“数”的自由转换,建立“可见形式”与“抽象形式”的直接联系。该软件的应用拓展了数学的学与教的空间,有效地改进了“诱思探究”的方式,有利于激发学生潜能,调动学生读懂数学“玄妙”的渴望,提高学与教的有效性,实施更多具有探索性的数学实验。GeoGebra软件是教师课堂教学的动态演示工具,也是学生自主学习、探究“遨游”的“隐形的翅膀”,其手机版的推广更为学生课后深度学习、思维深化,提供了在“玩”数学中进行数学实验的空间。寓教于乐是该软件保持活力的关键所在。
二、数学可视化提升数学核心素养的实践
数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等六个方面。在知识模块的教学中,教师可以渗透一项或多项素养的培养。在GeoGebra软件的支持下,指向学科核心素养培养的教学融合度和效能将大大提高。笔者结合实例侧重从如下几个方面阐述思路与做法。
(一)透彻理解数学概念,提升数学抽象素养
数学概念是数学学科的灵魂和精髓,是数学课程“四基”和“四能”教与学的核心。学生掌握数学概念才能形成对数学的基本的、概括性的认识。数学概念教学有赖于学生对数学概念的透彻理解。GeoGebra软件支持“人机交互”数学实验,可帮助学生高效理解数学概念,助力学生在情境中用数学眼光“看”世界,抽象数学概念和思想方法,积累从客观到主观的活动经验;养成观察问题、思考问题的素养,用数学思维“探”世界,把握事物的本质,以简驭繁;运用数学抽象的思维研析问题、思考问题,进而提升直观想象和数学抽象素养。
【例1】异面直线的理解:不同在任何一个平面内的两条直线。
理解:选取直线工具构建异面直线,,选取旋转工具使得经过直线的平面绕直线旋转,并构建滑动条,拖动滑动条改变旋转角度的大小。仔细观察发现:无论如何旋转平面都不会经过直线(如图1)。
同理,经过直线的平面也无论如何不会经过直线。
【例2】导数的几何意义:设曲线上一点(, ()),过点的一条割线交曲线于另一点( +Δ, ( +Δ)),如图2所示,则割线的斜率为:
。
当点沿曲线向点运动,并无限靠近点时,割线的斜率逼近的切线的斜率,即当 Δ无限趋近于0时, 无限趋近于点处的斜率,有:
理解:首先,在指令栏输入指令 ()=- 3
+2+ ,选取直线工具构建割线,选取切线工具构建曲线在点处的切线,选取斜率工具分别求出切线、割线的斜率;然后,选取文本工具分别创建相应的文本,选取移动工具拖动点的位置,使之无限逼近点,观察割线的斜率的变化;最后,选取移动工具拖动点的位置,观察点处的切线与曲线公共点个数(如图3)。
感悟:异面直线是立体几何教学的“说不清道不明”的数学概念。以往不管教师怎么阐述总是词不达意,学生因刚接触空间对象,直观想象素养有待于强化,理解起来颇有“行走在云端”之感。教师借助GeoGebra软件的“3D功能”进行动态演示,让学生对这一概念能轻松、透彻理解。导数的几何意义涉及无限逼近思想,数学可视化使学生在操作体验中,经历变化率从“平均”到“瞬时”、直线从“割”到“切”的过程,增加了更多的真实体验。学生感知割线“无限逼近”与“量变到质变”的哲学思想,实现“向技术学习”,这是传统教学无法做到的。在导数的几何意义的动态演示中,教师还可以引导学生观察曲线的切线的不同形式,认识到切线与曲线的公共点未必只有一个,真正地理解切线的数学本质。
(二)高效破解教学难点,提高数学思辨能力
高效破解难点是衡量教师教学素养的标尺。教学难点之所以成为难点,原因在于数学的抽象不易理解,或者推理的技能技巧不易掌握,又或者是模型的构建经验不足。
数学思辨能力指学生通过对数学对象进行分析、思考、推理和辨析等思维活动,透彻认知数学知识的能力,包括准确分析、明晰推理和清楚表达三项具体要素。《普通高中数学课程标准(2017年版)》所设定的核心素养的本质就是抽象、推理和模型[3]。“抽象、推理和模型”对应的哲学思考就是“三会”,而直观想象、数学运算、数据分析已经融入“抽象、推理和模型”之中“结伴而行”。明晰推理就是数学思辨素养追求的目标,模型意识是数学思辨素养表达层面的四项要素之一。
数学可视化可以帮助学生破解学习过程中的难点,还能帮助教师高效地提高课堂教学的专业素养。GeoGebra软件是一个超级“数学实验室”。教师应用该软件建立几何直观与抽象概念之间的印证关系,体现知识的多元联系,体现实证与抽象的和谐统一,让学生体验发现的乐趣和欣喜,实现数学教学与信息技术的高度融合,有效地破解了传统教学遇到的困局,弥补了传统教学方式的不足,减轻了学生的认知负荷。
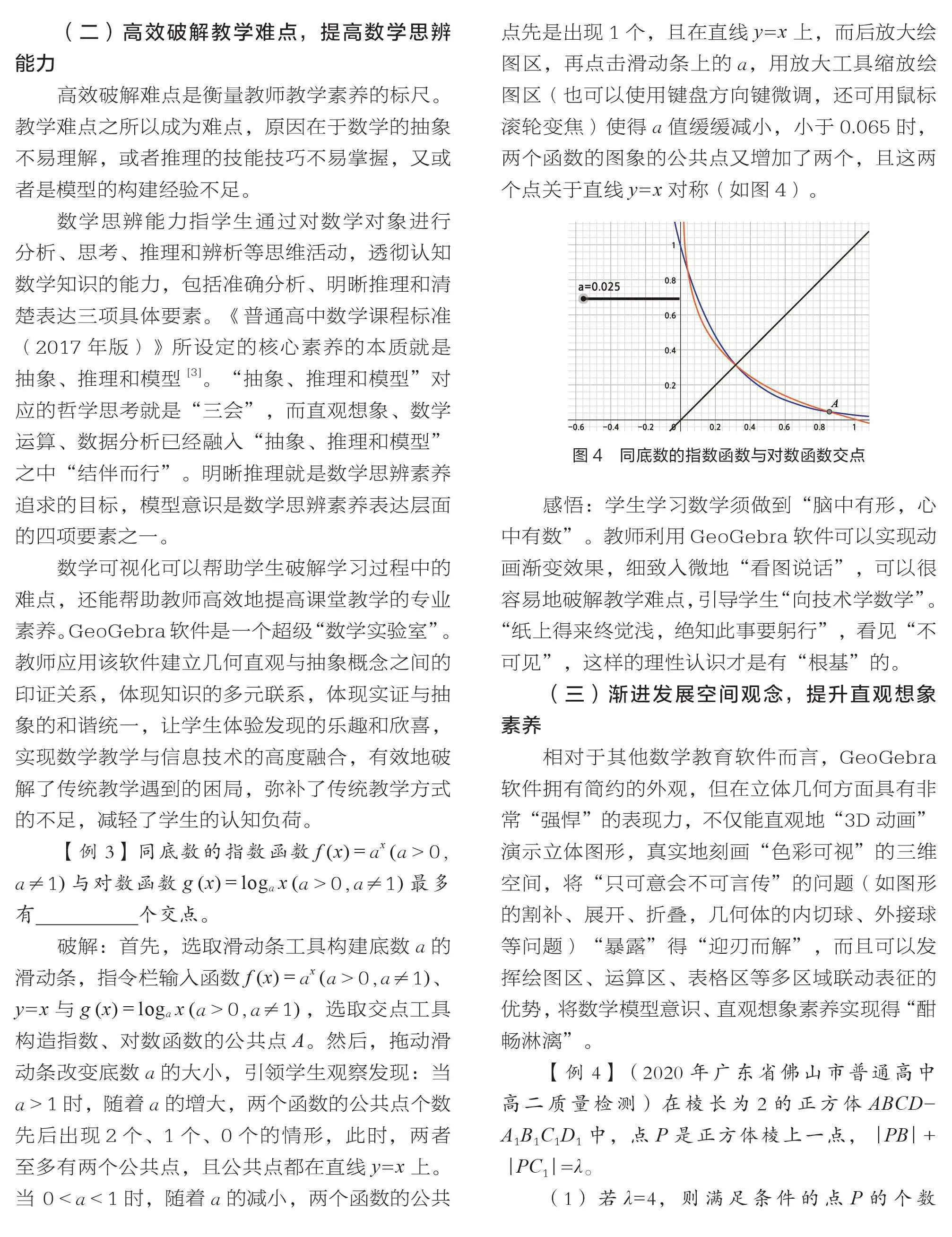
【例3】同底数的指数函数 () = (>0, ≠1)与对数函数 () = log (>0,≠1)最多有 个交点。
破解:首先,选取滑动条工具构建底数的滑动条,指令栏输入函数 () = (>0,≠1)、=与 () = log (>0,≠1) ,选取交点工具构造指数、对数函数的公共点。然后,拖动滑动条改变底数的大小,引领学生观察发现:当>1时,随着的增大,两个函数的公共点个数先后出现2个、1个、0个的情形,此时,两者至多有两个公共点,且公共点都在直线=上。当 0<<1时,随着的减小,两个函数的公共点先是出现1个,且在直线=上,而后放大绘图区,再点击滑动条上的,用放大工具缩放绘图区(也可以使用键盘方向键微调,还可用鼠标滚轮变焦)使得值缓缓减小,小于0.065时,两个函数的图象的公共点又增加了两个,且这两个点关于直线=对称(如图4)。
感悟:学生学习数学须做到“脑中有形,心中有数”。教师利用GeoGebra软件可以实现动画渐变效果,细致入微地“看图说话”,可以很容易地破解教学难点,引导学生“向技术学数学”。“纸上得来终觉浅,绝知此事要躬行”,看见“不可见”,这样的理性认识才是有“根基”的。
(三)渐进发展空间观念,提升直观想象素养
相对于其他数学教育软件而言,GeoGebra软件拥有简约的外观,但在立体几何方面具有非常“强悍”的表现力,不仅能直观地“3D动画”演示立体图形,真实地刻画“色彩可视”的三维空间,将“只可意会不可言传”的问题(如图形的割补、展开、折叠,几何体的内切球、外接球等问题)“暴露”得“迎刃而解”,而且可以发挥绘图区、运算区、表格区等多区域联动表征的优势,将数学模型意识、直观想象素养实现得“酣畅淋漓”。
【例4】(2020年广东省佛山市普通高中高二质量检测)在棱长为2的正方体-中,点是正方体棱上一点,丨丨+丨丨=。
(1)若=4,则满足条件的点的个数为 ;
(2)若满足丨丨+丨丨=的点的个数为6,则的取值范围是 。
发展:选取正六面体工具构建正方体-,构建直线与平面,在该平面内选取一点,并构建焦点分别为,,经过点的椭圆;创建绘图区2,构建底数=的滑动条,将椭圆绕直线旋转角度,在指令栏输入序列指令构建椭圆序列,输入曲面指令构建椭球面,并选取复选框工具创建相应的复选框;移动点改变椭圆的大小,观察椭球面与正方体的各棱的交点个数,进行如下演示。
(1)若2 <<4,如图5所示,可得点的个数为6。
(2)若=4,点的个数为4。
(3)若4<<2+2 ,点的个数为4。
(4)若=2+2 ,点的个数为8。
(5)若2+2 <<4 ,点的个数为6,如图6所示。
(6)若=4 ,点的个数为2。
(7)若>4 ,点的个数为0。
感悟:数学可视化蕴含着神奇、孕育着创造。动态解析立体几何问题是教与学的难点,它渗透着“动”与“静”的哲学思想和直观想象素养的培养。教师借助GeoGebra软件将抽象的立体几何问题用“看得见”的多种表征形式呈现出来,虚实清晰,层次鲜明。学生感叹:GeoGebra软件就是数学魔术师。
(四)多维启迪问题探究,积累基本活动经验
数学学习的成效如何,教师需要对学生学业水平进行检测。学生对数学知识的掌握往往通过分析问题、解决问题来完善和体现。数学问题是锤炼数学思维的重要载体。解题教学非常重要,在增强创新意识,认识数学的科学价值、应用价值,树立善于思考、严谨求实的科学精神等方面有积极作用。GeoGebra软件充当超级“数学实验室”的角色,让学生拥有动手操作的愉悦感受,经历“感知—感悟—新知”“实验操作—大胆猜想—推理验证”的过程,养成良好的数学学习习惯,将获取知识的经验转化为认识世界的智慧。
【例5】(2019年浙江卷)已知点 (1, 0)为抛物线2=2 ( >0)的焦点(如图7)。过点 的直线交抛物线于,两点,点在抛物线上,使得△的重心在轴上,直线交轴于点,且在点的右侧,记△, △的面积分别为,。
(1)求的值及抛物线的准线方程;
(2)求 的最小值及此时点的坐标。
启迪1:已知=2,抛物线方程为2=4,其准线方程为=-1。
首先,在运算区,设过点的直线的方程为=+1,代入抛物线方程得2-4-4=0。
设 (,), (,)则+= 4,= -4,+= (+)+2=42+2。
设(,),由于△的重心在轴上,则 ,即=-4。
因为= =42,所以 。
因为在点的右侧,所以在点的右侧, >1,即2> 。
为了研究的需要,需满足=-4,2> 。
启迪2:教师应用GeoGebra软件,首先,在指令栏输入抛物线的方程,以及直线的方程=+1,并创建的滑动条,设置范围 ,步长为0.001;然后,构建△及其重心,选取面积工具分别计算出△,△的面积,;最后,创建绘图区2,在指令栏赋值=,= ,构造点,选取文本工具创建文本与的比值,拖动滑动条可以发现“牵一发而动全身”。结合动画演示,可以“看”到比值 的变化,并“慢动作”地寻求 最小值为1.866时,=0.707。
启迪3:=0.707是近似值,准确值是多少呢?它是哪个常见实数的近似值呢?是 吗? 最小值1.866呢?是1+ 吗?
感悟:数学实验旨在让学生“知其然”,帮助学生直观感知,培育学生的合情推理的素养,但“知其所以然”尚需推理论证,这个数学化过程则是培育学生形成数学思维、锤炼逻辑推理素养的极好路径。两者之间需寻求恰当合理的动态均衡,各得其所,一体考量方能相得益彰。
三、总结
数学核心素养是新课程教学改革深化的重大成果,基于GeoGebra软件进行数学可视化教学是提升数学核心素养的重要途径,有着巨大的应用空间,还有待于在学习中挖掘,在教学中熟练,在探究中提炼。只有将信息技术深度融合于数学内容中,并将可视化操作从教师手中转移到学生手中,才能实现从形式到内涵的转变。学生通过直观感知,展开想象,通过操作积累基本活动经验,逐渐提升数学核心素养。
当然,数学是以计算和推理为主的一门学科,数学可视化仅是教学的辅助手段,不能为“可视化”而可视化,应该在学生独立思辨、拥有困惑的基础上,对手动难以作图或用语言难以表述清楚的内容进行及时展现,解惑。
“马不伏历,不可以趋道;士不素养,不可以重国。”数学核心素养是学生先天条件和后天学习的综合素质的体现。数学核心素养如何培养呢?t0yklyCwtJNLIM7S0JxChwz+7sMervwhJWQyP6xHCso=正如史宁中教授所言:“信息技术正在通过与学科的融合来改造我们的教学,形成一种全新的教学模式。”[4]基于GeoGebra软件的数学可视化之路,必然是提升数学核心素养的有效路径之一。广大同仁且行且探索。
注:本文系安徽省教育信息技术研究课题“基于GeoGebra的数学实验与可视化教学的实践研究”(立项号:AH2019210)的阶段性成果;阜阳市教育科学规划课题“核心素养下高中数学教学中学生反思能力有效性实践的研究”(立项号:FJK043)的成果。
参考文献
[1] 李金聪.核心素养视角下离心率试题的命制与评价[J].福建中学数学,2018(1):3-5.
[2] 张志勇.高中数学可视化教学:原则、途径与策略——基于GeoGebra平台[J].数学通报,2018(7):21-24.
[3] 刘祖希.访史宁中教授:谈数学基本思想、数学核心素养等问题[J].数学通报,2017(5):3-7.
[4] 祝元志,牟艳娜.深度融合信息技术,提升小学数学教学魅力[J].中小学数字化教学,2019(11):5-8.
(作者系安徽省太和中学高级教师,华中师范大学考试研究院特聘研究员)
责任编辑:祝元志
