基于综合形态算法的变压器励磁涌流识别方法

2021-12-29张运驰高厚磊杜士昌

电力系统自动化 2021年24期

张运驰，高厚磊，杜士昌

（1. 电网智能化调度与控制教育部重点实验室（山东大学），山东省济南市 250061；2. 山东鲁圣电气设备有限公司，山东省日照市 276800）

0 引言

励磁涌流的识别在变压器差动保护中占据非常重要的地位，其识别效果及速度直接决定了差动保护的性能。早期励磁涌流的识别有二次谐波制动、间断角原理、波形相关性等方法［1-3］，已在实践中被广泛应用。然而，随着电网复杂度的不断提高，上述方法在某些情况下变得不再适用［4-7］。

关于励磁涌流的识别主要集中在两个方向。一是对变压器的等效方程和参数进行研究，如基于磁通特性［8］、等效电感［9-10］、瞬时无功功率［11］等方法，此类方法需要同时获得电流电压数据，实际应用中会增加保护的复杂程度。另一方向是仅针对电流量的识别，主要通过分析电流的电气特征或波形特征对涌流和故障电流进行区分。电气特征主要有基于负序分量［12］、衰减直流分量［13］、非周期分量［14］，此类识别方法可以实现保护的快速闭锁，但往往会受电流互感器（TA）饱和的影响。波形特征类识别方法则是通过识别励磁涌流的尖顶波特性与故障电流的基波正弦特征对两者进行区分，由于其原理简单、容易实现，以此为基础的研究非常广泛，常结合能够表征波形间差异的数学方法［15-16］或利用小波分析、数学形态学、人工智能方法等对波形特征进行识别［17-19］。

数学形态学本身不涉及复杂的数学运算，由于其完全在时域中分析和处理信号，且在数据窗、相移和幅值衰减等方面具有优势［20］，也用于识别励磁涌流。现有利用数学形态学识别励磁涌流的方法主要分为两类：一类是通过滑动数据窗对电流波形进行处理［18，21-22］，此类方法的特点与基于电气特征的识别方法类似；另一类是利用固定数据窗［23-29］，仅对窗内数据进行分析。这些方法大都需要一个工频周期的采样时间才能对故障电流和涌流进行区分，且对于带有较大剩磁的空载合闸、空合于内部轻微匝间故障以及考虑TA 饱和等特殊工况，判据可能无法正确识别。文献［26］提出利用加权形态滤波算子提取差动电流的正弦特征，采用相关性系数作为判据识别和应涌流，仅需半个工频周期的数据窗，但整体上存在一个工频周期的延时并且在内部故障发生TA 严重饱和及空合于内部轻微匝间故障时可能会误闭锁。文献［27］利用形态学方法提取波形骨架，根据不同工况下骨架的特点快速、可靠地识别涌流和故障，但每计算一个骨架点都需要进行一次形态学运算，运算量较大。文献［29］首先利用形态学峰谷检测识别多数和应涌流，考虑发生TA 饱和的特殊情况，利用形态梯度与加权形态滤波算子处理半个工频周期的差动电流，并采用相关性系数作为判据，方法简单、适应能力强，但需要一个工频周期的采样时间，且空合于内部匝间故障时可能会误闭锁。

本文在文献［29］利用形态梯度与加权形态滤波算子处理差动电流思路的基础上，对形态梯度运算进行改进，并通过对比梯度信号与滤波结果，提出了2 个积分型判据：判据1 可以减少大多数故障情况下识别所需的采样时间和计算量；判据2 则是为了保证特殊工况下方法的可靠性。所提方法计算负担小，无须峰谷检测等其他方法的配合，可以实现励磁涌流的可靠闭锁以及内部故障时的快速动作。最后，不同情况下的仿真结果验证了所提方法的性能。

1 差动电流的形态学处理

1.1 数学形态学

数学形态学本质是对集合进行的操作，当其处理一维函数信号时，就有了灰度形态学［30］。灰度形态学中，基本形态学运算腐蚀和膨胀的定义为：

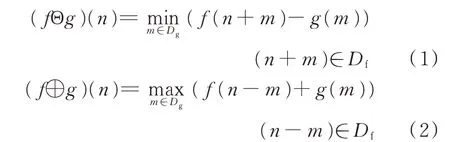
式中：Θ 为腐蚀运算符；⊕为膨胀运算符；f为输入信号，定义域为Df；g为用于“扫描”输入信号的结构元素，定义域为Dg；m、n分别为结构元素和输入信号的离散采样点序号。

基本形态梯度算子G(n)为：

在基本形态梯度运算的基础上，通过改变结构元素的长度以及原点位置形成多分辨形态梯度［31］。多分辨形态梯度运算的结构元素形式通常为：

式中：g+和g-分别用来提取信号的上升沿和下降沿；下划线处为结构元素原点。

多分辨形态梯度仅进行一级运算时有：

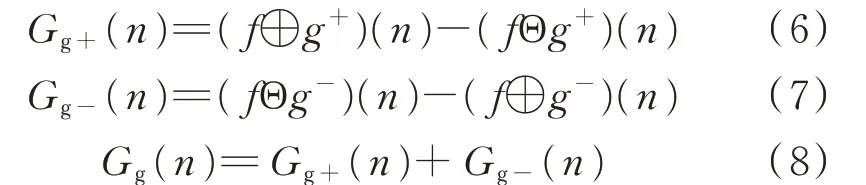
式中：Gg+(n)、Gg-(n)分别为提取到的第n个上升沿和下降沿信号值；Gg(n)为得到的第n个一阶梯度值。

1.2 形态学方法的应用

理论分析和实测数据表明，内部故障时故障相的差动电流（以下统称为故障电流）是含有衰减直流分量的正弦波，其基波相似性强。当差动电流为励磁涌流时，其间断角特性、尖顶波特性明显，存在大量的非周期分量和高次谐波分量，如附录A 图A1中蓝色曲线所示。

本文利用数学形态学方法处理差动电流，以表征其基波相似性的强弱。在加权形态滤波［32］中，定义了加权腐蚀和膨胀算子，分别为：

加权形态滤波算子DWG(n)表示为：

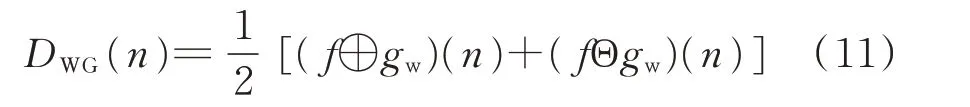
式中：gw为关于原点对称的正弦结构元素。

利用加权膨胀和腐蚀算子，分别根据式（6）、式（7）构造改进形态梯度算子，其结构元素g+和g-分别为：

式中：ω为基波频率；Δt为采样间隔；γ+1 为结构元素长度。

假设待处理信号为故障电流，有第n点的采样值为：

式中：θ为相角；τ为时间常数；A、B分别为周期分量和衰减直流分量的幅值。

令α(n)=ωnΔt+θ，不考虑式（14）中的直流分量时，将周期分量与式（12）一起代入式（6），得到：

同理，将式（13）代入式（7），得到：

结构元素确定后γ为定值，此处结构元素的长度选为Nc/20，Nc为一个工频周期的采样点数。式（15）、式（16）相加得到幅值与结构元素长度有关、相位超前于故障电流周期分量90°的正弦信号，可见改进梯度运算后仍保留了原信号的基波相似特性。由于非周期分量满足B≤A且在一个结构元素的跨度内变化很小，非周期分量也仅会使信号局部产生细微的差别，最终得到的梯度信号Gg(n)如附录A 图A1（a）中绿色曲线所示（Nc=80，结构元素长度为4），基波相似性较强。

若待处理信号为励磁涌流，显然其基波相似性较差，如附录A 图A1（b）中绿色曲线所示。得到Gg(n)后，进行加权形态滤波处理［26］，式（11）中gw取{cos(pωΔt)，cos((p-1)ωΔt)，…，1，…，cos((p-1)ωΔt)，cos(pωΔt)}，p为正整数，gw的长度取Nc/8或Nc/8-1，取奇数，得到滤波结果DWG(n)如附录A 图A1 中红色曲线所示。

2 算法的提出

2.1 波形特征分析

经过梯度处理后，故障电流的形态滤波与梯度运算结果基本相同；而对于基波相似性较差的励磁涌流，奇异性会增强，与滤波后的结果有较明显的差异。

如图1 的仿真结果所示，最初一段时间内，励磁涌流和故障电流波形在某些情况下很难区分［33］，原始信号首峰值之前的结果具有相似性（黑色方框），其后二者便出现明显的不同（红色圈），故障电流的Gg(n)与DWG(n)之间的差值很小，而励磁涌流的差值则较大。由图1 可以看出，故障电流和涌流的处理结果在原始信号首峰值之后的第一梯度极值点处差异明显，记该点为K0，可以该点为中心确定一个计算短窗，以表示Gg(n)与DWG(n)之间的差异。

图1 不同合闸角下故障电流和励磁涌流的差动电流计算结果Fig.1 Differential current calculation results of fault current and inrush current with different closing angles

考虑内部故障发生TA 饱和以及空载合闸于内部轻微匝间故障的情况，在K0点附近Gg(n)与DWG(n)的值相差也非常明显，仿真结果如图2（a）及附录A 图A2 所示。针对此类特殊情况，由于TA 饱和时，电流在前1/5～1/4 工频周期内不会立即饱和，仍保持近似正弦波的特征；空合于内部轻微匝间故障时，电流波形是故障电流和涌流的结合，在涌流的间断期间同样呈现近似正弦的特征。因此，可以寻找保护启动前电流的突变点，延后一个工频周期将该点记为K1，可以看出，内部故障发生TA 饱和与空合于内部轻微匝间故障时，K1附近的Gg(n)与DWG(n)差别很小，而对于励磁涌流，两者在K1处仍有很大差异，仍可以被正确识别，如图2（b）所示。

图2 特殊情况下故障电流与励磁涌流的差动电流计算结果Fig.2 Differential current calculation results of fault current and inrush current in special cases

2.2 判据的设计

基于上述分析，本文在K0处确定了一个计算短窗，在窗内针对Gg(n)与DWG(n)的差值构造积分型判据，该判据对于大多数情况的内部故障仅需不足一个工频周期的数据即可识别，记为判据1：

式中：k为所取短窗的宽度；i为短窗内的采样序号。综合识别时间和仿真效果，取k=Nc/16；M为从算法启动到K0之间|Gg(n)|的最大值，引入M使判据归一化，不受原始信号幅值的影响。

由式（17）可以看出，算法对采样率有最低要求，智能变电站的采样频率一般为4 kHz，本文方法完全适用。K0取为Gg(n)首个过零点之后的第一极值点，该点附近的Gg(n)与DWG(n)值相差较为明显。设判据1 整定值为δ1，set，若δ1＞δ1，set，则判断为励磁涌流，反之为故障电流。

考虑2.1 节中特殊情况下也会出现δ1＞δ1，set的情况，判据1 会误判为励磁涌流，故以K1为起始采样点构造积分型判据2 将判据1 误闭锁的保护开放，对励磁涌流则继续闭锁，判据2 为：

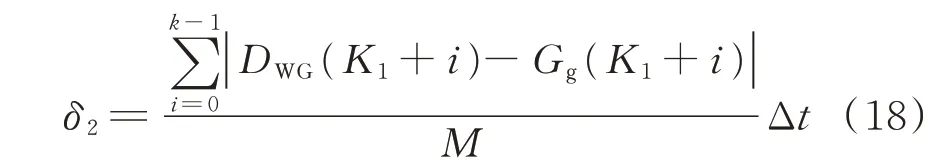
设判据2 整定值为δ2，set，若δ2＞δ2，set，则判为励磁涌流，继续闭锁，反之立刻开放保护。两判据对应的短窗算法如图2 所示，图中虚线框包围的部分分别为判据1 和判据2 的计算数据窗，判据1 以K0为数据窗中点，判据2 以K1为数据窗起点，数据窗宽度均为5 个采样点。

3 算法的协同逻辑与流程

算法的启动逻辑设定为保护启动之后，从满足保护启动判据的第1 个点开始，判断三相差动电流是否有连续3 个采样点的绝对值大于差动保护整定值，启动点选为3 个连续点中的第1 个。若某相电流满足条件则执行识别算法，若半个工频周期后仍不满足条件，则该相输出δ1=0，记算法启动点为k0。

数据窗的选择方法是，算法启动之后，寻找原始信号的首峰值点km，对应于Gg(n)的首个过零点，在该点之后找到原始信号斜率绝对值最大的点，对应于Gg(n)的极值点，斜率以两点之差代替。考虑到计算短窗的存在以及形态学运算的端点效应［21］问题，延后采样Nc/8。端点效应是很多研究忽视的问题，只要利用结构元素进行形态学处理，就需要一个与结构元素等长的采样裕度。判据1 中取采样点序号(k0-Nc/20)和(K0+Nc/8)之间的电流进行梯度运算，取采样点序号(K0-Nc/8)和(K0+Nc/8)之间的梯度信号进行滤波运算。对于判据2，梯度运算及滤波运算均取采样点序号(K1-Nc/8)和(K1+3Nc/16)之间的数据。算法协同判断逻辑如下。

1）保护启动元件动作后，首先闭锁差动保护，分别判断三相差动电流是否满足算法启动条件，满足则进行判据1 的判断，不满足则输出S1=0，S1为判据1 输出结果。

2）对于判据1，三相差动电流中满足δ1＞δ1，set的相输出S1=1，不满足的输出S1=0。若有两相及以上的S1等于1，则继续闭锁差动保护；反之，判断为内部故障电流，快速开放保护。

3）对于判据1 闭锁的信号执行判据2，同样三相差动电流中满足δ2＞δ2，set的相输出S2=1，不满足的输出S2=0，S2为判据2 的输出结果。将各相信号的S2和S1相“与”，若有两相及以上的结果等于1，则识别为励磁涌流，继续闭锁差动保护；反之，立刻开放保护。

整定值范围保守选取δ1，set∈[20，80]，δ2，set∈[20，80]，算法整体流程如图3 所示。

图3 算法流程图Fig.3 Flow chart of algorithm

4 仿真分析

为验证本文所提算法的有效性和可靠性，利用PSCAD/EMTDC 仿真软件搭建模型并进行故障仿真。建立的系统如图4 所示，其中有2 台参数、接线完全相同的双绕组变压器，容量100 MVA、变比230 kV/35 kV、YNd11 接线、短路阻抗12.96%、空载损耗1%、铜耗2%；一台空载，另一台经50 km 长的线路L 给90 MVA 负荷供电，线路选用频变参数线路模型；利用受控直流源模拟剩磁，根据变压器的磁通-电流曲线，以附加直流电流的方式模拟剩磁；利用三绕组变压器一、二次绕组短接来模拟双绕组变压器，以实现匝间或匝地故障；系统频率50 Hz，采样频率为4 kHz，电流互感器二次额定电流为5 A。

图4 仿真系统图Fig.4 Simulation system diagram

综合所建立模型以及差动保护的整定，算法启动值设为2 A，与差动整定值相等；判据整定值选择为δ1，set=δ2，set=50。

4.1 内部故障

首先，不考虑TA 饱和的情况，由于算法为三相综合判据，所以有必要对不同故障类型进行仿真，此外，故障电流最初的波形特征会受故障时刻（以合闸角代替）的影响。因此，针对不同故障类型（单相接地、两相短路、两相接地、三相短路、10%匝间故障、10%匝地故障）以及合闸角（0～180°，间隔15°）进行故障仿真，部分情况下的计算结果见附录B 表B1。其中输出结果“0”表示开放保护，“1”表示闭锁保护。

对于仿真的各种内部故障，协同逻辑下算法均能可靠开放，在所选整定值下，算法仅通过第1 个判据便可以准确识别故障，快速开放保护。此外，计算所得的δ1均远小于整定值，判据的灵敏度较高。

在识别时间上，判据1 对于内部故障的识别时间与波形特征有关，表1 展示了不同内部故障时本文算法所需采样时间的最大（max）和最小值（min），其中tA，tB，tC分别为三相各自所需的采样时间，通过协同逻辑可以得到保护动作所需的采样时间t。

表1 计及端点效应的不同内部故障情况所需采样时间Table 1 Sample time required for different internal fault conditions considering end effects

综合内部故障仿真的各种情况，考虑端点效应所需的采样裕度后，算法识别绝大多数内部故障所需的采样时间在15 ms 以内，部分情况在10 ms 左右。以合闸角90°时发生AB 两相短路为例，A 相差动电流的计算结果见附录B 图B1。本文算法对于该相电流的识别所需时间为9.5 ms，而对于其他多数形态学励磁涌流识别算法，以文献［21］为代表的滑动数据窗类方法能够在8～13 ms 内识别励磁涌流，但其判据为“满足则闭锁”，对于内部故障电流的识别则较慢；而对于文献［29］中所提的固定数据窗算法，由于其需要首先获取峰谷位置，需要一个工频周期的识别时间。再考虑前文所述的“端点效应”问题，现有识别方法所需的时间会更长。而本文算法在考虑了“端点效应”的基础上，通过寻找梯度运算结果与滤波结果差异最大的局部位置对波形进行识别，所提判据摆脱了整个数据窗的限制，且由于算法的三相协同逻辑，使得单相故障时具有更快的识别速度，因而算法在内部故障识别时间上具有一定优势。

4.2 励磁涌流

影响励磁涌流的因素主要是剩磁与合闸角，合闸角会改变涌流的波形特征，剩磁主要影响涌流的幅值和间断角，考虑剩磁为0，0.4Φm，0.6Φm，0.8Φm和0.9Φm（Φm为额定磁通），部分计算结果见附录B表B2。

由仿真结果可以看出，本文所提算法在不同合闸角下都可以正确识别励磁涌流，不受剩磁的影响可靠闭锁保护。以0.6Φm剩磁、0°空载合闸为例，A相差动电流的计算结果见附录B 图B2。考虑“端点效应”的存在，本文算法识别励磁涌流所需时间略大于一个工频周期，相较于现有励磁涌流快速识别算法时间较长，但由于算法逻辑是在启动后首先闭锁差动保护，判断为励磁涌流则继续闭锁，不会对保护产生影响。

4.3 和应涌流

一台变压器空载合闸时，与其并列运行的变压器上会产生和应涌流，其幅值较励磁涌流小且先增大后减小，产生时间会相对滞后，给差动保护带来一定的挑战。变压器T2 正常运行，T1 空载合闸以模拟和应涌流，判据1 的三相输出结果δ1/S1分别为446.7/1、0/0、454.4/1，判据2 的三相输出结果δ2/S2分别为347.0/1、0/0、335.4/1，保护可靠闭锁。A 相计算结果见附录B 图B3。第1 个工频周期，保护启动条件不满足；第2 个工频周期，和应涌流幅值逐渐增大，保护启动，但此时达不到算法启动的条件，闭锁半个周期后解除闭锁，由于差动电流小于整定值，保护也不会误动；第3 个工频周期，保护启动，算法也启动，可靠地闭锁了差动保护。可见，本文所提算法对和应涌流也可正确识别。

4.4 考虑TA 饱和的内部故障

故障发生之初，由于故障发生时刻不同，故障电流中会包含不同程度的直流分量，可能会引起TA饱和，这是以往很多研究中未考虑的一点。考虑TA 饱和下内部故障的故障电流波形会发生畸变，可能会对励磁涌流的识别产生影响，为此，对TA 饱和时的两相及三相短路进行仿真，饱和最严重的三相短路的算法计算结果如表2 所示。

表2 TA 饱和时三相短路的计算结果Table 2 Calculation results of three phase short circuit with TA saturation

由仿真结果可以看出，内部故障发生TA 饱和时，所提方法仍可以正确识别，一些情况下通过判据1 即可正确识别，部分故障时刻需要判据2 开放误闭锁的故障电流，TA 严重饱和时，亦可以正确开放保护，判据计算结果均与整定值有较大差距，算法可靠且有较强的抗饱和能力。0°合闸角下AB 两相接地短路时A 相差动电流的计算结果见附录B 图B4。从波形来看，内部故障时发生TA 饱和会使电流波形的基波相似性变差，文献［21，26］等单纯与正弦特征比较的算法会误判为励磁涌流将保护闭锁。虽然与文献［29］等1 个工频周期识别的算法相比，本文算法会多出部分数据短窗的采样时间，但判据2增加的计算量极小。

4.5 考虑TA 饱和的励磁涌流

同样的，励磁涌流中也含有大量非周期分量，极易发生TA 饱和，对考虑TA 饱和的励磁涌流进行仿真，计算结果如表3 所示。

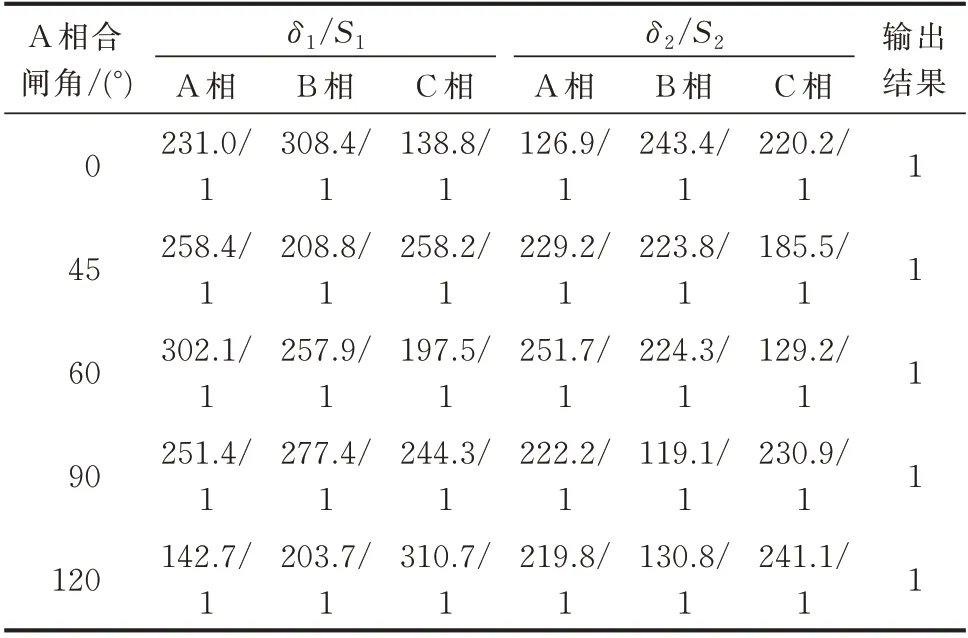
表3 TA 饱和时励磁涌流的计算结果Table 3 Calculation results of inrush current with TA saturation

考虑TA 饱和，0°合闸角时A 相励磁涌流的计算结果见附录B 图B5，可以看出，涌流饱和后，间断角特性减弱，会对传统间断角原理的识别方法产生影响，但其基波相似性仍然很差，本文算法仍然可靠闭锁。

4.6 空合于内部轻微匝间故障

空载合闸于内部轻微匝间故障的情况也常被忽略，轻微故障时励磁涌流特征占主导，一些现有的方法会将其误判为励磁涌流，闭锁保护，导致故障进一步扩大。本文算法的结果如表4 所示。

表4 空合于内部轻微匝间故障时计算结果Table 4 Calculation results of no-load closing with slight internal turn-to-turn fault

空载合闸于内部1.5%匝间故障时A 相差动电流见附录B 图B6，对空载合闸于内部轻微的匝间故障，本文算法利用其差动电流特征，选择能够正确反映故障信息的位置，实现此类情况的正确识别并开放保护。而对于文献［29］，前半个工频周期涌流的存在会使算法误判，其他一些分析波形特性的算法也会因故障电流和励磁涌流的同时存在而产生误判。

4.7 考虑变压器不同电压等级及接线方式

为了验证本文算法的可靠性，在PSCAD 中搭建了含有一台容量为630 kVA、变比为10 kV/0.4 kV，Dyn11 接线变压器的配电系统，采用双交流源模拟剩磁［34］，其余设置及整定值均不变，仿真了故障及涌流的各种情况。限于篇幅，仅列出了部分结果，见附录B 表B3。对于仿真的各种故障情况，算法均可以正确反应。由此可见，本文算法及所给整定值从波形基波相似性出发，可以适用于不同电压等级以及不同接线方式的变压器差动保护，都能实现内部故障的快速开放及励磁涌流的可靠闭锁，且在TA饱和、空合于内部轻微匝间故障等特殊情况下也都能保证可靠性。