三相不平衡高频振荡的相量测量方法

陈 垒，谢小荣，于光远，尹爱辉

（1. 清华大学电机工程与应用电子技术系，北京市 100084；2. 国网山东省电力公司济南供电公司，山东省济南市 250000）

0 引言

近年来，中国电力系统发生了多次高频振荡事件。例如：2017 年鲁西背靠背柔性直流输电工程出现了1 270 Hz 左右的高频振荡现象，导致换流器跳闸［1］；2018 年渝鄂柔性直流输电工程在调试期间分别出现了700 Hz 和1 810 Hz 的振荡［2］。这种高频振荡一旦发生，将会严重危害电力系统安全稳定运行。目前，中国海上风电多采用柔性直流输电系统送出，因此，高频振荡风险不可避免。

为了让系统调度员实时了解振荡的频率和幅值信息，并针对性地采取振荡抑制措施，需要实现高频振荡相量和频率的实时准确测量。基于巨磁阻效应的电流传感器在大量程、宽频带范围内均有良好的性能［3-4］，且相应的测量方法可依托相量测量单元（phasor measurement unit，PMU）实现。这些均为在柔性直流输电系统中准确测量高频振荡相量提供了基础。

通过分析现场数据发现，柔性直流系统中发生的高频振荡一般具有三相不平衡特征。这主要是由于系统在振荡频率处正负序均存在不稳定模式，系统扰动后同时引发正序振荡和负序振荡，造成三相不平衡［5］。

由文献［6］可知，负序振荡分量会对正序相量测量造成干扰，从而导致高频振荡相量测量存在误差。因此，在测量正序相量时，测量方法应具备负序分量干扰的抑制能力。而目前已有的振荡相量测量方法主要关注三相平衡下正序振荡相量的测量问题，少有关注振荡三相不平衡下负序分量干扰的抑制问题。

文献［7-8］提出了基于Prony 和Adaline 等现代谱估计理论的低频振荡参数测量方法。针对电力系统次同步振荡参数测量，文献［9］对目前已有的方法进行了综述。目前文献中的次同步振荡检测方法主要包括2 类。一类是基于PMU 同步基波相量测量数据的检测方法［9-10］，其一般假设PMU 采用的相量测量方法为离散傅里叶变换（discrete Fourier transform，DFT），然后推导次同步振荡参数与基波相量测量结果之间的关系。这一类方法并不适用高频振荡相量测量。这主要是由于PMU 最高数据上传速率仅为100 帧/s。根据香农采样定理，如此低频率的数据不包含高频振荡信息，因此不能从PMU测量得到的基波相量数据中恢复高频振荡相量等信息。另一类是基于电网电压电流采样信号的测量方法［11-13］。例如，文献［12］提出先用平均滤波方法滤除基波和谐波分量，再采用DFT 计算次同步振荡幅值和相位等参数。基于该方法计算正序振荡相量时，须首先计算各相的振荡相量，然后采用对称分量法计算正序相量。然而，当三相振荡分量不平衡时，镜像振荡频率分量对各相振荡相量测量结果的影响不同，也就导致计算得到的正序振荡相量中含有负序分量干扰，因此存在误差。文献［13-14］中的方法也存在该问题。另外，文献［15］提出的基于子空间的电力系统振荡相量测量算法考虑了不超过300 Hz 的中频振荡参数测量问题。文献［16］讨论了宽频带相量测量框架，并提出用DFT 测量宽频带相量。但这些方法都未考虑三相振荡信号不平衡情况下的高频振荡相量测量问题。

本文针对上述问题，提出基于sinc 插值函数的正序高频振荡相量测量方法，能有效抑制负序振荡分量的干扰，并通过仿真实验和实测数据验证了所提方法的有效性。

1 高频振荡相量测量方法

1.1 高频振荡三相电流信号

含有基波和振荡间谐波分量的三相电流信号sp(n)（p=A，B，C）可以表示为：

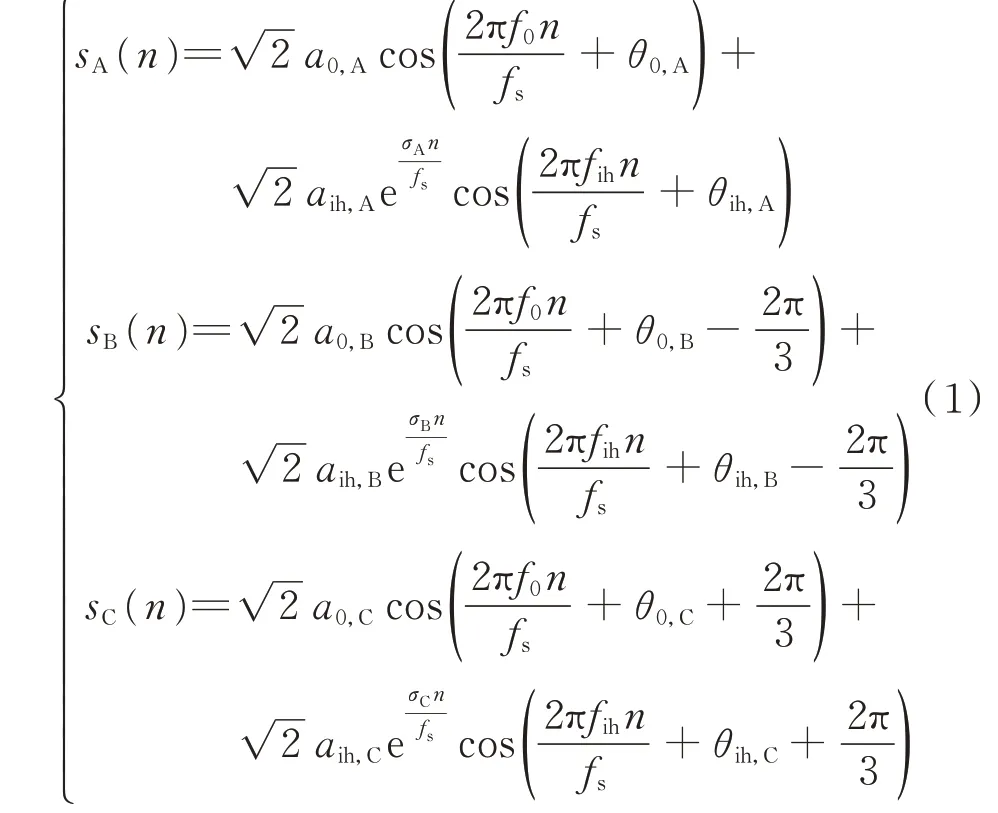
式中：f0、fih、fs分别为额定频率、间谐波频率和信号采样频率；a0，p和θ0，p分别为p相基波有效值和相位；aih，p和θih，p分别为p相间谐波初始有效值和相位；σp为p相间谐波幅值的衰减因子；n为采样点编号。

根据上文所述，三相高频振荡分量可以是不平衡的，即三相的幅值aih，p、衰减因子σp和相位θih，p可以不相等。图1 给出了国内发生的某高频振荡事件中三相电压电流波形，可以发现上述波形中有明显的三相不平衡特征。

图1 某高频振荡事件中三相电压、电流波形Fig.1 Three-phase voltage and current waveforms in a high-frequency oscillation event

1.2 三相信号的Clark 变换

对式（1）所示三相信号进行Clark 变换，并进行推导后得到变换后的信号波形Cα，β(n)。

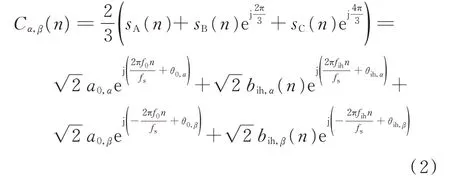
式中：下标α和β分别表示正序和负序分量；bih，α(n)和bih，β(n)分别为信号变换后的正序和负序振荡分量有效值。从式（2）可以看到，当三相高频振荡信号不平衡时，bih，β(n) ≠0，而这部分负序分量会给正序振荡相量的测量带来干扰。

为了抑制负序分量干扰，本文的思路是在信号模型中加入负序分量，即可在实现正序振荡相量测量的同时实现负序分量的陷波处理。但振荡幅值是一个时变量，因此，还需要用参数化模型对正负序分量进行建模，从而描述振荡信号的时变特征。

1.3 振荡相量建模

正负序振荡相量一般可视作一个基带带限信号。那么，在很窄的时间窗n∈[-N2 +1，N2 ]内，该带限信号可以近似地表示为若干个sinc 插值函数的线性叠加［16-17］，其中N为时间窗长度。以正序振荡相量建模为例，可以将其表示为：

式中：pih，α(n) =bih，α(n)ejθih，α为高频振荡正序相量，即为待测量的相量值；B为一个不小于基带信号pih，α(n)最高频率的频率值（B≠0），2B为该带限信号的采样频率；pk，α=pih，α(k2B)为pih，α(n)在n=kfs/(2B)时刻的采样值；k为采样点编号；2K为用于重构振荡相量信号的采样点数，因此，2K可以被视为模型阶数。另外，时间窗长度Tw一般应满足Tw＜k/B。需要说明的是，传统的信号建模方式一般针对稳态信号，而本文建模方式可准确描述频谱在一定范围内分布的时变信号［16-17］。

1.4 振荡频率和正序相量测算

在实现振荡相量建模后，就可以实现式（2）中信号的近似表示。对该近似表示的电网信号进行DFT 计算可以得到频谱分析结果S(c)：

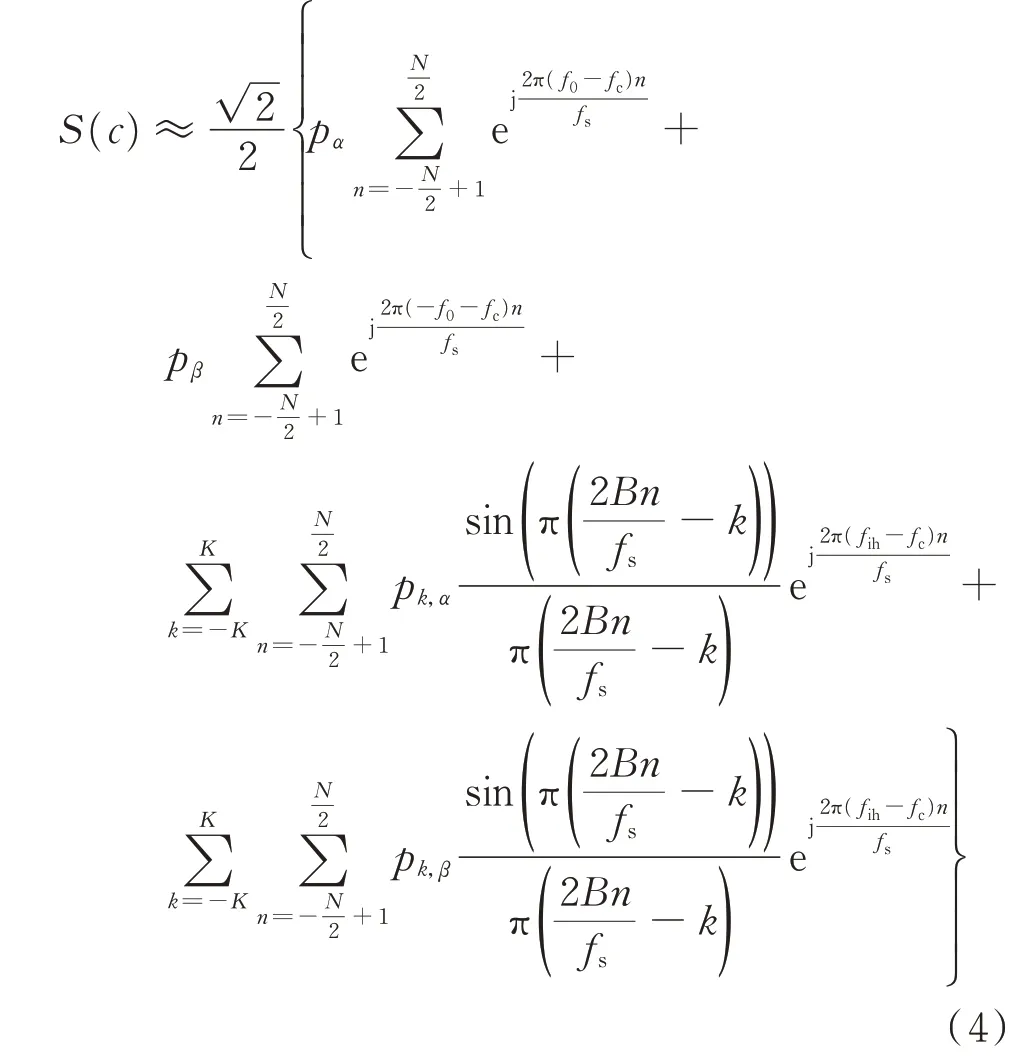
式中：pα=a0，αejθ0，α和pβ=a0，βejθ0，β分别为正、负序基波相量；pk，β=pih，β(k/2B)为pih，β(n)在n=kfs/(2B)时刻的采样值；fc=cfs/N为DFT 计算的频率，其中c为DFT 计算的谱线序号。可用振荡频率附近幅值最大的若干根谱线信息进行pk，α的测算，fc即为这些谱线对应的频率。N取每周期采样点数的整数倍。如此，基波和可能存在的低次谐波在高频振荡频率附近的若干根谱线对应DFT 的变换值为0，从而可有效避免基波和可能存在的谐波对振荡频率附近的频谱值产生影响。为了减小计算负荷，同时提高正序振荡相量测量的响应速度，本文将N取为一个基波周期长。因此，在忽略式（4）中基波分量的DFT值后，其可表示为如下矩阵形式。

式中：Sα和Sβ分别为包含2K+1 个电网电流信号DFT 计算值的正、负序列向量，用于计算它们的DFT 频率fc分别为振荡频率和负振荡频率附近幅值最大的谱线对应的频率；z为每一行包含了2K+1个sinc 插值函数DFT 的变换值；上标*表示共轭算子；pα和pβ分别为包含了pk，α和pk，β的列向量；V为包含了z和z*的矩阵；X为包含了Sα和Sβ的列向量；R为包含了pα和pβ的列向量。

为了抑制负序分量对正序振荡相量测量带来的影响，式（5）中包含了负序分量部分的计算结果，如此，负序分量也包含在信号模型中。因此，在通过式（5）计算正序振荡相量时，负序分量的影响得到了抑制，即从滤波器的角度考虑，可认为实现了负序分量的陷波处理［18］。列向量R可通过式（6）进行测算。

在对式（2）所示信号进行近似表示时，fih是未知的。本文基于插值DFT 初步估计fih，记为f^ih。其计算原理和方法较为成熟，本文不再赘述，具体可参考文献［14］。因此，根据式（3），正序振荡相量在0 时刻的m阶导数可以基于pk，α的估计值p^k，α进行测算，即

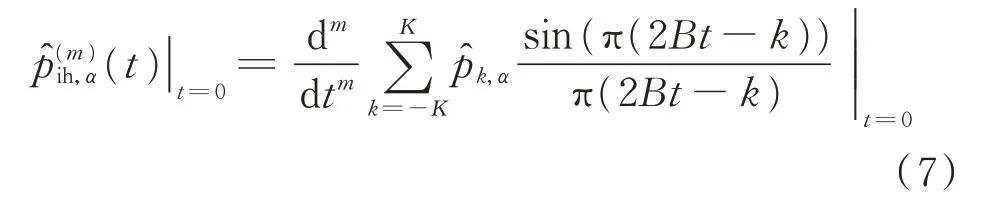
式中：Im {·}表示相量虚部算子。

2 计算流程和计算量分析对比

本文方法通过如下步骤完成：①基于式（2）计算三相信号的Clark 变换信号；②基于插值DFT 粗略估计高频振荡频率；③基于式（4）计算Sα和Sβ；④基于式（6）测算pk，α和pk，β；⑤基于式（8）和式（9）计算高频振荡相量和频率。

由于计算相量导数和频率仅需几次加减和乘除，因此第⑤步的计算量基本可忽略不计。第①步中需要3(N-1)次加法和4N次乘法；第②步和第③步共需要进行4K+2+N次DFT 计算（这里的DFT 计算是指计算每个频谱值所需的计算量）；第④步中需要对4K+2 阶方阵进行求逆运算。由于本文K取1，因此待求逆方阵的阶数仅为6 阶。另外，由于时间窗长度仅为20 ms，因此即使当PMU采样率为12.8 kHz 时，以上计算量总和也不超过10 000 次浮点运算。

采用目前最常用的插值DFT 算法［16］计算正序振荡相量时，首先需要对三相信号进行Clark 变换，然后对变换后的信号进行加窗DFT 运算，最后通过插值估计高频振荡频率和高频振荡相量。相对于本文所提算法，插值DFT 方法不需要进行上述步骤③至⑤中的计算，计算负荷明显减小。

一般而言，为进一步提高准确度，须将上述插值DFT 算法估计得到的高频振荡频率作为式（3）信号模型中的初始频率值，并进一步在频域将信号模型与实际信号进行比较，估计得到高频相量和频率值。具体原理与本文方法类似，唯一的区别是式（5）中不包括负序高频振荡分量对应的计算值，即Sβ，而计算步骤与本文方法相同。与本文方法相比，该算法在第②步和第③步中仅需进行2K+1+N次DFT 计算；第④步中需要对2K+1 阶方阵进行求逆运算。因此，该算法的总计算量也小于本文算法。

然而，由于每次执行本文算法所需的浮点运算数不超过10 000 次，而目前常用的数字信号处理器每秒能进行上亿次浮点运算。因此，完全能够完成本文算法计算。

3 算法性能测试

本章通过仿真实验分析所提高频振荡相量测量方法的性能。首先，采用数值仿真信号评价振荡频率取值和电流存在谐波对所提振荡检测方法性能的影响；然后，采用典型柔性直流输电系统中出现的高频振荡PSCAD 仿真信号验证所提振荡相量测量方法的性能；最后，采用国内发生的高频振荡录波数据测试所提出方法的性能。

为了展示本文方法对负序分量干扰的抑制性能，与未考虑负序分量干扰的振荡相量测量方法进行比较。插值DFT 算法是一种常用的高频振荡相量测量方法［16］，但由于该方法不存在迭代环节，因此准确度比本文方法低。为了公平地进行比较，在插值DFT 算法的基础上增加类似本文的迭代环节，区别在于式（5）中不包含负序分量部分，下文将该方法称为传统方法。实验中电网信号的采样率为10 kHz，正/负序振荡相量建模参数B取2.5 Hz，采用振荡频率和负振荡频率附近3 根幅值最大的谱线信息进行振荡相量测算，并用IEEE/IEC 标准［19］中定义的综合矢量误差（total vector error，TVE）和频率误差评价2 种方法的性能。

3.1 振荡频率的影响

不同振荡模式下振荡频率可能不同，本节考察振荡频率对所提出方法性能的影响。采用式（10）中的信号sp(t)进行分析。在各个子实验中，fih以20 Hz的步长从500 Hz 递增到2 500 Hz。衰减因子σ为1，A 相初始振荡幅值a为0.2，基波频率f为50 Hz。

附录A 图A1 展示了高频振荡频率为540 Hz 时本文方法的中间结果，包括Clark 变换信号的频谱分析结果（见图A1（a））及插值DFT 估计得到的高频振荡频率值（见图A1（b））。从图A1（a）可以看出，三相不平衡信号中含有明显的负序分量。从图A1（b）可以看出，插值DFT 估计得到的频率误差较大，需进一步通过迭代运算提高准确度。

图2 和图3 分别展示了不同振荡频率下本文方法和传统方法对应的TVE 和频率误差。可以发现，即使振荡频率不同，本文所提出的方法的TVE 和频率误差均很小，如TVE 总小于0.002%，频率误差总小于0.002 Hz。而且，本文所提出的方法的准确度要明显高于传统方法。对振荡频率测算而言，本文方法将传统方法近0.22 Hz 的误差减小为0.002 Hz。这说明本文方法对负序分量干扰起到了很好的抑制作用。

图2 不同振荡频率下2 种方法对应的TVEFig.2 TVE corresponding to two methods with different oscillation frequencies

图3 不同振荡频率下2 种方法对应的频率误差Fig.3 Frequency errors corresponding to two methods with different oscillation frequencies

3.2 不平衡程度的影响

不同振荡事件中，三相振荡分量的不平衡程度可能不同。本节通过不断调节式（10）中A 相信号的振荡幅值来改变不平衡程度，以测试本文方法和传统方法的性能。具体而言，在10 次测试中，参数a的值以0.1 的步长逐渐从0.1 变化到1，而A 相的初相位总是0°，振荡频率为520 Hz。

附录A 图A2 和图A3 分别展示了不同不平衡程度下本文方法和传统方法对应的TVE 和频率误差。可以看到，当a值为0.1、相位为0°，即三相振荡分量平衡时，本文方法与传统方法的TVE 及频率误差均相同。而随着不平衡程度的增加，传统方法的TVE 及频率误差快速增加。相较而言，本文方法的TVE 及频率误差基本维持不变。这主要是由于本文方法有效抑制了负序分量干扰。

3.3 次同步间谐波干扰的影响

在高频振荡发生过程中，由于干扰影响，信号中还可能存在次同步间谐波分量。本节分析该分量对高频振荡相量测量的影响。在9 次测试中，次同步间谐波的频率以5 Hz 的步长逐渐从5 Hz 变化到45 Hz，幅值为基波幅值的1%，相位与基波相位相同，高频振荡频率为520 Hz。

附录A 图A4 和图A5 分别展示了次同步间谐波频率不同时本文方法和传统方法对应的TVE 和频率误差。可以看到，当信号中存在次同步间谐波分量时，本文方法的TVE 和频率误差均增大。TVE 值最高约达0.8%，频率误差最高约达0.08 Hz。然而，即使在次同步间谐波干扰的情况下，本文方法的准确度仍要高于传统方法。

3.4 谐波干扰的影响

电网信号中不可避免地会存在谐波分量。本节根据IEEE/IEC 标准［19］测试谐波对所提方法性能的影响。一般而言，电网中较低次谐波含量更为丰富。本节主要测试信号中含有第2 至7 次谐波分量时方法的性能。具体地，在式（10）中增加一个谐波水平为1%的谐波分量。为了测试所提出方法可能受到的最大影响，振荡频率应尽量靠近谐波，为此将振荡频率设定为520 Hz。

附录A 图A6 和图A7 分别展示了不同次数谐波干扰下2 种方法对应的TVE 和频率误差。可以看到，即使受到谐波干扰，2 种方法的准确度基本不变。这主要是由于本文采用基于DFT 的频域插值的方法测算振荡相量值，而DFT 能很好地抑制谐波分量对振荡频率附近频谱的干扰，因此谐波干扰基本不影响高频振荡相量的测量准确度。

3.5 振荡频率时变的影响

由于系统拓扑或其他参数变化，高频振荡频率也可能是时变的。为了测试这种情况的影响，本节考虑振荡频率在520～521 Hz 范围内线性变化。其他参数与式（10）一致，即振荡幅值也存在时变。

附录A 图A8 和图A9 分别给出了振荡频率线性变化下2 种方法对应的TVE 和频率误差。可以看到，本文方法对应的最大TVE 及频率误差分别为0.002%、0.01 Hz；而传统方法对应的最大TVE及频率误差分别为0.74%、0.24 Hz。因此，本文方法仍明显比传统方法准确。

3.6 典型柔性直流输电系统高频振荡仿真信号

本节以典型柔性直流输电系统为例，通过PSCAD 时域仿真获取高频振荡电流信号验证所提出方法的性能。本文所考虑的典型柔性直流输电系统的拓扑结构如附录A 图A10 所示［5］。由图A10 可见，当变电站间的输电线由于检修或其他原因断开后，系统中出现了高频振荡线性。

附录A 图A11 展示了振荡发生前后测量点处的三相电流波形及振荡发生后的电流信号频谱（时间窗长度为1 s）。从三相电流波形图可以看出，该高频振荡具有明显的三相不平衡特征。从频谱图可以看出，系统发生了约1 272 Hz 的振荡。

图4 和附录A 图A12 分别展示了本文方法和传统方法测算得到的振荡频率和正序振荡幅值。可以发现测量结果与附录A 图A11 中的频谱分析结果相近。由于实际振荡频率和正序振荡相量未知，所以无法计算振荡频率误差和TVE。但由于高频振荡发生后系统参数并未发生改变，因此可认为振荡频率一直不变。如此，可以通过分析频率值的波动程度判断测量方法的精度。通过计算得到，传统方法距离平均值的最大偏差为0.50 Hz，而本文方法仅为0.38 Hz。在如附录A 图A12 所示的2.5～2.6 s 范围内，可认为二次拟合后得到的振荡幅值曲线为振荡幅值真实值。本文方法与真实值之间的最大偏差为0.47 A，而传统方法为0.57 A。根据上述分析，可知本文方法比传统方法有更高的精度。

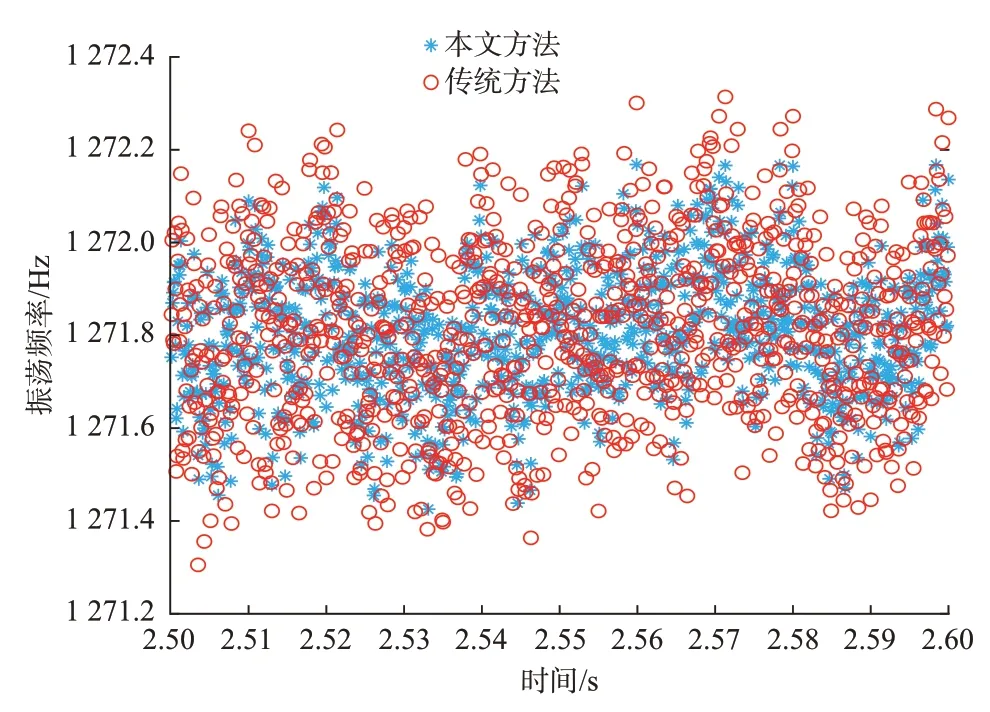
图4 2 种方法的振荡频率测算值Fig.4 Measured values of oscillation frequency for two methods

4 高频振荡事件实测数据

分别对图1 所示的国内某高频振荡事件实测电压、电流数据进行分析处理，得到了如图5 所示的振荡频率的测算值。通过比较本文方法和传统方法测量结果发现，本文方法最大偏离平均值为0.4 Hz，而传统方法最大偏离平均值为0.65 Hz。因此，可以得出本文方法比传统方法精度更高的结论。

图5 基于电压实测数据计算的振荡频率Fig.5 Calculated oscillation frequencies based on voltage measured data

5 结语

本文针对高频振荡三相信号不平衡问题，提出了一种基于sinc 插值函数的高频振荡相量测量方法。首先，对三相信号进行Clark 变换；然后，基于sinc 插值函数对正序和负序分量进行参数化建模；最后，通过求逆运算得到模型参数，并进一步计算得到正序振荡相量和振荡频率。本文通过sinc 插值函数对负序分量进行建模，实现了负序分量干扰的有效抑制。通过数值仿真实验、PSCAD 仿真数据实验和实测数据实验发现，本文方法的频率误差总小于0.08 Hz，TVE 总小于0.8%；而且本文方法比传统方法更能抑制因三相不平衡引入的负序分量干扰，具有更高的振荡相量测量准确度。另外，本文方法还具有计算量低的特点，工程应用潜力大。

但是，本文尚未在实际工程中验证所提方法的性能。下一步将考虑研制高频振荡相量测量装置，并将其应用于工程实践中。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。