基于MATLAB的五轴坡口切割机器人运动学分析与仿真

张雪健, 胡晓兵, 蒋从军, 毛业兵

(1.四川大学机械工程学院, 成都 610065;2.宜宾四川大学产业技术研究院, 宜宾 644600；3.中国水电建设集团夹江水工机械有限公司, 乐山 614100)

工业机器人和人工智能技术,作为第三次和第四次工业革命的中坚力量,其发展对于一个国家的制造业发展起着至关重要的作用[1].目前,工业机器人广泛应用于上下料、焊接、码垛等机械作业.在焊接作业的智能化和自动化改造中,坡口切割的自动化逐渐成为了一个发展的热点.但国内目前还没有成熟的完全自主研发的坡口切割机器人.许多企业和高校都在这方面进行着努力和尝试,并且许多团队已经有了一定程度上的技术上的突破[2].目前,国内的坡口切割机器人的研究主要集中在三个方面,机器人视觉系统的研究,机器人控制系统的搭建和针对不同零件的焊接工艺研究.在机器人视觉系统的研究中,国内高校和企业已有针对视觉技术进行了多方面的研究.例如哈尔滨工程大学的团队根据机器人模型,对图像拼接、轮廓提取进行了研究,然后根据归一化链码直方图提出了一种新的轮廓匹配方法[3].北京石油化工学院的团队对于复杂工况下机器人视觉引导系统的二维图像拼接和三维点云拼接进行了研究.在机器人控制系统搭建的研究中[4],哈尔滨工程大学研发了一台基于工业CCD和工业结构光的五轴坡口切割机床[5].文献[6]根据OTC AX-MV6机器人的机械结构和生产需求设计了一个坡口切割工作站的控制系统.在坡口机器人焊接工艺的研究中,哈尔滨理工大学的团队针对于管状零件的相贯线坡口切割原理和零件的切割作业运动学仿真进行了研究[7].而梁卫等则是对于桁架臂相贯线坡口焊接进行了深入的研究[8].

在以上三个研究方向中,机器人控制系统的搭建和机械本体的运动学分析等相关研究相较于视觉系统和工艺研究相对较少,因此为了改变坡口切割作业的生产加工方式,本文设计了一种基于机器视觉的五轴坡口切割机器人.其可以根据视觉系统,获取零件尺寸和加工要求并生成零件加工轮廓[9],然后根据零件轮廓信息,生成机器人的末端操作器轨迹,进而操作机器人完成坡口切割作业.为验证设计的可行性,对五轴坡口切割机器人进行运动学分析.机器人的运动学分析[10-12]不仅是机器人动力学分析的基础,对于机器人运动空间、运动控制和轨迹规划等问题的研究也提供了依据.机器人的运动学分析主要对机器人进行正逆运动学分析,然后借助MATLAB软件对机器人进行运动学建模,然后对机器人末端操作器的运动空间和末端轨迹进行仿真验证.

本文的设计方案和实验仿真主要有如下三个：(1) 机械结构的设计的创新性.本文设计的坡口切割机器人为五轴直角坐标式机器人下相较于传统机器人有三个优点：① 结构简单且运动学分析和动力学分析相对简便；② 机器人的重复定位精度高；③ 控制方案相对简便,本文设计的机器人为五轴四联动式,即只有一个回转关节和三个移动关节联动.(2) 综合MATLAB软件相关功能和一些常用的仿真分析算法,为机器人进行不同方面的仿真分析,进而对坡口切割机器人进行可行性和合理性分析.(3) 采用MATLAB仿真图的方式去验证机械结构设计的合理性,包括通过采用MATLAB机器人工具箱,对机器人的机械结构进行仿真建模,验证其是否满足设计需求.

2 机器人结构设计

在平板坡口切割作业过程中,为满足机器人在三维工作空间内对于零件的加工,首先需要对零件的加工位置进行准确定位,然后再根据切割要求控制焊枪的姿态,进而才可进行切割作业.本文设计的坡口切割机器人系统包括机械本体和控制系统两部分构成.其中机械本体由X,Y,Z,U,V这5个运动关节和相应的电机构成.控制系统包括由图像采集模块、工程图读取模块、图像处理模块、轨迹计算模块、通讯模块和运动控制模块构成的上位机模块、由PLC控制单元和电路模块构成的下位机模块和工业相机三部分构成,如图1所示.

在定位过程中,由于零件的尺寸不同,形状多样,厚度不一,因此采用X,Y,Z三轴的空间直角坐标结构对零件进行准确的三维空间定位.此外由于零件尺寸不同且坡口切割角度不同,采用传统的垂直向下的火焰枪结构无法满足多样化的坡口切割作业要求,因此采用两个回转关节实现对末端火焰枪的位姿控制.其中一个回转关节用于固定焊枪位置,保证其在切割过程中始终与零件轮廓相垂直；另一个回转关节则依据坡口切割角度控制焊枪姿态使其满足不同的切割作业要求.机器人的机械本体如图2所示,采用直角坐标形式[13],其中，X,Y,Z为移动关节，U,V为回转关节.整体机器人采用串联驱动结构,直线移动关节X,Y,Z可由关节驱动电机带动丝杆沿各自导轨滑动,回转关节U和V可由关节驱动电机带动,分别实现沿末端操作器Z轴方向的360°回转运动和X轴方向的90°摆动运动.

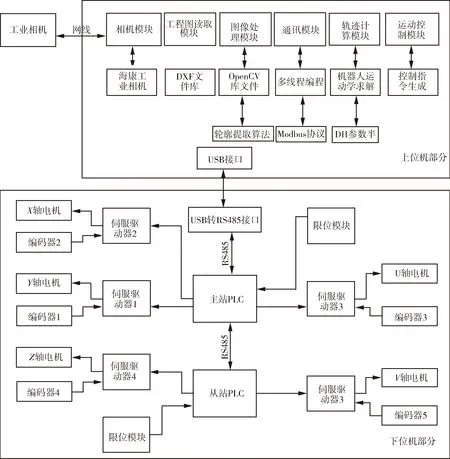
图1 机器人控制系统图Fig.1 Control system scheme of five axis groove cutting robot

2.2 机器人末端操作器位姿设计

坡口切割机器人一般应用于平板类零件的坡口切割.因坡口切割零件的尺寸不同、坡口切割角度不同,末端火焰枪也需要根据不同的作业要求进

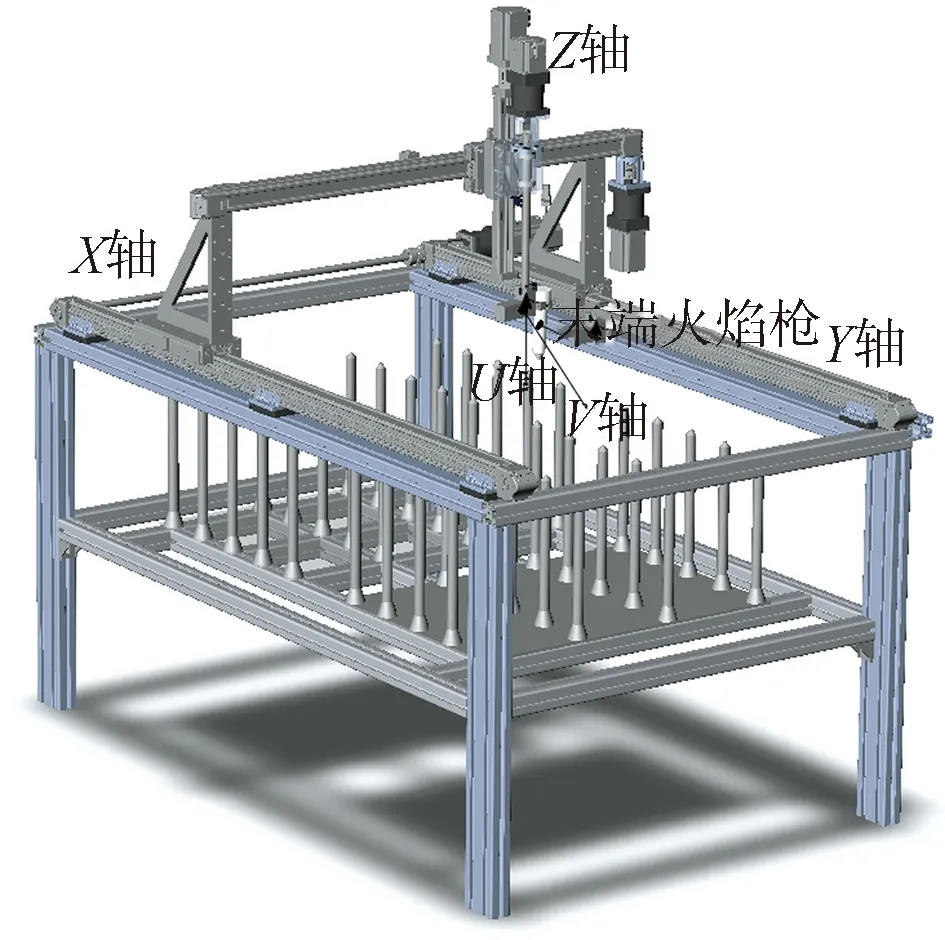
图2 机器人实验台模型

行调整.切割作业过程中必须保证火焰枪时刻与零件轮廓相垂直,坡口切割形状由末端火焰枪姿态决定.如图3所示,末端火焰枪在零件平面的投影需要与零件当前轨迹位置相切,即与当前位置的法线重合.

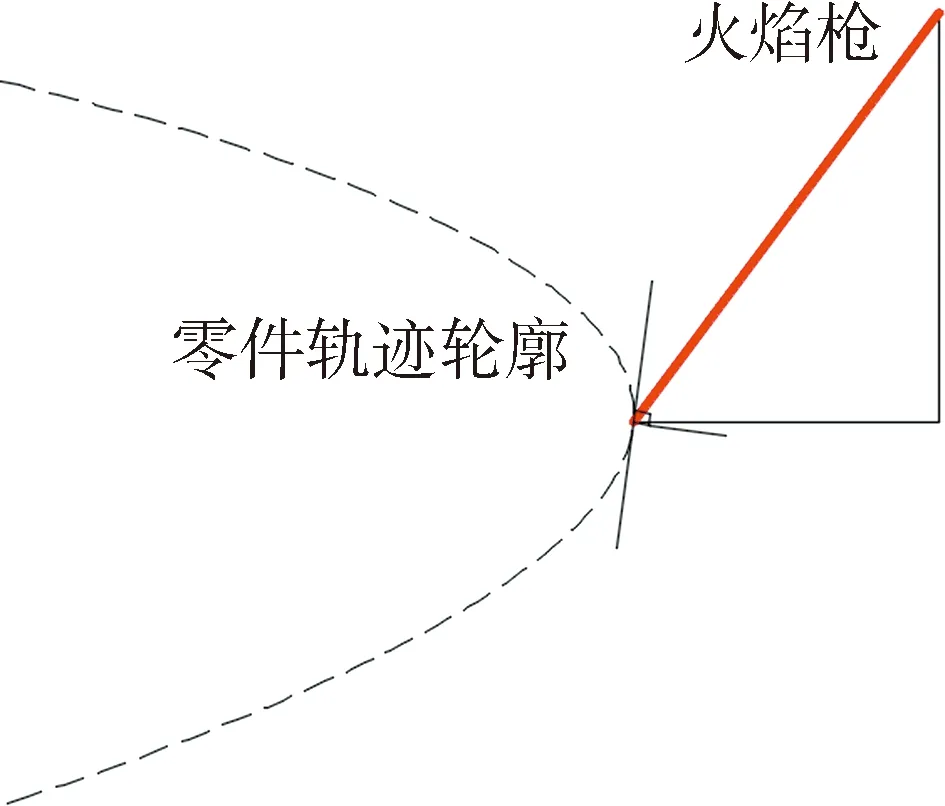
图3 机器人末端火焰枪与零件轮廓姿态关系图

3 机器人运动学分析

对坡口切割机器人的运动学分析主要分为对各运动轴的正逆运动学分析和对机器人末端火焰枪的运动与位姿分析.

3.1 机器人正运动学分析

五轴坡口切割机器人的正运动学分析,首先根据机器人机械本体模型图求出机器人的DH参数表,画出机器人D-H坐标简图,然后根据DH参数表获取关节变换矩阵.准确描述机器人位置和姿态是对机器人进行运动分析的基础,本文采用改进的DH参数法[14],对机器人机械本体模型进行简化,建立空间直角形串联机器人的DH坐标简图(图4),然后根据对机械本体的测量和计算,得到五轴坡口切割机器人的DH参数表(表1).

表1 机器人DH参数表

表1中,θi为轴Xi-1和Xi之间的夹角;di为Oi′沿Zi-1的坐标;ai为Oi′和Oi之间的距离;αi为轴Xi-1和Xi之间的夹角.为了简化计算,将世界坐标系与基坐标系重合,设为O0-X0Y0Z0.对DH参数表需要说明,因机器人Y轴与X轴不是在同一水平面内,因此以连杆2的a2的数值来近似处理.此外,通过对于机械本体的实际测量,对机器人DH参数进行一定的补偿,即offset栏.

图4 机器人DH坐标简图Fig.4 DH coordinate sketch of robot

(1)

相邻两个关节的转换矩阵满足关系式(2).

(2)

因此,可以推出由基坐标系到末端操作器坐标系之间的坐标转换矩阵为

(3)

nx=-cosθ4sinθ5

ny=sinθ4sinθ5

nz=-cosθ5

ox=-sinθ4

oy=cosθ4

oz=0

ax=cosθ4cosθ5

ay=sinθ4cosθ5

az=-sinθ5

dx=d1-46.5sinθ4-100cosθ4sinθ5-320.3

dy=46.5cosθ4-d2-100sinθ4sinθ5

dz=d3-100cosθ5-191.1

(4)

即可得五轴坡口切割机器人末端操作器位姿矩阵：

(5)

3.2 机器人逆运动学分析

θ4=u-π/2

(6)

θ5=v

(7)

求得θ4和θ5表达式后,带回式(4)中,可得出d1,d2,d3,即

3.3 坡口机器人末端火焰枪分析

对机器人的末端火焰枪的运动学分析主要分为角度分析和距离分析两部分.(1) 角度分析.由于本文设计的坡口切割机器人只针对于平板类零件的切割,即只会存在一维的末端火焰枪位姿变化,因此末端火焰枪的位姿可以通过初始设定保证.为了简化机器人运动方案,本文设计的机器人为五轴四联动式机器人,即有一轴不参加机器人的联动运动,控制末端火焰枪位姿的V轴不随末端火焰枪的移动而移动,时刻保证末端火焰枪与待切割零件夹角为v.在一般的批量加工过程中,坡口切割角度设置为45°即可.(2) 距离分析.火焰枪与代加工零件之间的距离会影响末端火焰枪的焊缝补偿、预热时间、氧气压力、乙炔压力等切割参数.由于本文设计的坡口切割机器人只针对于平板类零件的切割,因此对坡口切割机器人末端火焰枪而言,它与代加工零件加工表面的距离是一定的.因此,我们可以将这个定值距离在机器人结构分析中进行补偿,即将其设置为机器人的固定参数,从而不需要对其进行实时设定.

3.4 坡口机器人轨迹规划分析

考虑到本文只针对于平板类零件的坡口切割,因此本文设计的坡口切割机器人不需要考虑三维运动学轨迹分析,其运动轨迹完全可以由轨迹点进行二维量化.机器人轨迹规划的轨迹插值方案只需要采用五次多项式插值进行二维插值运算.对于某种代加工零件需要进行两段不同切割方案,不需要考虑轨迹过渡.因为坡口切割一般为焊接的前置工艺,对于平板类零件而言,其焊接表面均为平面,不存在三维曲面.因此,不同的切割轨迹不需要考虑过渡轨迹,可以按照两部分切割进行.此外,平面类零件的坡口切割末端火焰枪的运动只由两个维度的运动合成而来,因此切割速度的控制可以通过速度分解.将其分解为平面两个轴的速度,进而可以通过两个关节处关节电机的驱动来控制机器人的速度.

4 机器人MATLAB运动学仿真

4.1 机器人运动模型仿真

由上述机器人正逆运动学分析,利用MATLAB软件的机器人工具箱建立五轴坡口切割机器人的仿真模型[15].利用此仿真模型,可以进行机器人轨迹控制算法的设计和对正逆运动学的验证.

由表1的机器人DH参数,利用MATLAB机器人工具箱中的Link、SerialLink、fkine等函数,获得机器人的运动学仿真模型[16](如图5).

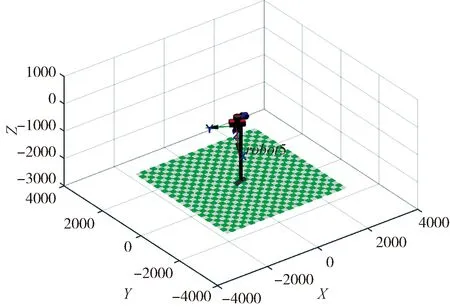
图5 机器人运动学模型简图Fig.5 Sketch of robot kinematics model

4.2 机器人末端操作器工作空间仿真

五轴坡口切割机器人的坡口切割作业有一定的工作空间要求,因此需要对坡口切割机器人进行工作空间仿真[17-18]以确定可以由机器人进行切割加工零件的尺寸范围.本文采用蒙特卡洛随机数算法对末端火焰枪运动空间，即末端操作器工作空间求解.该算法是一种通过随机概率来解决问题的数值方法,可以实现运动空间的数字化近似,常用于多关节机器人工作空间的求解.

本文利用MATLAB软件进行编程,设置随机数量为N=10 000,然后获得机器人末端操作器工作空间仿真如图6所示.

图6 机器人末端操作器工作空间仿真图

4.3 机器人末端操作器轨迹仿真

针对不同的零件,需要设计不同的末端操作器运动轨迹.在坡口切割过程中,为保证坡口切割质量,需要保证机器人各关节电机的运动的平稳性与准确性.因此末端操作器轨迹设计是否合理,就取决于末端操作器轨迹路径点集的选取.五轴坡口切割机器人的末端操作器轨迹规划[19-20]是以机器人视觉模块生成的零件轮廓点集为路径进行规划和执行的.轨迹规划的目的是对预定路径的设计,包括起终点之间的路径点的选择以及各段路径的规划,保证机器人可以在全段路径中均可以平稳运行,无加速度和速度的突变.

平板类零件的末端火焰枪轨迹路线为一条直线.因此对于机器人末端操作器直线类的轨迹规划问题,无论是在笛卡尔空间还是在关节空间,规划出的运动曲线是相同的一条直线,如图7所示.

虽然关节空间和笛卡尔空间内的轨迹规划原理相同,但是关节空间的规划需要对每个关节就行规划,计算每个关节的插补点.而笛卡尔规划是在笛卡尔空间规划末端轨迹,其只针对于末端操作器进行规划,然后再去逆解每个插补点,计算对应的每个关节的角度.由于规划的轨迹为直线类型,因此求逆解的计算量相较于对每个关节进行规划分析的计算量少,且末端操作器的五次插值运算简便,可以实现很好的仿真效果.因此本文只在笛卡尔空间内部进行规划和仿真分析，采用MATLAB软件配套的五次多项式轨迹插值jtraj函数对五轴坡口切割机器人轨迹进行笛卡尔空间内运动学仿真.

设定需要切割的零件为700 mm×400 mm尺寸的厚度均匀的平板零件(零件一端厚度50 mm,另一端厚度100 mm),坡口角度v=π/4.根据机器人机架和零件的相对位置,设定相对坐标确定零件加工的坡口加工位置,如图8所示.设定零件轨迹切割轨迹路径点集为

qA=[0,0,0]；qB=[100,100,50]；

qC=[800,100,50]；qD=[800,500,50]；

qE=[100,500,50].

故根据零件坡口切割要求,可以规划出不同的零件切割轨迹.零件的切割轨迹不同,其切割速率、切割精度和切割破坏性不同.我们可对不同的切割方案进行仿真实验比较,从而选出一个合理方案. 利用MATLAB进行编程,设定时间与步长,然后对可获取的轨迹进行仿真.

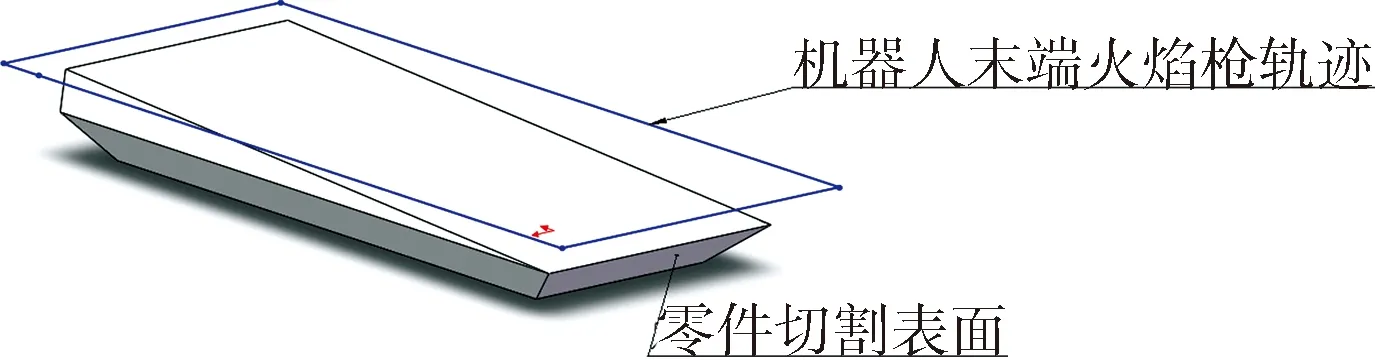
图7 机器人末端火焰枪轨迹示意图

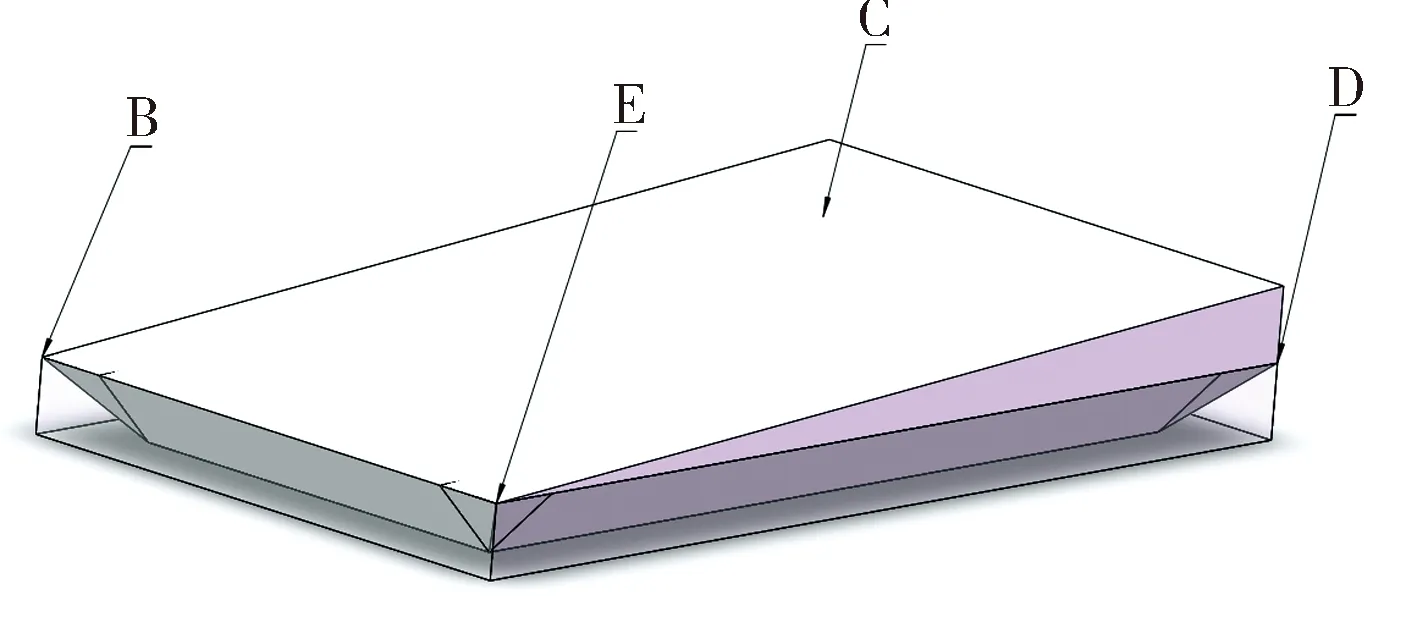
图8 零件切割示意图Fig.8 Schematic diagram of part cutting

方案1的零件规划路径为：

qA=[0,0,0，0,0]→

qB1=[100,100,50，pi/3,pi/4]→

qC1=[800,100,50，pi/3,pi/4]→

qC2=[800,100,50，5pi/6,pi/4]→

qD1=[800,500,50，5pi/6,pi/4]→

qD2=[800,500,50，4pi/3,pi/4]→

qE1=[100,500,50，4pi/3,pi/4]→

qE2=[100,500,50，11pi/6,pi/4]→

qB2=[100,100,50，11pi/6,pi/4]→

qA=[0,0,0,0,0].

方案2的零件规划路径为：

qA=[0,0,0，0,0]→qC1=

[800,100,50，pi/3,pi/4]→

qB1=[100,100,50，pi/3,pi/4]→

qB2=[100,100,50，11pi/6,pi/4]→

qE2=[100,500,50，11pi/6,pi/4]→

qE1=[100,500,50，4pi/3,pi/4]→

qD2=[800,500,50，4pi/3,pi/4]→

qD1=[800,500,50，5pi/6,pi/4]→

qC2=[800,100,50，5pi/6,pi/4]→

qA=[0,0,0,0,0].

方案1的机器人末端操作器轨迹仿真如图9所示,机器人各关节运动曲线如图10所示.方案2的机器人末端操作器轨迹仿真如图11所示，机器人各关节运动曲线如图12所示.

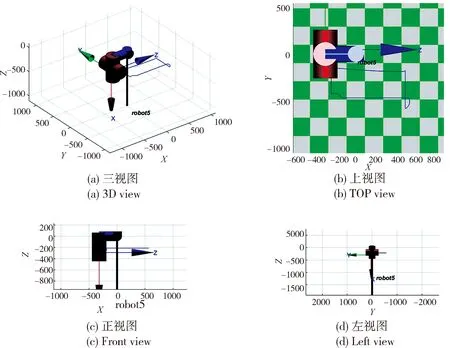
图9 机器人末端轨迹仿真(方案1)Fig.9 Simulation of robot end trajectory(scheme 1)

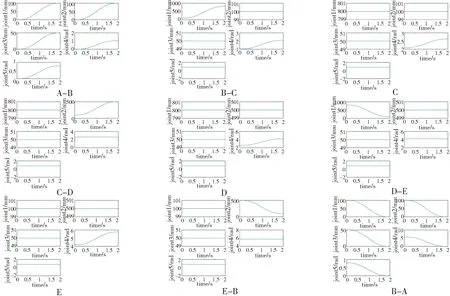
图10 机器人各点之间各关节运动曲线图(方案1)Fig.10 Motion curve of each joint between the robot points (scheme 1)

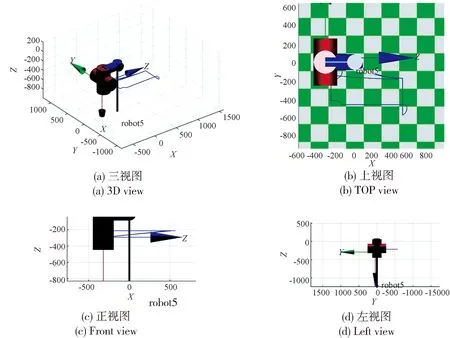
图11 机器人末端轨迹仿真(方案2)Fig.11 Simulation of robot end trajectory (scheme 2)

图12 机器人各点之间各关节运动曲线图(方案2)Fig.12 Motion curve of each joint between the robot points (scheme 2)

通过对方案1和方案2中机器人末端操作器的轨迹生成和机器人各关节的运动曲线的分析可知,两个方案的轨迹规划都可达到机器人末端操作器运动轨迹准确、各点处机器人各关节运动平稳和无速度突变的要求.通过方案2的运动仿真图和实际加工要求可知,方案2存在一些问题.首先方案2中坡口切割初始点为C点,C点与A点的距离较B点与A点之间的距离远,当火焰枪由零位运转到初始位置,方案2较方案1的路径较长,且由于C不是零件的端点,因此在实际加工的过程中,对于初始点的切割定位会较方案1误差大.其次由于在坡口切割过程中初始切割会对零件造成一定的破坏,方案1 中初始位置B点为零件端点,破坏性较小,而方案2初始点C为零件中部,相较于方案1,可能会对零件造成损坏.因此通过仿真实验推定,方案1设计的零件切割路径点集较为合理,验证了本文设计的机器人运动轨迹规划的合理性.

5 结 论

对于五轴坡口切割机器人的运动学仿真,本文根据坡口作业要求进行了坡口切割机器人的结构设计,根据机械结构建立了机器人的D-H参数坐标系,推导了其正逆运动学模型,通过MATLAB数值计算与仿真,验证了设计的机器人模型否可以满足坡口切割的加工要求；采用蒙特卡洛随机数算法生成机器人末端操作器工作空间,模拟出了机器人末端操作器的运动区域；采用五次多项式差值算法,实现了末端操作器的轨迹规划,验证了不同方案下机器人末端操作器轨迹路径点集选取的可行性,对机器人末端轨迹规划进行了一定的优化.通过实验仿真,为五轴坡口切割机器人的实际轨迹规划提供了理论支撑,为以后的动力学仿真与控制算法研究奠定了基础.