基于强度衰减的Vajont 滑坡运动特征非连续变形分析

张迎宾 ，董 琰 ，陈岩岩 ,2，李小琴 ，富海鹰 ，程谦恭 ，魏江涛

（1. 西南交通大学土木工程学院，四川 成都 610031；2. 中国市政工程西北设计研究院有限公司，甘肃 兰州730000；3. 西南交通大学地球科学与环境工程学院，四川 成都 610031）

1963 年10 月9 日，意大利Vajont 水库南岸的TOC 山体突然破坏，约2.5 亿立方米的岩体以大于20 m/s 的速度冲向水库，激起超过200 m 高的涌浪，漫过坝顶的蓄水沿着山谷一路淹没了包括隆加罗内镇在内的数个村镇，2 000 多人因此遇难[1-3]. Vajont滑坡因其复杂启滑机理、高速运动机制及严重致灾后果在学术界引起持续反响[4-5]. Hoek 将此滑坡事件定义为现代岩石力学和岩石工程学的起始点[6].

但目前对Vajont 滑坡的启滑机理以及高速运动现象仍存在较大争议. 争论点[6]主要集中于：滑坡渐进失稳启动机制；滑坡速度剧变、高速下滑运动的原因；滑坡“一体化”运动行为以及堆积体的层序性完整特征等. 其中，高速下滑是造成严重灾害的主因[5]. Müller[1]调查研究后认为Vajont 滑坡滑面强度存在衰减现象，使得滑体势能最大化转化为动能；Cecinato 等[7]研究了滑带强度衰减幅度，发现滑坡运动过程中，滑带内摩擦角由22° 降低到4°；Hendron等[3]基于运动过程计算分析，认为滑带强度衰减幅度可达50%. 对于强度衰减的原因，Habib[8]认为深层滑坡滑面高应力剪切的加热作用将孔隙水汽化，产生低摩阻滑动垫层；亦有学者[3,9-12]认为加热作用使得孔隙水压上升，降低了滑面上的有效应力或造成滑带发生应变软化，Hu 等[13]通过调查实验，发现这一机制同样存在于大光包滑坡中；但Tika 等[14-15]认为，剪切热量不足以汽化孔隙水形成低摩阻气垫，通过实验论证，快速剪切时黏土强度大幅降低，即强度衰减可能是岩土体固有的一种剪切特性. 迄今为止，Vajont 滑坡高速下滑机理虽颇富争议，但滑带强度衰减已成为重要观点. 但已有成果中滑带强度衰减对Vajont 滑坡运动能力、堆积特征的确切影响关注较少. 同时，值得探讨的是，上覆岩土体强度由于内部剪切行为的存在是否同样会发生衰减，继而与滑带强度衰减共同作用，造成Vajont 滑坡骤然启动、“一体化”高速下滑、保持原层序堆积.

由于高速滑坡成因机理复杂，控制因素众多，对其运动堆积行为，难以实现具有较大意义的试验研究[16]. 非连续变形分析（DDA）方法作为一种针对不连续岩土体运动模拟的计算方法，已广泛运用于研究岩土工程领域非连续性变形问题[17-23]. 本文结合滑坡历史资料，通过对意大利Vajont 滑坡进行现场调查，基于岩土体剪切强度衰减理论，利用DDA 方法，探讨滑带强度衰减、滑体强度衰减及其共同作用对Vajont 滑坡独特运动堆积特征的影响.

1 地质结构特征及物理模型

1.1 地质背景

意大利Vajont 滑坡位于阿尔卑斯山脉南部的Vajont 峡谷南侧（见图1），由于区域造山活动，地质构造复杂[24]. 峡谷两岸山体长期受到河流侵蚀、挤压抬升等构造作用，使里阿斯统—始新世岩层逐渐变形，在N-S 向（北-南向）形成典型的向斜结构.

图1 Vajont 滑坡的位置Fig. 1 Location of the Vajont landslide

野外调查发现，峡谷两岸岩层主要由中-上侏罗统到上白垩纪石英质灰岩和泥灰质石灰岩构成，其层序清晰有致，产状近乎水平（见图2），包含4 个不同形成时期、不同厚度的岩层（见图3[6]）. 钻孔记录表明，山体在深部“Fonzaso”构造地层产生破裂面，继而发生失稳致滑[6].

图2 Vajont 峡谷两岸地层状况Fig. 2 Stratigraphic conditions on both sides of the Vajont Valley

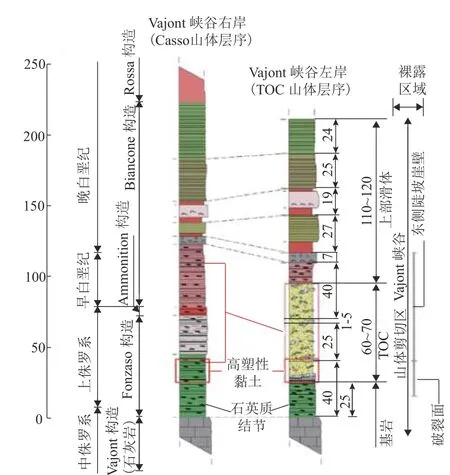
图3 更新的Vajont 峡谷两岸的地层序列（单位：m）Fig. 3 Updated lithostratigraphic columns on both sides of the Vajont Valley (unit: m)

1.2 滑源区特征

滑坡位于Vajont 峡谷南岸，半壁山体呈“一体化”下滑，滑动面整体较光滑连续，东侧略有阶状起伏，滑动面整体呈“椅状”，上部高陡，下部平缓，坡度在0°～40° 之间，是典型的坡脚型滑坡. 后缘岩壁断裂处形状为“M”状，东西向展布（见图4）.

图4 Vajont 滑坡俯视图Fig. 4 Vertical view of the Vajont landslide

1.3 滑带特征

Semenza 等[25-26]在早期调查中就指出，滑带区域的岩石地层之间夹存着厚度不等（0.1～10.0 cm）的黏土层. 在对该区域进行深入调查之后发现，滑带岩层之间确认存在高塑性黏土层[6,14-15]，剪切试验[3]表明，其残余强度可能在5°～16° 之间，黏土层的存在可能显著地影响着斜坡在各阶段的反应. Paronuzzi等[6]总结了Semenza 的调查结果，并通过对东、西两侧裸露在外的边界和残留在滑裂面上的剪切区域材料的详细分析，发现剪切区是由褶曲严重的岩石块体、角砾和高塑性的黏土夹层等混杂构成.

1.4 滑坡堆积区

现场调查发现，滑坡堆积体中除部分砾石状碎屑外，存在大量整体性较高的岩层，这些岩层呈现出与滑源区极度相似的地层层序（见图5（a）. 运动较远距离、停积在北岸山体上的滑坡飞来峰同样具有较大整体性（见图5（b））. 这表明Vajont 滑坡运动时可能具有“一体化”特征.

图5 滑坡堆积体及“飞来峰”的层序保持良好Fig. 5 Well-preserved strata sequence of klippe and slide deposit

2 模型建立

2.1 计算模型及参数取值

DDA 可充分考虑岩土体的非连续性，兼顾块体单元的小变形与大位移，在满足“不嵌入、无张拉”条件下，由Hamilton 原理与势能最小原理联立求解，对非连续性岩质滑坡的运动研究具有重要意义[27].

据研究[28]得知，滑坡西侧在整个破坏过程中起主导作用，且此处剖面为“椅状”，能反应Vajont滑坡典型剖面特征，具有代表性，所以选Hendron[3]等描述过的剖面（见图6）作为计算截面，并根据南北走向和东西走向的主要节理产状，建立Vajont滑坡DDA 计算模型（见图7）.

图6 滑坡横截面示意Fig. 6 Schematic diagram of landslide section

图7 DDA 计算模型（模型A）Fig. 7 Calculation model of DDA (model A)

关于参数取值的研究有很多，Boon 等[29]对前人学者所采用的参数做了相关整理，并对Vajont 滑坡的稳定性进行了分析；Superchi[30]通过剪切实验分析了Vajont 滑坡滑体岩石材料的性质. 但是，在利用数值方法对滑坡进行模拟研究时，尚未有统一的参数取值. 为了使参数尽量符合实际情况，本文在众多学者的研究成果基础上，利用经验法计算滑坡的相关物理参数，并讨论参数对滑坡稳定性的影响，最终采用的计算参数如表1～3.

表1 Vajont 滑坡的物理参数Tab. 1 Physical parameters of the Vajont landslide

表2 节理参数Tab. 2 Joint parameters

表3 模型控制参数Tab. 3 Model control parameters

2.2 强度衰减

滑坡抗滑能力一定程度上可由岩土体抗剪强度表征，根据摩尔-库伦准则，滑体及滑带抗剪强度为

式中：σ为剪切破坏面的法向应力；φ内摩擦角(φs为滑带内摩擦角，φj为滑体内摩擦角).

Nonveiller[9]认为滑坡失稳前，滑面及滑体的强度并非是峰值强度，因而本文取坡体衰减前稳定阶段的强度为临界状态强度，用τc表示，滑坡失稳溃滑阶段的强度则由τs表示. 强度衰减程度由强度衰减率k表示，如式（2）.

滑坡临界状态强度采用强度折减法[31-32]获取，由于复杂因素致滑的岩质斜坡常常呈现脆性失稳，缺少鲜明的征兆作为失稳指标，因而需要兼顾边坡变形与块体位移综合判断[33]，本文采用Maclaughlin等[33-34]以位移计算收敛作为判据的方法求解τc：① 坡体前缘位移是否收敛在某一范围内（小于斜坡南北向宽度的1‰，即 < 1.2 m）；② 坡体后缘与基岩之间是否有明显张裂缝出现.

监测块体1，计算结果如图8 所示，可知：滑带内摩擦角折减至21.0° 时，位移不再收敛，滑坡整体逐渐脱离基岩，后缘张开，前缘持续蠕滑（见图9）.

图8 不同内摩擦角时最前缘块体 1 的位移时间曲线Fig. 8 Displacement-time history of the leading edge block 1 with different friction angles

图9 φs = 21.0°，Vajont 斜坡模型最终的状态Fig. 9 Ultimate state of the Vajont slope model with φs = 21.0°

故取滑坡临界状态的滑面内摩擦角为23.0°，这与Cecinato 等[7]的结论相吻合. 以此为基准，当滑坡失稳溃滑后，滑带强度剧烈衰减，取衰减率(内摩擦角)k为30%（6.9°）[14]、40%（9.2°）、50%（11.4°）[3]、70%（15.8°）. 众多学者[3,6, 35]通过对滑坡区地质的调查发现，滑带是由较为松散及碎屑化的岩石地层构成，且夹杂着厚度不等的黏土层，因而在计算时一般假定滑带的黏聚力为0.

3 滑坡高速运动分析

3.1 运动特征分析

上一节分析得到，滑带的临界内摩擦角为23.0°，以此临界角为基准，计算滑坡在完全启动后，滑带强度急剧衰减为稳定阶段临界强度的30%、40%、50%、70%，对应的内摩擦角分别为6.9°、9.2°、11.4°、15.8°的最终运动堆积状态. 需要指出的是，在此过程中滑体强度不变，设定φj= 30.0°，滑体c= 2.5 MPa.

在不同滑带摩擦角状态下，DDA 模拟滑坡的最终运动堆积状态如图10 所示（Vajont 滑坡实际堆积轮廓线以红色虚线表示在图中）. 从最终模拟结果分析得到，当滑带内摩擦角降为6.9° 时，也即滑坡完全启动后滑带强度降低至稳定阶段强度的30%时，DDA 计算模拟滑坡的最终堆积轮廓线与滑坡实际堆积轮廓线较为吻合.

图10 φs 衰减至不同值时DDA 模拟滑坡的运动全过程（φj = 30.0°）Fig. 10 Whole process of landslide motion by DDA simulation with the sliding band strength φs decaying to different values（φj = 30.0°）

图11 为最后缘块体2 的位移时程曲线及中部块体3 的速度时程曲线. 由图可知：滑带强度降低越明显，则摩阻力越低，滑坡的运动能力则越强. 表4为监测所得的中部块体3 的最大速度.

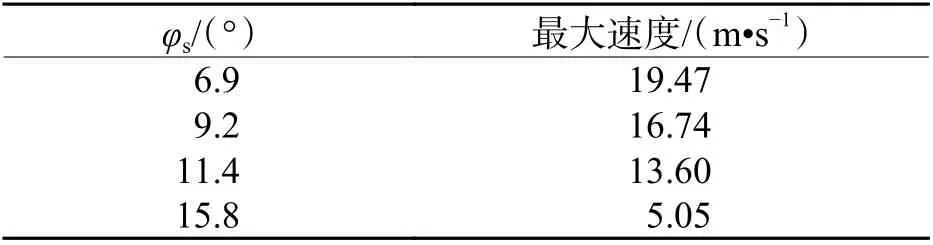
表4 滑带内摩擦角不同时滑坡的最大速度Tab. 4 Maximum velocities of the landslide with different friction angles of sliding band

图11 φs（滑带强度）衰减至不同值时监测块体的位移及速度时程曲线（φj = 30.0°）Fig. 11 Time histories of velocity and displacement for monitored blocks with the sliding band strength φs decaying to different values (φj = 30.0°)

通过观察DDA 模拟Vajont 滑坡的运动过程（图10）可发现：此运动过程具有典型的“一体化”特征，并且这种持续高速化运动是发生在前30 s内，这主要是由于滑坡是在瞬间启动的，因此其动能是在极短时间内由势能转化而来，从而使滑坡有了很大的初速度，并加速下滑，后缘块体的势能相对较小，这是由于在下滑过程中受到摩阻力的影响，其大部分势能同样转化为动能，并推动前缘块体一起整体向前滑动. 由于对岸有山体，滑坡体到达对岸后受到阻拦，向前运动趋势受阻，且后缘块体的势能也在不断降低，从而不能提供足够大的动能推动前缘块体继续向前运动，最终导致整体运动速度开始减小，并停积下来. 图10 可直观看出，滑带强度衰减越显著，滑带的摩阻力越低，势能能够大量的转化为滑坡的动能，而滑带强度衰减值较小时，坡体“向前”的能力明显较小.

堆积体的层序性保持完整是滑坡的特征之一.本文作者通过对Vajont 滑坡进行实地考察，发现“飞来峰”的地层保持良好，其原因是滑坡运动的“一体化”，从图10 也可发现得知. 通过DDA 数值模拟发现，前缘滑体的运动更像是后缘滑体在逐步推着向前运动.

3.2 滑体强度变化对滑坡运动的影响

在DDA 等离散方法中，节理强度用来表征滑体的强度. 由3.2 节可知，可取稳定阶段滑体节理内摩擦角φj= 40.0° 为临界状态值，研究发现[21]黏聚力的取值对滑坡运动影响不大，因此在此部分计算中忽略黏聚力，即不考虑节理面粘结对滑坡过程的影响. 在DDA 计算模型中，滑带的内摩擦角保持不变（φs=9.2°），假定节理强度分别降低为临界状态的100%、70%、40%、30%，对应的节理内摩擦角为40.0°、30.0°、19.0°、14.0°，不同条件下模拟的滑坡最终堆积形态如图12 所示. 同时记录模型后缘块体2 的位移时程曲线、中部块体3 的速度时程曲线（图13）.

图12 不同φj 时滑坡最终堆积形态（φs = 9.2°）Fig. 12 Ultimate deposit outline of models with the sliding mass strength φj decaying to different values (φs = 9.2°)

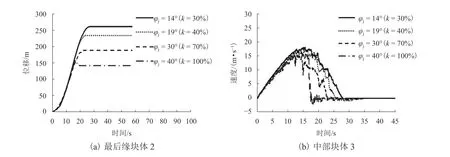
图13 φj（滑体强度）衰减至不同值时，监测块体的位移时程曲线（φs = 9.2°）Fig. 13 Displacement-time history of monitored blocks with the strength of slide mass φj decaying to different values (φs = 9.2°)

对比图11、13 可知：相较于滑带强度衰减对滑坡运动能力的影响，滑坡强度的衰减对滑坡运动能力的影响不显著. 从图12 来看：当节理内摩擦角为14.0° 时，模型最终堆积形态与实际堆积情况（红线轮廓虚线）最为吻合. 当滑体节理强度未衰减，即在滑坡过程中内摩擦角一直是40.0° 时，滑坡向前运动的距离相对较近（图12（d）），其主要原因为滑体强度较高，降低了滑坡中上部向前推动的能力，从而使整体向前运动的能力相对较弱. 从4 个模型最终堆积形态（图12）来看，随着滑体强度的衰减，向上“爬至”对岸山体的滑坡前缘堆积块体数量越多.从上述分析来看，滑体强度的变化影响滑坡整体向前向上的运动能力.

3.3 讨 论

通过对滑坡稳定阶段及失稳高速运动阶段强度变化计算对比，得出斜坡突然失稳并高速滑动的原因是滑带、滑体强度的急剧衰减，且强度衰减越快，滑体下滑速度越高. 从上述计算结果来看，滑带强度的衰减变化对滑坡运动能力的影响相对较大，而滑体强度对中上部岩石滑体的爬坡能力影响较大. 在实际高速滑坡过程中，滑体和滑带材料的剪切强度衰减是同时同步的，滑带强度的衰减和滑体强度的衰减一起造成了滑坡的高速运动，二者缺一不可. 通过分析滑带区域夹层黏土的剪切实验可以看出[14]，剪切法向应力较大时，随着剪切位移逐渐增大，黏土的强度迅速降低，当剪切速率逐渐增大且在浸水条件下，这种强度弱化更加显著，逐渐表现出流态[15].类似强度弱化的性质在岩石及岩石节理在剪切时同样存在[36]. 在Vajont 斜坡完全溃滑前，因水位的不断升降，斜坡遭受扰动且在很长一段时间内处于蠕滑阶段，在此期间，斜坡内部完整岩石的应变、应力由于剪切作用不断发生变化，导致完整岩块不断破裂，这些都造成了滑体强度的进一步降低.

4 结 论

本文在Vajont 滑坡的地质状况和相关现象的基础上，通过利用DDA 方法对Vajont 滑坡的运动过程进行模拟，重点对Vajont 滑坡在滑坡破坏前后强度衰减影响下的运动能力变化进行了分析，对滑坡的一些运动特征进行了揭示.

1） 相比于滑坡稳定阶段，滑带及滑体的强度在Vajont 滑坡完全启动后有了明显降低，这造成了Vajont 滑坡突然的溃滑及高速运动. 滑带强度及滑体强度的共同衰减变化造成了滑坡的加速下滑.

2） 目前大多数研究主要集中于探讨滑带强度变化对滑坡运动能力的影响，本文不仅探讨了滑带强度变化对滑坡运动能力的影响，还分析了滑体强度不同程度的衰减对滑坡运动能力的影响，结果表明，在同样程度的衰减情况下，滑带强度变化对滑坡运动能力的影响更大，而滑体强度的变化是在此基础上促进了滑坡前缘块体的爬坡能力，这在一定程度上影响对岸工程设施的安全性能.

3） 对Vajont 滑坡进行了实地考察，察看了飞来峰的地质保存情况，发现滑体残迹保持了较好的产状和层序性. 从DDA 模拟Vajont 滑坡的运动过程来看，滑坡运动体现了“一体化”运动的特征，这也是层序保持良好的原因之一. 从模拟过程来看，“椅背”滑体的势能转化为动能，若滑坡摩阻力较小，势能大部分转化为动能，促使滑体整体向前运动.

4） 通过对DDA 模拟结果分析得出，滑坡完全启动后，滑带强度至少衰减至稳定阶段的30%～40%，滑体强度衰减至稳定阶段的30%～70%.