高速列车抗蛇行减振器参数的多目标优化研究

姚 远 ，陈相旺 ，李 广 ，张振先 ,2

（1. 西南交通大学牵引动力国家重点实验室，四川 成都 610031；2. 中车青岛四方机车车辆股份有限公司，山东 青岛 266111）

在高速列车车体和转向架间沿纵向布置抗蛇行减振器可以增加车体与转向架之间的回转力矩，有效地抑制车辆的蛇行运动，保证车辆系统具有足够的横向运行稳定性，确保了行车安全和旅客乘坐舒适性. 作为高速列车的重要悬挂元件，抗蛇行减振器悬挂参数的优化设计显得尤为重要. 针对抗蛇行减振器对车辆动力学性能的影响已经开展了诸多研究[1-4]，试图找到减振器参数对车辆动力学性能的影响特点，从而为参数的优化设计提供参考. 采用主动抗蛇行减振器虽然可以有效地兼顾车辆横向稳定性与曲线通过性能[5]，但其成本较高、部件繁多、维修保养不便，针对传统的被动悬挂参数进行优化仍是提升车辆动力学性能的有效方法.

机械系统的设计优化旨在从复杂和矛盾的设计标准中寻求有效折衷的设计准则，从而兼顾各项指标，实现良好的性能要求[6-7]. 铁道车辆的悬挂参数设计是典型的多目标优化问题，需要找到合理的悬挂参数，使其兼顾车辆的横向稳定性、曲线通过性能和乘坐舒适性等性能指标. 解欢等[8]以提升车辆运行平稳性和稳定性为目标，选择混合代理模型，通过多目标优化方法获得了优化悬挂参数. Johnsson 等[9]针对车辆的运行安全性、舒适性和车轮磨耗问题，对阻尼元件进行多目标优化设计，并加入了自适应控制策略进一步提升车辆性能. Bideleh 等[10]建立了50 个自由度的铁道车辆仿真模型，并考虑一、二系悬挂布置方式的对称性，通过参数灵敏度分析选取主要悬挂参数，借助遗传算法解决车辆轮轨磨耗和舒适性的优化问题. 目前，铁道车辆悬挂参数的优化集中于寻求兼顾车辆稳定性、曲线通过性能、运行平稳性、车轮磨耗性能的折衷设计.

高速列车横向稳定性是转向架悬挂参数设计中最为关注的性能，在悬挂参数优化中要考虑车辆在不同结构参数和轮轨接触状态下的稳定性，列车在低等效轮轨接触锥度和高等效锥度时分别容易发生一次蛇行和二次蛇行运动失稳，抗蛇行减振器参数的优化设计需要兼顾列车两种轮轨接触状态下的运行稳定性. 本文基于高速列车在高、低两种轮轨接触锥度状态下的线性稳定性，对抗蛇行减振器参数进行多目标优化，同时分析影响抗蛇行减振器参数优化结果的因素，挖掘车辆悬挂参数之间的匹配规律，为抗蛇行减振器的选取提供有效理论支撑.

1 车辆动力学模型与健壮稳定性

1.1 车辆线性动力学模型

针对国内运行的典型高速列车结构参数，建立简化的车辆横向动力学模型，如图1 所示，图中：v为速度；Kpx、Kpy分别为一系纵向和横向刚度；Ksx、Ksy分别为二系纵向和横向刚度；Csx、Kncsx分别为抗蛇行减振器阻尼及其串联关节刚度；Csy、Kncsy分别为二系横向阻尼及其串联关节刚度. 模型由7 个刚体组成，包括1 个车体、2 个构架、4 个轮对，其中：车体具有横移、摇头、侧滚3 个自由度；轮对和构架分别具有横移、摇头2 个自由度. 一系悬挂位于轮对与构架之间，由横向和纵向定位刚度组成；车体与构架之间设有二系横向、纵向、垂向刚度及阻尼，并考虑了抗侧滚刚度，考虑到液压减振器橡胶节点刚度和液体刚度的影响，二系横向和纵向减振器采用刚度和阻尼串联的Maxwell 模型可以满足分析精度要求[11]，该模型共27 个自由度. 本文主要针对车辆线性稳定性进行分析，用等效锥度来表示轮轨接触几何特征，采用Kalker 线性理论计算轮轨切向力.

图1 车辆横向动力学简化模型Fig. 1 Simplified model of vehicle lateral dynamics

车辆系统动力学方程为

式中：x为系统的自由度矩阵；M、C、K和Q分别为系统的质量矩阵、阻尼矩阵、刚度矩阵和外力矩阵.

对于弹性定位单个轮对的运动方程，轮轨切向力作用使得轮对的横移和摇头耦合[12-13].K是非对称矩阵，其非对角线项表示轮轨切向接触引起的轮对横移和摇头运动的耦合作用. 阻尼矩阵C与运行速度v有关. 在蛇行运动的一个周期内，如果输入能量和消耗能量是相等的，此时线性系统处于临界稳定状态，对应的速度称为线性临界速度.

由于刚度矩阵K的非对称特性，通过传统的模态分析方法不能将式（1）转换为解耦的微分方程组，而采用复模态变换则可以实现. 将式（1）改写成状态空间形式，如式（2）.

式中：y为系统状态变量矩阵；A为系统矩阵，如式（3）.

式中：I为单位矩阵，通过分析A的特征值和特征向量可以得到车辆系统的线性稳定性指标和模态振型.

1.2 健壮稳定性

抗蛇行减振器对车辆系统动力学性能有重要影响，主要反映在车辆的横向平稳性、曲线通过性能以及蛇行运动稳定性. 而对于高速运行的动车，车辆蛇行稳定性是最重要的指标，在转向架悬挂参数的优化中应重点关注.

转向架悬挂元件在设计、制造和维修的过程中会不可避免的出现误差，液压减振器及其橡胶关节在服役中随着时间推移发生故障或蠕变，悬挂阻尼或刚度发生变化会直接影响车辆动力学性能；另外，轮轨磨耗和线路变形导致轮轨接触几何关系改变，同样会影响车辆的动力学性能. 当轮轨接触锥度较低时，如新轮、新轨状态以及轨底坡增大，由于较低的蛇行频率与车体振动频率耦合，车辆容易发生一次蛇行，车体出现低频横向晃动，影响车辆乘坐舒适性甚至安全性；车轮踏面磨耗后出现较高的轮轨接触锥度使得车辆稳定性裕度不足，发生二次蛇行，导致转向架出现高频横向剧烈振动. 因此，车辆需要在较宽的速度范围和轮轨接触状态具有足够的稳定性裕度，以防止悬挂参数改变和等效锥度变化引起的稳定性削弱，即车辆具有健壮稳定性. 对于上述车辆横向线性动力学模型，通过计算系统矩阵的特征值，将蛇行运动模态对应特征值的实部与特征值模数的比值，即系统阻尼比定义为系统线性稳定性指标ζ.本文选取较小值作为优化方向，通常阻尼值为正表明系统是稳定的，故定义ζ为负值对应系统是稳定状态.

本文将速度200 km/h、轮轨接触低锥度（λ=0.05）工况和速度350 km/h、轮轨接触高锥度（λ=0.40）工况下的稳定性作为优化目标，分别定义为低锥度稳定性指标ζlow和高锥度稳定性指标ζhigh，值越小对应车辆在该工况下的蛇行运动阻尼越大，其稳定性就越好.

2 抗蛇行减振器参数多目标优化

2.1 多目标优化设计

对于单目标优化问题，往往可以找到全局最优解，使得优化目标最为理想. 而对于多目标优化问题，由于优化目标间可能存在冲突并且无法比较，所以往往很难找到一个解使得所有目标函数同时最优. 一个解对于其中一个目标函数来说是最优的，而对于其他目标函数可能不是最优，甚至是最差的，这样的解就所有目标函数而言没有优劣之分. 因此，在多目标优化问题中，通常存在着一个解集，这个解集称为Pareto 集，其包含的解称作Pareto 最优解，Pareto最优解在目标函数空间中的像称为Pareto 前沿. 根据设计侧重点的不同，可以人为地在Pareto 集中选取满足性能要求的优化解.

本文选取Csx及Kncsx作为优化参数，取值范围分别为300～4 000 kN•s•m−1、5～40 kN•mm−1. 优化目标为车辆系统的低锥度稳定性指标和高锥度稳定性指标，此多目标优化问题可以描述为min{ζlow，ζhigh}.

NSGA- Ⅱ算法是在非支配排序遗传算法 （NSGA）基础上改进而来，不再需要参数共享，能够保持种群的多样性，提高计算效率，是目前解决多目标优化问题常用的一种有效算法[14-15]. 因此本文选用带有精英策略的快速非支配排序遗传算法（NSGA-Ⅱ）进行多目标优化设计，算法中大多数默认设置保持不变，设置群体数量为3000，代数目为20.

2.2 多目标优化结果

采用遗传算法NSGA- Ⅱ对抗蛇行减振器的两个设计参数进行多目标优化，通过不断迭代和更新悬挂参数以获取针对优化目标更佳的车辆动力学性能，得到关于此多目标优化问题的Pareto 前沿和Pareto 集. 本文首先针对目前国内两种典型的高速列车进行抗蛇行减振器参数优化设计，分别记作Type 1 和Type 2，其他的悬挂参数保持不变，详见表1. 图2 为得到的Pareto 优化目标前沿.

表1 两类高速列车悬挂参数Tab. 1 Suspension parameters of two types of high-speed trains

图2 两种悬挂参数对应的最优线性稳定性指标Fig. 2 Optimal linear stability indexes corresponding to two types of suspension parameters

Pareto 前沿反映了优化目标ζlow和ζhigh之间的矛盾关系，即车辆的低锥度稳定性越好，其高锥度稳定性就会越差. 这种关系突出了多目标优化设计的重要性，由于低锥度稳定性和高锥度稳定性不能同时取得最优，根据不同的设计选择，或侧重某一稳定性指标，或兼顾二者，设计人员可以从Pareto 集中选取满足车辆性能要求的Pareto 前沿，进而获取对应的抗蛇行减振器优化参数. 据图2 可知：Type 1 型列车悬挂参数可实现的最小ζlow和ζhigh分别为−0.40和−0.30，相比于Type 2 对应的−0.13 和−0.20，Type 1可实现的低锥度稳定性裕度和高锥度稳定性裕度均明显大于Type 2. 这是由于本文仅对抗蛇行减振器参数进行优化设计，两类动车其他悬挂参数原始取值存在着较大差异，如一系水平定位刚度、二系横向减振器阻尼等，这些悬挂参数对车辆的稳定性也有重要影响. 在给定的抗蛇行减振器参数优化范围内，可以使Type 1 型悬挂参数的低锥度稳定性和高锥度稳定性均较为理想；对于Type 2 型悬挂参数不论如何选取优化参数，两个稳定性指标很难同时得到保证，易出现蛇行运动稳定性不足的情况. 在实际服役过程中，允许Type 2 出现小极限环的蛇行失稳运动，其对车辆的运行安全和旅客乘坐舒适性不会造成太大影响，并且转向架装有轴箱报警装置，可以对车辆运行安全状态进行实时监测；Type 1 一旦出现蛇行失稳，其失稳状态是大幅值的极限环振动，要坚决避免[16]. 另外，本文选取的优化目标工况对于Type 2 来说比较极端，在车辆实际运营中通常不会出现. Type 2 型列车新轮的等效锥度为0.17 左右，随着车辆运行里程的增加其值一般会不断增大，当运行里程达到一定数值后会进行镟轮处理，避免了轮轨间的过高锥度接触，从而不会出现车辆高速运行时的轮轨接触高锥度失稳问题.

图3 是对两类列车悬挂参数进行多目标优化后得到的Pareto 集，反映了最优解的分布和优化目标之间的关系. 由图3 可知：对于Type 1，Csx的最优解分布较为集中，是给定优化参数的上限，因此，为保证车辆良好的稳定性，需要较大的抗蛇行减振器阻尼Csx；对于Type 2，Csx最优解取值较小，分布在600～1000 kN•s•m−1；两类列车目前采用的Csx数值与所得到的最优解分布相吻合，反映了本文所采用的多目标优化设计方法的合理与可靠性；Type 1 和Type 2 对应的Kncsx与不同轮轨接触锥度对应的车辆稳定性影响规律完全一致，即最优的Kncsx随ζlow的减小而减小，为保证良好的低锥度稳定性，Kncsx的取值应较小，相应地增大Kncsx有利于高锥度下的车辆横向稳定性.

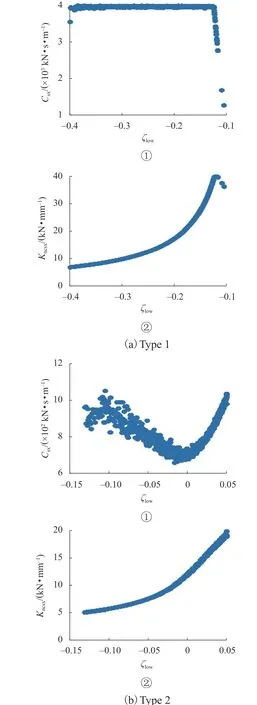
图3 最优的抗蛇行减振器参数Fig. 3 Optimum parameters of yaw damper

2.3 最优悬挂参数影响因素分析

根据车辆动力学理论，一系水平定位刚度Kpx、Kpy和二系横向阻尼Csy对车辆蛇行运动稳定性具有显著影响，且与抗蛇行减振器参数可能存在交互作用，分析其取值不同对抗蛇行减振器优化参数分布的影响.

首先分析Kpx对Csx和Kncsx最优解分布的影响，设置Kpx的取值范围为10～120 kN•mm−1，通过多目标优化得到不同Kpx对应的悬挂参数优化结果.图4 分别是Csy为40 kN•s•m−1和15 kN•s•m−1时的Pareto 集，从图中可以看出：Kpx取值对Csx最优解分布无明显影响；在Csy为40 kN•s•m−1时，不论Kpx取值的大小，对应Csx最优解均较大，接近优化上限4 000 kN•s•m−1；当Csy为15 kN•s•m−1时，对应不同大小的Kpx，Csx最优解均为较小值；Kpx的取值对Kncsx最优解的分布有一定影响，当Kpx取值较小时，对应的Kncsx匹配值要增加；Kncsx对车辆稳定性的影响与上文一致，增大Kncsx，车辆低锥度稳定性随之降低，高锥度稳定性随之提升.

图4 Csx 和Kncsx 最优解Fig. 4 Optimal values of Csx and Kncsx

选取Kpy的变化范围为3～15 kN•mm−1，分析其取值对抗蛇行减振器参数优化结果的影响，得到Csy=40 kN•s•m−1和15 kN•s•m−1时的Pareto 集，与一系纵向刚度Kpx的结果类似，Kpy的取值对抗蛇行减振器的参数优化结果影响不大；而Csy对抗蛇行减振器参数的最优解影响显著，较大的二系横向减振器阻尼可实现较好的低锥度稳定性. 为了进一步分析Csy对抗蛇行减振器最优解的影响，图5 为不同Csy数值下得到的Pareto 集，Csy的取值范围为10～50 kN•s•m−1. 图5（a）、（c）呈阶梯状分布，随着Csy取值的增大，对应的Csx最优解会由较小值突变到较大值，即：Csx最优解取决于Csy的值，Csy数值较小时，Csx最优解取值较小，大多不超过1 000 kN•s•m−1；Csy数值较大时，Csx最优解集中分布在数值较大区域，接近4 000 kN•s•m−1. 因此，为保证车辆良好的蛇行运动稳定性，在进行悬挂参数优化匹配设计时，要注意抗蛇行减振器阻尼和二系横向阻尼之间的匹配，即二者数值同时取较小值或者同时取较大值.Csy的取值对Kncsx优化解影响不大，在Csy较小时，可实现的低锥度稳定性裕度小于Csy取值较大时.

图5 不同Csy 对应的Csx 和Kncsx 最优解Fig. 5 Optimal values of Csx and Kncsx corresponding to different Csy

2.4 车辆稳定性根轨迹分析

进一步分析抗蛇行减振器橡胶关节刚度对车辆蛇行运动稳定性的影响，车辆运行速度为350 km/h时，车辆线性系统根轨迹随着Kncsx变化曲线如图6所示，图中：ζ ¯为模态阻尼比 ζ ¯ （系统矩阵特征值的实部与特征值的模数之比，ζ ¯为负值表示稳定状态，ζ¯> 0 时，车辆的蛇行运动失稳）；f为模态的衰减振动频率，是特征值的虚部. 每个根轨迹由26 个特征根组成，Kncsx变化范围为5～30 kN•mm−1，每个“+”表示相应的模态，较大的“+”对应较大的Kncsx. 大多数情况下，低频蛇行模态（1～5 Hz）决定了车辆的蛇行运动临界速度.

图6 随Kncsx 变化的车辆系统根轨迹曲线Fig. 6 Root loci of the vehicle system with the change of Kncsx

在低等效锥度时，频率低于2 Hz 的转向架蛇行模态的稳定性随着Knscx的增大而减小；在高等效锥度时，转向架蛇行模态的振动频率接近10 Hz，随着Kncsx的增大，蛇行模态的稳定性不断增强. 总之，增大Kncsx可以提升车辆在较高轮轨接触锥度状态时的稳定性，相反，减小Kncsx可以增强车辆在较低轮轨接触锥度状态时的稳定性，因此，Kncsx的选取需要平衡两种状态对应的稳定性. 另外，抗蛇行减振器关节刚度Kncsx对转向架蛇行模态频率几乎无影响.

3 结 论

1） 针对高速列车蛇行运动稳定性，定义了高、低锥度轮轨接触状态的稳定性指标，并以此为优化目标，采用基于NSGA- Ⅱ遗传算法的多目标优化方法对抗蛇行减振器参数进行优化分析，以增强不同轮轨接触状态下的车辆稳定性，提高车辆线路适应能力；

2） 优化的抗蛇行减振器阻尼值主要取决于车辆二系横向阻尼，较大的二系横向阻尼匹配较大的抗蛇行减振器阻尼，反之亦然；得出了两种阻尼值的抗蛇行减振器选配类型，即转向架单侧采用较小阻尼值约600～1000 kN•s•m−1，或者单侧阻尼值采用大于4000 kN•s•m−1的抗蛇行减振器；而抗蛇行减振器刚度显著影响不同轮轨接触状态下的车辆稳定性，较小的抗蛇行减振器刚度有利于低锥度车辆稳定性，增大刚度有利于车轮踏面磨耗后高锥度下的车辆稳定性.

致谢：感谢牵引动力国家重点实验室自主研究课题（2019TPL-Q07，2019TPL-Q08）支持.