山西省GNSS基准站时间序列噪声特征分析
2021-12-28穆慧敏宋志英杨林森
成 诚,穆慧敏,平 旗,宋志英,李 云,杨林森
(1.山西省地震局临汾地震监测中心站,山西 临汾 041000;2.山西省地震局,山西 太原 030021;3.太原大陆裂谷动力学国家野外科学观测研究站,山西 太原 030025;4.山西省怀仁市地震局,山西 怀仁 038300)
0 引言
“中国大陆构造环境监测网络”(以下简称陆态网络)项目是由中国地震局牵头,多部委共同建设的国家重大科技基础设施项目。2012年3月通过国家验收至今,陆态网络运行稳定,其建设经验已推广到海外[1-2]。陆态网络为在中国大陆及其周边地区开展大范围定量化地壳形变监测提供第一手数据,也为我国大地测量基准体系的建立、维持和自主卫星导航定位系统的建立奠定基础。此外,其还在探究地震孕育机理及地震预报研究中发挥出作用[3]。
山西地区共建设9个陆态网络连续基准站,积累多年观测数据,使用专业处理软件计算得到山西基准站高精度时间序列。时间序列中存在的噪声,分为与时间无关的白色噪声和与时间相关的有色噪声。白色噪声是一种随机信号,在功率谱上呈水平的功率谱密度。白色噪声之外的噪声统称有色噪声。Nilolaidis认为时间序列的噪声更接近于白色噪声和闪烁噪声的叠加。因忽略了这一点,速率估计的结果会存在一定偏差,尤其在地质条件和板块运动较为稳定的地区。由于位移量小,若低估观测噪声的误差影响,会导致地壳形变大小甚至方向上出现错误[4]。该文使用Simon D.P.Williams研发时间序列分析软件CATS,对山西省GNSS基准站时间序列进行频谱计算和最大似然估计值计算,并分析其噪声特征。
1 山西GNSS网时间序列与噪声分析方法
1.1 时间序列函数模型
时间序列中包含构造和非构造形变信息,非构造形变周期性成分不会对提取大尺度的构造运动产生影响,会造成参考框架存在周期性的变化[5]。该文使用中国地震台网中心发布的山西省GNSS基准站时间序列数据结果。
文献[6]的研究结果表明,从山西部分GNSS基准站时间序列图发现,N、E、U三个方向变化趋势相同,N、E方向时间序列呈线性变化,N方向向南运动,E方向向东运动,U方向时间序列呈周期性变化。对于GNSS时间序列的分析,通常要考虑长周期、同震变形及震后变形,一般用下列周期性模型表示[7]:
(1)
式中:ti以年为单位;系数a、b分别表示地壳位置和线性变化率;系数c、d、e和f描述周年和半周年运动振幅;系数gj表示地震造成的同震偏移;Ht为阶跃函数;vi为残差值即下文所指的噪声信号。应用该参考模型可有效估计基准站时间序列的季节性变化,同时,也能反映连续基准站的位置和速度信息。
由于研究与地壳形变无关的噪声信息,故对基准站时间序列按式(1)扣除线性项、周期项及各种原因造成的偏移量。采用Williams研发的时间序列分析软件CATS拟合式(1)中各系数,扣除时间序列的已知项,得到残差序列,对噪声特性进行分析。
1.2 频谱分析法
原始时间序列扣除已知项的噪声时间序列,可用频谱定性分析噪声类型。频谱分析是一种在频率域上分析信号的方法,可视为一种幂次法则。噪声时间序列在频谱域上的功率谱可使用Power Law的形式表示[8]:
(2)
式中:f为时间频率;P0和f0是正则化常数;k为谱指数。k值越大,表示噪声序列的时间相关性越高。
将式(2)取对数进行曲线拟合,运用最小二乘法可得到P0及k值。k值通常为-3 最大似然估计法是一种非线性最小二乘法,目的在于找到与时间序列最相近的模型参数。通过调整协方差矩阵使得似然函数取得最大值,得到与该时间序列最相近的噪声模型,就可通过协方差矩阵估算出时间序列中的噪声振幅大小。与频谱分析相比,最大似然估计法可定量计算噪声大小[9]。其公式为: (3) 式中:detC为矩阵的行列式;C为假定噪声的协方差阵;N为时间序列的长度;v为线性拟合后的残差,由C采用加权最小二乘法求得。协方差矩阵C可表达若干随机噪声过程,如,白色噪声(WH)、闪烁噪声(FN)、随机游走噪声(RWN)等及其各类组合[10-11]。 CATS软件是由Simon D.P.Williams研发计算时间序列的程序,能得到时间序列中包含线性部分和非线性部分的处理结果。其中,线性部分使用最小二乘法计算截距、斜率、偏移及周期信号的振幅,非线性部分采用线性计算后的残差求特定噪声模型的参数和振幅大小[12]。 在自然界噪声中,不同的谱指数对应不同的噪声特性。应用CATS软件频谱分析模块计算山西各站扣除已知项时间序列分量的谱指数(见表1)。 表1 山西GNSS基准站功率谱计算结果 由于山西各基准站所处环境不同,产生噪声的来源可能会有差异,噪声特性可能也不相同。根据前人研究成果,选取WH、WH+FN、WH+RWN、WH+FN+RW 4种噪声模型,采用CATS软件计算9个参考站各类噪声模型组合的最大似然估计值(见第40页表2)。 谱指数结果可直接揭示山西GNSS基准站时间序列的噪声特性,同时,还可采用不同噪声模型下最大似然估计值的比较来研究噪声特性[13]。山西GNSS基准站坐标时间序列的谱指数结果如表1所示。表中站点为GNSS基准站站名,N、E、U分别为各基准站坐标时间序列的三个方向分量谱指数值。可以看出,山西9个GNSS基准站时间序列各分量的噪声谱指数都为负值(-2~0),表明各分量不仅有白色噪声,也包含有色噪声。 为分析噪声类型或噪声组合,根据式(3)计算得到4种不同噪声模型组合的最大似然估计值。表2为山西GNSS基准站时间序列各分量在不同噪声模型的最大似然估计值,数值越大,结果越可靠。仅靠这一指标确定最优模型存在较大片面性,Langbein提出的保守估计方法评价,是以某种噪声模型的最大似然值为参考值,另外几种噪声模型最大似然估计值与参考值作差,差值最大为最优噪声模型[13]。研究中以WN模型下最大似然估计值为参考值,分别将WN+FN、WN+RWN、WN+FN+RWN 3种模型的最大似然值与之作差,得到的结果如第41页图1至图3所示。 图1 N方向最大似然值差值 图2 E方向最大似然值差值 图3 U方向最大似然值差值 表2 山西GNSS基准站最大似然估计值 可以看出,山西省GNSS基准站时间序列各分量的WH+FN、WH+RWN、WH+FN+RWN与WH噪声模型的最大似然估计值之差值大于0,表明各分量中存在白色噪声,同时也存在有色噪声;WH+FN、WH+FN+RWN的噪声模型最大似然估计值差值大于WH+RWN,且这两种模型组合差值彼此极为接近,表明WH+FN、WH+FN+RWN两种噪声模型组合优于WH+RWN。 计算结果显示,山西省GNSS基准站时间序列各分量中,存在WH+FN或WH+FN+RWN噪声模型。根据蒙特卡罗模拟实验证明,WH+FN与WH+FN+RWN两种噪声模型无可分性[14]。因此,根据前人研究结果,以WH+FN+RWN为最佳噪声模型组合,验证噪声模型中各种噪声相对应的噪声分量估值,确定随机漫步噪声是否存在[15]。 第42页表3为山西基准站时间序列WH+FN+RWN噪声分量数值,可以得出,山西省GNSS基准站时间序列各分量具有不同噪声特性。其中,SXCZ、SXCH、SXKL、SXLF、SXLQ站时间序列N方向存在WH+FN类型的噪声,SXDT、SXGX、SXTY、SXXX站时间序列在N方向存在WH+FN+RWN噪声;山西各基准站时间序列E方向存在WH+FN+RWN噪声;SXDT的U方向时间序列存在WH+FN+RWN噪声,其余基准站U方向时间序列包含WH+FN噪声[16-17]。选用WH+FN+RWN为山西 GNSS基准站的最佳模型并不科学。因此,山西省GNSS基准站N方向的时间序列噪声模型为WH+FN或WH+FN+RWN,E方向的为WH+FN+RWN,U方向的为WH+FN。 表3 基准站坐标分量时间序列噪声分量估值 运用CATS软件里谱指数方法、最大似然估计方法分析山西GNSS基准站时间序列中的噪声特征,得到以下结论: (1)应用CATS软件计算山西省基准站坐标时间序列的谱指数,结果表明,基准站N、E、U方向时间序列的噪声分量均具有明显的负谱指数,谱指数值介于-2~0之间,基准站坐标、时间序列不仅包括白色噪声,也包括有色噪声。 (2)采用CATS软件WH+FN、WH+RWN、WH+FN+RWN、FN+RWN四种噪声模型,对山西省基准站时间序列进行最大似然估计值计算,与WN模型的最大似然估计值作差比较,初步判定WN+FN+RWN为最佳噪声模型。 (3)山西省GNSS基准站时间序列在N、E、U方向上具有不同的噪声特性。基准站点在N方向上有5个站点包含WN+FN+RWN噪声,4站点包含WH+FN噪声;E方向上有9个站点包含WH+FN+RWN噪声;U方向上大部分站点只包含WH+FN+RWN噪声,有1个站点包含WH+FN噪声。所以,山西省GNSS基准站时间序列采用WH+FN+RWN模型作为N、E、U方向的最佳噪声模型并不合理,其最佳噪声模型应为:N方向上采用WH+FN+RWN或WH+FN模型,E方向上采用WH+FN模型,U方向上采用WH+FN+RWN模型。可见,三个方向的最佳噪声模型可以不一致。 感谢中国地震台网中心高级工程师李瑜对该文的指导,文章所用数据源于中国地震台网中心和中国地震局GNSS数据产品服务平台。1.3 最大似然估计法
2 噪声计算结果与特征分析
2.1 频谱指数分析结果
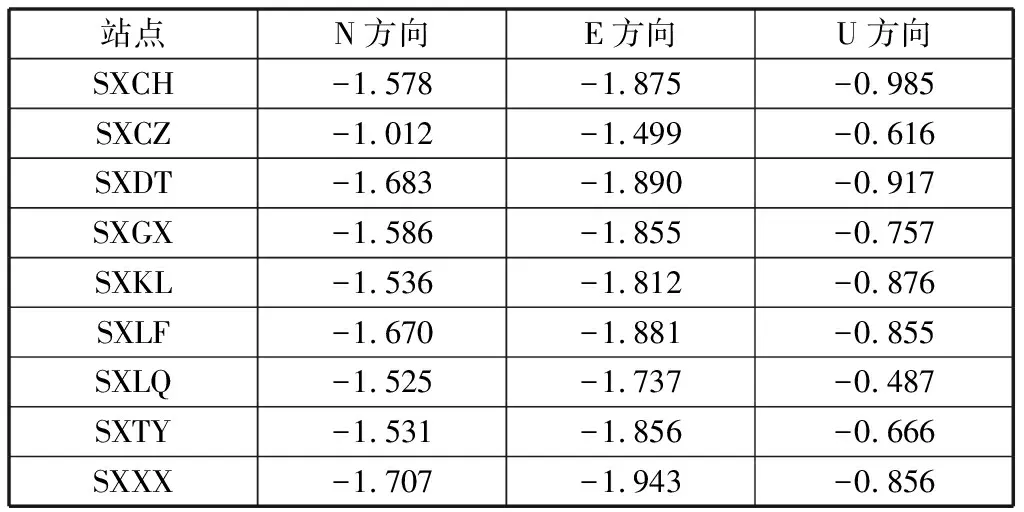
2.2 计算各基准站最大似然估计值
2.3 各基准站最佳噪声模型分析


3 结论与讨论
