服役期迷流影响下不同净距地铁双洞的电位分布特性

刘瑞康,岳 健,朱铁环,安永林

(1.湖南科技大学 土木工程学院,湖南 湘潭 411201; 2.湖南科技大学 机电工程学院,湖南 湘潭 411201)

随着隧道工程的快速发展,隧道工程学科与电学类学科的交叉融合已是大势所趋.不仅应重视隧道在受力、位移与渗透等方面的特性,还应关注隧道的电学特性与腐蚀特性,因为这些特性常常相互耦合发生作用[1].对处于服役期的地铁隧道来说,电力牵引的地铁列车在隧道钢轨上运行时,很可能会产生迷流(杂散电流)并且泄漏到周围环境中,从而对隧道的钢筋混凝土结构与围岩产生电化学腐蚀,因此要对迷流进行防护.隧道产生电化学腐蚀的原因是电位差超过某一规定值.因此想要有效防护迷流,首先应弄清楚迷流影响下隧道的电位分布特性.一方面,以往研究主要关注单洞隧道的电位分布特性,而双洞隧道(如分岔隧道)要考虑相邻两个洞电场之间的相互影响,其电位分布比单洞隧道复杂,目前关于迷流影响下地铁双洞电位分布特性的研究成果还很少见.另一方面,在确定地铁隧道双洞之间的合理净距时,大多只关注双洞应力场的相互影响,较少关注双洞渗流场的相互影响,几乎没有考虑双洞电场的相互影响[2～9].鉴于此,本文以采用盾构法修建的相邻双洞水平平行布置的某段地铁隧道为原型,针对8 种不同的双洞净距,研究服役期迷流影响下地铁双洞的电位分布特性.这不仅对于确定迷流的危害程度与防护措施具有重要的参考意义,也可为确定地铁隧道双洞之间的合理净距提供有益的参考.由于要考虑相邻双洞电场在三维空间上的相互影响,解析计算很难达到目的,开展试验的代价又非常昂贵,因此本文通过三维数值模拟进行研究.

1 工程概况与数值模型建立

选取某地铁区间隧段为工程原型,该段隧道的埋深约为12m,分为左右两洞,两洞水平平行布置.运用COMSOL 有限元软件建立研究区段的三维电学数值模型,模型整体宽为200m,高为100m,纵向长度取990m(代表机车取流点到牵引变电站回流点的距离),模型整体的网格划分如图1所示(仅显示一部分).整个模型共约60 万个单元,每个洞的横断面均为圆形.管片环的外径为6.2m,内径为5.5m,管片衬砌厚度为0.35m,管片环宽1.5 m.全环管片分6块,标准左环由一个封顶块(KT),两个邻接块(B1T、B2T)和三个标准块(A1TL、A2TL、A3TL)组成;标准右环由一个封顶块(KT),两个邻接块(B1T、B2T)和三个标准块(A1TR、A2TR、A3TR)组成.两洞关于中夹岩中线对称布置,其中左洞横断面布置如图2所示.

图1 模型整体的网格划分

图2 左洞横断面

以往的电学数值模型基本上将一环管片衬砌笼统地当做一个圆环来模拟,划分单元时没有明确区分各种管片,而对不同类型的管片进行区分建模是本文所建模型的一个特点.如图3和图4所示,在各洞管片中,封顶块划分为2 个单元,每一个邻接块划分为6 个单元,每一个标准块也划分为6 个单元,各块管片之间有明确的界限,方便确定电腐蚀风险最大的管片位置.材料的计算参数见表1,所有材料都采用三维实体建模,其中单根钢轨等效成0.06m × 0.06m × 990m 的实体模型.

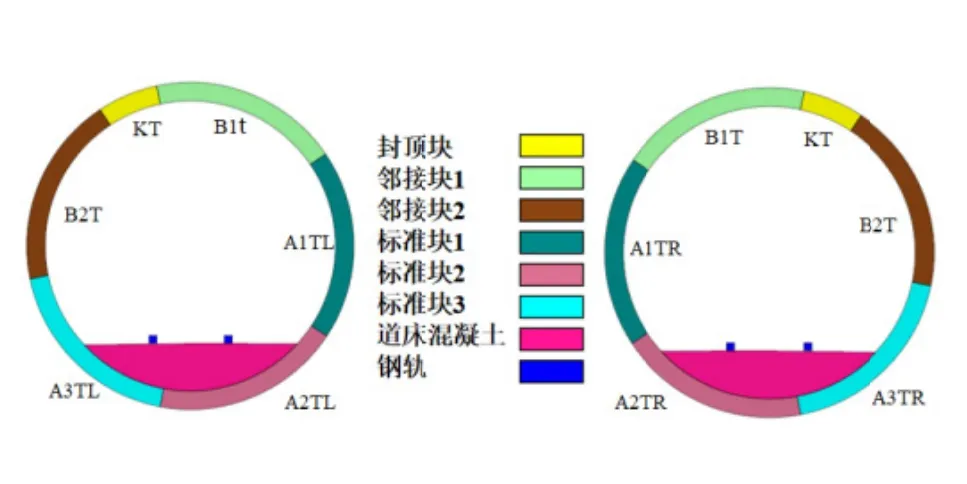
图3 隧道结构布置

图4 洞室周边的网格划分

表1 材料的计算参数

迷流在介质中的分布遵循欧姆定律和电流守恒定律,其本构方程为

其中Jx、Jy和Jz分别表示x、y和z方向上的电流密度分量,单位为A/m2;ρx、ρy和ρz分别表示x、y和z方向上的电阻率,单位为Ω·m;φ表示电位,单位为V.

在x、y和z方向上电流的连续性方程为

将式(1)代入式(2)可得地铁迷流场基本方程

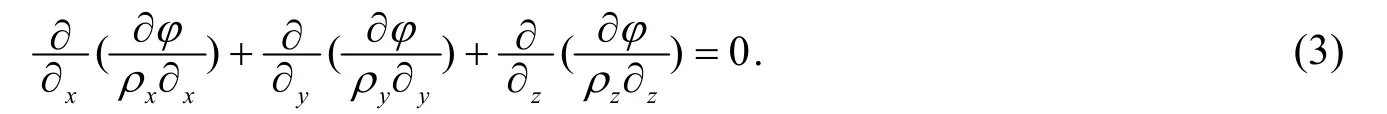
因模型足够大,定义模型底面为接地边界条件,电位为零,其余表面都设置为电气绝缘[10].此处列车取流电流为3000 A,其中绝大部分经由走行轨返回牵引变电所,只有30 A(列车取流电流的1%)作为迷流泄漏到周围环境中,因此在各洞的每一根钢轨的一端均加载30 A 电流.双洞之间的净距分别取为0.5B、1B、1.5B、2 B、2.5 B、3B、3.5 B 和4 B(B 为单洞地铁盾构管片外径尺寸,B = 6.2m),共8 种不同净距工况.

2 数值模拟结果分析

数值模拟结果表明,不同双洞净距下的电位分布规律基本一致,只是电位的数值发生了变化.因此以双洞净距0.5B(图5)和4B(图6)工况为例分析电位分布规律:(1)双洞均为泄漏迷流的钢轨位置的电位最高,电位从泄漏迷流的位置向四周非线性衰减;(2)双洞之间净距为0.5B时的道床混凝土电位在20.7～ 48.4 V 之间,双洞之间净距为4B 时的道床混凝土电位在17.8～ 45.6 V 之间.可见位于钢轨之下的道床混凝土的电位较高,是发生腐蚀的重灾区.这是因为从钢轨泄漏的迷流,首先流入道床混凝土结构并产生电场,所以该部位最易受到迷流的电腐蚀影响.建议道床混凝土采用高绝缘性混凝土,道床以下的管片接缝比道床以上的管片接缝多加一道弹性密封垫进行防水,降低地下水进入道床的概率,从而降低道床混凝土的导电性能.

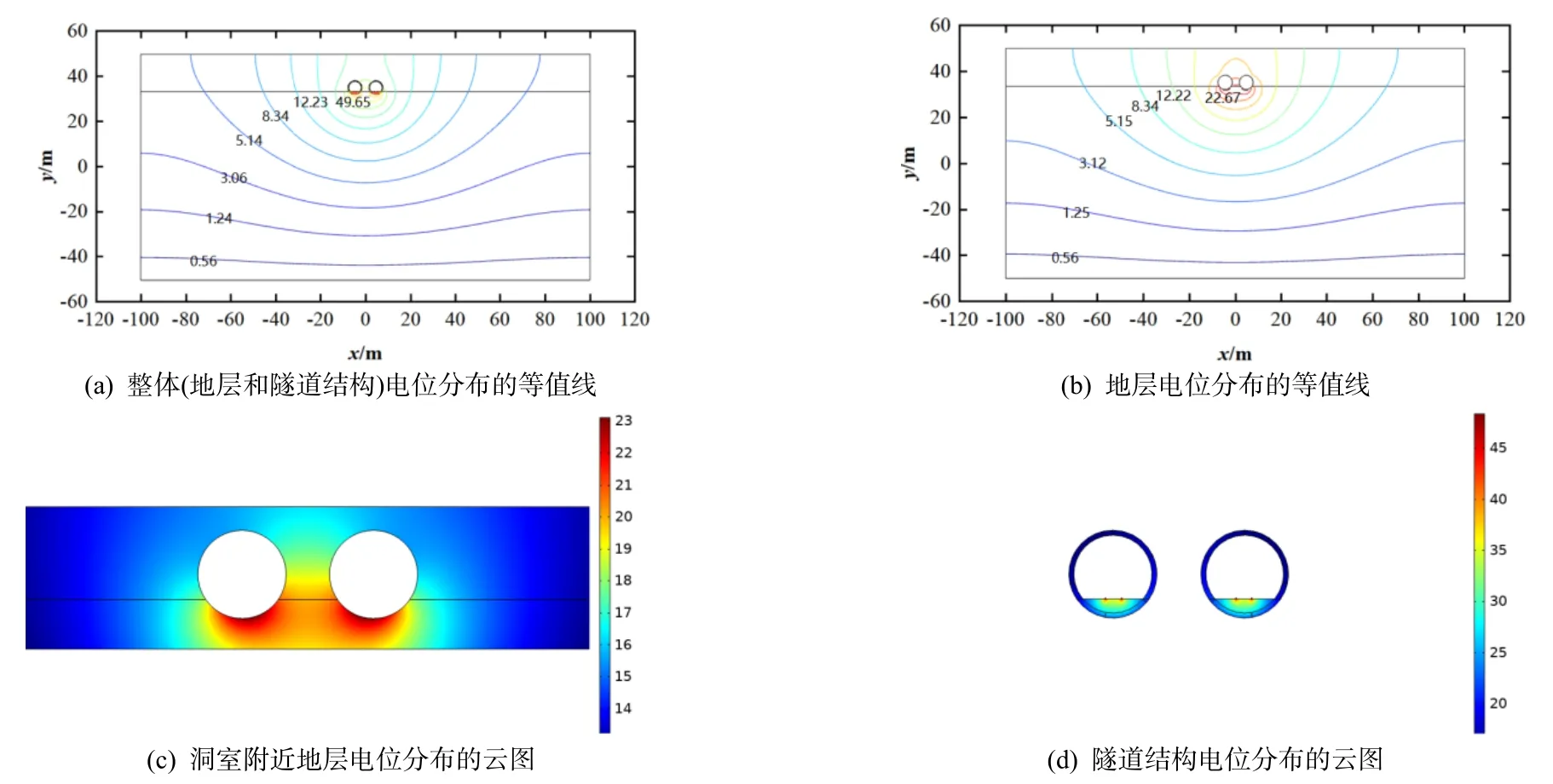
图5 双洞之间净距为0.5B时对应的电位分布

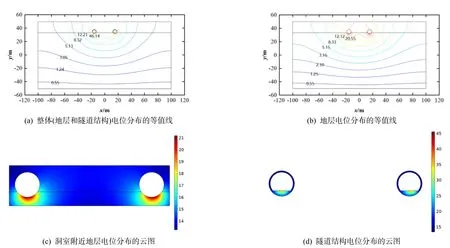
图6 双洞之间净距为4 B时对应的电位分布

图7给出了不同净距下电位沿参考线(道床混凝土顶面的高程线)的变化曲线,由于双洞的轨底电位关于中夹岩中线对称分布,因此仅给出了左洞轨底电位随净距的变化曲线(图8).分析可知:(1)各种净距下,中夹岩中线左右各20 m 范围内的电位变化都相对剧烈,存在明显的双洞电场叠加效应,但随着双洞间净距的增大,双洞之间的叠加效应逐渐减弱.(2)双洞泄漏迷流时,各种净距下都是靠近中夹岩的轨底电位比远离中夹岩的轨底电位高,但是二者的差值基本上不随净距的变化而变化,差值基本保持为0.3 V.(3)以2B净距为界,从2B净距减小到0.5B净距,靠近中夹岩侧的轨底电位增大了2.71V,远离中夹岩侧的轨底电位增大了2.61 V;从2B净距增大到4B净距,靠近中夹岩侧的轨底电位减小了0.28 V,远离中夹岩侧的轨底电位减小了0.22V.由此可见,当双洞隧道泄漏迷流时,以2B净距为界,当净距小于2B时,随着净距的减小,轨底电位急剧增大;当净距大于2B时,随着净距的增大,轨底电位变化相对较小.这一点对于确定双洞合理净距具有重要的参考意义.

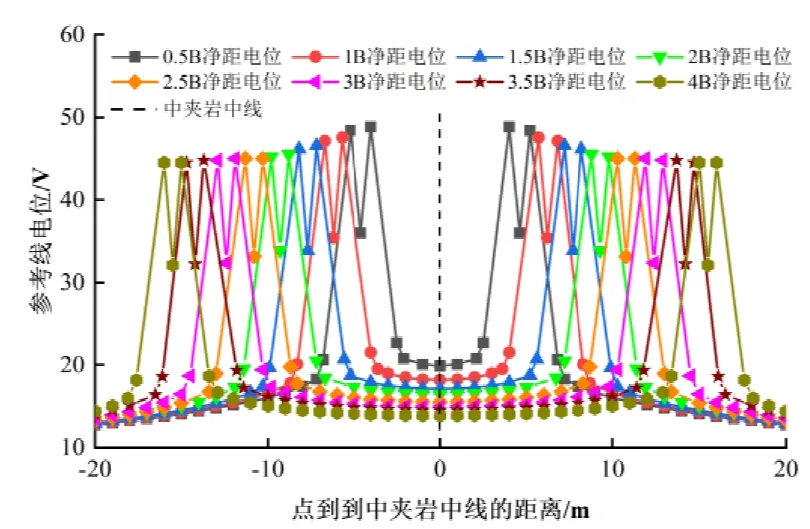
图7 八种净距电位沿参考线的变化曲线

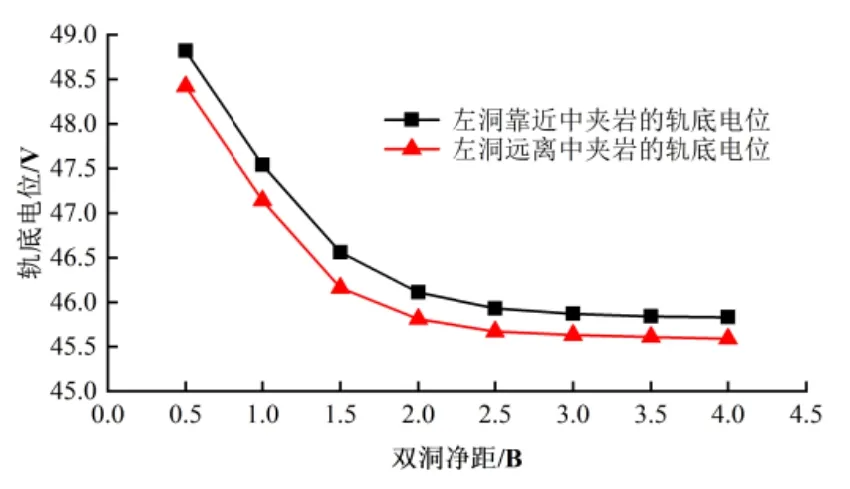
图8 左洞轨底电位随净距的变化曲线

双洞电位沿中夹岩的竖直中线对称分布,图9为双洞之间不同净距的管片内外侧电位的分块示意.分析可知:双洞之间净距为0.5B 时,对于各洞的一环管片,其中封顶块(KT)的电位最小,在16.97 ～ 17.62 V 之间,靠近中夹岩的标准块(A2TL、A2TR)的电位最大,在20.99～22.73V 之间;双洞之间净距为4 B 时,对于各洞的一环管片,其中封顶块(KT)的电位最小,在14.37 ～ 15.00 V 之间,靠近中夹岩的标准块(A2TL、A2TR)的电位最大,在16.62 ～ 18.36V 之间.由此可知,尽管双洞之间的净距发生了变化,但对于各洞的一环管片,封顶块(KT)的电位都为最小,标准块(A2TL或A2TR)的电位都为最大,因此这一块管片的电腐蚀风险最大.

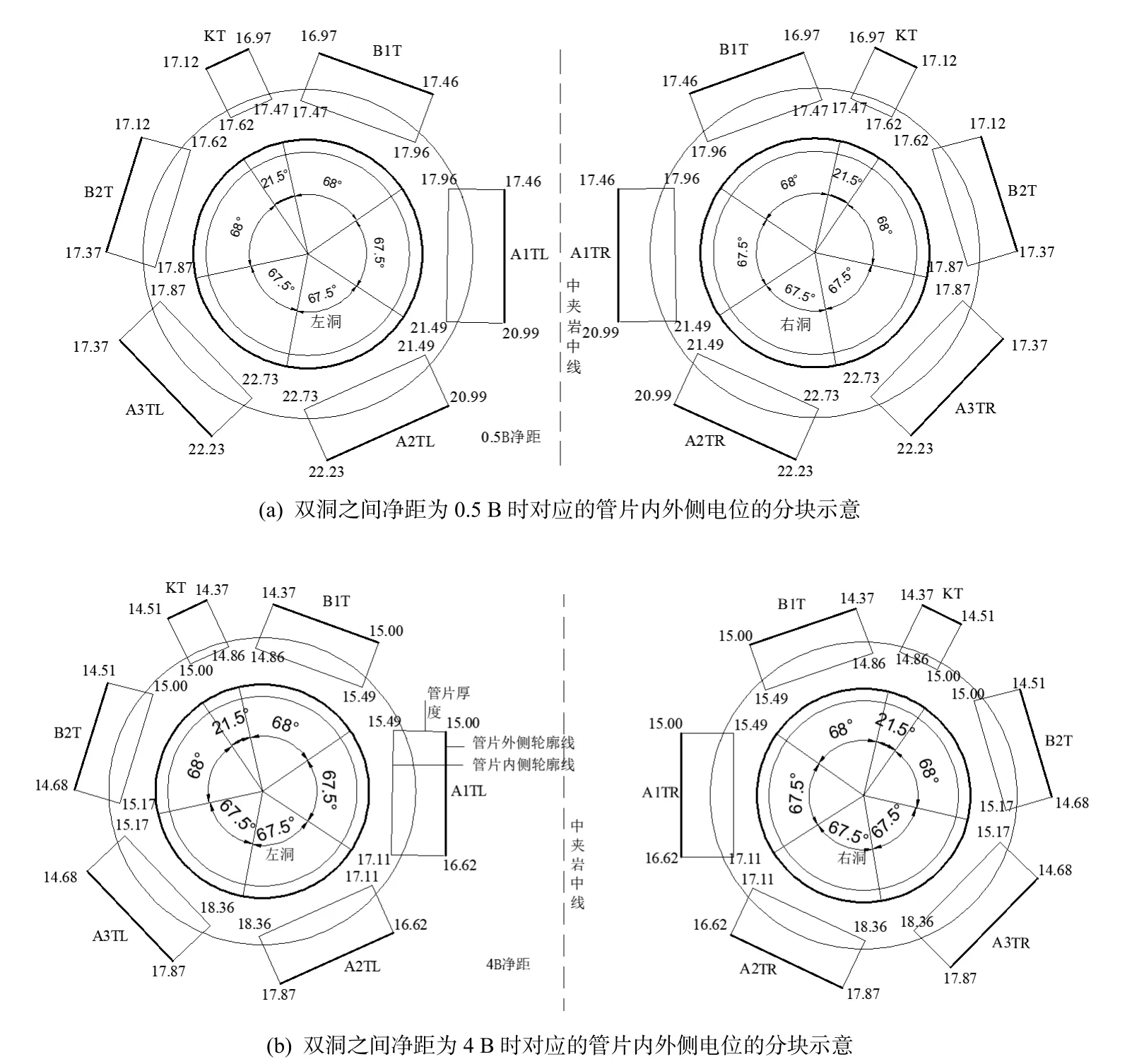
图9 不同净距的管片电位分块示意(单位: V)

从图9 可明显看出,管片内侧与外侧的电位沿环向的分布规律类似,接下来以管片内侧电位为例进行分析.由于双洞的电位关于中夹岩中线呈现对称分布,故图10 只给出了左洞管片内侧电位的变化曲线.分析可知: (1)在不同净距下,左洞管片电位均呈现下半部电位高于上半部电位; 管片全环的最高电位均出现在拱底,其中双洞之间净距为0.5 B 时对应的内侧电位最大,为23 V; 管片全环的最低电位均出现在远离中夹岩边墙处,其中双洞之间净距为4 B 时对应的内侧电位最小,为15.44 V; (2)双洞之间净距从0.5 B 增大到2 B 时,左洞管片拱顶内侧的电位减小了1.95 V,双洞之间净距从2 B 增大到4 B 时,左洞管片拱顶内侧的电位减小了0.60 V; 左洞管片下半部的电位呈现为“上凸型”的曲线分布,随着净距减小,凸点向中夹岩方向偏移.双洞之间净距从0.5 B 增大到2 B 时,左洞管片拱底内侧的电位减小了3.60 V,双洞之间净距从2 B增大到4 B 时,左洞管片拱底内侧的电位减小了0.68 V; (3)针对管片存在的电腐蚀风险,建议加强管片自身钢筋混凝土的抗渗性和绝缘性,如掺加硅粉降低水泥用量或者在管片的迎水面喷涂防水层等.

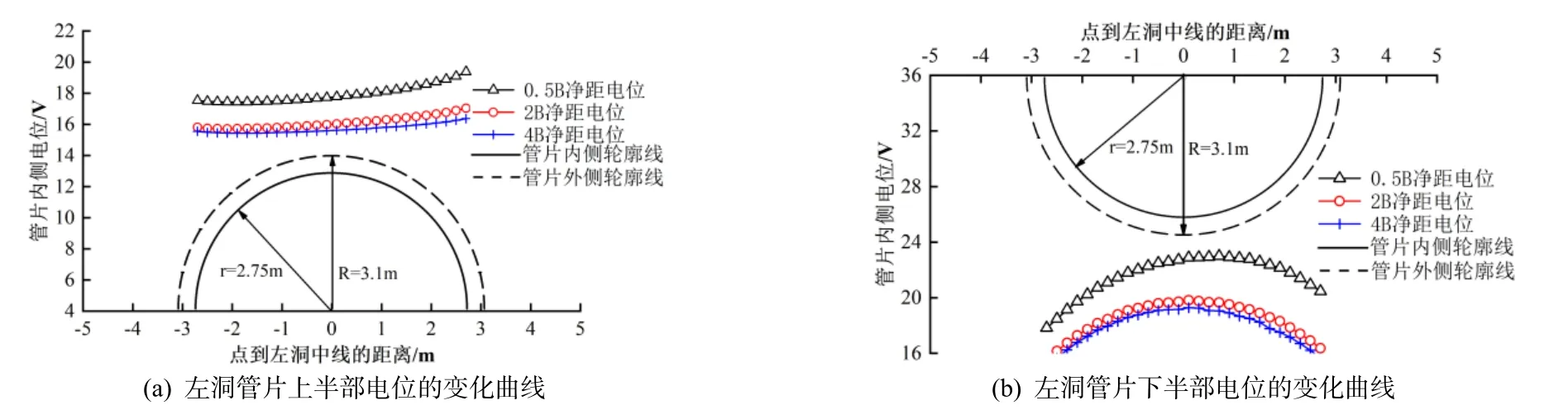
图10 双洞管片的电位变化曲线

3 结束语

对于双洞净距在0.5 B ～4 B 之间的地铁隧道,当双洞泄漏迷流时,位于钢轨之下的道床混凝土的电位较高,是发生电腐蚀的重灾区; 各种净距下靠近中夹岩的轨底电位都比远离中夹岩的轨底电位高,但是二者的差值基本上不随净距发生变化; 管片全环的最高电位出现在拱底,最低电位出现在远离中夹岩边墙处; 在一环管片中,靠近中间岩拱脚处的标准块的电位最大,这一块管片的电腐蚀风险最大.

当双洞之间的净距小于2 B 时,随着净距的减小,轨底电位急剧增大; 当双洞之间的净距大于2 B 时,随着净距的增大,轨底电位变化相对较小.针对本文的工程情况,从迷流影响下双洞电场的相互影响与节约用地这两个方面考虑,建议双洞之间的净距不要超过2 B,当然具体净距的选择还应考虑双洞的受力性状.

建议道床混凝土采用高绝缘性混凝土,道床以下的管片接缝比道床以上的管片接缝多加一道弹性密封垫进行防水,从而降低道床混凝土的导电性能; 针对管片存在的电腐蚀风险,建议加强管片自身钢筋混凝土的抗渗性和绝缘性,如掺加硅粉降低水泥用量或者在管片的迎水面喷涂防水层等.