基于三维重构的哈蜜瓜均瓣雕花算法

赵明岩，林 敏，徐 鹏，王勇金，宋天月，梁明轩，胡剑虹

·农产品加工工程·

基于三维重构的哈蜜瓜均瓣雕花算法

赵明岩1，林 敏1，徐 鹏2※，王勇金1，宋天月1，梁明轩1，胡剑虹1

（1. 中国计量大学机电工程学院，杭州 310018； 2. 中国计量大学理学院，杭州 310018）

为解决哈密瓜雕刻速度慢、花瓣大小不一致等问题，该研究提出了一种基于三维重构的哈蜜瓜均瓣雕花算法。对多角度拍摄得到的哈蜜瓜照片进行滤波处理，提取其图像特征并进行稀疏重建，通过点云坐标得出哈蜜瓜的特征参数；接着在稀疏点的基础上利用CMVS/PMVS算法进行稠密重建；最后调节八叉树算法与泊松表面重建，得到哈密瓜精确三维空间坐标。根据哈密瓜体型特征及设定花瓣数量，将点云三角网格化在深度优先算法的基础上结合粒子群算法，规划雕刻起点、终点及雕刻深度，使每个花瓣体积相同。采用48个哈密瓜，雕刻花瓣数取15～30，雕刻深度为1.5、2.0、2.5 cm。其中切割花瓣数为28这一组精度最低，测得最大与最小花瓣体积分别为3.40与3.25 cm3，最大体积差为0.15 cm3，误差小于5%。结果表明，该研究提出的基于三维重构的哈蜜瓜均瓣雕花算法精度高，研究结果可为机器人雕刻哈密瓜提供技术支持。

图像处理；粒子群算法；三维重构；均瓣雕花；点云拼接；三角网格化

0 引 言

自动化是餐饮行业发展的必然趋势。炒菜机器人[1-2]、送餐机器人[3-4]等已能够部分取代人工，极大提高了工作效率。对于蔬果雕花作业，目前仍然依靠人工手工雕刻，不仅费时费力，且存在安全隐患，人口老龄化及人工成本的日益增加使雕花熟练工的缺口越来越大。随着生活水平的提高及餐饮智能化时代的到来，研制蔬果雕花机器人也刻不容缓。尤其对结构虽然繁杂但具有一定规律的花型，机器人雕花具有巨大的优势。然而雕刻对象的大小、形状、品种往往不完全一致，因此在实施雕刻之前，必须对雕刻对象进行三维重构[5-8]，以获得精确的三维空间坐标[9]，从而规划执行终端的雕刻路径。

哈密瓜是一种常见的水果，常常被雕刻成花篮，盛放果肉、高档菜品等。当哈密瓜每个花瓣的体积完全相等时，视觉效果最好。由于哈密瓜外形（以及去籽后的内部）并非精确的轴对称形状，因此人工雕刻时，很难做到每瓣体积完全相同。如果对哈密瓜进行三维重构，得到哈密瓜外形（以及去籽后的内部）的精确尺寸（空间坐标点），就能规划机器人的雕刻路径，从而实现预期效果。

澳大利亚的Lehnert等[10]设计了收割机器人Harvey，将机器人视觉技术和作物操作工具相结合，利用三维重构技术通过点云颜色的突变来检测甜椒临界削根位置，对目标甜椒花梗进行定位，确定花梗的质心，成功率达76.5%。郭彩玲等[11]使用三维激光扫描仪提出了基于靶球的KD-trees-ICP算法，用于高精度配准苹果树冠层三维点云数据，得到高于人工测量精度的枝干、果实、叶片参数，相对误差小于5%。柴宏红等[12]基于甜菜多视角图像序列构建甜菜根的三维点云模型，较为准确提取了甜菜最大直径、根长、顶投影面积、紧凑度、突起率等10个表型参数，初步建立了产糖量与表型参数的关系。孔彦龙等[13]基于图像综合特征提取，得到马铃薯周长和面积，进而将马铃薯分选为圆形、椭圆形、畸形三类，分选准确率达96%。吴丹等[14]通过轮廓投影方法重建水稻三维可视外壳点云模型，并利用反投影方法进行点云着色，提取水稻更为全面的性状参数，但伴有误匹配。Hui等[15]基于稠密重建（Multiple View Stereo，MVS）方法从黄瓜、辣椒、茄子的图重建三维点云，提取和评价了植物结构的表型参数。Mortensen等[16]通过莴苣的彩色三维点云分割，提取体积、表面积、叶面积的高度预测因子，并将鲜质量进行分析，得到较高预测精度（1值范围0.88～0.91）。从以上分析可知三维重构技术应用广泛，可测得大小、形状不一的多种不规则对象的各项表型参数。但上述研究方法尚有不足之处，如提取三维点云数量少、精度低、耗时长，相关仪器费用高、操作繁琐等，且鲜有关于利用三维重构结果进行机器人路径规划的研究。

本文提出了基于三维重构的哈密瓜均瓣雕花算法并应用于机器人实现。获取全面的三维层面表型信息后，在粒子群算法的辅助下[17]，实现高精度雕花，为哈密瓜（或其他蔬果）三维几何重建、机器人雕花提供技术支持。

1 哈密瓜的三维重构

1.1 机器视觉光源设计

为精确获取欲雕花对象轮廓，采用双摄像头并行拍摄。为减少左右摄像头的相互干扰，在暗室光源的选择上采用条状白光LED。将两条功率为9.6 W的条状LED安装在蔬果雕花装置中左右摄像头的旁侧，暗室内侧作白色喷漆处理，通过光源的漫反射，可使待检测区域达到检测的光学环境[18]要求且无阴影。

1.2 图像获取

另将主摄像头固定在机械臂上，调整主摄像头使相机光轴方向在水平方向上[19]。其中摄像头使用固定光圈拍摄，拍摄时尽可能绕光心旋转，相邻照片应有一定重叠部分使最终的3D点云尽可能密集、光顺。

调整摄像头的高度，使摄像头以30°俯视角对哈密瓜进行拍摄，哈密瓜在托盘作用下匀速旋转（转速为4 r/min），托盘每转动3°摄像头拍摄一张图片，哈密瓜旋转一周后，获得一组序列图像；再次调整摄像头高度，使得摄像头以30°仰视角对哈密瓜进行拍摄，哈密瓜每转动3°摄像头拍摄一张图像，获得一组序列图像，如图1所示。

通过多角度拍摄获得多视图后，根据运动结构算法（Structure From Motion，SFM）得到相机位置[20]，采用尺度不变特征变换算法（Scale-Invariant Feature Transform，SIFT）提取图像中特征点的局部特征[21]，在尺度空间中寻找极值点，然后使用高斯差分算子建立图像的多尺度表示，确定特征点的位置、尺度和方向参数，并产生图像描述符。

用Kd-tree模型[22]计算两两图片相应特征点之间的欧氏距离，进行特征点的匹配，找到特征点匹配个数达到要求的图像对，计算对极几何，估计矩阵并通过随机抽样一致算法（Random Sample Consensus，RANSAC）优化改善匹配对[23]，若特征点能在匹配对中链式传递，便能形成相机轨迹。

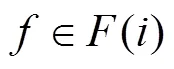
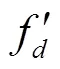
在算法中采用Kd-tree的数据结构计算最邻匹配，当距离在设定的预知范围内时即判定为可接受的匹配对，针对特征点不一定能一一对应的问题，采用去除重复特征点匹配对的算法来解决。对于初选匹配对仍有可能不可靠的情况，如匹配到的特征点在实际场景中不符合物理规律等，引入几何约束来检测。通过计算对极几何，矩阵将匹配对图像中的像素坐标联系起来，其中包含相机的内参信息，增加符合实际匹配对的像素坐标均需满足：

[1][1]T=0 （2）

式中[1]、[1]为匹配对像素坐标。

用RANSAC算法将矩阵计算出的噪声数据滤去，即可确定所有匹配对将匹配对之间出现的共同特征点相连形成轨迹，根据轨迹构造图像连接图，连接图包含每个图像的节点并有着共同的轨迹边缘。三维重构算法流程如图2所示。

1.3 点云处理

1.3.1 平面检测

通过随机抽样最大似然估计算法（Maximum Likelihood Estimation by Sample and Consensus，MLESAC）对3D点云进行平面检测[24]，采用最大似然估计将问题转化成求解代价函数的最小值问题，代价函数公式为：

用归一化8点算法获得基本矩阵，计算原始数据中每对匹配点之间的距离d[25]，其中

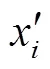
1.3.2点云旋转及点云降噪

由于拍摄角度变化等原因，重构出的哈密瓜3D点云图容易呈现倾斜姿态，因此需要对其姿态进行校正。

通过平面检测，确定蔬果所在平面，以该平面为标准，采用三维放射变换矩阵M对整个点云进行旋转并缩放，最后，对处理过的点云进行降噪。点云拼接过程如图3所示，点云旋转矩阵为：

将处理完成的点云坐标导出，共计927 094个点，可见点云数据能够详尽描述哈密瓜的各个特征。

1.4 曲面重构

根据相机的内部参数与外部参数，以及个视角下得到的条轨迹[26]，能对哈密瓜的空间构型实现基本的还原。为解决二维图像到三维立体构型过程存在的投影误差问题，引入光束平差法（Bundle Adjustment, BA）对三维重建进行优化[27]。

式中为3D点个数，为拍摄场景个数，v为第个3D点在第个场景上的映射，(a,b)为点在场景的预测投影，x为第个3D点在第个场景中的实际坐标，(,)为向量，的欧式距离。

首先选择有足够多匹配点、有足够远离相机中心的初始化匹配对，用5点法估计初始化匹配对的外部参数，然后利用轨迹三角化提供初始化的3D点，对初始化的两帧图像进行第一次BA。随后不断增加新的图片和3D点进行BA，直到剩下的图片观察到的特征点不超过20为止，结束BA。由此可以得到哈密瓜在空间中的稀疏3D点云，在稀疏点的基础上利用集群多视角立体视觉算法（Cluster Multi-view Stereo, CMVS）和基于面片的三维多视角立体视觉算法（Patch-based Multi-view Stereo，PMVS）进行稠密重建，调节八叉树深度控制细节精度，再进行泊松表面重建，修复流型边缘，最后进行参数化和纹理投影得到重构后的哈密瓜，即三维重构完成，如图4所示。

2 均瓣雕花算法

2.1 哈密瓜点云三角网的构建

在重构过程中，密瓜由927 094个点云拼接而成，在众多点云中以任意一点为基准寻找距离该点最近的两个点形成初始三角形，再以三角形的三条边为基准线继续向外拓展三角形，直至所有点云都被包含于该哈密瓜空间立体三角网模型中，如图5a所示。

待点云三角网格化完成后，将空间立体三角网投影到坐标轴的面。设坐标(1,1,1)，(2,2,2)，(3,3,3)，1(4,4,0)，1(5,5,0)，1(6,6,0)，如图5b所示。

通过海伦公式计算投影三角形面积，以投影后3个点坐标的平均值作为高，进而计算得到三棱锥体积。

三角形各边长分别为：

式中1、2、3为三角形三边边长，cm。

Δ111周长的一半为：

式中为三角形周长的一半，cm。

Δ111面积为：

式中为三角形面积，cm2。

三棱锥的高为：

式中为三棱锥的高，cm。

三棱锥的体积为：

式中为三棱锥的体积，cm3。

2.2 哈密瓜点云搜寻算法

重复的二维平面图形可重构出哈密瓜的点云模型，通过视觉处理识别深度、颜色、轮廓等特征，从而进行布点。

2.2.1 获取哈密瓜表型参数

图6为上位机重构得到的三维哈密瓜正视图，选取该目标拟合出一个外接矩形，需要事先定义一个比率来测量每个给定度量单位的像素数pixels_per_metric（比率指标）。为了确定被雕刻哈密瓜的实际高度，需要使用一个参照物作为校准线，通过比率指标可求出矩形最上条边与校准线的实际高度，将实际高度传送给机械臂，实际高度对应的就是机械臂轴的值。

2.2.2 俯视角度计算下刀口密度与轴及轴机械坐标

在上位机的俯视图中，通过OpenCV函数引用cv2类的轮廓周长变量得到哈密瓜周长数据[28]：

perimeter = cv2.arcLength(cnt,True) （13）

式中perimeter为轮廓周长，cv2.arcLength()为计算轮廓周长的函数。

假设计算得到哈密瓜周长为68 cm，在其轮廓上均匀地取34个点记为预起点，这样相邻点之间的弧长为68/34=2.0 cm，再将这34个点与哈密瓜内核圆心相连接，连接线与内核轮廓的34个交点记为走刀路径的预终点。这34个预终点与之前的34个预起点就会形成34段预雕刻路径，如图7所示。

哈密瓜形态不同，重构结果也不同，为使雕刻效果最好，应使雕刻后每一瓣果肉体积相同。首先，确定哈密瓜切削高度与深度，保留该高度与深度下的密瓜点云，剔除其他点云的坐标信息；然后，根据密瓜最外圈点云拟合出圆弧函数确定圆心，将360°除以雕刻瓣数确定雕刻预起点、预雕刻终点、预雕刻路径；而后以每一瓣花瓣体积相等为目标函数，以每一瓣花瓣切削深度相等、切削角度相等为限制条件，在深度优先算法[29]的基础上结合粒子群算法，通过不断地递归迭代在密瓜点云坐标中找到较优解；最后将找到的较优点云坐标储存为新的数据集，上位机调用数据集中的点云坐标控制机械臂走刀，对哈密瓜进行雕刻。雕刻刀切割次数取决于取点的个数，可由用户自定义设置。

2.3 基于三维重构的哈密瓜布点

对于复杂的三维模型，可在已知三维重构点云的基础上通过算法获得。在哈密瓜外侧标记出新数据集中的点云坐标。

图8中，轮廓1为刀具的定位圆，半径为（+2 mm），2 mm的半径差保证了在每次切入时刀具不会误触蜜瓜侧面；轮廓2为待雕刻蜜瓜的最小外接圆，半径为(mm)；轮廓3起到了确定雕刻深度的作用，不仅保证了花瓣的整齐，也能保证切断余料。姿势点1为定位点，姿势点2为切入点，姿势点3为退刀点。

在每个花瓣的雕刻过程中，姿势点1、2、3共线。刀具先移动到姿势点1调整到合适的姿态角后从姿势点2切入，接着沿刀具的刀脊运动一定深度到姿势点3并退刀至姿势点1，然后刀具沿着哈密瓜的外侧运动至下一个相邻的姿势点1，重复上述过程，完成哈密瓜的整体雕刻。雕刻机器人为纳智（NACHI）MZ04-01-CFD-0000的6自由度机器人。雕刻装置采用特殊的刀具，集合了雕刻圆刀，玉婉刀以及锯齿刀，刀具送行速度可达8.03 rad/s，雕刻时刀具与水平面夹角维持在60°，切割深度为设定值，如图9所示。

2.4 误差分析

雕刻完成后，每个花瓣的体积均相同，达到最佳视觉效果。为验证该算法的精确度，分别通过计算规则及不规则模型的体积进行试验验证，构建正方体、三棱锥、半球模型。通过坐标点信息可以计算出正方体、三棱锥、半球的体积与表面积值。为进一步验证算法的可行性，计算得到不规则石块、哈密瓜体积后，再用排水法测得其对应体积。为了计算模型体积，在构建的模型上提取点云数据，构造空间Delaunay三角网[30]，将构建的空间三角网中的每个三角形投影到面，计算出投影三角形的面积与3个顶点纵坐标的平均值后，相乘得到三棱锥体积，将所有三棱锥体积累加即可得到模型总体积。各模型计算值与实测值的对比如表1所示。

由测试结果可知，对于正方体、三棱锥模型的体积、表面积，计算值与实测值一致，绝对误差为0；对于半球模型的体积和表面积，计算值与实测值误差小于0.02%，只有十分微小的偏差。由此可知该方法用于规则模型的体积与表面积计算是可行的。对于不规则的石块、哈密瓜，通过点云三角网重建计算得到的体积与实测体积误差小于5%。

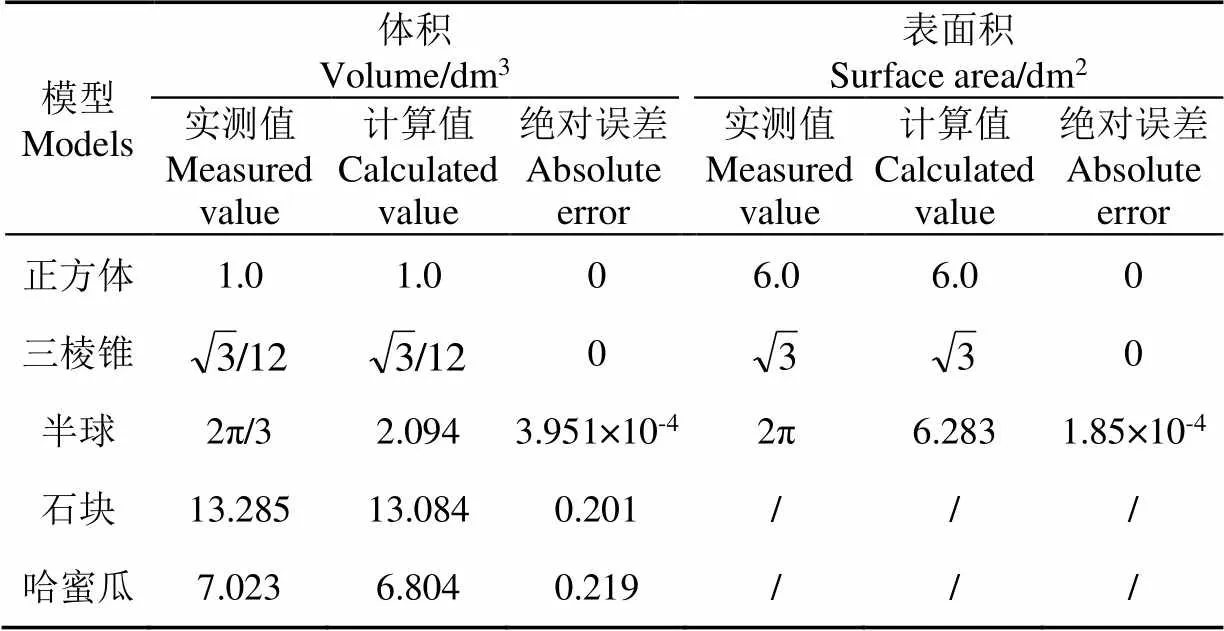
表1 不同形状模型计算值与实测值对比

基于多视角拍摄图片重建的哈密瓜三维模型包含其相应的颜色、纹理、几何尺寸等信息，并可根据三维点云提取哈密瓜的各种表型参数。为验证拟合后哈密瓜横截面轮廓精度，提取哈密瓜不同高度所对应的最大直径参数，其计算值与实测值对比如表2所示。

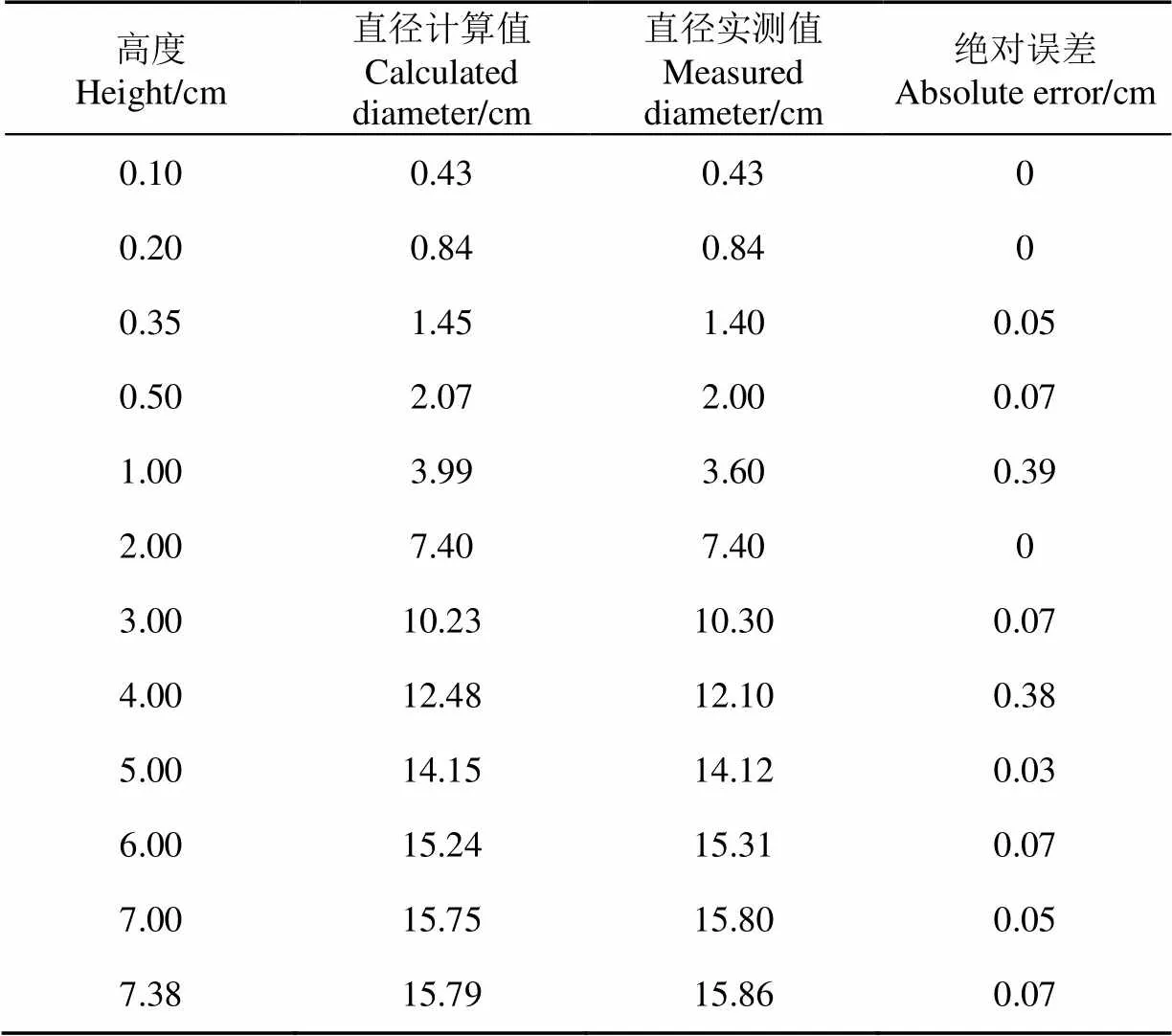
表2 哈密瓜直径计算值与实测值对比

通过以上数据可知，高度为7.38 cm的哈密瓜，其最大直径为15.79 cm；直径实际测量值与计算值的最大误差值为0.39 cm，不同高度的哈密瓜直径测量值与其计算值基本吻合。

进一步验证雕刻后哈密瓜花瓣的每一瓣体积是否相等。试验样本数量为48个哈密瓜，每3个哈密瓜分为一组，雕刻花瓣数取15～30，雕刻深度取1.5、2.0、2.5 cm，结果如表3所示。

对各个哈密瓜雕花模型进行重构雕花验证，其中切割花瓣数=28这一组精度最低，哈密瓜花瓣体积的实际测量值与计算值如图10所示。

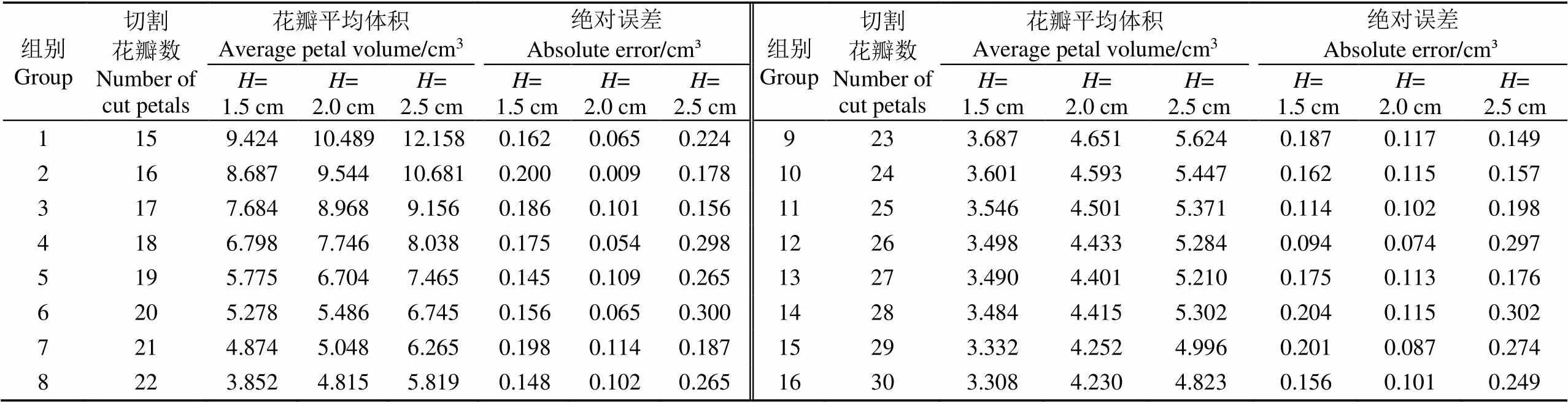
表3 哈密瓜组间花瓣平均体积的差异统计

注：绝对误差为花瓣平均体积与花瓣理论体积之差；为雕刻深度。

Note: The absolute error is the difference between the average volume of petals and the theoretical volume of petals.is the engraving depth.

由图10可知28瓣哈密瓜花瓣体积实测值分布在计算值的上下两侧。根据试验数据可知雕刻深度=1.5 cm时，最大花瓣体积为3.40 cm3，最小花瓣体积为3.25 cm3，花瓣体积差值的最大值仅为0.15 cm3；雕刻深度=2.0 cm时，最大花瓣体积为4.37cm³，最小花瓣体积为4.25 cm3，花瓣体积差值的最大值仅为0.12 cm3；雕刻深度=2.5 cm时，最大花瓣体积为5.06 cm3，最小花瓣体积为4.95 cm3，花瓣体积差值的最大值仅为0.11 cm3；误差小于5%，视觉效果较好。

3 结 论

1）建立了哈密瓜的点云模型，对多角度拍摄得到的哈蜜瓜照片进行滤波处理，提取其图像特征并进行稀疏重建，接着在稀疏点的基础上利用CMVS/PMVS算法进行稠密重建，得到哈密瓜点云的坐标；

2）提出了哈密瓜均瓣雕花算法，通过Delaunay三角网将点云三角化，将单个计算得到的三棱锥体积累加，在各花瓣体积相等的目标函数及多个约束条件下辅以粒子群算法，最终得到机器人雕刻路线；

3）将均瓣雕花算法应用于计算正方体、三棱锥、半球体等模型，体积误差最大值不超过0.02%；应用于石块、哈密瓜等不规则体误差最大值不超过5%；

4）本文提出了一种基于三维重构的哈蜜瓜均瓣雕花算法，除了准对称回转体，也可用于其他非均匀对称几何模型体积、表面积的求解以及形态特征参数的提取，适用于智慧餐厅、智慧农业领域。

[1] 杜险峰，张培茵，芦健萍. 烹饪机器人创新实验平台开发[J]. 对外经贸，2018(1)：136-138.

Du Xianfeng, Zhang Peiyin, Lu Jianping. Development of innovative experimental platform for cooking robot[J]. Foreign Economic Relations & Trade, 2018(1): 136-138. (in Chinese with English abstract)

[2] 邓威，杨淋晖，刘唯. 智慧餐厅炒菜机器人工业设计实践研究[J]. 产业科技创新，2020，2(19)：61-62.

Deng Wei, Yang Linhui, Liu Wei. Industrial design and practice of intelligent restaurant cooking robot[J]. Industrial Technology Innovation, 2020, 2(19): 61-62. (in Chinese with English abstract)

[3] 黄云峰. 基于E-puck机器人自主巡线智能小车的餐厅送餐系统设计[J]. 自动化与仪器仪表，2020(9)：75-78.

Huang Yunfeng. Design of restaurant food delivery system based on E-Puck robot autonomous patrol intelligent car[J]. Automation & Instrumentation, 2020(9): 75-78. (in Chinese with English abstract)

[4] 刘彩霞，顾帅，杨正涛. 校园送餐机器人控制系统的设计[J]. 制造业自动化，2021，43(1)：93-95.

Liu Caixia,Gu Shuai,Yang Zhengtao. Design of control system of campus meal delivery robot[J]. Manufacturing Automation, 2021, 43(1): 93-95. (in Chinese with English abstract)

[5] Jiang D L, Hu Y X, Yan S C, et al. Efficient 3D reconstruction for face recognition[J]. Pattern Recognition, 2005, 38(6): 787-798.

[6] 朱浩然，高琪，王洪平，等. 基于机器学习方法的三维粒子重构技术[J]. 实验流体力学，2021，35(3)：88-93.

Zhu Haoran, Gao Qi, Wang Hongping, et al. Particle reconstruction of volumetric particle image velocimetry with strategy of machine learning[J]. Journal of Experiments in Fluid Mechanics, 2021, 35(3): 88-93. (in Chinese with English abstract)

[7] 骆涌，周开邻，马琳，等. 多平行平面SEM图像的计算机辅助三维重构[J]. 电子显微学报，1996(6)：126.

Luo Yong, Zhou Kailin, Ma Lin, et al. Computer aided 3D reconstruction of multi parallel plane SEM images[J]. Journal of Chinese Electron Microscopy Society, 1996(6): 126. (in Chinese with English abstract)

[8] 宋小春，赵大兴，钟毓宁. 基于漏磁检测数据的缺陷三维重构技术[J]. 中国机械工程，2008，19(8)：905-908.

Song Xiaochun, Zhao Daxing, Zhong Yuning. 3D reconstruction technology of the MFL inspection data[J]. China Mechanical Engineering, 2008, 19(8): 905-908. (in Chinese with English abstract)

[9] Zhang Aiwu, Li Mingzhe, Hu Shaoxing, et al. 3D measurement technology based on computer vision[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2001, 17(1): 32-37.

张爱武，李明哲，胡少兴，等. 基于计算机视觉的三维测量技术[J]. 农业工程学报，2001，17(1)：32-37. (in English with Chinese abstract)

[10] Lehnert C, Mccool C, Sa I, et al. Performance improvements of a sweet pepper harvesting robot in protected cropping environments[J]. Journal of Field Robotics, 2020, 37(7): 1-27.

[11] 郭彩玲，宗泽，张雪，等. 基于三维点云数据的苹果树冠层几何参数获取[J]. 农业工程学报，2017，33(3)：175-181.

Guo Cailing, Zong Ze, Zhang Xue, et al. Apple tree canopy geometric parameters acquirement based on 3D point clouds[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(3): 175-181. (in Chinese with English abstract)

[12] 柴宏红，邵科，于超，等. 基于三维点云的甜菜根表型参数提取与根型判别[J]. 农业工程学报，2020，36(10)：181-188.

Cai Honghong, Shao Ke, Yu Chao, et al. Extraction of phenotypic parameters and discrimination of beet root types based on 3D point cloud[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(10): 181-188. (in Chinese with English abstract)

[13] 孔彦龙，高晓阳，李红玲，等. 基于机器视觉的马铃薯质量和形状分选方法[J]. 农业工程学报，2012，28(17)：143-148.

Kong Yanlong, Gao Xiaoyang, Li Hongling, et al. Potato grading method of mass and shapes based on machine vision[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(17): 143-148. (in Chinese with English abstract)

[14] 吴丹，叶军立，王康，等. 基于轮廓投影的盆栽水稻三维重建方法研究[J]. 中国农业科技导报，2020，22(9)：87-95.

Wu Dan, Ye Junli, Wang Kang, et al. Three-dimension reconstruction method based on silhouette for pot rice[J]. Journal of Agricultural Science and Technology, 2020, 22(9): 87-95. (in Chinese with English abstract)

[15] Hui F, Zhu J Y, Hu P C, et al. Image-based dynamic quantification and high-accuracy 3D evaluation of canopy structure of plant populations.[J]. Annals of Botany, 2018, 121(5): 1-10.

[16] Mortensen A K, Bender A, Whelan B, et al. Segmentation of lettuce in coloured 3D point clouds for fresh weight estimation[J]. Computers and Electronics in Agriculture, 2018, 154: 373-381.

[17] Li X Z, Mao K Z, Lin F F, et al. Particle swarm optimization with state-based adaptive velocity limit strategy[J]. Neurocomputing, 2021, 447: 1-16.

[18] 王晓东，胡松钰. 激光结构光测量连续调节智能光源控制器设计[J]. 红外与激光工程，2021，50(3)：165-173.

Wang Xiaodong, Hu Songyu. Research on echo filtering algorithm of multi pulse laser range extended target in dynamic clutter background of airborne platform[J]. Infrared and Laser Engineering, 2021, 50(3): 165-173. (in Chinese with English abstract)

[19] 张建宇，高天宇，于潇雁，等. 基于自适应时延估计的空间机械臂连续非奇异终端滑模控制[J]. 机械工程学报，2021，57(11)：177-183.

Zhang Jianyu, Gao Tianyu, Yu Xiaoyan, et al. Continuous non-singular terminal sliding mode control of space robot based on adaptive time delay estimation[J]. Journal of Mechanical Engineering, 2021, 57(11): 177-183. (in Chinese with English abstract)

[20] Shu L, Schlüter A D, Ecker C, et al. Extremely long dendronized polymers: Synthesis, quantification of structure perfection, individualization, and SFM manipulation[J]. Angewandte Chemie, 2001, 113: 4802-4805.

[21] Kumar P, Henikoff S, Ng P C. Predicting the effects of coding non-synonymous variants on protein function using the SIFT algorithm.[J]. Nature Protocols, 2009, 4(8): 1073-1081.

[22] Hu K, Jiang M, Zhang H, et al. Design of fault diagnosis algorithm for electric fan based on LSSVM and Kd-Tree[J]. Applied Intelligence, 2021, 51(6): 1-15.

[23] Schnabel R, Wahl R, Klein R. Efficient RANSAC for point-cloud shape detection[J]. Computer Graphics Forum, 2010, 26(2): 214-226.

[24] 刘宇，熊有伦. 基于法矢的点云拼合方法[J]. 机械工程学报，2007(8)：7-11.

Liu Yu, Xiong Youlun. Registration method for point clouds based on normal vectors[J]. Journal of Mechanical Engineering, 2007(8): 7-11. (in Chinese with English abstract)

[25] Tordoff B J, Murray D W. Guided-MLESAC: Faster image transform estimation by using matching priors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1523-1535.

[26] 张恒康，何玉明，张耿耿，等. 一种单相机测量三维运动轨迹的方法[J]. 固体力学学报，2010，31(S1)：171-176.

Zhang Hengkang, He Yuming, Zhang Genggeng, et al. A new method of binoculars stereo vision with single camera[J]. Chinese Journal of Solid Mechanics, 2010, 31(S1): 171-176. (in Chinese with English abstract)

[27] Granshaw S I. Bundle adjustment methods in engineering photogrammetry[J]. The Photogrammetric Record, 2006, 10(56):181-207.

[28] Gong S N, Kumar R, Kumutha D. Design of lighting intelligent control system based on OpenCV image processing technology[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2021, 29(Suppl 1): 1-21.

[29] 屈立成，吕娇，赵明，等. 基于三维时空地图和运动分解的多机器人路径规划算法[J]. 计算机应用，2020，40(12)：3499-3507.

Qu Licheng, Lü Jiao, Zhao Ming, et al. Multi-robot path planning algorithm based on 3D spatiotemporal maps and motion decomposition[J]. Journal of Computer Applications, 2020, 40(12): 3499-3507. (in Chinese with English abstract)

[30] Shewchuk J R. Delaunay refinement algorithms for triangular mesh generation[J]. Computational Geometry Theory & Applications, 2014, 47(1/2/3): 741-778.

Algorithm for the uniform petal carving of Hami melon based on three-dimensional reconstruction

Zhao Mingyan1, Lin Min1, Xu Peng2※, Wang Yongjin1, Song Tianyue1, Liang Mingxuan1,Hu Jianhong1

(1.,,310018,; 2.,,310018,)

Higher carving speed and uniform petal size of Hami melon are critical for the robot carving Hami melon. It is very necessary to plan the cutting path of the execution terminal (carving knife) in real-time, according to the three-dimensional coordinates of different processing objects. In this study, a uniform petal carving of Hami melon was proposed using point cloud splicing. The image features were extracted and reconstructed sparsely. The feature parameters of melon were firstly obtained by point cloud coordinates. Secondly, CMVS/PMVS algorithm was selected for dense reconstruction using the sparse points. Finally, the octree and Poisson surface reconstruction were used to obtain the accurate 3D spatial coordinates of melon. Different shapes of Hami melon was led to different reconstructions. Each piece of flesh presented the same volume after carving. The specific procedure was as follows. Firstly, the cutting height and depth of melon were determined to extract the point cloud. An arc function was then fitted to determine the center of the circle, according to the point cloud of the outermost circle of Hami melon. The number of carving petals was divided 360° to determine the pre carving start point, end point, and path. Specifically, the initial triangle was formed to search for the two closest points from any point in the numerous point clouds as the benchmark, and then to expand the triangle outward with the three sides of the triangle as the baseline, where the equal volume of each petal was taken as the objective function, while the equal cutting depth and cutting angle of each petal as the limiting conditions. Until all the point clouds were included in the three-dimensional triangle network, the area of the projected triangle was calculated by the Helen formula, where the average value for thecoordinates of three projected points was taken as the height, and then to calculate the volume of the triangular pyramid. After depth-first and particle swarm optimization, the optimal solution was found in the coordinates of Hami melon point cloud through continuous recursive iteration. Finally, better cloud coordinates were stored as new datasets and then marked on the outside of Hami melon. As such, the manipulator was controlled to evenly carve the Hami melon. Specifically, the cutter first adjusted to the appropriate posture angle as posture point 2, then moved along the cutter ridge to a certain depth to posture point 1, and retreated to posture point 3, and finally, the cutter moved along the outer surface of Hami melon to the next adjacent posture point 2. These steps were repeated to complete the overall carving of the Hami melon. The regular and irregular models were also selected to verify the accuracy. The calculated volumes of cube, pyramid, and irregular body were compared with the real. 48 Hami melons (16 groups, 3 in each group) were divided, where the number of carved petals was 15-30, and the carving depth was 1.5, 2.0, and 2.5 cm. It was found that the precision of the group was the lowest with the number of cut petalsequal to 28. The maximum and minimum petal volumes were measured as 3.40 and 3.25 cm3, respectively, where the maximum volume difference was 0.15 cm3, and the error was less than 5%. Consequently, the melon petal carving using point cloud splicing presented a higher precision than before. The findings can provide strong technical support for robot carving Hami melon.

image processing; Particle Swarm Optimization(PSO); 3D reconstruction; uniform petal carving; point cloud splicing; triangular meshing

赵明岩，林敏，徐鹏，等. 基于三维重构的哈蜜瓜均瓣雕花算法[J]. 农业工程学报，2021，37(19)：276-283.doi：10.11975/j.issn.1002-6819.2021.19.032 http://www.tcsae.org

Zhao Mingyan, LinMin, Xu Peng, et al. Algorithm for the uniform petal carving of Hami melon based on three-dimensional reconstruction[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(19): 276-283. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.19.032 http://www.tcsae.org

2021-05-22

2021-07-22

国家自然科学基金（51876196）和国家自然科学基金青年基金（51705494、51605462）

赵明岩，副教授，研究方向为智能农业装备及农业机器人。Email：zhaomingyan@cjlu.edu.cn

徐鹏, 博士，教授，研究方向为计算机仿真和工业传输过程。Email：xupeng@cjlu.edu.cn

10.11975/j.issn.1002-6819.2021.19.032

TP391.41

A

1002-6819(2021)-19-0276-08