均匀圆阵相关干涉仪相位模糊问题研究

姚家苗，郑林华，杨 鹏

(国防科技大学，湖南 长沙 410073)

0 引 言

相位干涉仪测向是通过测量入射信号在间距一定的两天线间的相位差来确定信号来波方向的测向方法，由于具有覆盖频段宽、测角速度快、精度高、技术成熟等优点，得到了广泛的应用[1]。相位干涉仪孔径越大，测角精度越高；但是当基线大于半波长时，会出现相位模糊问题，基线越长，模糊数越大，解模糊算法越复杂。为了解决这一矛盾问题，国内外学者提出了很多解相位干涉仪模糊的理论方法，如长短基线法、参差基线法、虚拟基线法、立体基线法、基于扩展基线法、基于平行基线法、基于相关比幅法、基于时差解模糊算法等[2-3]。这些方法虽然能够在一定程度上解决这些矛盾，但是解模糊算法大都比较复杂，而且不能确保解模糊正确性，特别是在信噪比不是很高时很可能会因为解模糊错误而导致最终无法正确测向，此外，采用解模糊技术的测向方法还可能会受到天线阵形摆放单一的限制[4]。这些都制约了相位干涉仪的发展与应用，采用相关干涉仪可以很好地解决上述问题。

相关干涉仪是在相位干涉仪的基础上发展而来，由于具有更高的测角精度，更适合用数字处理方式实现，而且可以消除和减弱天线互耦、通道不一致等因素的影响，所以相关干涉仪测向体制成为当前最流行的测向体制[5]。随着空间通信信号的高频化，空间测角信号波长变得越来越短，如某机群使用频率为21 GHz的信号进行测向，其波长只有约14 mm。如果半径波长比取值较小，天线阵半径就会很小，阵元间互耦现象会比较严重，这对于工程实现是十分不利的。而且对于均匀圆阵相关干涉仪，通常半径越大，测角精度越高，然而天线半径波长比过大，则可能出现相位模糊问题。当前，国内外对于超高频信号条件下均匀圆阵相关干涉仪测角研究较少，使用的信号频率主要集中在10 GHz以内，对半径波长比以及测角精度要求相对较低，因此对半径波长比与测角精度和相位模糊的关系缺乏专门研究。对于高频信号测角，其天线阵半径波长比通常取值较大，此时会不会出现相位模糊，是高频信号相关干涉仪测角工程实现必须解决的问题。

1 均匀圆阵相关干涉仪测角基本原理

相关干涉仪测角算法依据所测信号的相位差与样本库的相关性进行测角，通过引入相位差来避免出现相位模糊，具有较高的精度[6]。相关即“比较”的意思，就是将鉴相器测得的各阵元间的相位差组成的相位差矢量与事先建立好的样本库中所存储的相位差矢量做相关匹配运算，在样本库中找出与这个实际测量的相位差矢量最接近的一组样本相位差矢量，再根据样本库信息，可以得到与之相对应的入射角度值，实现对入射信号的测向[7]。其天线阵面如图1所示。

图1 M元均匀圆阵相关干涉仪阵面示意图

图1中，圆阵半径为R，圆心处阵元1为参考点，以圆心与阵元2的连线作为Y轴，M个阵元均匀分布在圆周上。假设入射信号以方位角θ和俯仰角β入射到天线阵面，则第m个阵元相对于参考点的时延为：

(1)

相应的相移为：

(2)

以圆心处的天线1作为参考天线，其他天线与天线1组成M组天线对，求解M组天线的相位差。根据上面的相移公式，方位角和俯仰角均以一定的间隔建立相位差样本库，每个样本矢量中包含M个相位差值。当信号从某一方向入射到阵列时，通过鉴相器可以测得M组天线相对于参考点的相位差值，将这M个相位差值与样本库中的相位差矢量进行相关运算，通过搜索相关峰即可求出入射信号方位信息。

2 均匀圆阵相关干涉仪无相位模糊条件分析

当前大部分文献都默认相关干涉仪无需解相位模糊，但对于相关干涉仪是否会出现相位模糊、为何不需要解模糊，还没有文献进行专门研究。作为一种特殊的相位干涉仪，相关干涉仪在超出一定的条件后也会出现相位模糊问题，目前相关干涉仪所使用的信号频率不高，对测角精度要求也不是很高，所采用的半径波长比相对较小，符合相关干涉仪无相位模糊的条件，因此不需要解相位模糊。随着信号频率的提高，当波长达到毫米级甚至更短的时候，如果还采用半径波长比较小的天线，这在工程上将很难实现，而且对于相关干涉仪，基线越长，测角精度越高，那么为了提高测角精度，均匀圆阵相关干涉仪半径是否越大越好，半径波长比应满足什么条件才不会出现相位模糊，实际应用中半径波长比最佳取值范围是什么，这些问题对于均匀圆阵相关干涉仪的工程应用尤其是高频信号测角的实现具有十分重要的意义。

引起相位模糊的根本原因在于当基线长大于半波长时，两天线间的相位差可能会超过2π，而鉴相器只能输出(-π，π]的测量值，导致实际测量的相位差存在多值情况，从而产生相位模糊问题[8]。对于M元均匀圆阵相关干涉仪，由于是使用了M个相位差构建的相位差矢量进行相关运算，所以只有当M个相位差均存在相位模糊时，测向才会出现相位模糊。不考虑噪声干扰的影响，假设M元均匀圆阵相关干涉仪存在相位模糊，即存在2组不同时相等的方位角θ1、θ2，俯仰角β1、β2，根据相移公式(2)所得到的M组相位差均相差2π的整数倍，即：

(3)

式中：km-1∈Z，为模糊周期数。

对式(3)进行变换，可得到：

(4)

对式(4)进一步化简可得到：

(5)

令cosθ1sinβ1-cosθ2sinβ2=w，sinθ1sinβ1-sinθ2sinβ2=v，式中θ1=θ2和β1=β2不同时成立，则式(5)可以等价为：

(6)

根据上式，可得到M个等式方程构建的方程组：

(7)

求出上述方程组无解的条件，即可得出窄带信号条件下M元均匀圆阵相关干涉仪测角理论上无相位模糊的条件。根据线性方程组求解的条件可知，当方程组系数矩阵的秩小于方程组增广矩阵的秩时，方程组无解。因为式(7)系数矩阵的秩为2，因此式(7)无解的条件为：

rankA=

下面以5元均匀圆阵相关干涉仪为例进行求解，对于5元均匀圆阵相关干涉仪，上述方程组可写为：

(8)

根据线性方程组求解的条件可知，式(8)无解等价于：

若要使上述矩阵的秩小于3，则有：

(9)

式中:k1，k2，k3，k4，k5∈Z，由式(9)可得：

(10)

式(10)中，由于k1，k2，k3，k4，k5∈Z，所以k3+k4∈Z,k2+k5∈Z。式(10)要成立，①当k1=0时，有k1=k2=k3=k4=k5=0或|k2|≥500，|k5|≥500，|k3|≥809，|k4|≥809；②当k10时，则有|k1|≥500。综上所述，若要式(10)成立，则有k1=k2=k3=k4=k5=0或|k2|≥500或|k1|≥500，由于km-1为实测相位模糊周期数，且|km-1|=[L/λ]，因此可得5元均匀圆阵相关干涉仪单频信号条件下理论上无相位模糊的最大基线波长比为：R/λ=500。对于M元均匀圆阵相关干涉仪求解方法与5元相类似。由于实际应用中，半径波长比不可能取到如此之大，因此圆阵相关干涉仪一般不会出现相位模糊问题。

3 仿真实验与结果分析

本文主要以圆心为参考点的5元均匀圆阵相关干涉仪为例进行仿真和分析，首先对信噪比为5 dB，信号频率为21 GHz(波长约为14 mm)，标准阵步长为0.2 ，仿真次数为1 000次，方位角为-180°～180°，俯仰角为-65°～65°条件下不同半径的天线测量误差值进行仿真，结果如图2～图7所示。

图2 半径为14 mm的仿真结果

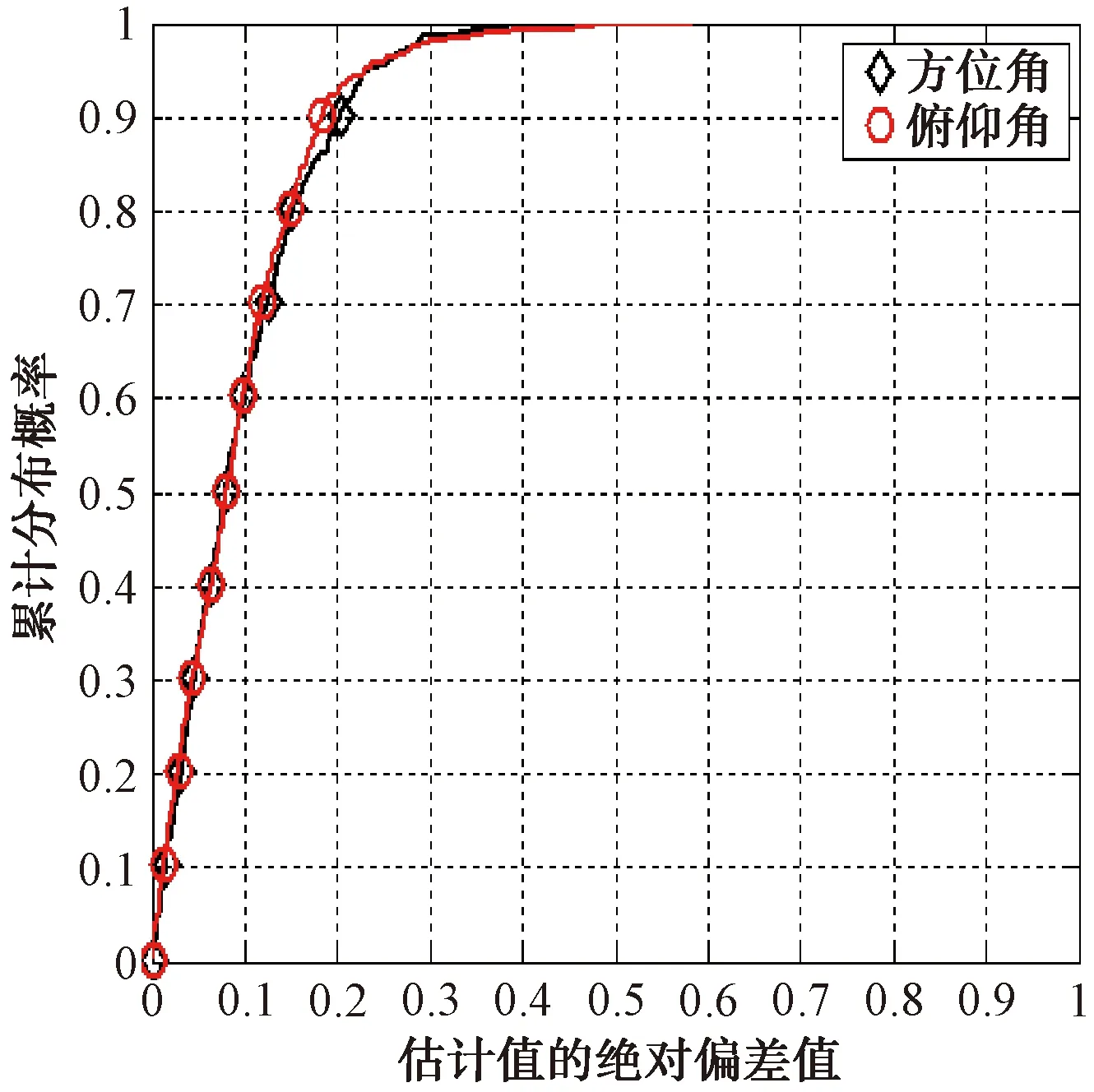
图3 半径为40 mm的仿真结果

图4 半径为140 mm的仿真结果

图7 半径为700 mm的仿真结果

图2～图7的横坐标为测量的误差值，纵坐标为误差累积分布概率值。从仿真结果可以看出，在信噪比、信号频率、标准阵步长一定的条件下，当半径在一定范围内时，随着半径的增大，测角精度不断提高，而一旦超出阈值范围，测角精度会急剧下降。下面通过对不同半径波长比条件下相关峰的情况进行仿真，分析出现这种现象的原因，如图8～图11所示。

图8 半径波长比为1时相关值示意图

图10 半径波长比为10时相关值示意图

图11 半径波长比为50时相关值示意图

从仿真结果可以得出，出现这种情况的原因主要是：在信噪比一定的条件下，半径波长比较小时相关峰比较平坦，进行相关匹配时，相邻的角度不好区分，因此精度较低，随着半径波长比的增加，相关峰峰值变得尖锐且密集，比较容易分辨，因此测角精度会提高。但当半径波长比达到一定的值后，旁瓣会变得十分密集，相关峰宽度会变得十分窄，此时测角结果受噪声影响很大，轻微的噪声都会造成峰值的变化，而且如果不缩小搜索步进，很可能会因为跳过相关峰而出现测角错误[9]。为了验证上述分析，对半径为280 mm、420 mm、700 mm条件下提高信噪比、减小标准阵步长进行仿真，仿真结果如图12～图14。

图12 半径280 mm，信噪比25 dB,步长0.2的仿真结果

图13 半径420 mm,信噪比25 dB，步长0.05的仿真结果

图14 半径700 mm，信噪比50 dB，步长0.01的仿真结果

对比图5、6、7和图12、13、14，可以看出，在半径波长比较大的情况下，提高信噪比、减小标准阵步长能够显著改善测角精度。当信噪比取足够大、标准阵步长足够小时，则可验证半径波长比小于500时能够正确测向而不会出现相位模糊，证明上述分析的正确性。实际应用中，由于信噪比通常取值有限，而标准阵步长过小会大大增加系统存储量和运算量，因此半径波长比不能过大。对于相关干涉仪基线越长测角精度越高，但基线波长比越高，对信噪比要求越高，超过一定的门限后如果不减小步长，测角精度也会急剧下降。下面在其他条件不变的情况下，对不同半径波长比的天线在信噪比为-5 dB、步长为0.2的条件下进行仿真，仿真结果如图15～图18所示。

图15 半径为14 mm的仿真结果

图17 半径为140 mm的仿真结果

图18 半径为280 mm的仿真结果

从图15可以看出，在信噪比较低的情况下，半径波长比为1时，测角误差在0.5°范围以内的累积概率只有50%，测角精度相对较低；从图16、17可以看出，在信噪比比较低的情况下，半径波长比在2～10之间时，测角精度相对较高；从图18可以看出，半径波长比过大时，测角精度受信噪比影响急剧降低。通过对不同条件下5元均匀圆阵相关干涉仪进行大量的仿真可以得出：半径波长比在2～10之间时，测角精度相对较高而且受信噪比影响较小，因此对于以圆心为参考点的5元均匀圆阵相关干涉仪，半径波长比的最佳取值应为2～10之间。

图16 半径为40 mm的仿真结果

4 结束语

对于均匀圆阵相关干涉仪，当基线波长比超过一定的门限，就会出现相位模糊问题。本文提出了求解M元均匀圆阵相关干涉仪无相位模糊条件的方法，并以5元均匀圆阵相关干涉仪为例，求出了无相位模糊的条件，通过仿真进行了验证，分析了测角精度与半径波长比、信噪比、标准阵步长的关系以及均匀圆阵相关干涉仪测角精度随着半径波长比呈现先增大后急剧下降的原因，并通过仿真分析得出了5元均匀圆阵相关干涉仪在实际应用中半径波长比的最佳取值范围，对于高频信号高精度测角的实现具有重要的参考意义。