郑州西流湖大桥车辆激励作用对人行桥舒适性的影响分析
2021-12-27刘亚尊王博妮
任 辉 刘亚尊 王博妮
(中铁工程设计咨询集团有限公司郑州设计院,郑州 450001)
郑州西流湖大桥跨越区域位于某公园园区,由于桥下净空受限,为实现公园人行道路与市政道路的衔接,考虑采用人行与车行分离的方案。在满足市政车行的前提下,利用主桥两侧空间设置专用人行桥满足人行需求的同时兼顾景观功能。人行桥与车行主桥采用横向联系成为一体,两桥之间具有耦合效应,结构的动力特性由车行桥与人行桥共同决定,其中,人行桥的动力特性(尤其是自振频率)对桥梁舒适性有重要影响。
目前,国内对于此类组合式桥梁的应用和研究较少,马如进等以吴淞江大桥为研究对象,根据能量原理研究车行桥与人行桥的刚度比及质量比对结构自振频率的影响规律,评价车致振动效应对人行桥的影响[1]。考虑西流湖大桥情况更加复杂,人行桥梁型为变高变宽空间截面,故需对该桥结构形式进行针对性分析。
1 工程概况
西流湖大桥车行主桥采用(31+48+72+48+31) m变截面混凝土连续箱梁。主梁采用鱼腹式截面,支点梁高4.5 m,跨中梁高3 m,箱梁顶板宽22.0 m。左、右侧人行桥采用(48+72+48) m连续刚构体系,上部结构采用鱼腹式钢箱梁结构,梁高2.0~3.0 m,宽3.0~6.0 m。车行桥与人行桥之间通过矩形钢横梁连接,矩形钢横梁预埋于车行桥内并与人行桥焊接。钢横梁设置范围为支点两侧各23 m。为提高桥梁景观效果,横向联系为反对称设置(见图1、图2)。

图1 西流湖大桥
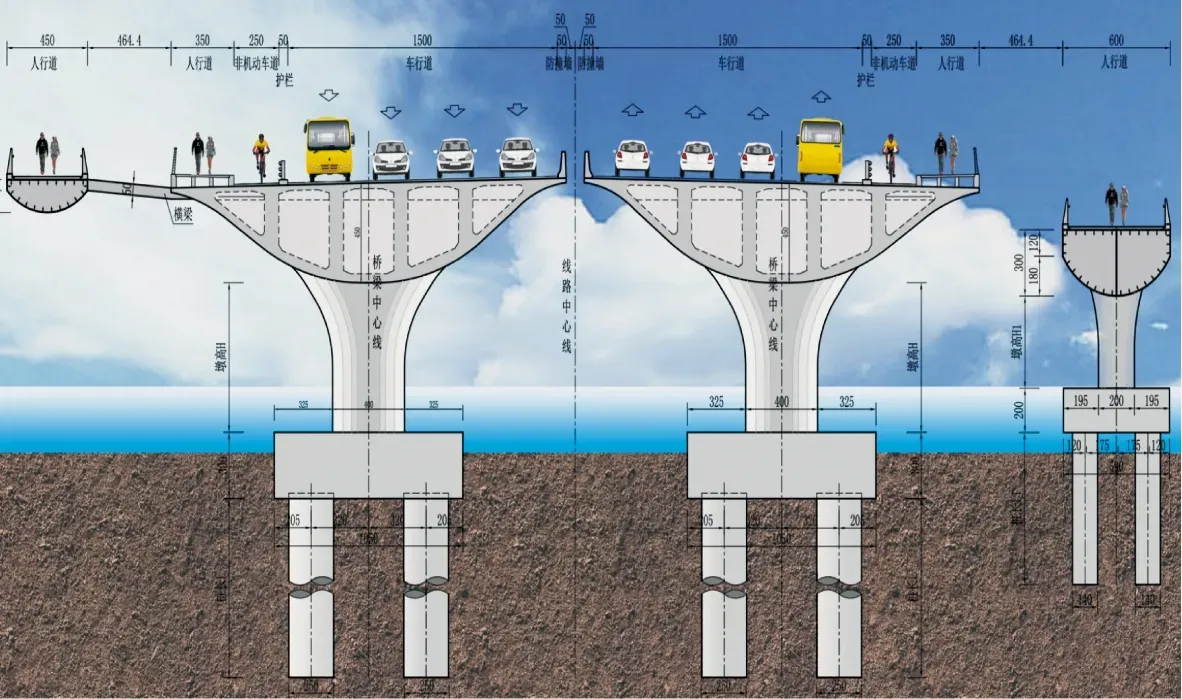
图2 西流湖大桥横断面示意(单位:cm)
2 结构受力性能分析
采用Midas/Civil2019有限元软件,建立空间结构模型(见图3),以理论纵曲线为基准进行结构离散。车行桥及人行桥均采用梁式单元,横向矩形钢横梁通过“刚性连接+横向单元”模拟,以连接人行桥与车行桥,其刚度根据矩形钢横梁的长度和截面特性推算,梁与主墩通过刚性连接实现固结。

图3 全桥有限元模型
将人行桥-车行桥组合式桥梁作为整体,按施工流程逐阶段计算结构各截面内力、应力和位移。计算内容包括恒载、车辆活载、混凝土收缩徐变、预应力、温度变化、风载、汽车制动力、支座沉降等。
车行桥及人行桥在施工、运营阶段下的结构受力情况见表1[2]。
由表1可知,在施工阶段混凝土梁全截面处于受压状态,最大压应力为9.3 MPa;钢箱梁最大压应力为36.4 MPa,最大拉应力为2.6 MPa,均满足规范要求。
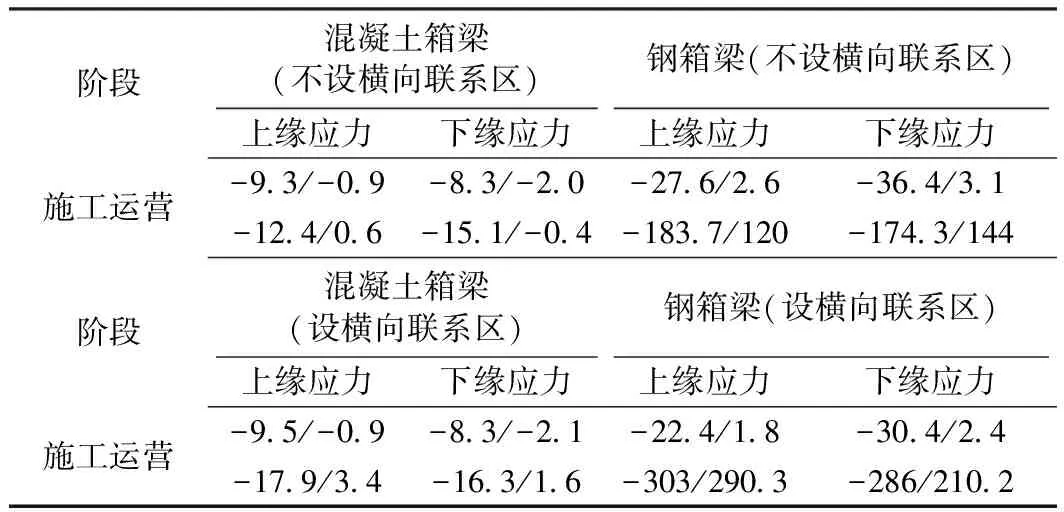
表1 主要计算结果 MPa
运营阶段混凝土梁及钢箱梁上下缘应力在横向联系区范围内出现明显突变,混凝土连续梁最大压应力为17.9 MPa,最大拉应力为3.4 MPa;钢箱梁第一体系与第二体系叠加后,最大压应力为303 MPa,最大拉应力为290.3 MPa;均超出规范要求。
在不设横向联系区,混凝土连续梁最大压应力为15.1 MPa,最大拉应力为0.6 MPa;钢箱梁最大压应力为183.7 MPa,最大拉应力为144 MPa;没有出现明显的突变。
根据计算结果,在恒载作用下,设横向联系区与不设横向联系区混凝土连续梁及钢箱梁应力相差不大;运营阶段,设横向联系区与不设横向联系区刚度相差过大,在车辆作用、温度效应等影响下,横向联系区会出现耦合振动,导致应力分布出现突变。
参考相关文献[3-4],综合考虑车辆的变速运动、横向连接刚度等影响系统振动等因素[5],可推导出横向联系的刚度和边界条件。
3 车桥耦合振动分析
3.1 车桥耦合振动分析
以车轮和桥面作为接触边界条件,分别建立车、桥系统的运动方程[6],其运动方程可分别表示为
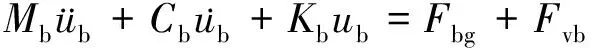
(1)
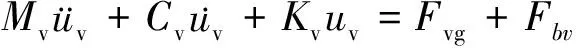
(2)
式中,Fbg和Fvg分别为作用在桥梁和车辆的与桥梁车辆运动无关的荷载(如自重);Fvg和Fbv分别表示车-桥系统间的相互作用力。
车桥系统运动方程的求解采用ANSYS有限元软件实现。桥梁简化模型见图4。
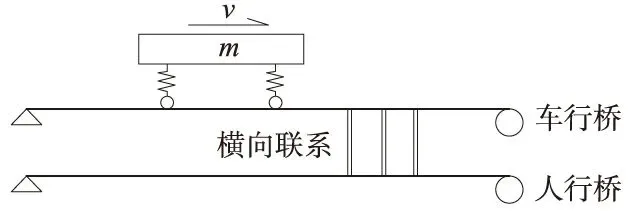
图4 桥梁简化模型
建立车辆模型,车辆简化为弹簧-阻尼-质量系统,将车辆的上桥时间、行驶初速度、加速度、行驶方向、路面粗糙度等参数输入模型[7]。进入ANSYS 瞬态动力分析,确定时间步长,赋予初始条件,得出车轮接触桥梁节点的位移、速度及加速度。并根据位移协调条件求得t时刻车桥相互作用力,循环迭代可得出任意截面的时程曲线。
3.2 结果分析
不同车速下车行桥跨中挠度见图5,不同车速下人行桥跨中挠度见图6。
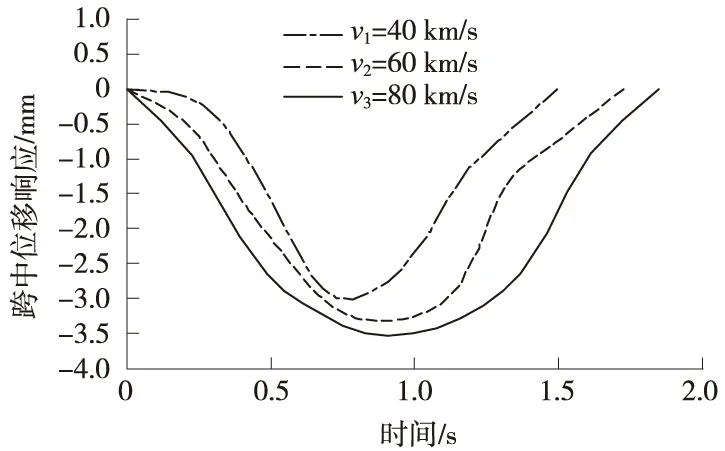
图5 不同车速下车行桥跨中挠度
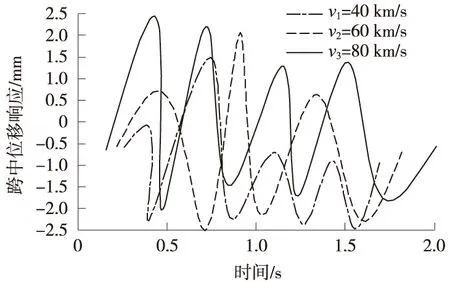
图6 不同车速下人行桥跨中挠度
V=60 km/s时不同横向联系刚度人行桥跨中挠度见图7,车辆速度不变的情况下,横向联系刚度k=100时,跨中挠度Zmax=2.5 cm;横向联系刚度k=5时,跨中挠度Zmax=0.8 cm,说明横向联系刚度对钢结构桥影响显著。
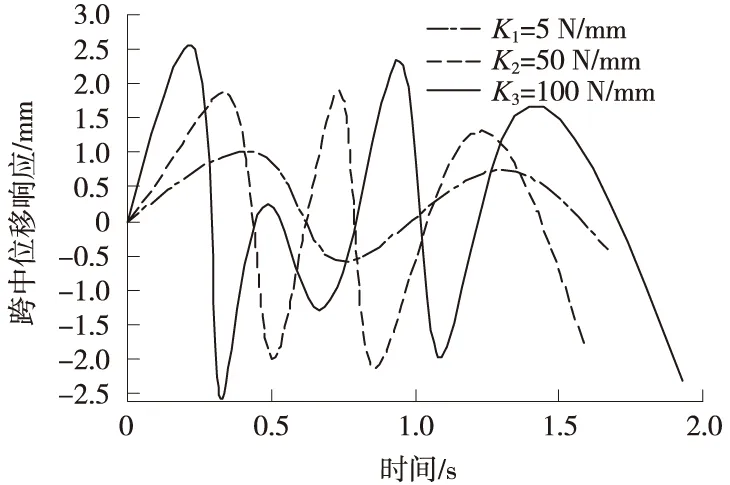
图7 V=60 km/s时不同横向联系刚度人行桥跨中挠度
横向联系改变了钢结构桥的刚度分布,减小横向联系刚度可显著减小钢结构桥的耦合作用。通过调整横向联系的刚度分布矩阵,可有效改善钢结构桥的畸变效应。
钢结构桥一般跨径较大,加之竖曲线和平曲线的影响,质量分布不规律,在风载、人群荷载激励下自身也会产生振动[9]。为保证结构舒适性和安全性,在刚度调节的基础上,采用加装TMD调制阻尼器方案解决振动问题[10-13]。
4 人行桥阻尼减震设计
4.1 主梁模态分析
在人行桥的动力分析模型中,暂不考虑人群等荷载对频率的影响,质量分布仅为结构恒载。
通过模态分析,分析研究人行桥的自振特性,进行阻尼减振设计[14],桥梁各阶振型见图8~图11。
由图8~图11可以看出,一阶竖弯振型为主梁的对称弯曲振型,振型最大点位于主跨跨中。

图8 一阶振型(主梁对称弯曲为主,1.811 Hz)

图9 二阶振型(主梁纵向位移为主,2.438 Hz)

图10 三阶竖向弯曲振型(2.621 Hz)

图11 四阶竖向弯曲振型(3.245 Hz)
二阶振型以纵向位移为主,在竖向亦有振动位移,竖向位移最大点在主跨距离第一个桥墩41 m处。
三阶振型以第一跨主梁的竖向弯曲振型为主,振型的最大点位于第一跨跨中附近。
四阶竖弯振型的最大点位于第一跨跨中位置及距离第一个桥墩27 m处。
1)减轻地表水。根据对滑坡地质灾害的了解,结合其灾害的影响因素,提出减轻地表水的危害治理措施,是十分重要的。根据对以往滑坡地质灾害的分析,70%的滑坡灾害发生的主要原因是地表水过多。在对地表水治理时,要采用合理的方式对地表水进行拦截和导引。在对地表水进行拦截和导引时,可以根据滑坡周围山体情况和水流走向,对地表水进行拦截和改流,避免地表水流入滑坡区域内,引发二次滑坡。
上述计算中,只考虑了桥梁的恒载作用,未考虑人群等附加荷载,这在一定程度上起到降低桥梁频率的作用[15]。通过计算可以看出,对可能发生振动的振型主要为上述分析出的主梁前四阶振型,对应的模态参数见表2。
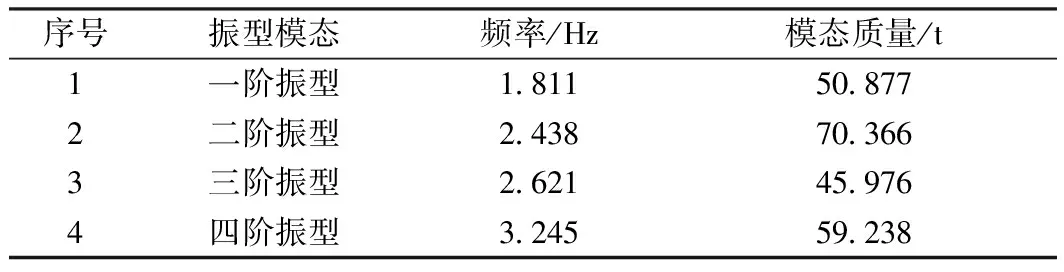
表2 主梁振型模态参数
通过分析,荷载对桥梁的激励是施加在主梁上,上述几种振动模态频率较小,在荷载激励下可能产生较大的振动幅值,故需对其进行控制。
4.2 阻尼器参数设计
参考公路桥梁抗风设计规范[16],不同结构形式的桥梁阻尼比数值为:钢箱梁 0.003,钢混结合梁桥0.01,混凝土桥0.02,人行桥主梁0.003。
经研究,行人的敏感步频为1.5~3.0 Hz。各阶振型频率均处于行人敏感步频范围内,振动激励的概率较大,按照质量比μ=2%进行TMD设计。各阶阻尼器的布置及附加质量统计见表3。
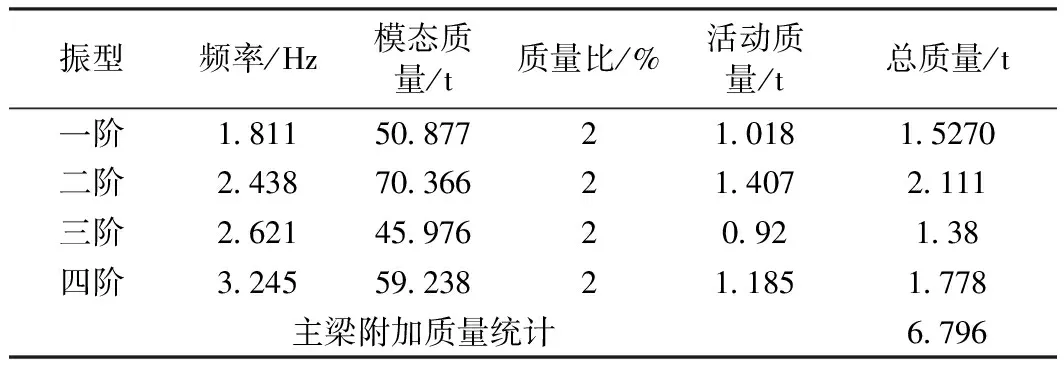
表3 阻尼器布置及附加质量统计
4.3 各阶振型阻尼器安装位置
一阶竖向振型的最大值在跨中,故TMD-1阻尼器宜安装在主跨跨中位置,根据同样的原则,阻尼器均安装在振型振幅最大值附近(见图12),TMD-2阻尼器安装在主跨距离第一个桥墩中心41 m处。对应三阶振型的TMD-3阻尼器安装在第一跨距桥墩中心24 m处。四阶振型的TMD-4阻尼器安装在第一跨跨中以及主跨距离第一个桥墩中心27 m处。
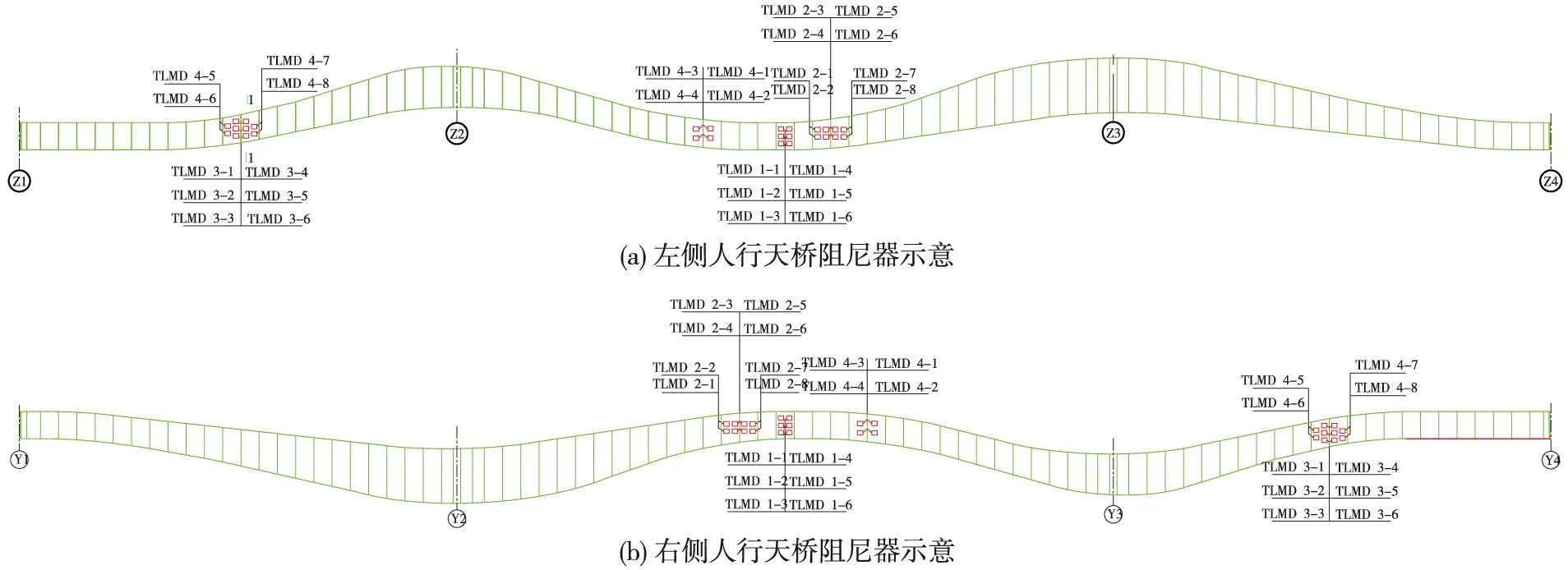
图12 阻尼器安装位置示意
4.4 各阶阻尼器参数优化
对上述各阶振型对应的阻尼器进行设计优化后,阻尼器具体设计参数见表4。
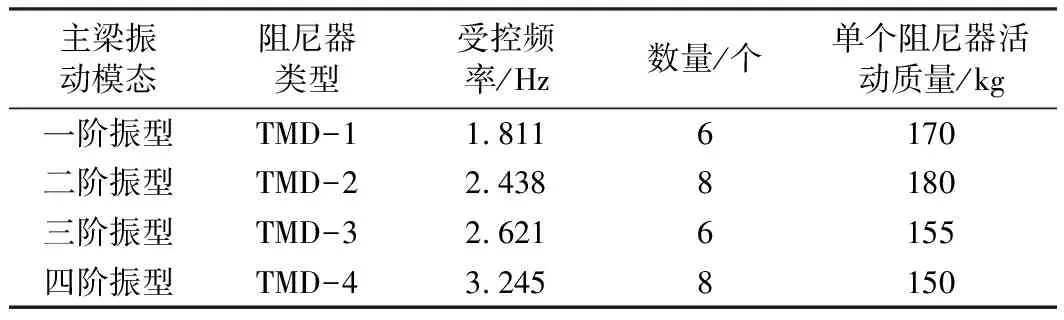
表4 主梁TMD参数
采用小型、频率分布式TMD方案,以方便TMD阻尼器在成桥后的安装,同时可保证荷载引起的频率下降后的振动控制效果。安装TMD阻尼器前后人行桥受力情况见表5,减振效果见图13。

表5 TMD阻尼器后人行桥结果对比 MPa
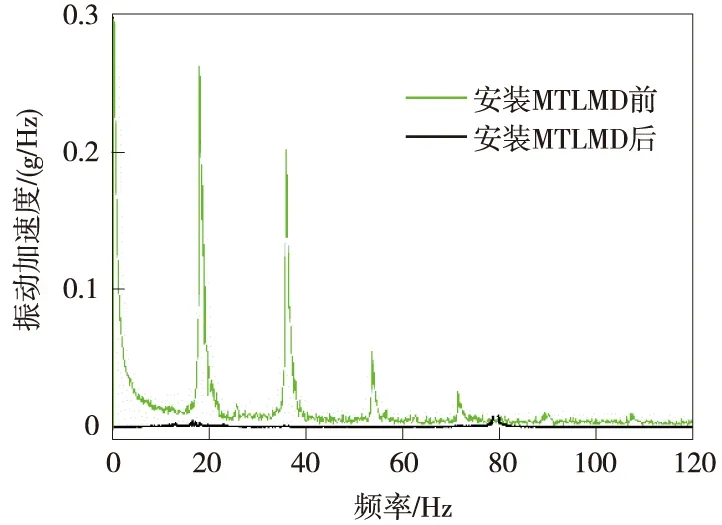
图13 安装TMD阻尼器前后减振效果对比
由图13可知,安装TMD的结构振动衰减速度较快,可有效抑制结构在人行荷载和行车激励下的振动,减振效率达91.3%。
5 结语
跨西流湖大桥是郑州市金水路西延重难点控制性工程,采用钢箱梁-预应力混凝土连续梁的组合体系桥型结构。通过对组合体系进行静力分析、车-桥耦合振动分析,调整横梁刚度分布,使结构受力满足了要求;同时,采用TMD设计限制人行桥的耦合振动,保证了桥梁后期行人的舒适性。
