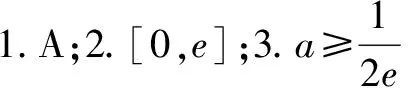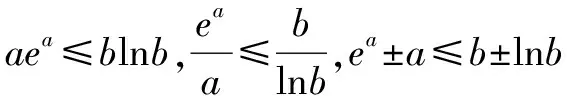指对跨阶“同构法”求解不等式恒成立问题

杨瑞强

(湖北省黄石市第一中学 435000)

把一个等式或不等式通过变形，使左右两边结构形式完全相同，可构造函数，利用函数的单调性进行处理，找这个函数模型的方法就是同构法.例如若F(x)≥0能等价变形为能等价变形为能等价变形为f[g(x)]≥f[h(x)]，然后利用f(x)的单调性(如递增)，再转化为g(x)≥h(x).在遇到“指数函数和对数函数”同时出现的试题时，我们可考虑采用“同构”的方法变形转化，构造函数，从而达到化难为易，删繁就简的功效.

一、积型aea≤blnb同构

三种同构途径：①同左aea≤(lnb)elnb，构造函数f(x)=xex；②同右ealnea≤blnb，构造函数f(x)=xlnx；③取对数a+lna≤lnb+ln(lnb)，构造函数f(x)=x+lnx.

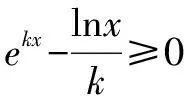
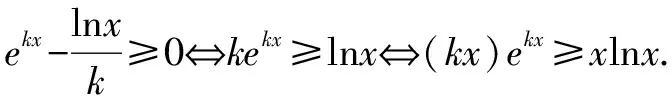
解法1(构造同左aea≤(lnb)elnb形式)(kx)ekx≥xlnx⟺(kx)ekx≥(lnx)elnx.

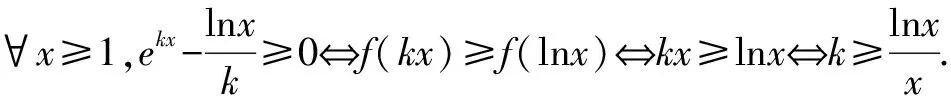
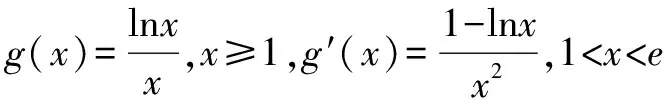
解法2(构造同右ealnea≤blnb形式)(kx)ekx≥xlnx⟺ekxlnekx≥xlnx.

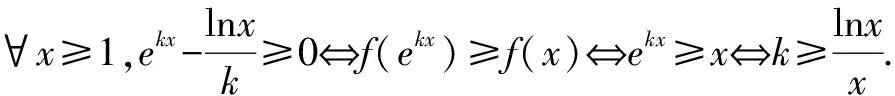
解法3(取对数a+lna≤lnb+ln(lnb)形式)(kx)ekx≥xlnx⟺kx+ln(kx)≥lnx+ln(lnx).

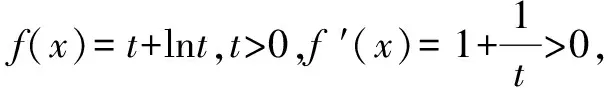
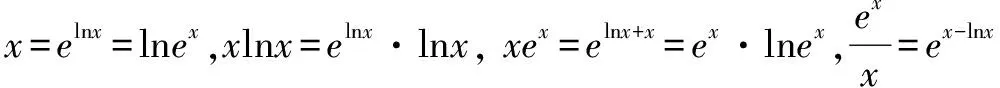
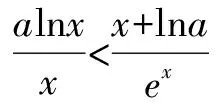
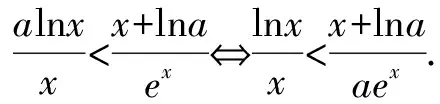
解析由已知可得a>0.

当a≥1时，不等式左边小于0，右边大于0，不等式显然成立.

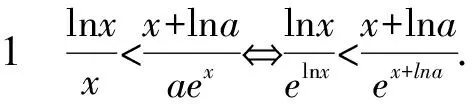
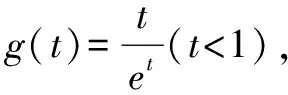
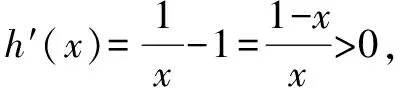
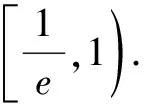
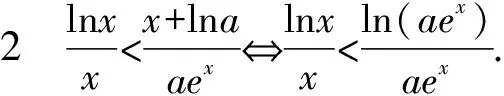
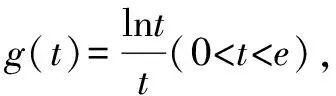
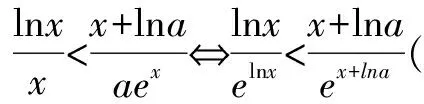
三、和差型ea±a≤b±lnb同构

两种同构途径：①同左ea±a≤elnb±lnb，构造函数f(x)=ex±x；②同右ea±lnea≤b±lnb，构造函数f(x)=x±lnx.

例3已知函数f(x)=aex-1-lnx+lna，若f(x)≥1，求a的取值范围.

解析将f(x)≥1按照左右结构相同、变量移至一边的原则进行变形：

由f(x)=aex-1-lnx+lna≥1，移项得aex-1+lna≥lnx+1，即elna+x-1+lna≥lnx+1，两边同时加(x-1)得elna+x-1+x+lna-1≥lnx+x，即elna+x-1+(x+lna-1)≥lnx+elnx.

设g(x)=x+ex，则g′(x)=1+ex>0，所以g(x)单调递增，所以lna+x-1≥lnx，即x-lnx+lna-1≥0.

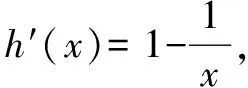
评析本题先把已知不等式变形为elna+x-1+(x+lna-1)≥lnx+elnx，从而具备ea±a≥elnb±lnb的同构形式，构造函数g(x)=x+ex，然后利用导数法求解结果，而此处难点在于将原不等式同解变形成左右两边具有相同“结构”的不等式.对原不等式同解变形，如移项、通分、取对数、系数升指数等，有时也需要对两边同时加、乘某式等，把不等式转化为左右两边是相同结构的式子，再根据“相同结构”构造辅助函数.

练习1.已知函数f(x)=aeax+1-lnx+1，且对任意x>1，f(x)>0恒成立，则a的取值范围是( ).

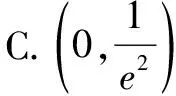
2.若关于x的不等式ex-alnx≥a恒成立，则实数a的取值范围为____.

3.对于任意实数x>0，不等式2ae2x-lnx+lna≥0恒成立，求实数a的取值范围是____.