核心素养视角下一道椭圆试题的探究

罗文军

(甘肃省秦安县第二中学 741600)

以直线与圆锥曲线的位置关系为背景考查三角形面积问题和定值问题是近几年高考和各类模考试题中的热点题型，这类试题可以很好地考查数形结合思想、分类讨论思想和函数与方程思想，可以很好地考查逻辑推理能力和运算求解能力等关键能力，可以很好地考查数学运算、逻辑推理和直观想象等数学学科核心素养.下面选取了一道关于椭圆内接三角形面积和定值问题的模考试题进行解法探究和拓展探究.

一、题目呈现

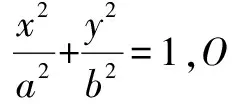
(1)求椭圆方程；

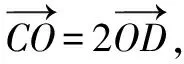
这道试题第(1)问考查了椭圆的几何性质，第(2)问考查了椭圆的内接三角形面积和向量的综合应用.

二、题目解析

1.第(1)问解析

评注根据椭圆的长轴长和离心率的定义，将已知条件代入解出长半轴长和半焦距的值，再根据b2=a2-c2解出b2值，从而得出椭圆标准方程.

2.第(2)问解析

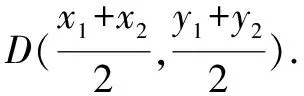
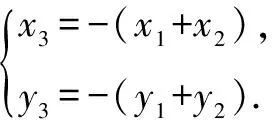
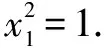
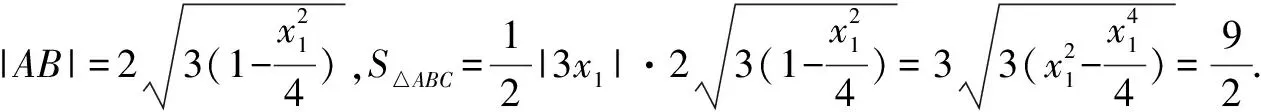
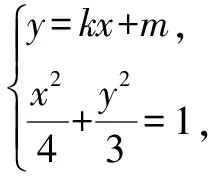
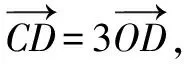
评注根据中点坐标公式和向量的坐标运算表示出点C的坐标，把AB看成△ABC的底边，再分直线AB斜率不存在和存在两种情况计算△ABC的面积，特别地，当直线AB斜率存在时，联立直线AB和椭圆方程，表示出两根之和与两根之积，表示出弦长|AB|和点C的坐标，再运用整体代换的思想可求出△ABC的面积.

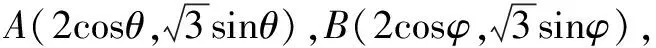
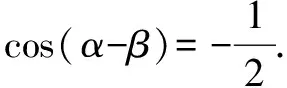
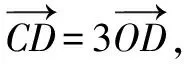
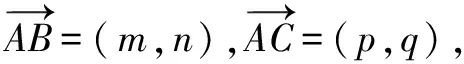
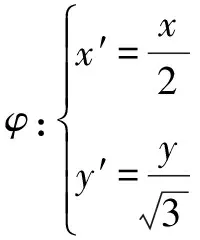
三、题目拓展

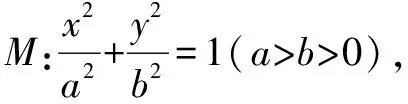
本文从多视角对例题进行多解探究，在习题教学实践中这样做有利于启发学生运用发散思维思考问题，为学生学会解题方法提供多样化选择，也有利于培育学生的创新意识和科学探索精神，有利于促进学生深度学习，有利于发挥模考题的最大功效，激发学生的学习兴趣，打破题海战术形成的思维定势.通过对这道圆锥曲线的多解探究，也提升了学生的数学运算、逻辑推理和直观想象等数学学科核心素养.