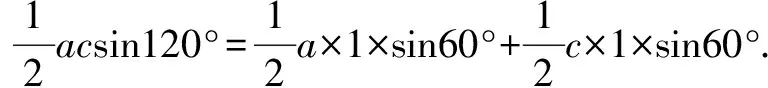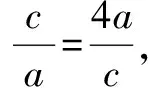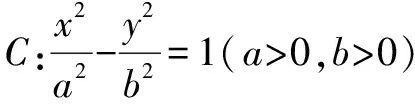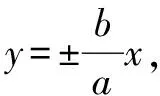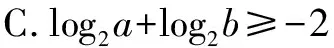基本不等式在解题中的应用
2021-12-26廖永福
廖永福
(福建省厦门第二中学 361009)
基本不等式结构简单,形式优美,它是高中数学的重要内容,也是高考数学的重要考点.应用时要依次满足条件:一正、二定、三相等,三者缺一不可.基本不等式是解决最值问题的有力工具,在解题中有着广泛的应用.
一、求最值
例1 (2020·江苏)已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是____.
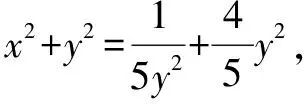
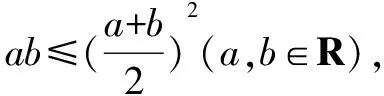
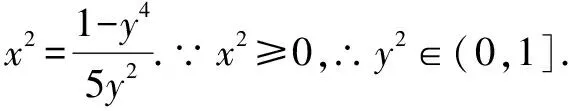
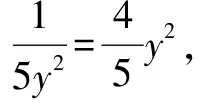
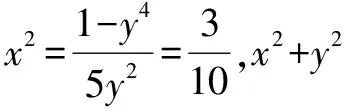
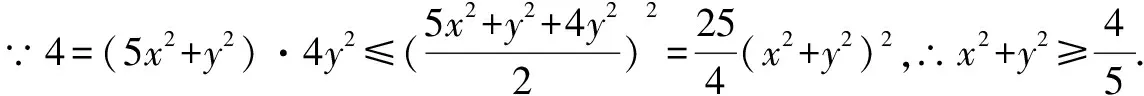
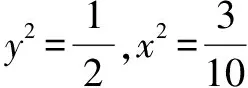
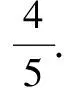
点评本题考查应用基本不等式求最值,考查转化思想和运算能力.解法一思路朴实,过程直接.解题关键是消元.把目标代数式表示成关于y的函数,直接应用基本不等式求解;解法二构思巧妙,方法灵活,解题关键是由条件等式构造出两个正数5x2+y2与4y2之积为定值,进而可用基本不等式的变式求解,属于中档题.
二、证明不等式
应用基本不等式证明不等式,常常与分析法、综合法、作差(商)法等结合使用,解题关键依然是构造两个正数之和(积)为定值,使之符合基本不等式的三个条件.
例2 (2020·全国卷Ⅲ(理))设a,b,c∈R,a+b+c=0,abc=1.
(1)证明:ab+bc+ca<0;
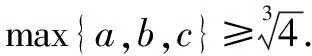
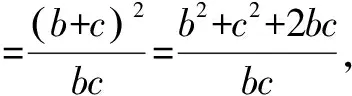
解答(1)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=0,
∵abc=1,∴a,b,c均不为0,则a2+b2+c2>0,
(2)不妨设max{a,b,c}=a,由a+b+c=0,abc=1可知,a>0,b<0,c<0.
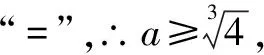
点评本题主要考查不等式的性质以及基本不等式的应用,属于中档题.
三、恒成立问题
对于含参数的不等式恒成立问题,常常将它转化为函数的最值问题求解.常用的结论有:(1)任意x∈D,f(x)>m恒成立⟺f(x)min>m;(2)对任意x∈D,f(x) 点评本题考查绝对值不等式,考查不等式恒成立问题的解法,考查二次函数最值的求法,考查利用基本不等式求函数的最值.解题关键是如何把不等式恒成立问题转化为函数的最值问题,属中档题. 应用基本不等式解决实际问题时,一般把要求最值的变量定义为因变量,根据实际问题抽象出函数的解析式后,利用基本不等式求出函数的最值,注意检验解是否在定义域内. 例4 (2017·江苏)某公司一年购买某种货物600吨,每次购买x吨,运费为6万元/次,一年的总存储费用为4x万元.要使一年的总运费与总存储费用之和最小,则x的值是____. 点评本题考查基本不等式的实际应用,考查推理与运算能力,属中档题. 与其它知识点交汇的问题是高考的热点,解决这类问题一般从这些知识点出发,建立变量之间的等量关系,再选用适当的方法求解. 例5 (2018·江苏)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为____. 分析根据面积关系建立a,c的方程,再用基本不等式求解. 点评本题考查三角形的面积公式,考查基本不等式的应用,利用常数代换法是解决本题的关键,属中档题. A.4 B.8 C.16 D.32 分析根据双曲线的渐近线方程求出点D,E的坐标,根据△ODE的面积为8,可得ab的值,再结合基本不等式,即可求得答案. 点评本题主要考查双曲线的性质和渐近线方程,考查基本不等式的应用,解题关键是应用a2+b2≥2ab建立双曲线的焦距与△ODE的面积之间的关系,属于中档题. 从上述例子可以看出,应用基本不等式解题要注意以下两点:一是注意基本不等式成立的条件;二是合理构造基本不等式中的和或积. 练习 1.(2020·海南)已知a>0,b>0,且a+b=1,则( ). (1)如果不限定车型,l=6.05,则最大车流量为____辆/小时; (2)如果限定车型,l=5,则最大车流量比(1)中的最大车流量增加____辆/小时. 5.(2020·全国卷Ⅱ(理))△ABC中,sin2A-sin2B-sin2C=sinBsinC. (1)求A;(2)若BC=3,求△ABC周长的最大值.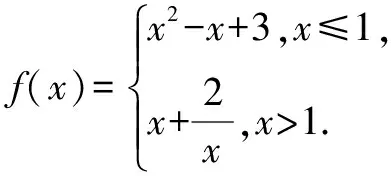
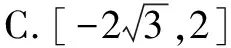
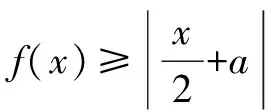
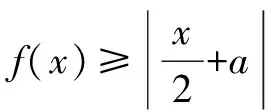
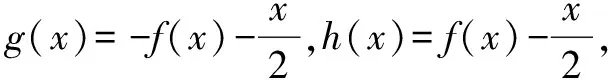
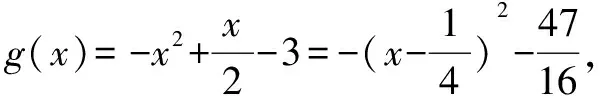
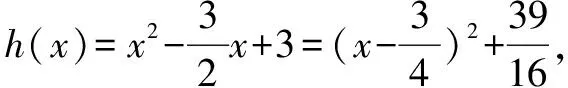
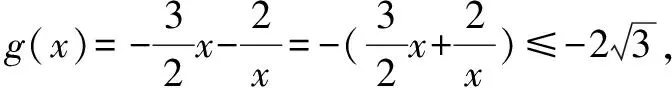
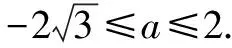
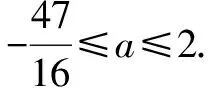
四、实际问题
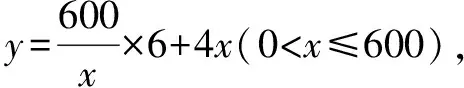
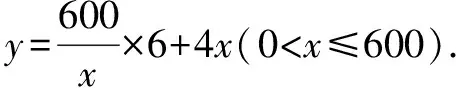
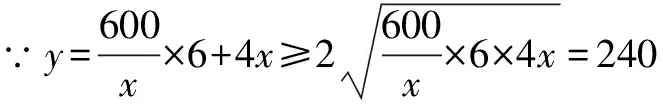
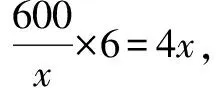
五、与其它知识点交汇的问题