动点轨迹方程问题的解法探讨

赵 林

(江苏省句容中等专业学校 212400)

动点的轨迹方程是解析几何的重要知识点，也是高考数学中的常见题型，求动点的轨迹方程需要运用代数、几何、三角等有关数学知识，本人结合自己的教学实践，将动点轨迹方程的一般解法归纳如下.

一、直接法

根据题目中的已知条件直接找到动点所满足的等量关系，从而写出含有变量x,y的等式，这种求轨迹方程的方法叫做直接法.

例1已知动点P到直线x=4的距离是它到点Q(1,0)的距离的2倍，求动点P的轨迹方程.

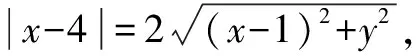
变式1已知动点P与平面上两定点A(-2,0),B(2,0)连线的斜率的积为4.求动点P的轨迹方程.

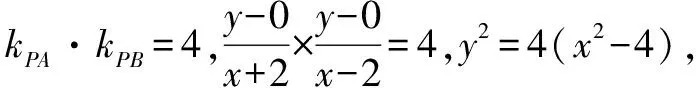
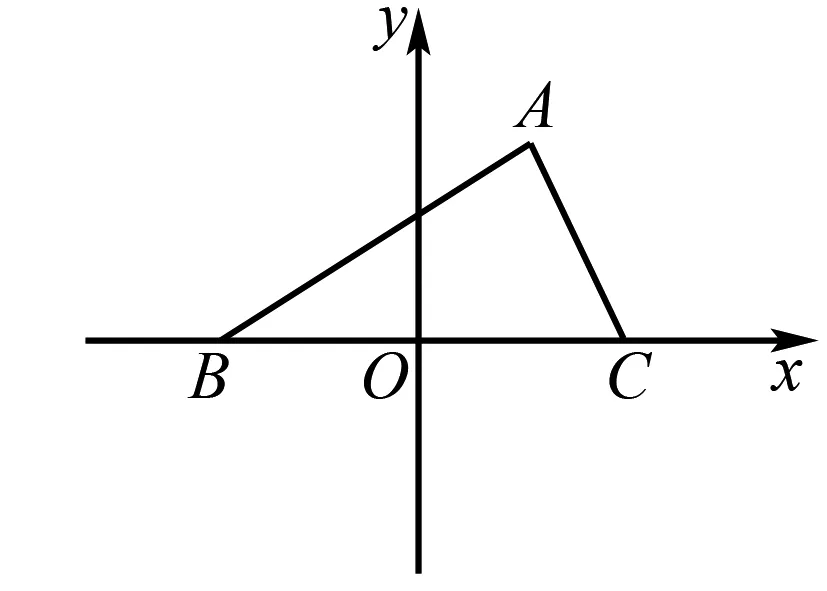
图1

变式2在△ABC中，已知点B(-3,0)和C(3,0)，动点A满足∠ACB=2∠ABC，求动点A的轨迹方程.

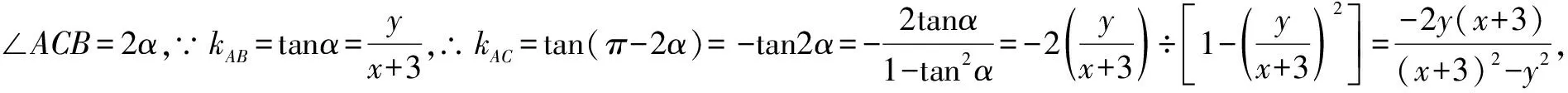
点评这一类题目比较简单，可以直接根据题目中的等量关系写出含有x,y的等式，然后两边再进行化简，就能得到所求动点的轨迹方程.

二、定义法

若动点的轨迹符合我们所学过某种已知曲线的定义，则可以利用曲线的定义写出其方程，这种求轨迹方程的方法叫做定义法.

例2已知圆P经过点N(2,0)，且与圆M：(x+2)2+y2=36相内切，求圆心P的轨迹方程.

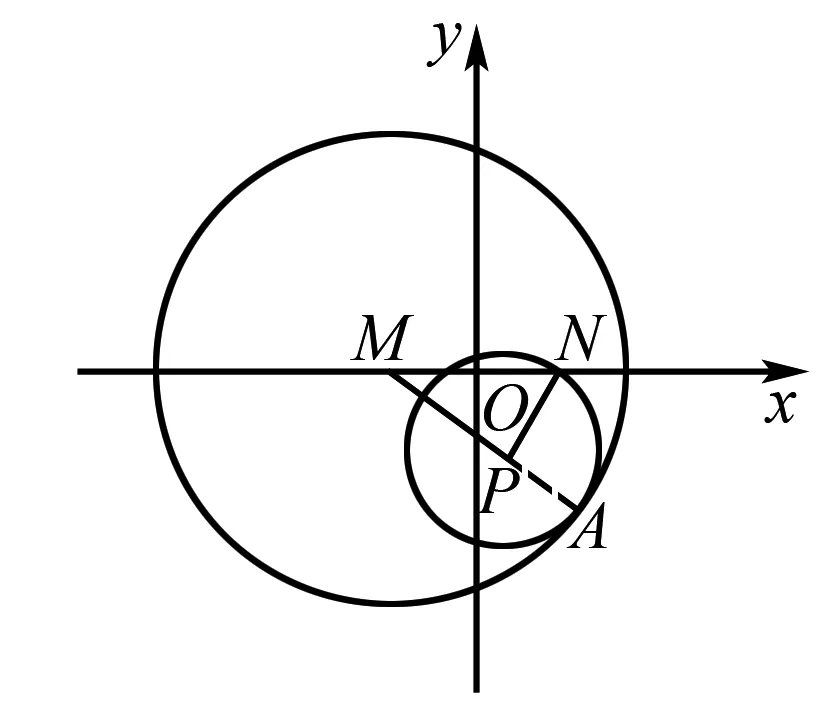
图2

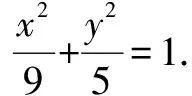
变式1若点M到点F(2,0)的距离比它到直线x=-3的距离小1，求点M的轨迹方程.

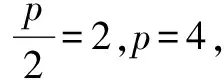
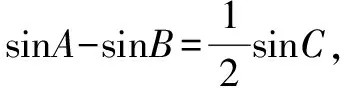
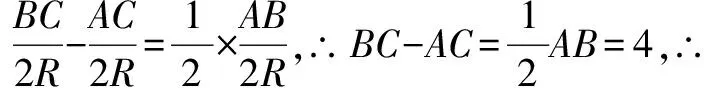
点评有些轨迹方程用直接法来做计算比较繁琐，可根据条件推导出动点的轨迹是所学过的已知曲线，这样就可以把轨迹问题转化为求曲线方程的问题.

三、几何法

根据平面几何的有关定理和性质推出动点所满足的等量关系，然后写出其轨迹方程，这种求轨迹方程的方法叫做几何法.

例3已知圆C：x2+y2+4x-12y+24=0，过点P(0,5)的直线与圆C交于M、N两点，求弦MN中点D的轨迹方程.

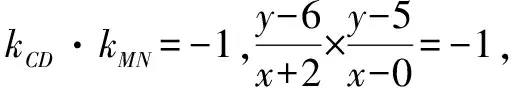
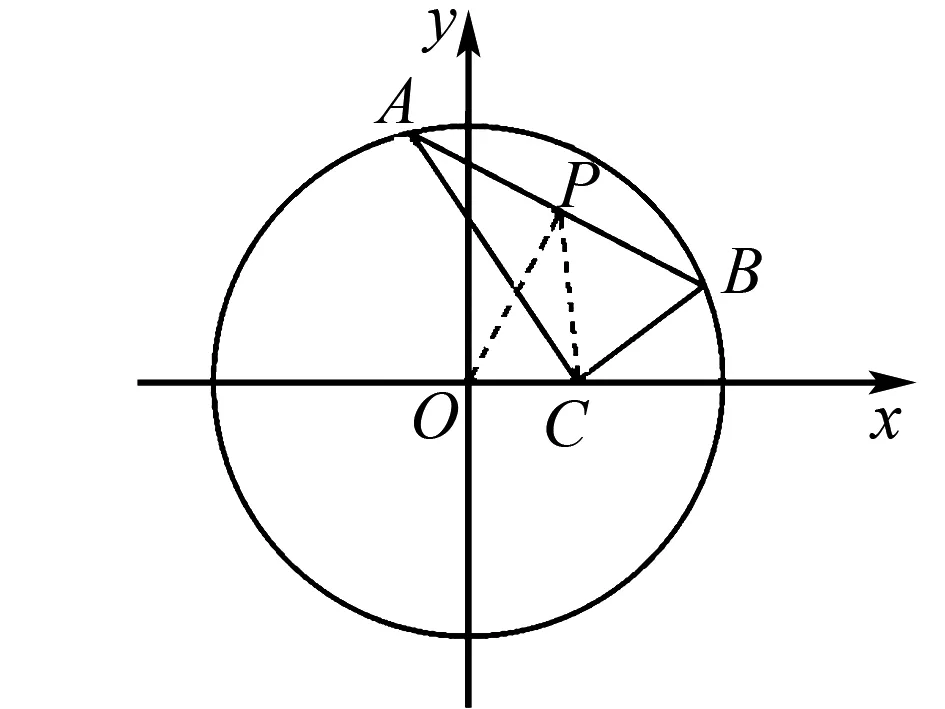
图3

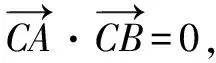
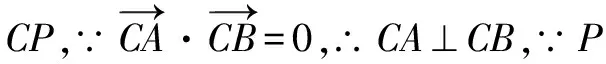
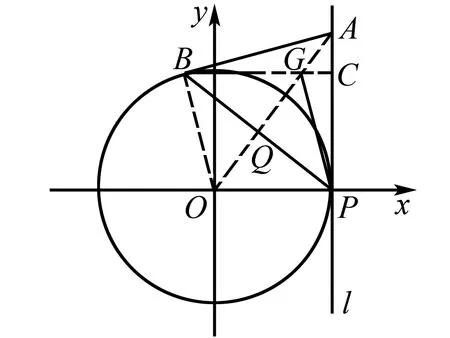
图4

变式2已知圆O：x2+y2=16与x轴的正半轴交于P点，过点P作圆O的切线l，在l上任取一点A，AB切圆O于点B，求ΔPAB的垂心的轨迹方程.

解设OA交PB于点Q，作BC⊥PA于点C，交OA于点G，则点G为△PAB的垂心.由切线长定理得：AB=AP，且OA垂直平分PB，由此得到GB=GP，∵OP∥BC，∴∠OPB=∠GBP=∠GPB，可以证明：Rt△OPQ≌Rt△GPQ，∴GP=OP=4，∵点P的坐标是(4,0)，所以△PAB的垂心的轨迹方程是(x-4)2+y2=16(与x轴交点除外).

点评用几何法来求动点的轨迹方程需要画图来进行观察和思考，经过推理和证明找到题目中动点所隐藏的等量关系，这样就可以避免一些复杂的计算.

四、代入法

若动点P与已知曲线上的动点Q存在着某种关系，则可以把点Q的坐标用点P的坐标来表示，然后代入曲线的方程，这种求轨迹方程的方法叫做代入法.

例4已知点A在圆x2+y2=9上，点B的坐标是(6,0)，点P分AB之比为2∶1，求点P的轨迹方程.

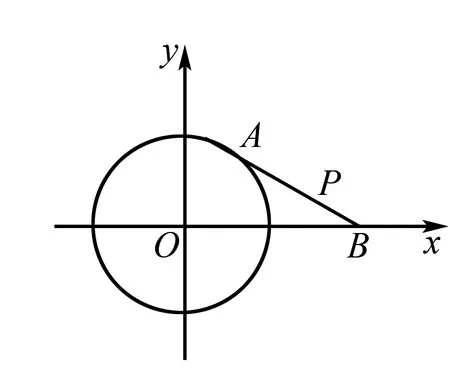
图5

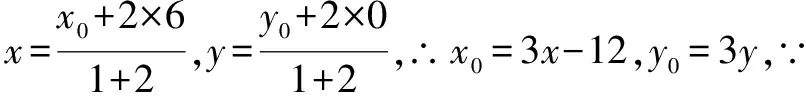
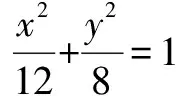
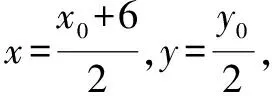
变式2过双曲线x2-y2=4上一点A作直线l：x+y=4的垂线，垂足为点B，求线段AB的中点M的轨迹方程.

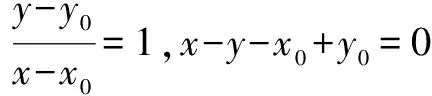
点评若动点P所满足的条件难以表达或求出，但却随着已知曲线上另一动点Q作有规律的运动，这时可以利用点P和点Q坐标之间的关系，求出动点P的轨迹方程.

五、参数法

有些题目可以借助参数，找到动点坐标x,y之间的等量关系，再从得到的等式中消去参数，就能得到轨迹方程，这种求轨迹方程的方法叫做参数法.

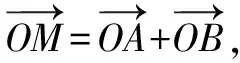
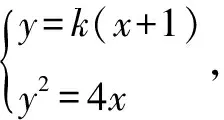
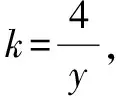
变式1已知圆C：x2+y2+2(m-1)x-4my+5m2-m-3=0，求圆心C的轨迹方程

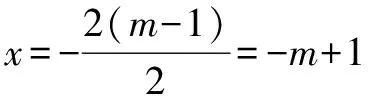
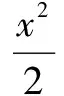
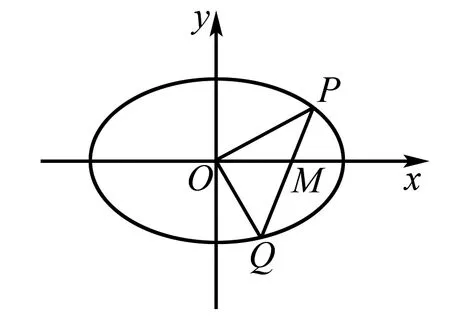
图5

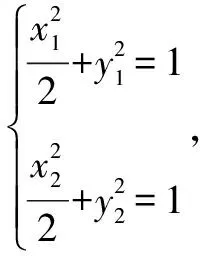
点评有些动点坐标x,y之间的关系不太容易发现，也很难判断动点符合某种已知曲线的定义，这时就可以引入参数，建立x,y之间的等式，从而使问题得到解决.