一个圆锥曲线问题的解决与推广

许银伙

(福建省泉州外国语中学 362000)

转化与化归是高中重要的数学思想方法，它对于问题的思路探寻和简化运算有着不可估量的作用.本文通过针对一个椭圆常规练习题的拓展探索，运用转化与化归思想，得出在圆锥曲线中同类问题的一般性结论.

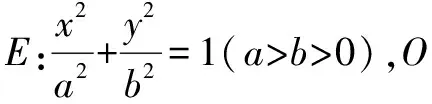
(1)求椭圆E的标准方程；

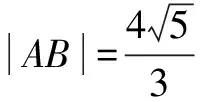
(3)在平面直角坐标系xOy中，若存在与点M不同的点G，使得|GA||MB|=|MA||GB|成立，求点G的坐标.

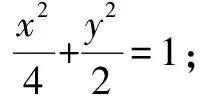
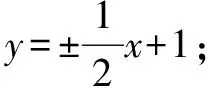
(3)设存在符合条件的点G，由已知条件和椭圆的对称性得点G必在y轴上，可设点G(0,y0)，A(x1,y1)，B(x2,y2).

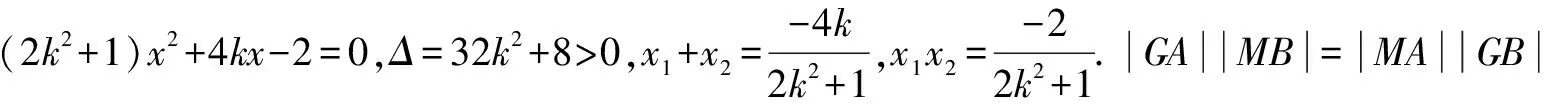
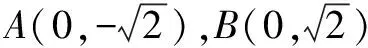
综上得，符合要求的点G存在，且点G的坐标(0,2).

评注问题(3)的解决诀窍是利用对称性判断出所求点G必须在y轴上，然后把距离的乘积转化为横坐标和斜率的比，使其到两个交点的连线斜率互为相反数，或者到两个交点连线的倾斜角互补，再利用韦达定理得出结果.

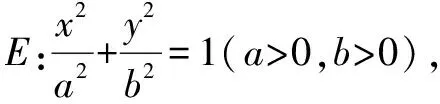
解析设存在符合条件的点G，由已知条件和曲线的对称性得点G必在y轴上，可设点G(0,y0)，A(x1,y1)，B(x2,y2).

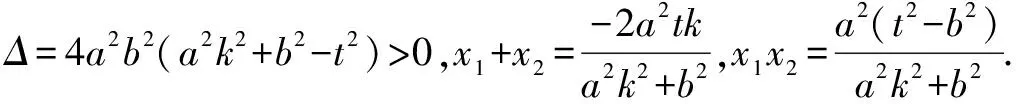
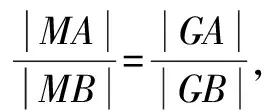
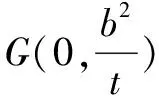
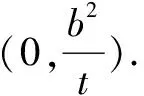
评注1.推广一把原来问题一般化，运用上面的方法和技巧获得一般化的结论.

2.曲线E可以是焦点在x轴或y轴上的椭圆，还可以是圆.

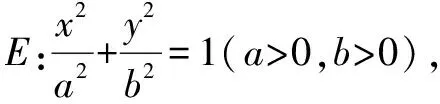
解析设存在符合条件的点G，由已知条件和曲线的对称性得点G必在x轴上，可设点G(x0,0)，A(x1,y1)，B(x2,y2).

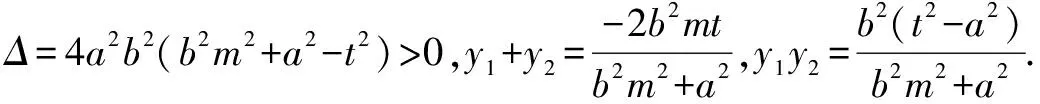
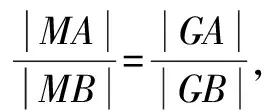
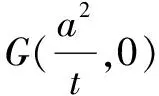
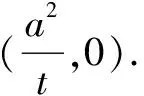
评注1.推广二只是把推广一中曲线内的定点放到曲线的另一对称轴，运用同样的方法和技巧获得一般化的结论.2.曲线E可以是焦点在x轴或y轴上的椭圆，还可以是圆.

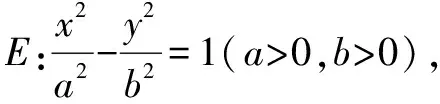
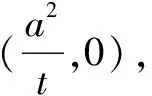
评注推广三只是把推广二中椭圆换成焦点在同一坐标轴上的双曲线，运用上面的方法和技巧获得一般化的结论.

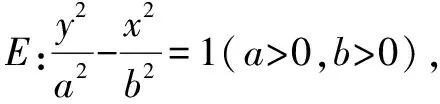
解析设存在符合条件的点G，由已知条件和双曲线的对称性得点G必在x轴上，可设点G(x0,0)，A(x1,y1)，B(x2,y2)，显然直线l的倾斜角不为0°.

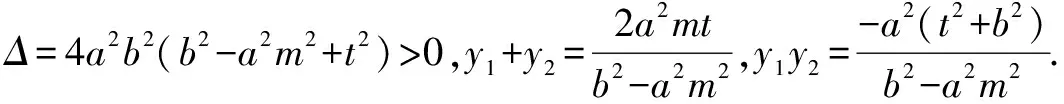
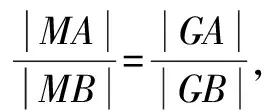
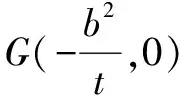
评注推广四把推广三的双曲线换成焦点在另一坐标轴上，运用上面的方法和技巧获得一般化的结论.

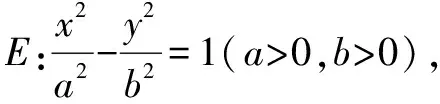
解析设存在符合条件的点G，由已知条件和双曲线的对称性得点G必在y轴上，可设点G(0,y0)，A(x1,y1)，B(x2,y2)，显然直线l斜率存在.

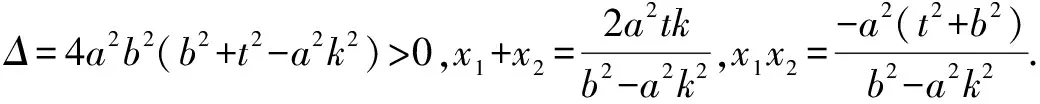
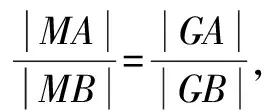
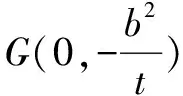
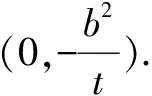
评注推广五把推广三中直线所过坐标轴上的定点换成另一坐标轴上，运用上面的方法和技巧获得一般化的结论.

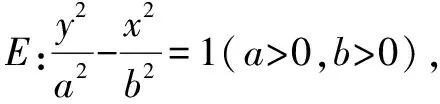
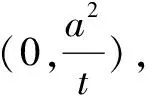
评注推广六把推广四中直线所过坐标轴上定点换成另一坐标轴上，运用上面的方法和技巧获得一般化的结论.

推广七已知抛物线E：y2=2px，过异于原点的定点M(t,0)的动直线l与抛物线E交于A,B两点，是否存在与点M不同的点G，使得|GA||MB|=|MA||GB|成立；若存在，求点G的坐标.

解析设存在符合条件的点G，由已知条件和抛物线的对称性得点G必在x轴上，可设点G(x0,0)，A(x1,y1)，B(x2,y2)，显然直线l的倾斜角不为0°.

①当直线l斜率存在时，设l方程：x=t+my，代入抛物线E得：y2-2pmy-2pt=0，由已知得：Δ=4p2m2+8pt>0，y1+y2=2pm，y1y2=-2pt.

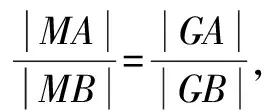
②当直线l斜率不存在时，由抛物线对称性得G(-t,0)符合|GA||MB|=|MA||GB|.

综上得：符合要求的点G存在，且点G的坐标(-t,0).

评注推广七把推广二中的曲线换成抛物线，运用上面的方法获得一般化的结论.

推广八已知抛物线E：x2=2py，过异于原点的定点M(0,t)的动直线l与抛物线E交于A,B两点，是否存在与点M不同的点G，使得|GA||MB|=|MA||GB|成立；若存在，求点G的坐标.

类似推广七得符合要求的点G存在，且点G的坐标(0,-t)，过程略.

评注1.推广八把推广七中抛物线对称轴改变，运用上面的方法和技巧获得一般化的结论.

2.推广七和八通常取定点M为抛物线的焦点作为质检考题.

见微知著，举一还三，是学好数学必需的能力与习惯，需要有意识的培养与磨练.本文通过针对一个普通练习题的拓展思考，获得同类问题的一般性结论，既强化问题解决的方法和技巧，又加深对问题的本质认识，值得在数学学习与研究的过程中借鉴.