基于H-MMC风力发电系统无差拍电流控制策略
2021-12-26荣飞潘烙徐爽杨光源周诗嘉
荣飞,潘烙,徐爽,杨光源,周诗嘉
(1. 湖南大学电气与信息工程学院,长沙410082;2. 中国南方电网超高压输电公司检修试验中心,广州510663;3. 南方电网科学研究院,广州510663)
0 引言
随着化石能源匮乏和环境污染问题日趋严重,新能源发电技术受到广泛关注,同时风电在电网中的渗透率也不断提高[1]。由于风机容量的不断扩大,风电变流器受开关器件的耐压等级的限制,目前多采用多电平的形式来实现大功率风机并网[2]。文献[3]采用了一种三电平背靠背二极管钳位型变流器,实现了中压风机并入三相交流电网。由于电平数较少,若要实现中高压需要额外接入变压器,从而增加了系统体积和成本[4]。文献[5]搭建了基于级联H桥(cascaded H-bridge,CHB)的多电平直驱永磁风力发电系统,CHB通过将多个耐压等级低的H桥串联起来实现高压输出,安装、维护简单。但每个子模块都需要配备独立的直流电源,且需设计相应容量的多绕组移相变压器,成本和系统体积太大。文献[6]采用背靠背模块化多电平变流器(back-to-back MMC,BTB-MMC)实现了直驱永磁风机并网。MMC是近年研究出的一种新型多电平拓扑。与传统两电平和三电平变流器相比,MMC具有输出电压等级高、功率器件应力低、冗余性好、可拓展性强的特点,无需变压器即可直接并网,已广泛应用于中、高压场合[7]。但MMC低频时存在子模块电容电压波动问题,可通过高频注入法和功率通道法解决该问题,前者会增加器件电流应力和系统损耗,后者会增加控制复杂度[8 - 10]。
文献[11]实现了基于模块化多电平矩阵变流器(modular multilevel matrix converter,M3C)的直驱永磁风力发电系统,M3C将常规的矩阵变流器中的全控双向功率器件替换成了全桥子模块串联而成的桥臂,也具有模块化多电平的特点,但内部环流通路较多,控制比较复杂[12]。
文献[13]提出了一种新型大容量模块化多电平六边形变流器。H-MMC结合了MMC和M3C的优点:具有模块化的结构的特点,便于生产、安装和维护;拓展性强,可通过改变子模块数量扩展至任意容量、电平数和电压等级,而且无需额外增加变压器即可并入交流电网;与BTB-MMC和M3C相比,桥臂数量减少一半,只需要6个桥臂就可以实现两个频率不同、幅值不同的交流系统能量的交换,而且省去了中间的直流环节,不存在直流故障问题。文献[14]比较了H-MMC与BTB-MMC桥臂能量波动情况,结果表明H-MMC在低频工况下优势更明显,因此非常适用于中压风力发电系统。
文献[15]通过H-MMC将3.3 kV、5 MW直驱永磁风机并入10 kV交流电网,采用了载波移相(carrier phase shift,CPS)的调制方式,需要对所有桥臂上的子模块进行单独的PI稳压控制,增加了处理器负担[16];在桥臂电流跟踪上采用双PR控制器,对机侧和网侧两种不同的频率分量分别进行了跟踪,但由于要配合多组PI调节器,PR参数难以整定,控制比较复杂,降低了系统的动态性能。文献[17]研究了在电网电压跌落至原来的40%后,通过利用H-MMC子模块分布式电容作为缓冲抑制无功二倍频波动、抑制负序电流波动和抑制有功二倍频波动,从而保证器件不会过流,在电网故障消除后能够在0.2 s内达到稳态。
基于以上问题,本文将采用基于无差拍电流控制的方式,不用考虑机侧频率和网侧频率的影响,能够对桥臂电流进行快速跟踪;再配合最近电平逼近调制方式,通过排序法免去了单个子模块电容电压平衡的控制,降低了系统控制复杂度。
1 系统拓扑结构与数学模型
基于H-MMC的风力发电系统如图1所示,系统包括一个六边形变流器,该变流器由6个相同的桥臂组成,每个桥臂由N个全桥子模块和1个电感L串联而成。永磁同步发电机三相A、B、C 和电网的三相 U、V、W 交替地连接到相邻两桥臂连接点上。

图1 基于H-MMC的风力发电系统结构图Fig.1 Structure diagram of wind power generation system based on H-MMC
将H-MMC每个桥臂上的级联子模块等效为一个电压源,忽略机侧的滤波电容Cf和网侧的滤波电感Lf,则上述系统可以等效为如图2所示的简化电路。
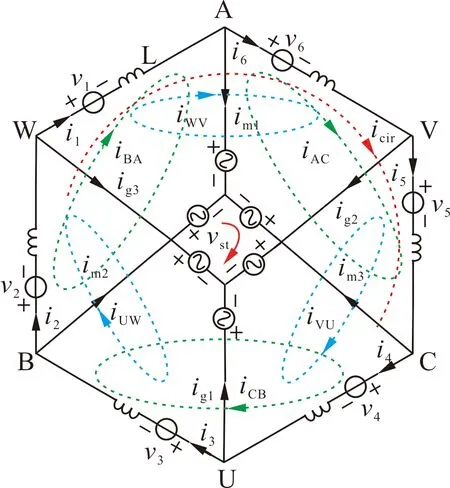
图2 H-MMC简化电路Fig.2 Simplified circuit of H-MMC
图2中,vx、ix(x=1,2,3,…,6)分别为6个桥臂上的电压和电流,vmi、imi(i=1,2,3)分别为机侧A、B、C三相电压和电流,vgj、igj(j=1,2,3)分别为网侧U、V、W三相电压和电流,vst为中性点电压。
根据基尔霍夫电压定律可以得出各桥臂电压与机侧、网侧电压之间的数学关系为:
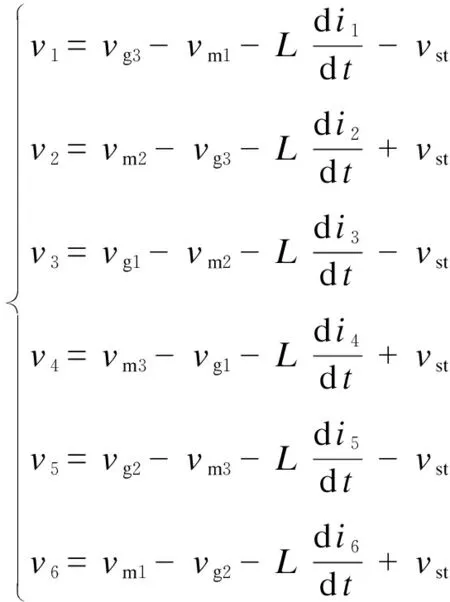
(1)
再根据网孔电流法分析可得各桥臂电流与机侧、网侧电流之间的数学关系为:
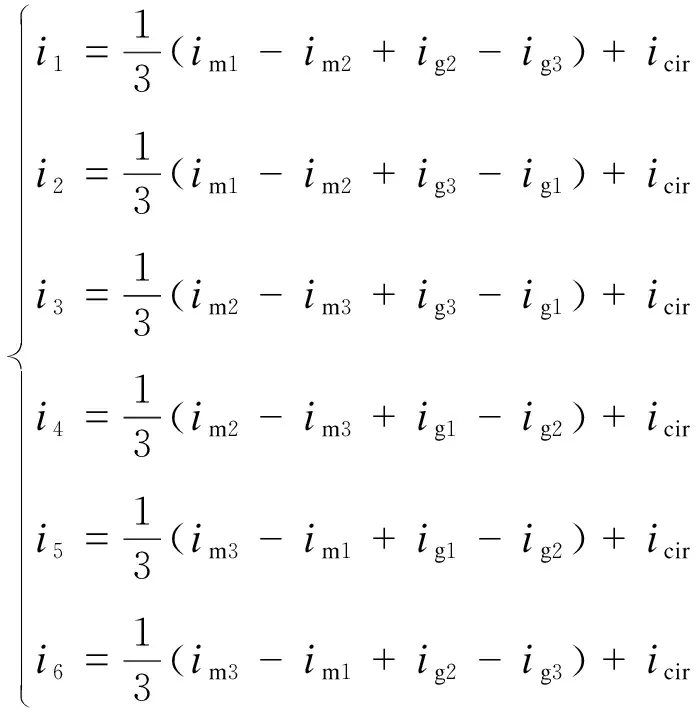
(2)

表1 风力发电系统不同变流器之间的对比Tab.1 Comparison among different converters of wind power system
式中icir为桥臂环流。
由式(1)和式(2)可知,桥臂电压中包含机侧频率电压分量、网侧频率电压分量以及中性点电压分量;桥臂电流含有机侧频率电流成分、网侧频率电流成分和环流,因此若要对该风电系统进行控制,则需要对各成分分别进行相应分析计算。
2 H-MMC与已有变流器的比较
变流器是风力发电系统的重要组成部分,根据风力发电机输出电压等级不同,将变流器分为低压和中压变流器,适用于1 kV以下的变流器为低压变流器,适用于1~35 kV的变流器为中压变流器。表1为风力发电系统不同变流器之间的对比。
如表1所示,H-MMC适用于中压场合,与已有的变流器相比,只需6个桥臂即可实现AC/AC变换,无需升压变压器,成本较低。此外,H-MMC的低频特性优势明显,器件的电压应力较低,通过多电平技术提高等效开关频率从而实现较好的输出电能质量。
3 控制策略
3.1 MPPT控制
为提高风能利用率,对风机采用最大功率跟踪(MPPT)控制。转速参考值ωref(K)可以通过式 (3) 计算得到。
(3)
式中:ωref(K)为转速参考值;λs为最佳叶尖速比;v(K)为当前时刻风速;R为风机叶片半径。
对风机采用id=0的控制方式,即将d轴分量参考值imd_ref(K)设为0,q轴分量参考值imq_ref(K)通过将参考转速和实际转速作差后经过一个PI调节器得到:
(4)
式中:ω(K)为风机实际转速;KP1、KI1分别为第1个PI控制器的比例系数和积分系数。
机侧三相参考电流imi_ref(K)可由dq轴参考电流imd_ref(K) 、imq_ref(K)进行dq/abc变换得到。
3.2 网侧控制
由于网侧电压为一恒定值,当外界风速波动的情况下,风机的输出功率也会产生波动,需要实时调整网侧电流以满足有功平衡。
同理,网侧电流也先控制dq轴电流igd、igq,本文采用网侧功率因数为1的运行控制方式,即q轴电流参考值igq_ref(K)为0。d轴电流参考值igd_ref(K)可通过将子模块电容电压参考值和所有桥臂电容电压平均值作差经过一个PI控制器得到:
(5)
式中:UC_ref(K)为子模块电容电压参考值;UC_av(K)为变流器所有子模块电容电压平均值;KP2、KI2分别为第2个PI控制器的比例系数和积分系数。
3.3 子模块电容电压均衡控制
文献[15]指出,变流器桥臂x中常量功率Px_const会造成桥臂能量累积,需要注入常数环流和中性点电压来补偿系统无功,将其控制为0,具体为:
(6)
式中:Pm、Pg分别为风机发出的有功和电网吸收的有功,Qm、Qg分别为风机发出的无功功率和电网吸收的无功功率。
当电网吸收的无功为0时,则注入的常数环流参考量icir1_ref以及中性点电压参考量vst_ref满足:
(7)
图3为H-MMC简化等效电路。因此,式(7)中的icir1_ref(K)与中性点电压参考值vst_ref(K)可以通过控制奇、偶桥臂间的有功功率得到,具体如式(8)—(9)所示。
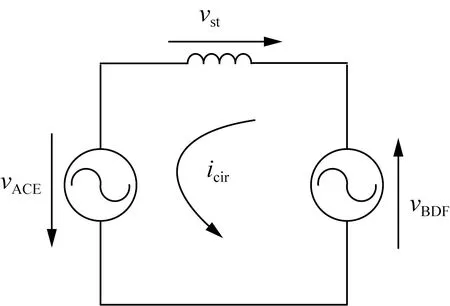
图3 H-MMC简化等效电路Fig.3 Simplified equivalent circuit of H-MMC
(8)
(9)
式中:UC1,3,5_av(K)、UC2,4,6_av(K)分别为第K个控制周期变流器奇数桥臂和偶数桥臂电容电压的平均值;KP3、KI3、KP4、KI4分别为第3个PI控制器和第4个PI控制器的比例系数和积分系数。
实际系统中,桥臂环流中除了直流分量icir1外,还存在交流分量icir2。这是由于系统运行时,桥臂的能量总是会存在偏差,在控制奇数桥臂和偶数桥臂能量平衡的基础上,还需控制各个桥臂子模块电容电压平衡。本文采用注入交流环流的方法,其交流分量参考值icir2_ref(K)为:
(10)
式中:vbx(K)为桥臂x的输出电压;UCx_av(K)为桥臂x子模块电容电压的平均值;KP5为第5个P控制器的比例系数。
将环流直流分量参考值与交流分量参考值相加即可得到总的环流参考值icir_ref(K)。
icir_ref(K)=icir1_ref(K)+icir2_ref(K)
(11)
3.4 桥臂电流无差拍控制
无差拍控制的思路为:根据系统的反馈信号和状态方程以及下一控制周期的输出参考量来计算下一时刻的开关状态。具有一拍即达的特性,能够实现快速跟踪。将计算得到的机侧电流参考值和网侧电流参考值以及环流参考值代入式(2),计算出桥臂电流参考值。
(12)
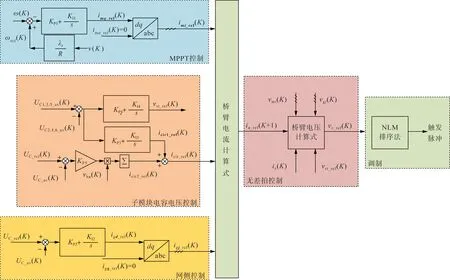
图4 风电系统直接AC/AC并网控制框图Fig.4 Control block diagram AC/AC connection grid of wind power system
式中:ix_ref(K)为第K个控制周期桥臂x的电流参考值;imi_ref(K)为第K个控制周期机侧A、B、C三相电流参考值;igj_ref(K)为第K个控制周期网侧U、V、W三相电流。
为了进一步提高控制准确性,对ix_ref进行预测,第K+1个控制周期的桥臂电流参考值ix_ref(K+1)为:
ix_ref(K+1)=2ix_ref(K)-ix_ref(K-1)
(13)
根据式(12)和式(13),对桥臂电流进行无差拍跟踪控制,代入式(1)后可得:
(14)
式中:vx_ref(K)为第K个控制周期桥臂x的电压参考值;T为控制周期;vmi(K)为第K个控制周期机侧A、B、C三相电压,通过实际测量得到;vgj(K)为第K个控制周期网侧U、V、W三相电压,由式(15)得到。
本文采用最近电平逼近的调制方式得到各个桥臂上子模块的控制信号,同时通过排序法可实现单个子模块电容电压的平衡。图4为本文所提风电系统直接AC/AC并网的总体控制框图。
式中:vg1,2(K)、vg2,3(K)、vg3,1(K)为网侧U、V、W三相之间的线电压。
4 仿真分析
为了验证本文所提出的控制方法的有效性,本节根据MHI Vestas的V164- 10MW海上风电机组参数,在MATLAB/Simulink中搭建了如图1所示的基于H-MMC的10 MW直驱式永磁同步风力发电系统模型。仿真参数如表2所示。
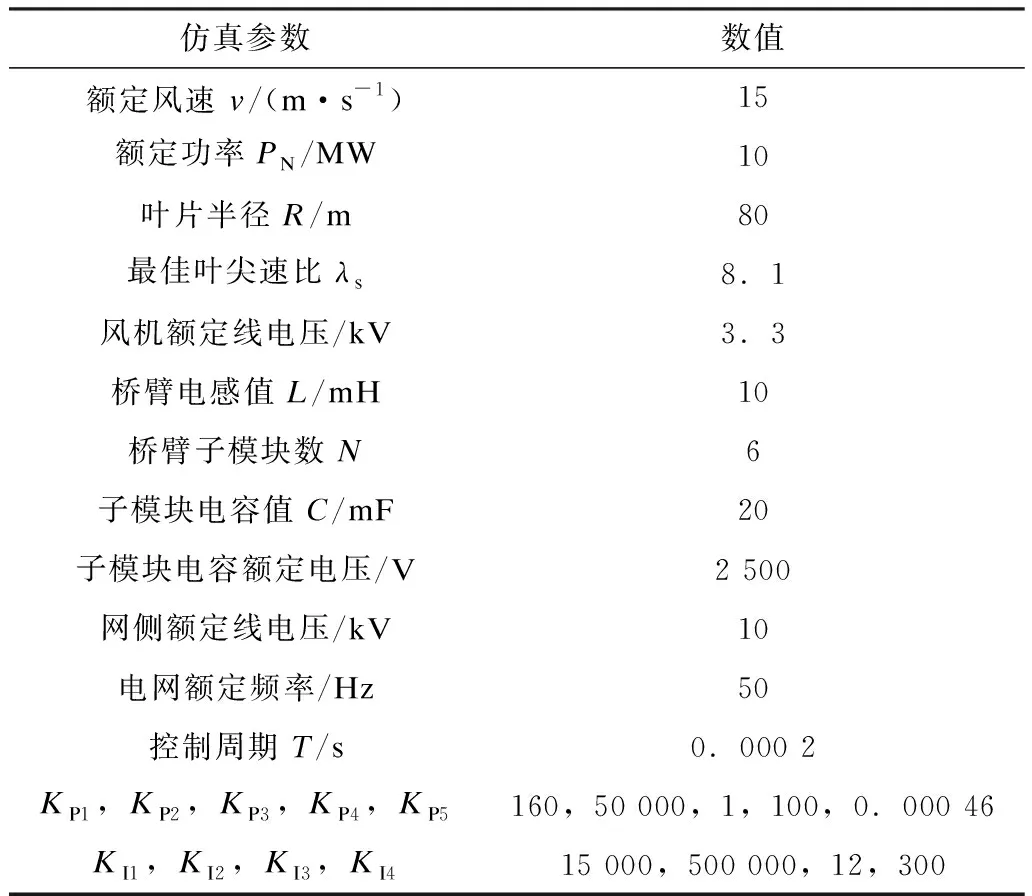
表2 仿真参数Tab.2 Simulation parameters
4.1 稳态仿真
在额定风速下进行稳态仿真分析,分别采用无差拍(deadbeat)控制方法和双PR控制的仿真结果如图5所示。

图5 稳态仿真结果Fig.5 Steady state simulation results
图5(a)—(d)分别为两种控制方法下的机侧电流和网侧电流,幅值分别为2 601 A、810.1 A。当采用双PR控制时,机、网侧电流谐波畸变率分别为4.14%、8.81%。当采用无差拍控制时,傅里叶分析可知,其谐波畸变率分别为1.01%、2.18%,相比电流谐波畸变率分别减少了3.13%和6.63%,满足电网并网标准(总谐波畸变率≤5%)。可见在额定风速下采用无差拍控制风机并网质量优于传统控制方法。
图5(e)、(f)分别为两种控制方法下的桥臂电流跟踪情况。桥臂电流幅值为2 080 A,采用双PR控制时瞬时最大跟踪偏差为150 A,采用无差拍控制时最大偏差为100 A,相比减小了50 A,因而无差拍控制具有更高的控制精度。
图5(g)、(h)分别为两种控制方法下的桥臂1上子模块电容电压。采用双PR控制时,子模块电容电压在2 600~2 250 V内波动,纹波为14%;采用无差拍控制时,子模块电容电压在2 580~2 370 V内波动,纹波为8.4%,相比减少了5.6%。
4.2 动态仿真
为观察风速发生突变时,两种控制方法下的动态跟踪性能,设定在t=0.3 s时风速从额定风速在0.025 s内下降到11.3 m/s,对系统进行动态仿真分析,结果如图6所示。
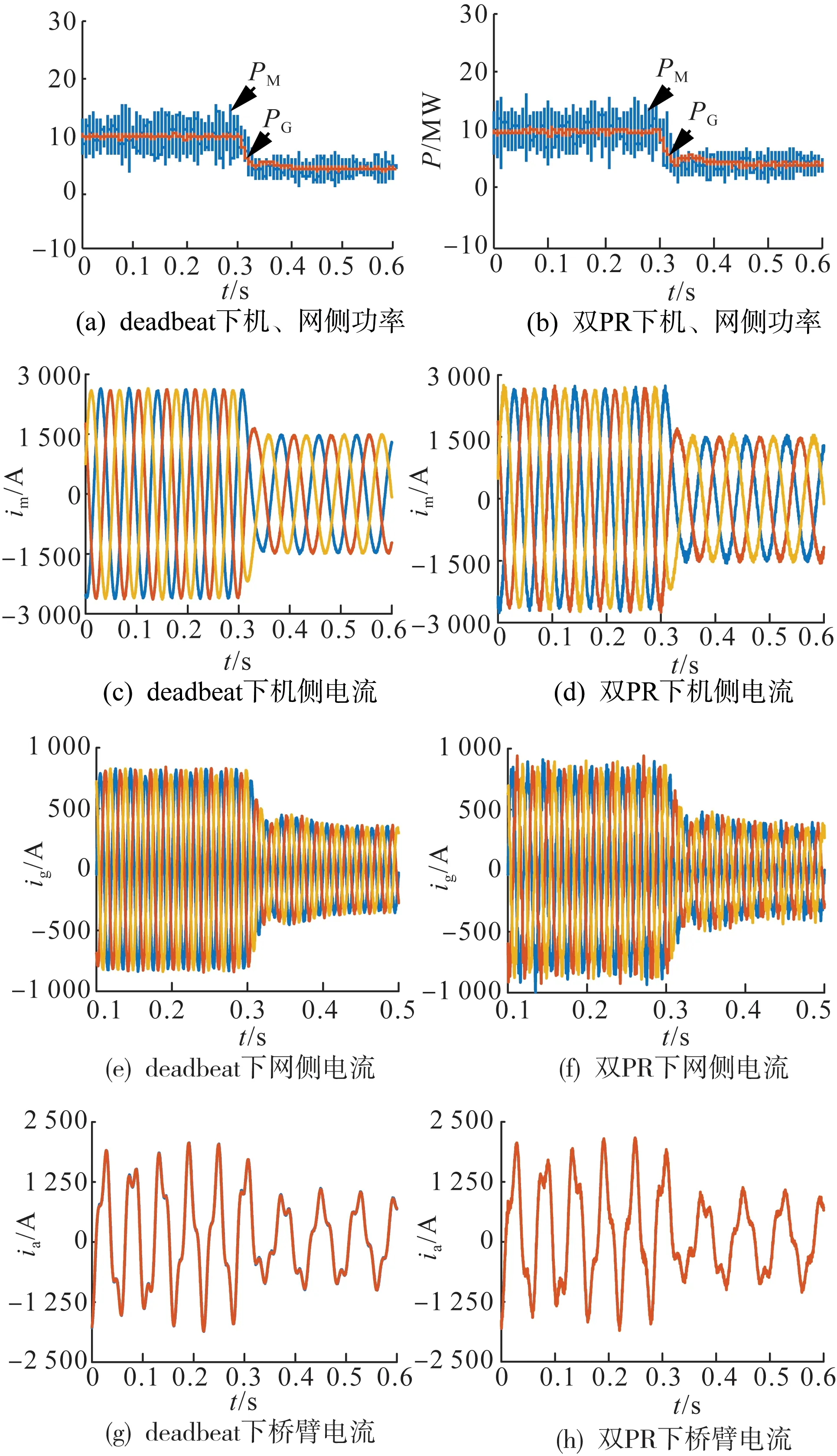
图6 动态仿真结果Fig.6 Dynamic simulation results
图6(a)、(b)分别为两种方法下风机输出功率和电网吸收功率。两种方法下,输入、输出功率基本都维持在10 MW左右。但分析结果可知,采用无差拍控制时的功率波动略小,表明系统损耗较低。
图6(c)—(f)分别为风速变化时两种控制方法下的机侧电流和网侧电流。风速变化后,幅值分别为1 461 A、346.8 A。当采用双PR控制时,机、网侧电流谐波畸变率分别为3.92%、15.53%。采用无差拍控制时,傅里叶分析可知,其谐波畸变率分别为1.42%、4.42%,相比电流谐波畸变率分别减少了2.5%和11.11%。由此可以看出无差拍控制应对外界干扰能力比较强,受机侧频率变化影响较小。
图6(g)、(h)分别为风速变化时两种控制方法下的桥臂电流跟踪情况。风速变化后,桥臂电流幅值为1 100 A,采用双PR控制时瞬时最大跟踪偏差为150 A,采用无差拍控制时最大偏差为65 A。从中可以看出采用无差拍控制方法,风速发生变化后,其跟踪误差也会明显减小以达到高跟踪精度,但传统控制方法下,跟踪误差基本不变,从而导致系统输入功率降低后,输出电流谐波含量较大。因而无差拍控制具有更高的控制精度。
5 结语
随着风机装机容量的不断增大,对其并网变流控制提出了更高的要求。H-MMC低频特性优势明显,但国内外鲜有研究将H-MMC应用于风力发电领域。本文在现有研究基础上提出了将无差拍电流控制应用于基于H-MMC的直驱式永磁同步发电系统。通过分析桥臂电流、电压和机侧与网侧之间的耦合关系,设计出了无差拍的桥臂电流内环和桥臂电压的电压外环。与双PR控制方法相比,简化了系统控制复杂度,而且无差拍不受两侧交流频率波动的影响,因此在风速波动的情况下也能快速响应。另一方面,将无差拍控制与NLM调制方式相结合,能够实现在开关频率低的情况下仍能保持谐波含量少。需要说明的是,无差拍控制受参数影响较大,因而需要进行相应的模型预测,笔者所在实验室将会对此进行进一步研究。
