基于熵产的旋流泵流动损失特性分析

赵凯尧，刘厚林*，杜振明，谈明高，胡胜，董亮

(1. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013； 2. 大连利欧华能泵业有限公司，辽宁 大连 116049)

旋流泵是一种无堵塞性能良好的固液两相流泵，具有结构简单、制造方便等优点，因此被广泛应用于含有纺织物、皮毛、碎木屑及纸浆等复杂介质的输送场合[1-2].不同于一般的离心泵结构，旋流泵的叶轮后退至后泵腔内，叶轮与蜗壳前盖间有着较大的轴向空间，因此泵内流动特性非常复杂，存在着贯通流、循环流以及不同的其他涡结构.旋流泵的水力损失大，效率偏低，大多数旋流泵的效率都在60%以下[3-5].目前对于旋流泵流动损失的研究仍不完善，尤其是当其工作于非设计工况时，有时会产生剧烈的不稳定流动，这将导致旋流泵内部的能量损失增大，产生高分贝的运行噪声和大幅度的泵体振动，严重时甚至会造成泵机的损坏[6-7].所以对旋流泵运行过程中的内部流场特性以及流动损失进行研究显得尤为重要.

由于流场的复杂性，水泵的流动损失特性难以直接通过试验手段获得[8].张永学等[9]借鉴已经在流动传热设备中成功应用的熵产分析方法，对离心泵运行过程中的能耗损失进行评价，并与传统评价方法进行比较，验证了该方法的可行性.张帆等[10]通过理论和数值方法计算流动过程中的熵产，定性分析了侧流道泵流动损失的特点.王延锋[11]基于熵产理论对径向式导叶多级泵进行性能优化，优化后流动损失减小，有效地改善了泵内的流动情况.CFD技术的成熟发展为基于熵产理论的流动评价方法提供了更为直观准确的表征方式[12].

文中以旋流泵为研究对象，基于熵产理论探究旋流泵的能量损失特性，并通过数值模拟对各个过流部件的内流特征进行分析，确定流动损失的具体位置，为旋流泵的优化设计提供依据.

1 熵产理论

熵产理论来源于热力学第二定律，通过对旋流泵过流部件的熵产计算，可以直观表征流动不稳定的区域，定量描述流场内的能量损失.泵内熵产形式可分为4种：直接耗散熵产、湍流耗散熵产、平均温度梯度熵产、脉动温度梯度熵产[9].水泵在纯水介质下工作，由温度变化产生的熵产比例较小，可以忽略内部的热量交换.因此，文中讨论旋流泵在运行过程中的流动熵产时只考虑直接耗散熵产和湍流耗散熵产.

由平均速度产生的熵产率(直接耗散熵产率)计算公式为

(1)

由脉动速度产生的熵产率(湍流耗散熵产率)计算公式为

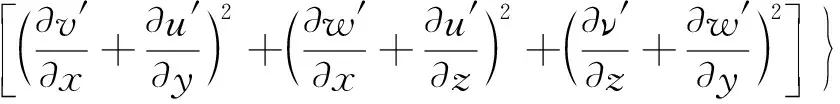
(2)

式中：μ为流体动力黏度；u，v，w分别为质点当地速度在直角坐标系下的3个分量;T为流体质点的当地温度.

采用雷诺时均方法计算中，不能获得脉动速度的分量引起的熵产率，此时脉动速度产生的熵产率Spro,D′可根据FABIAN等[13]提出的方法来计算，公式为

(3)

式中：β=0.09；ω为湍流涡黏频率;ρ为流体密度；k为湍动能.

熵产率均存在较强的壁面效应，壁面附近熵产率计算公式[14]为

(4)

式中：τ为壁面剪切力；v为近壁面速度.

(5)

(6)

(7)

(8)

式中:V为计算域体积；A为计算域壁面面积.

2 研究模型与数值计算

2.1 研究模型

旋流泵设计的参数中，流量Q=60 m3/h，扬程H=16.0 m，转速n=2 900 r/min，叶片数Z=10.主要几何参数中，蜗壳进口直径为85 mm，蜗壳出口直径为80 mm，基圆直径为D3=160 mm，叶轮外径D2=128 mm，叶轮出口宽度b2=33 mm.运用Creo 6.0进行旋流泵叶轮、蜗壳、进出口延长段的水体造型，其中进出口延长段为直管结构，考虑到流体的不充分发展及流体回流会对计算精度造成影响，使泵体出口段长度和泵体进口段为5倍直径.各部分计算域模型如图1所示.

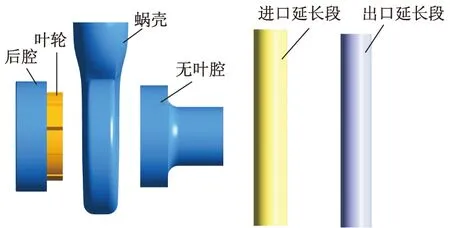
图1 流体计算域

2.2 数值计算

使用ICEM分别对旋流泵各计算流体域进行高质量结构化网格划分，计算域各部分网格质量均高于0.3.由于旋流泵蜗壳隔舌处曲率变化较大，因此对隔舌附近的网格进行局部加密，如图2所示.

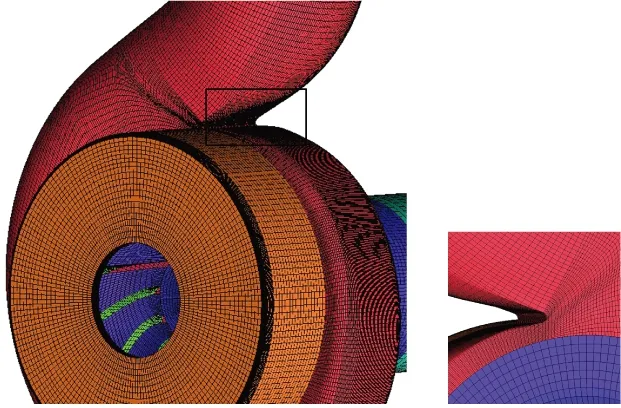
图2 局部网格示意图

通过6套不同密度的网格对网格无关性进行检查.不同网格数下的扬程曲线如图3所示.从图3中可知，当网格数量N低于200万时扬程变化幅度较大，高于200万时扬程预测值逐渐趋于稳定，网格数为200.54 万的方案与网格数为526.30万的方案扬程的变化误差在1%以内.为兼顾计算机的运算速度和计算效率，选取网格数为200.54万的方案为最终网格方案.

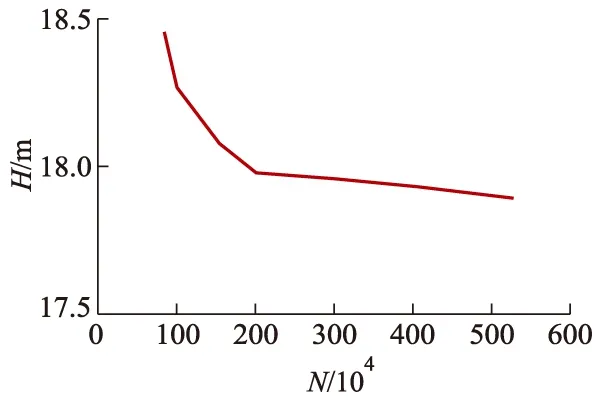
图3 网格无关性检查

流场计算采用商业软件Ansys CFX，湍流模型采用标准k-ε模型，边界条件采用进口压力和出口质量流量.

3 结果及分析

3.1 数值方法验证

图4为试验实测和数值模拟的旋流泵扬程和效率曲线.从图4中可以看出，试验与模拟的扬程、效率曲线变化趋势一致，吻合良好，各工况下数值计算和试验值相对误差均小于5%.这说明采用的CFD方法是基本可靠的.

图4 旋流泵外特性曲线

3.2 不同工况下旋流泵各部分的熵产分布特征

图5为不同流量下旋流泵各过流部件熵产值变化曲线，其中Stotal为旋流泵整体的总熵产值；Simp为叶轮区域的熵产值；Svol为蜗壳和后腔区域的熵产值；Sinlet为进口延长段区域的熵产值；Soutlet为出口延长段区域的熵产值.

从图5中可以看出，随着流量的增加，总熵产值先减小后增加，设计流量下的总熵产值最小，这表示随着流量的增加，旋流泵运行中的能量损失逐渐减小，超过设计流量后能量损失又逐渐增大.蜗壳及后腔区域的熵产值也呈现出先减小后增大的趋势，叶轮区域的熵产值随流量的增加一直呈增长趋势.进口延长段和出口延长段的总熵产值则表现为相反的变化趋势，随着流量的增加，进口延长段的熵产值逐渐减小，而出口延长段的熵产值有小幅度的增加.

图5 不同流量下各过流部件内的熵产

为更进一步探究不同流量下旋流泵内能量损失情况，分别对小流量、设计流量、大流量这3种工况下旋流泵各个过流部件的熵产值进行分析.从图6中可以看出，3种工况下无叶腔、后腔区域的熵产占总熵产的比例均超过了70%，是所有过流部件中能量损失最大的位置.小流量工况下进口延长段的熵产值占总熵产的比例最大为7.41%，设计流量、大流量工况下进口延长段的熵产占比下降至1%以下.出口延长段的熵产占比在3种工况下都相对较低，均在3%以下.叶轮区域的熵产占总熵产的比例和流量明显正相关，设计流量、大流量下占比超过20%.

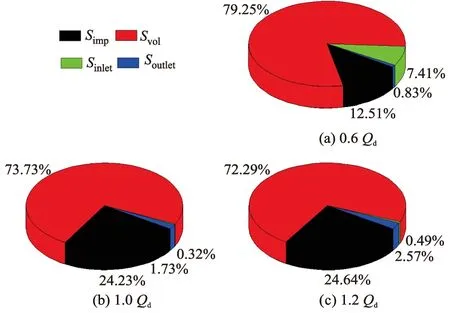
图6 不同流量下各过流部件的熵产占比

3.3 不同工况下旋流泵内整体流态特征

图7为旋流泵中间截面的流线和熵产S分布.从图7a中可以看出,随着流量的增大，无叶腔内的涡结构数量减少，泵内流线均匀性整体提高，叶轮内的流态逐渐恶化.从图7b中可以看到,随着流量的增大，无叶腔内熵产逐渐减小，叶轮区域熵产逐渐增大.在小流量工况下泵内总体熵产高于另外2个工况，泵体内涡结构数量多，且涡流间影响显著，涡结构的交界处熵产明显高于其他区域.

图7 不同工况下旋流泵中间截面的流线和熵产分布

3.4 不同工况下蜗壳内流态特征

为进一步细化分析各部分损失产生的原因，采用基于Q准则[15]的涡识别方法对流场中的涡结构进行识别.其定义式为

(9)

式中：Ωij为旋转张量；Sij为应变率张量；当Q>0时表示流体运动中旋转作用占主导.

图8为3种流量工况下，旋流泵泵腔内的涡核和熵产分布，其中涡核分布用流速染色.图8a显示，泵腔内的涡核主要分布在后腔、无叶腔以及隔舌处.后腔、无叶腔内的涡核大致呈带状分布，随着流量增加，涡核的分布更加集中，涡核尺寸有所减小.小流量工况下，后腔内涡核结构复杂、尺寸较大；无叶腔内涡带分布较为分散，有2条较窄的涡带；隔舌前端有面积较大的低速涡团.随着流量增大，设计流量下，后腔的涡核尺寸略有减小；无叶腔内涡带数量减少，集中为一条涡带；隔舌前端的流态趋于稳定，低速涡团消失仅存在一些小尺度的涡核.大流量工况下，后腔、无叶腔涡核分布变化不大，而蜗壳隔舌处由于动静干涉作用增强，隔舌前端涡核尺度又有所增长.

从图8b熵产分布图中可以看出，在不同工况下随着流量不断增大，后腔、无叶腔的高熵产的区域先减小后增大，而隔舌处的熵产随流量增大变化不大.在小流量工况下，后腔和无叶腔内都有明显的高熵产区域；在设计流量工况下，高熵产区域仅小范围集中于隔舌以及后腔处，这说明随着流量增大，泵体内的流态逐渐趋于稳定，泵体内的能量损失减小；在大流量工况下，无叶腔内的熵产有小幅增大，而后腔内由于流速增大和冲击增强导致熵产迅速增大.

图8 不同工况下泵腔内涡核和熵产分布

3.5 不同工况下叶轮内流态特征

图9为不同工况下叶轮内涡核、流线以及熵产分布.由图9a可知，无论是小流量工况还是设计流量工况下，旋流泵叶轮流道内都有涡核存在，并且随着流量的增大，涡核面积逐渐增大，设计流量、大流量工况时涡核几乎充满了整个流道.从图9b可以看出，随着流量增大，叶轮进口流速逐渐增大，叶轮流道内的流态逐渐紊乱，有大量旋涡产生，进而造成叶轮流道堵塞和回流.从图9c可以看出，随着流量增大，叶轮高熵产区域的范围逐渐增大；从熵产分布的位置看，叶轮流道内的熵产主要集中分布在流道入口处，流道出口也有小范围的高熵产区域.小流量工况下，叶轮只有个别流道进出口存在高熵产区域；设计流量工况下，叶轮进出口熵产迅速增大，所有流道都存在高熵产区域；大流量工况下，进出口的熵产进一步增大.设计流量工况和大流量工况下，叶轮进口熵产的增大是由于流道内大量的旋涡造成流道阻塞，流道入口的流速显著增大，水力撞击带来能量损失也随之增加；叶轮出口熵产增大是由于叶轮出口的旋涡脱落和回流造成的.

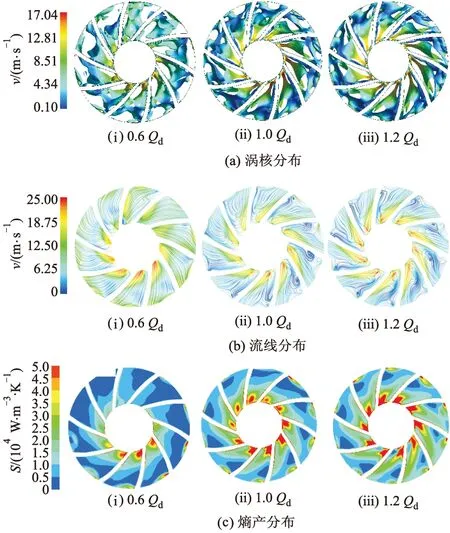
图9 不同工况下叶轮内涡核、流线以及熵产分布

3.6 不同工况下进口延长段内流态特征

图10为3种流量工况下旋流泵进口延长段的流线、熵产分布.从图10a可以看出，随着流量增大，进口延长段流态逐渐稳定.小流量工况下进口延长段内存在大量的涡团，流态十分紊乱；设计流量、大流量下流道内的涡团消失，整个流道内流体速度迹线分布均匀，流态较好.从图10b可以看出，随着流量增大，进口延长段的熵产逐渐减小.小流量工况下进口流道回流严重，造成了较大的能量损失，高熵产区域面积较大；随着流量的增大，进口流道的熵产值明显减小.

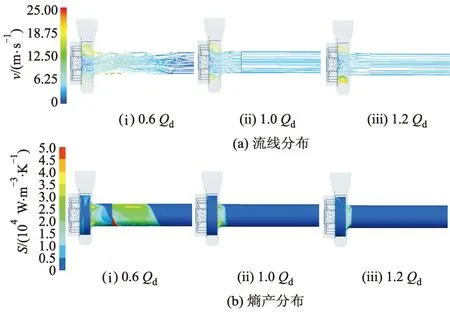
图10 不同工况下进口延长段流线分布和熵产分布

4 结 论

采用CFD方法结合熵产理论分析了旋流泵不同工况下的内流损失特性及其流动结构，研究得到如下结论：

1) 旋流泵运行过程中的总熵产随流量增大先减小后增大，其中熵产最大的区域是无叶腔及后腔部分，这部分的熵产占总熵产的70%以上.叶轮区域的熵产值随流量增大而增大，设计流量、大流量工况下叶轮区域的熵产占比超过20%.进口延长段区域的熵产随流量的增大而减小，设计流量、大流量工况时占比低于1%.出口延长段的熵产占比相对较低，所有工况均在3%以下.

2) 旋流泵在不同流量工况下运行时，流动不稳定发生的区域有所不同.小流量工况下，泵体无叶腔内的涡带有2条；隔舌前端有较大尺度的低速涡核；进口延长段有明显的大尺度涡团和回流现象.设计流量工况下，蜗壳无叶腔和进口延长段的流场趋于稳定，但叶轮流道的涡核尺寸增大，旋涡数量增多.大流量工况下，泵腔内的涡核尺寸变化不大，但流速增大；叶轮区域涡核尺寸继续增大，流场不稳定程度加剧.

3) 旋流泵运行过程中在蜗壳隔舌、后腔以及叶轮处的熵产相对较高，因此在进行旋流泵优化设计时，可以从蜗壳隔舌安放角、后腔与叶轮的适配以及叶轮形式等方面着手降低流动损失，以提高泵的工作效率和稳定性.