基于压实振动信号的路基压实度检测系统研究

摘要：路基施工是公路施工过程中的重要环节，但其施工质量受环境因素、施工设备及施工人员素养等众多因素的影响易出现质量风险，常规的事后检测方法不能满足对路基压实质量的连续、实时监测的要求。文章建立了压路机与路基之间的振动轮-路基动力学模型，分析了路基压实度与压路机振动信号的关系，提出了基于振动加速度信号的路基压实度快速實时检测方法，并验证了该方法的有效性。

关键词：道路工程;路基压实度;加速度信号;动力学模型;压实度检测系统

文献标识码：U416.06-A-11-029-5

0 引言

坚实可靠的路基是道路长期高品质运行的必要保证。现行规范及常规路基压实质量检测方法有灌砂法、环刀法、核子检测法等[1]。灌砂法操作过程可控，数值及检测结果准确，是工程实际中路基压实度检测的常用方法。环刀法是我国传统的压实度检测方法，是一种抽检的方法并且对检测人员专业素养依赖较大。核子检测法则是国际上广泛应用的压实度及含水量检测手段，但是其仪器具有放射性、操作步骤繁琐等缺点。总之，常规这些方法都是施工完成的事后检测，并且对路面破坏性大，检测过程繁琐，人为影响因素较多，不能有效保证路基施工的可靠性、及时性、经济性。

刘东海等研发了路基压实度实时监测装置，建立了以路基压实检测值为核心变量的路基压实质量评估模型，实现了施工面作业质量的快速评估[2]。重庆大学黄志福等以压路机振动轮处加速度为检测对象，建立了压路机-路基系统的动力学模型，分析了压路机垂直方向加速度与路基材料刚度、阻尼之间的关系，提出了路基压实度连续检测技术的设计方案[3]。与加速度传感器采集振动轮振动信号用于反馈路基压实度方法不同，谭忆秋等人用光栅传感器检测车辙板试件中，通过分析试件的应变响应和压实次数的关系，实现对路面压实的过程分析[4]。此外，路基压实度的实时监测不仅能及时保证工程质量，还能引用于某些早期建造公路进行二次施工前的快速合理评估工程量[5]。陈镇金等基于路基压实理论开发出了路基施工过程中的振动压实智能化检测系统，通过对现有压路机进行加装加速度传感器、温度传感器、车载电脑等实现了对压路机施工质量的实时检测，实现了对路基施工压实质量的有效管理[6]。居彩梅等利用压路及振动轮的加速度值与路基的材料的正相关关系，提出振荡压实度计测量系统框图[7]。鉴于此，本文通过建立振动轮-路基动力学模型[8]，分析研究振动加速度信号与压实度之间的关系，提出了基于加速度信号的路基压实度连续检测技术。

1 理论分析

1.1 振动轮-路基动力学模型

压路机在进行路基压实作业中，主要是利用振动轮的静载荷重量以及振动轮内偏心块的离心力产生的动载荷进行压实作业。其作业质量不仅取决于振动轮的工作条件、压路机结构参数及工况参数，还与路基材料及状态有关。而要通过安装在压路机上的振动传感器进行路基压实度的实时检测，就必须建立振动轮-路基动力学模型[9]，其中质量模型如图1所示。

压路机作业时机架和振动轮的运动可近似看作刚体移动和滚动，而路基随着施工次数的增多，其刚度和阻尼都会发生比较明显的变化。因此，将压路机机架当作集中质量m1，压路机振动轮主要在路基竖直方向进行路基的压实作业，则振动轮也可看作一个具有强迫振动源的集中质量m2，随振路基质量为m3;机架和振动轮之间的刚度及阻尼分别为k1及c1，而路基的刚度和阻尼分别为k2和c2;机架的位移为x1，振动轮竖直方向上的位移为x2，随振路基的位移为x3。假设振动轮与路基面之间始终接触，则x2=x3，ms=m2+m3。根据以上假设及参数建立压路机振动轮-路基动力学模型为式（1）：

m1x″1+c1（x′1-x′2）+k1（x1-x2）=0

m1x″2+c1（x′1-x′2）+k1（x1-x2）+Fs=F=F0sinωt（1）

m3x″3+c2x′3+k2x3-Fs=0

式中：F0=meω2——振动轮偏心块离心力;

e——偏心块的偏心距。

当偏心块以ω角速度转动时，激振力F0带动振动轮进入振动状态。则式写成矩阵形式为式（2）：

由式（2）～（7）可知，在压路机作业过程中，路基刚度k2和阻尼c2发生变化。因此，在偏心块激振力作用下，振动轮竖直方向上的加速度仅与路基参数有关。

1.2 振动轮加速度幅值及频谱分析

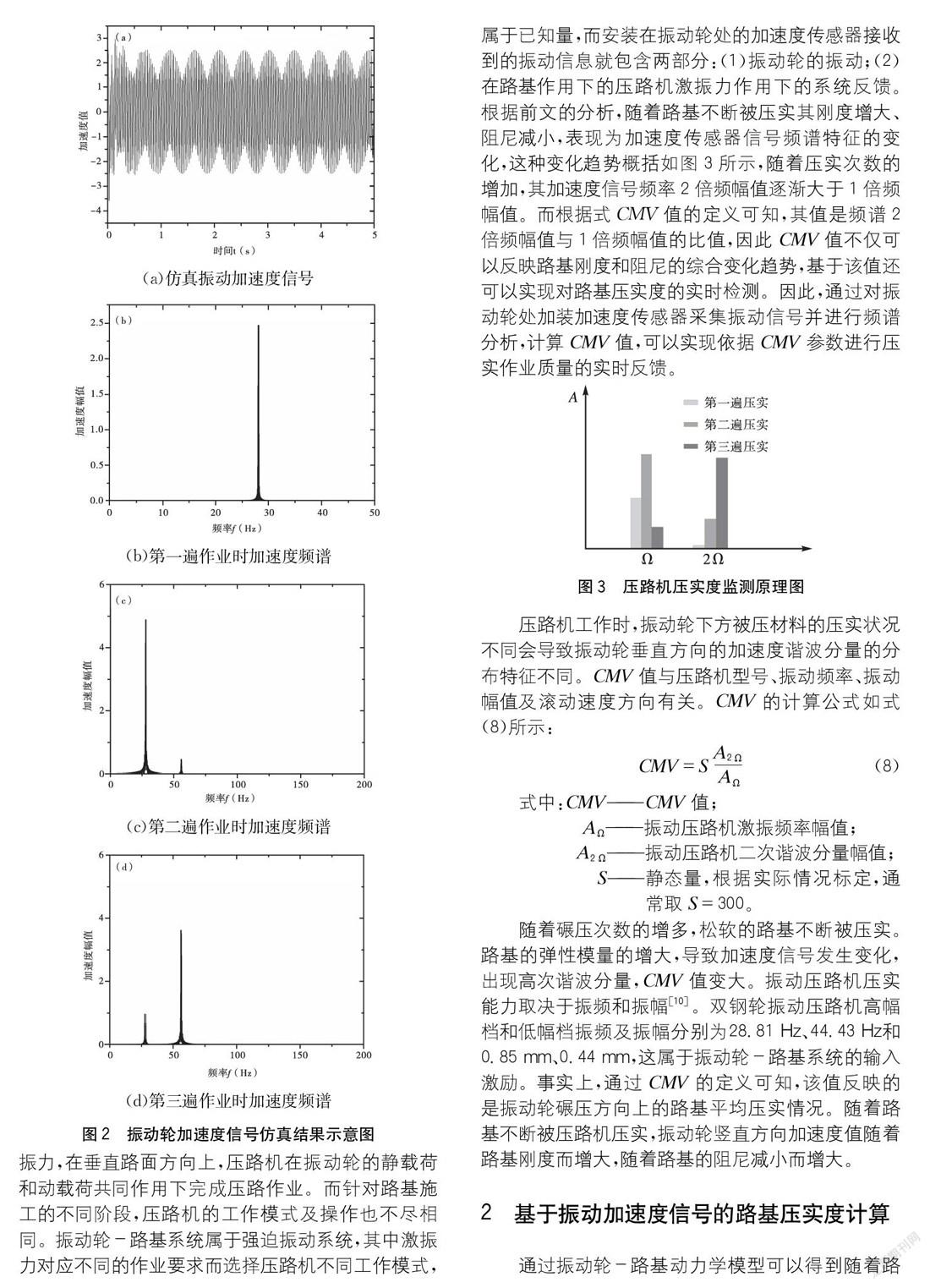
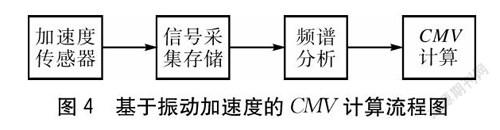
对振动轮-路基动力学模型进行求解，获得压路机振动轮的加速度值仿真数据。当压路机第一遍作业时，路基刚度较小、阻尼较大。加速度曲线表现出清晰的正弦曲线特性，而加速度信号频谱中以振动轮工频幅值为主，如图2（a）、图2（b）所示;而随着压路机第二遍作业时，路基的刚度加大、阻尼减小，加速度信号频谱中出现了工频二倍频幅值，如图2（c）所示;而当压路机第三次作业时，加速度信号频谱中二倍频谐波幅值大于工频幅值，如图2（d）所示，这是因为路基不断被压实后刚度明显增大，导致振动轮-路基系统动态响应中出现谐波成分。可知，加速度二倍频谐波成分的出现表示路基不断被压实。

1.3 CMV（Compaction Meter Value）压实度检测原理

压路机进行压实施工作业时，可将振动压路机-路基之间简化为三自由度非线性强迫振动模型。其中压路机振动轮内的偏心质量块所产生的离心力为激振力，在垂直路面方向上，压路机在振动轮的静载荷和动载荷共同作用下完成压路作业。而针对路基施工的不同阶段，压路机的工作模式及操作也不尽相同。振动轮-路基系统属于强迫振动系统，其中激振力对应不同的作业要求而选择压路机不同工作模式，属于已知量，而安装在振动轮处的加速度传感器接收到的振动信息就包含两部分：（1）振动轮的振动;（2）在路基作用下的压路机激振力作用下的系统反馈。根据前文的分析，随着路基不断被压实其刚度增大、阻尼减小，表现为加速度传感器信号频谱特征的变化，这种变化趋势概括如图3所示，随着压实次数的增加，其加速度信号频率2倍频幅值逐渐大于1倍频幅值。而根据式CMV值的定义可知，其值是频谱2倍频幅值与1倍频幅值的比值，因此CMV值不仅可以反映路基刚度和阻尼的综合变化趋势，基于该值还可以实现对路基压实度的实时检测。因此，通过对振动轮处加装加速度传感器采集振动信号并进行频谱分析，计算CMV值，可以实现依据CMV参数进行压实作业质量的实时反馈。

压路机工作时，振动轮下方被压材料的压实状况不同会导致振动轮垂直方向的加速度谐波分量的分布特征不同。CMV值与压路机型号、振动频率、振动幅值及滚动速度方向有关。CMV的计算公式如式（8）所示：

CMV=SA2ΩAΩ（8）

式中：CMV——CMV值;

AΩ——振动压路机激振频率幅值;

A2Ω——振動压路机二次谐波分量幅值;

S——静态量，根据实际情况标定，通常取S=300。

随着碾压次数的增多，松软的路基不断被压实。路基的弹性模量的增大，导致加速度信号发生变化，出现高次谐波分量，CMV值变大。振动压路机压实能力取决于振频和振幅[10]。双钢轮振动压路机高幅档和低幅档振频及振幅分别为28.81 Hz、44.43 Hz和0.85 mm、0.44 mm，这属于振动轮-路基系统的输入激励。事实上，通过CMV的定义可知，该值反映的是振动轮碾压方向上的路基平均压实情况。随着路基不断被压路机压实，振动轮竖直方向加速度值随着路基刚度而增大，随着路基的阻尼减小而增大。

2 基于振动加速度信号的路基压实度计算

通过振动轮-路基动力学模型可以得到随着路基不断被压实，其刚度不断增大而阻尼不断减小，路基的这种变化引起振动轮加速度幅值增大，在加速度信号的频谱中变现为出现振动轮频率二倍频的高次谐波。通过仿真分析以及路基压实度CMV的定义可以看到利用振动轮处的加速度信号测量及计算路基的压实度是可行的，其技术实现步骤如图4所示，主要是信号处理手段计算出CMV值，用于路基压实度反馈。

2.1 CMV与作业次数的关系

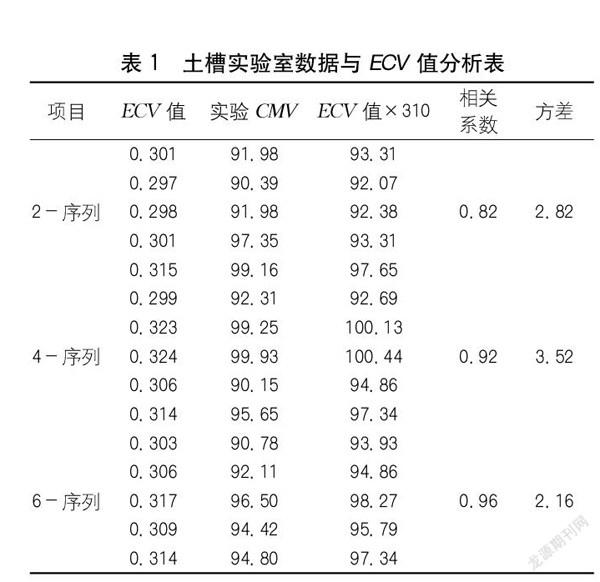
CMV可以反映路基被压实过程中路基刚度变化情况，但要将其应用于工程实际中，还应将其与路基密实度（ECV）进行对比。为此，多次进行土槽实验及场地测试，积累了大量的实验数据。作业现场记录的压实度曲线如图5所示，每遍压实的CMV值都有波动，特别是第三遍压实后CMV值出现较大和较小值。忽略异常离群点的影响，可以看出随着压实次数的增加，压实度呈现递增的趋势。

2.2 ECV值与实验数据的对比

为了分析CMV值与路基压实作业质量之间的关系，分别对土槽实验进行密实度ECV值及压实度CMV测量，得到结果如表1所示。ECV值与CMV成正相关趋势，相关系数最大达0.96，表明CMV与ECV值高度相关，并且实验数据的方差不大，最大方差3.52出现在第4组实验中，经过数据分析得到CMV与ECV之间的经验常数为310。

3 路基压实质量管理系统研究

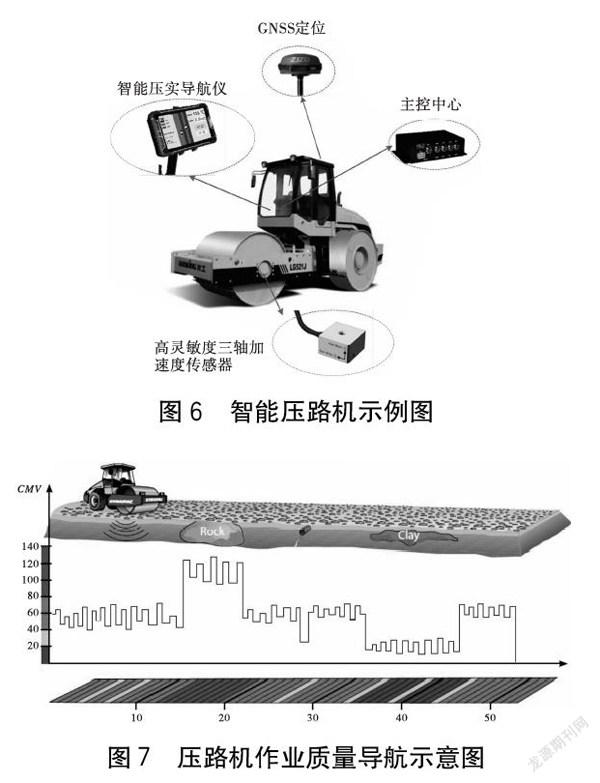
从CMV与路基参数之间的仿真及实验数据分析可知，CMV可以有效反馈路基在被压实过程中的参数变化，路基密实度越高，其CMV值越大。根据这一原理以及采集加速度信号的便利及经济性，在压

路机振动轮车架处安装三轴加速度传感器，并通过信号采集、信号分析及CMV值可视化等手段，研发出了路基压实质量管理系统，如图6所示。加速度信号以及GNSS定位系统将压路机当前振动信号及位置信息输送到主控中心进行计算后得到路基压实度CMV，将该值可视化后显示在驾驶室内的导航仪上，供施工作业人员参考;同时路基参数也会通过网络传送至数据中心及管理者办公室，方便项目内相关人员跟进项目进度和质量，提高管理效率。CMV可视化原理如图7所示。根据实时测量出的CMV值反馈路基压实质量，通过颜色进行区分，便于作业及管理人员进行有效监管。

路基压实质量管理系统不仅能在作业中对路基压实质量进行评价和测量，而且及时保证了公路路基施工质量，防止了偷工减料的发生。此外，所有施工数据永久保存，便于后期路基维护、项目评审、工程审核时使用，管理人员能实时掌握施工情况，避免浪费人力物力。

4 结语

本文通过建立压路机振动轮-路基之间的动力学模型，验证了CMV与路基压实质量之间的正相关关系，并通过试验方法计算了CMV与路基密实度之间的关系。通过对压路机进行加装传感器、作业质量导航及定位系统，完成了路基压实质量管理系统。主要结论如下：

（1）压实度连续检测方法科学可行，便于反映路基的压实情况。当压路机工作在松软路基上时，路基的阻尼较大，对于振动轮的能量吸收较多，CMV值较小;而当路基密实度增加，CMV值也变大，反映路基被压实。

（2）通过系统仿真和试验数据分析，计算比较了CMV值与路基密实度之间的相关关系，通过后期大量工程数据分析拟合出回归公式和系数，用于工程实践中。

（3）路基压实质量管理系统可实现对路基压实度的实时、连续检测，准确地反映路基压实度，有效控制路基施工质量，提高压实效率及质量，在公路路基施工中有广阔的应用前景。

参考文献

[1]苏冬兰.公路路基压实度影响因素及检测技术对比分析[J].福建建材，2020，8（8）：17-19.

[2]刘东海，巩树涛，魏宏云.基于实时监测的高等级公路路基压实质量快速评估[J].土木工程学报，2014（47）：138-144.

[3]黄志福，梁乃兴，赵 毅，等.路面压实度自动连续检测技术[J].长安大学学报（自然科学版），2015（35）：24-32.

[4]谭忆秋，王海朋，马韶军，等.基于光纤光栅传感技术的沥青路面压实监测[J].中国公路学报，2014（27）：112-117.

[5]Zhang J-H，Ding L，Zheng J-L，et al.Deterioration mechanism and rapid detection of performances of an existing subgrade in southern China[J].Journal of Central South University，2020，27（7）：2 134-2 147.

[6]陈镇金.路基施工振动压实智能化检测系统及应用研究[D].长沙：长沙理工大学，2017.

[7]居彩梅.车载式压实度检测仪[D].西安：长安大学，2001.

[8]Wang J，Sha A，Hu L.Modelling vibratory roller–soil system dynamics using discrete element method[J].International Journal for Engineering Modelling，2018，31（3）：35-50.

[9]易 飞.振动压路机振动加速度实时检测及数据处理研究[D].重庆：重庆交通大学，2011.

[10]王子芳，曾晓江.公路路基路面压实施工技术应用[J].交通世界，2020（552）：87-88.

收稿日期：2021-03-18

作者简介：

任少博（1985—），硕士，工程师，主要从事道路结构力学计算、技术咨询以及智慧工地建设方面的研究工作。