基-面层局部黏结失效对半刚性基层沥青路面拉裂破坏的影响分析

包聪灵 许新权 谢光宁 蔡正森 肖 瑶

(广东华路交通科技有限公司 广州 510420)

0 引 言

弹性层状理论体系作为我国沥青路面结构设计和计算的理论支撑，具有其独有的优点[1-2].该理论认为沥青路面各层材料为各向同性的弹性体且各层之间完全连续[3-4]，但是在摊铺现场，过渡层局部施工均匀性欠佳、污染、磨损现象会使得层间连续接触的状态发生破坏，会使得沥青路面受力状态局部发生突变，导致沥青路面产生拉裂破坏.彭红卫等[5]调查和统计了湖南省高速公路沥青路面裂缝病害并对其产生原因进行分析，认为层间接触不完全连续是半刚性基层沥青路面产生拉裂破坏的重要原因之一，但是局部层间黏结具体会对拉裂破坏有哪些影响并未给出明确结论.杨庆国等[6-7]认为沥青路面面层和基层间的黏结状态的变化都是从小区域出发然后逐渐扩展，最终演变成早期病害.但是，对于究竟多大的黏结失效区域面积会对沥青路面拉裂破坏产生显著影响并没有明确的论断.

大多数学者以弹性模型进行沥青路面的计算和研究，少有基于弹塑性理论的分析[8-9].但是把沥青路面材料视为弹性体与实际情况存在偏差，沥青作为柔性材料，在荷载的作用下会产生弹性变形、黏弹性变形及塑性变形，弹性变形在撤销作用荷载后会恢复，而塑性变形会在荷载的反复作用下进行积累，因此对于沥青路面以弹塑性进行力学分析是很有必要的，而且还需考虑重载、超载对沥青路面的破坏[10].

沥青路面拉裂破坏主要跟竖向变形和沥青面层层底拉应变相关.文中采用弹塑性理论，建立考虑重载作用的三维弹塑性有限元模型，利用有限元的方法分析了基、面层局部黏结失效区域大小和黏结强度的对沥青路面拉裂破坏的影响.

1 力学计算模型

1.1 路面结构及参数

采用典型半刚性基层沥青路面结构形式.上、中面层采用SBS改性沥青混合料规格分别为AC-13和AC-20；下面层为基质沥青混合料规格为AC-25；基层和底基层为水稳碎石；垫层为级配碎石.为了研究沥青混凝土层的塑性变形能力，所有沥青层采用弹塑性本构模型，其他各层采用弹性本构模型.路面结构的弹性参数依据相关设计图纸和规范取值，塑性参数参照邱阳阳等[11]的研究成果，具体数值见表1.

表1 路面结构参数

1.2 模型尺寸和单元选择

为了模拟路面的受力情况，需要尽可能的增加模型的尺寸使之逼近实际路面的尺寸，但是模型尺寸过大则会增大计算的工作量，因此总结以往的研究经验，本文取模型尺寸为6 m×6 m×6 m.分别采用八节点六面体单元和20节点六面体单元进行计算，结果表明：改变单元类型对力学结果影响很小，但是20节点六面体单元与八节点六面体单元相比，计算时间大幅增加，因此，本文取八节点六面体进行计算.

1.3 网格划分和边界条件

为提高计算的精度，在Y向(竖向)上，面层网格取0.005 m，水稳层网格取0.02 m，垫层取0.04 m，土基取0.1 m；在X向(道路横向)荷载作用区域的3倍宽带范围内取0.005 m，其他区域取0.05 m；在Z向(行车方向)荷载作用区域的3倍宽带范围内取0.005 m，其他区域取0.05 m.

根据沥青路面的受力特点，土基底面完全固定，左右两面约束X向(道路横向)的位移，前后两面约束Z向(行车方向)位移.

1.4 荷载及分析工况

文中考虑重载的作用，取车轮荷载分别为100，200，300 kN，分析不同黏结失效区域大小力学响应的影响.在此基础上，考虑局部黏结状态对各指标的影响，见图1.

图1 模型及荷载示意图

为了简化计算模型、提高计算的精度，本文荷载作用的区域和黏结失效区域均为矩形.为了分析黏结失效区域大小对力学响应的影响，取黏结失效区域的大小分别为完全黏结(面积为0 m2)、10 cm×10 cm、20 cm×20 cm、40 cm×40 cm和60 cm×60 cm.

为了表征黏结失效区域的黏结强度，引入ABAQUS容许“弹性滑动”的罚磨擦的定义，见图2.“弹性滑动”是在黏结的接触面之间发生的小量相对移动，ABAQUS会自动选择罚刚度(虚线的斜率)，并且这个“弹性滑动”是单元特征的很小一部分.

图2 ABAQUS中“罚”摩擦公式的定义

文中将基层和面层之间的法向磨擦定义为“硬接触”，即接触面之间能够传递的接触压力的大小不受限制，当接触压力变为负值或0时，两个接触面发生分离，并且相应结点上的约束会失效.局部失效的切向摩擦定义为“罚”，其他区域的接触定义为绑定即接触面在整个分析过程中都是始终紧密接触的，相当于将两个部分定义为一个整体[12].

根据彭妙娟等[13]研究结果发现：在摩擦系数在0.1～1.5之间时对力学响应的影响较大，当大于1.5时，基面层影响黏结强度对力学响应的影响极小，相当于完全黏结，因此本文为表征黏结失效区域的黏结强度，取摩擦系数分别为0、0.1、0.5、0.8、1.0和1.5.

2 对竖向变形引起的拉裂破坏的影响

竖向变形是引起沥青路面拉裂破坏的间接原因.当基、面层完全黏结时，路面结构受力对称，竖向变形在道路横向上呈对称分布，当基、面层局部黏结失效时，竖向变形不再对称分布，存在竖向变形差，此时路面受力不再平衡，不平衡的受力会使得沥青路面产生拉裂破坏.黏结失效区域选在单个车轮的底部，因此在路表取道路横向过车轮中心的路径，研究不同基、面层层间局部黏结状态对竖向变形的影响.

2.1 黏结失效区域大小的影响

考虑重载的作用，因此取荷载为200 kN，层间黏结状态取完全失效，分析黏结失效区域大小对竖向变形引起沥青路面拉裂破坏的影响.最大竖向变形值和两车轮荷载中心竖向变形的差值见表2.

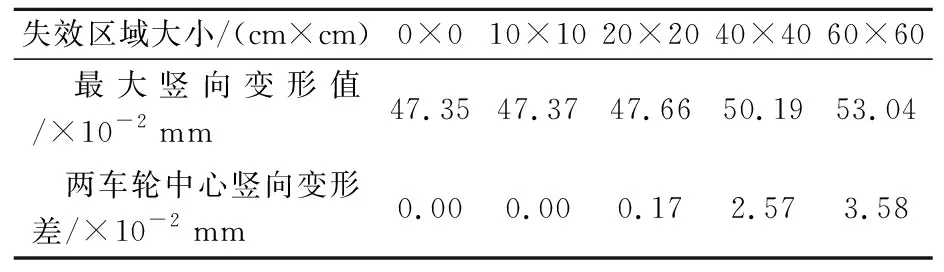
表2 黏结失效区域大小对竖向变形最大值及车轮中心竖向变形差值的影响

由表2可知：随着基、面黏结失效区域面积的增大，最大竖向变形值和两车轮中心竖向变形差均逐渐增大；当由完全黏结逐渐扩展到60 cm×60 cm时，竖向变形最大值增加12%，两车轮中心竖向变形差增加3.58×10-2mm，增加程度相对较小.

为了进一步研究黏结失效区域大小对最大竖向变形的影响，将区域大小换算成面积，并绘制最大竖向变形随面积大小的变化规律图，见图3.

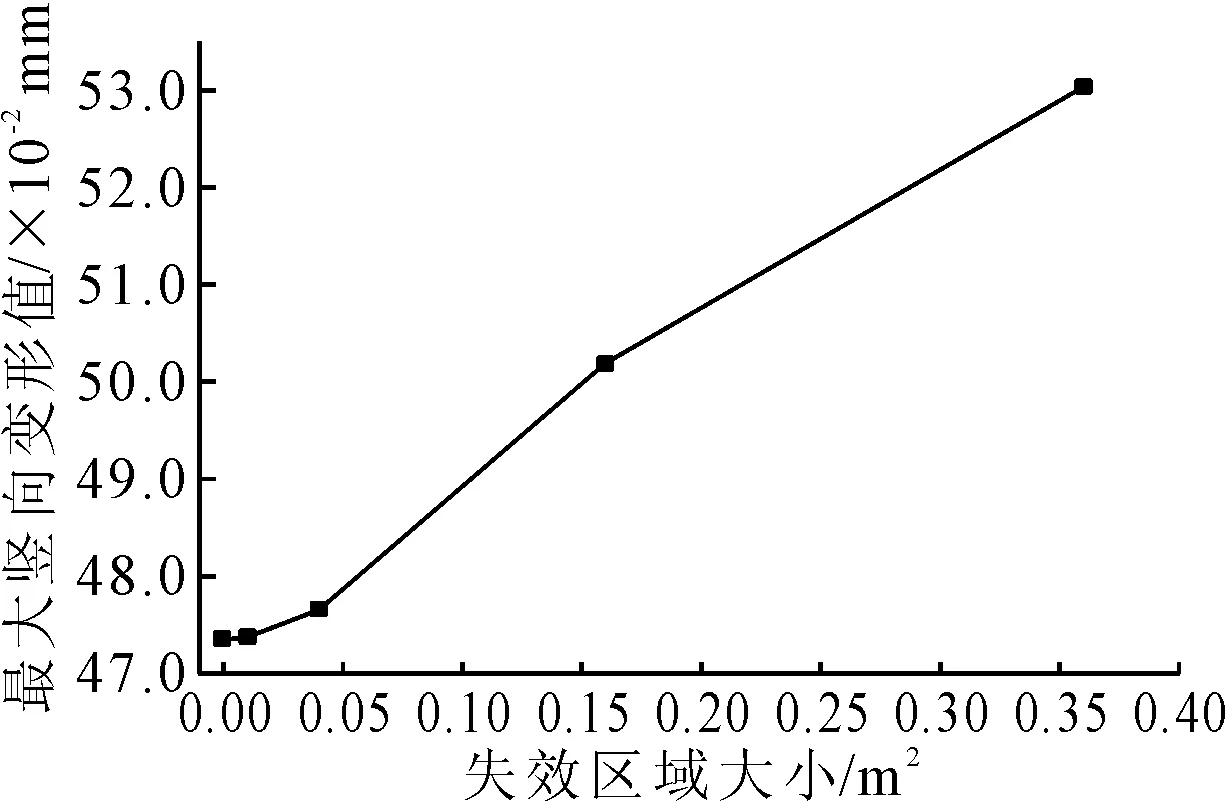
图3 最大竖向变形值随黏结失效区域面积的变化

由图3可知，最大竖向变形值随基-面层局部黏结失效区域的面积近似呈“S形”分布，当黏结失效区域面积小于等于0.04 m2时，面积大小对竖向变形的影响较小，虽然经过线性拟合后增长率达8.192 3，但是整体数值变化不大；当面积大于0.04 m2时，失效面积对竖向变形的影响增大，通过线性拟合可知其增长率高达16.551 0.说明基、面层黏结失效区域在小于0.04 m2时可以忽略其对竖向变形的影响，而当黏结失效区域面积大于0.04 m2时应引起重视，此时路面产生数值差别极大的不平衡的竖向位移，在荷载的反复作用下，不平衡位置极有可能产生拉裂破坏.

2.2 荷载大小的影响

为了说明荷载大小对最大竖向变形的影响，固定局部黏结失效区域为60 cm×60 cm，层间黏结完全失效，分析不同轴重对竖向变形的影响，结果见表3.

表3 轴重对竖向变形最大值及车轮中心竖向变形差值的影响

由表3可知：随着轴重的增大，最大竖向变形值和两车轮中心竖向变形差均逐渐增大；当轴重为200 kN时，竖向变形最大值和两车轮中心竖向变形差值与100 kN相比分别增加70%和418%；当轴重为300 kN时，竖向变形最大值和两车轮中心竖向变形差与100 kN相比分别增加151%和881%，说明随着轴重的增加由竖向变形引起的拉裂破坏程度增大，破坏效果更加明显.

2.3 黏结强度的影响

为了单独分析黏结失效区的黏结强度对竖向变形的影响，固定轴重为标准轴重100 kN，局部黏结失效区域为60 cm×60 cm，竖向变形最大值和两车轮荷载中心的竖向变形差值随失效区域间黏结强度(摩擦系数)的变化规律见表4.

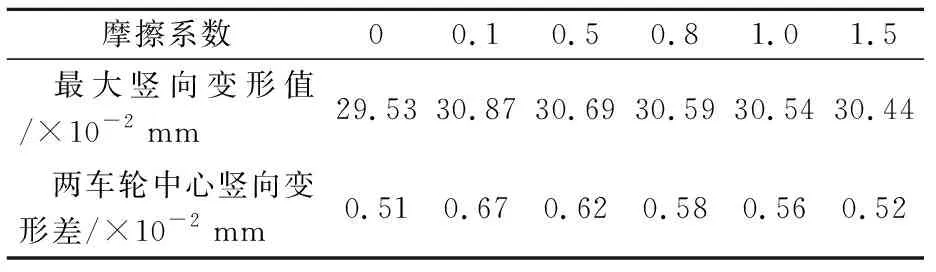
表4 黏结强度对竖向变形最大值及车轮中心竖向变形差值的影响

由表4可知，随着摩擦系数的增加，最大竖向变形值逐渐减小，且逼近与完全黏结时的状态，说明在一般计算时，不能简单的将基面层考虑为完全滑动或完全黏结状态.这也从侧面反映出基、面层层间黏结效果对沥青路面早期破坏具有较大的影响.随着基面层黏结强度的增加，两车轮中心竖向变形差逐渐减小，且整体而言差值较小，可忽略不计，说明摩擦系数对竖向变形引起的拉裂破坏几乎不存在影响.

3 对面层底拉应变引起的拉裂破坏的影响

沥青各层底拉应变作为引起沥青路面拉裂破坏的直接原因.考虑重载的作用，取轴重为200 kN，对模型进行加载，根据以往研究结果，沿行车方向的拉应变总是大于道路横向上的拉应变.因此，本节取沥青层层底行车方向的拉应变进行分析，总应拉变LE33在面层中的分布云图见图4.

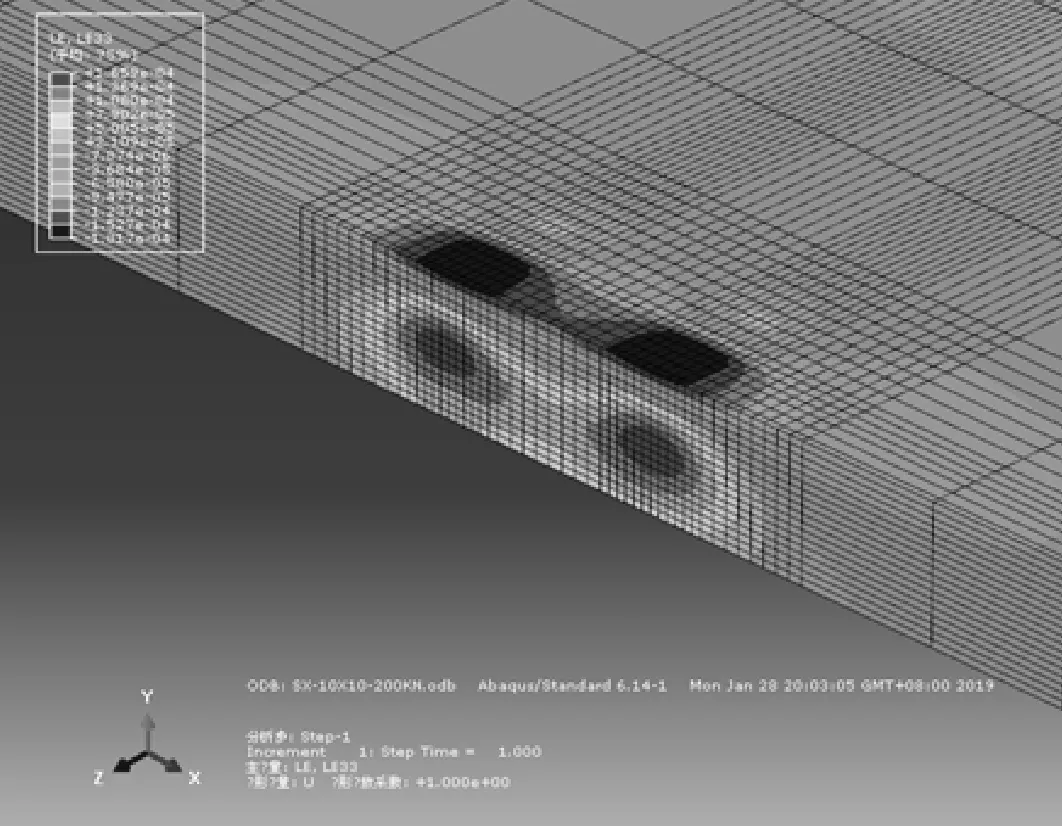
图4 总应变在沥青面层中的分布云图

由图4可知：总应变在车轮荷载作用中心的位置取得最大值，因此，在脱空区域的一侧，选过车轮荷载中心沿深度方向上的路径分析不同基、面层层间局部黏结状态对层底拉应变的的影响.

3.1 黏结失效区域大小对拉裂破坏的影响

考虑重载的作用，取荷载200 kN，分析黏结失效区域大小对拉应变的影响.总拉应变、弹性拉应变和塑性拉应变在黏结失效区一侧车轮荷载中心沿深度方向的路径上随失效区域大小的变化见图5.

由图5a)可知，在上面层中，总应变主要是压应变，且最大值在路表取得；在中、下面层中，总应变主要是拉应变；并且当黏结失效区域大于0.04 m2时，总拉应变最大值在中面层底取得，当大于0.04 m2时，总拉应变最大值在下面层底取得.

图5 三种应变在荷载作用中心沿深度方向的总拉应变分布图

由图5b)可知，考虑不同的黏结失效区域大小，弹性应变的变化规律基本相同.上面层主要是压应变，中、下面层主要是拉应变.当黏结失效区域面积大于0.04 m2时，上面层顶压应变随着黏着失效区域的变化较为显著；黏结失效区域大小为0.36 m2时的压应变最大值为无黏结失效区域的1.49倍，为0.16 m2的1.16倍，说明黏结失效区域面积在逐渐扩展到大于0.04 m2时，对沥青路面压密变形影响极为显著.

由图5c)可知：上面层中塑性应变为0，塑性拉应变主要产在中、下面层中产生.当黏结失效区域面积小于0.04 m2时，塑性拉应变的最大值在中面层底取得，此时面层的拉伸破坏主要是在中面层产生；当黏结失效区域面积大于0.04 m2时，塑性应变的最大值在下面层底取得，且随着黏结失效区域面积的增大，塑性拉应变显著增大，当黏结失效区域为0.36 m2时，塑性应变最大值为481.35×10-6是0.04 m2的1.50倍，是0.01 m2的4.40倍.说明当黏结失效区域面积大于等于0.04 m2时，在车辆荷载的作用下，路面的拉裂破坏首先是在下面层产生，随着荷载的不断作用，塑性拉应变反复产生积累，黏结失效区域面积逐渐扩大，并且向上发展，最终导致路面出现坑槽和U形滑移，因此，在路面结构设计时要适当提高下面层的抗疲劳性能.

3.2 荷载大小拉裂破坏的影响

由3.1可知，黏结失效区域大小为60 cm×60 cm时对拉应变的影响最大.因此本节固定局部黏结失效区域为60 cm×60 cm，分析不同轴重对拉应变影响.不同轴重作用下路面各层层底总拉应变最大值和塑性拉应变最大值见表5～6.

表5 轴重对面层各层层底总应变最大值的影响

由表5可知：沥青路面各层层底总应变均为拉应变，且随着轴重的增大，各层层底拉应变逐渐增大.说明当存在黏结失效区域时轴重对下面层总拉应变的影响最为显著，其次是上面层，对中面层的影响最小.但是由于现在路面结构设计过程中，上面层作为磨耗层，一般都采用改性沥青和力学性能较好的集料，对下面层一般采用普通沥青，集料的力学性能也相对较差，因此当存在局部黏结失效时，由面层引起的拉裂破坏首先是在下面层产生，然后慢慢向上传递形成坑槽.

由表6可知：沥青路面各层层底均产生的受拉的塑性应变，且上面层中产生的应变最小，下面层产生的应变最大.塑性应变的叠加是引起沥青路面拉裂破坏和黏结失效区域扩展的主要原因，说明随着轴重的增大，下面层最先产生拉裂破坏，且对轴重的敏感性最强.

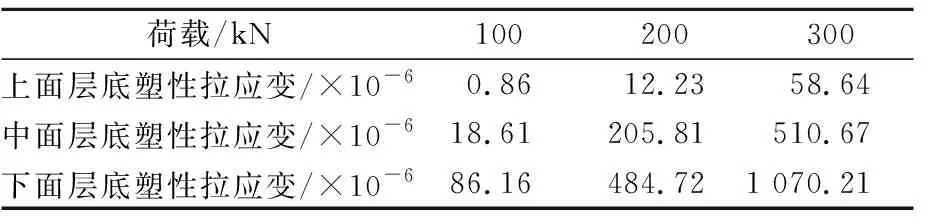
表6 轴重对面层各层层底塑性应变最大值的影响

3.3 黏结强度对拉裂破坏的影响

为了单独分析黏结失效区的黏结强度对拉应变的影响，固定轴重为标准轴重100 kN，局部黏结失效区域为60 cm×60 cm，沥青下面层层底总拉应变、弹性拉应变和塑性拉应变随层间黏结强度(摩擦系数)的变化规律见图6.

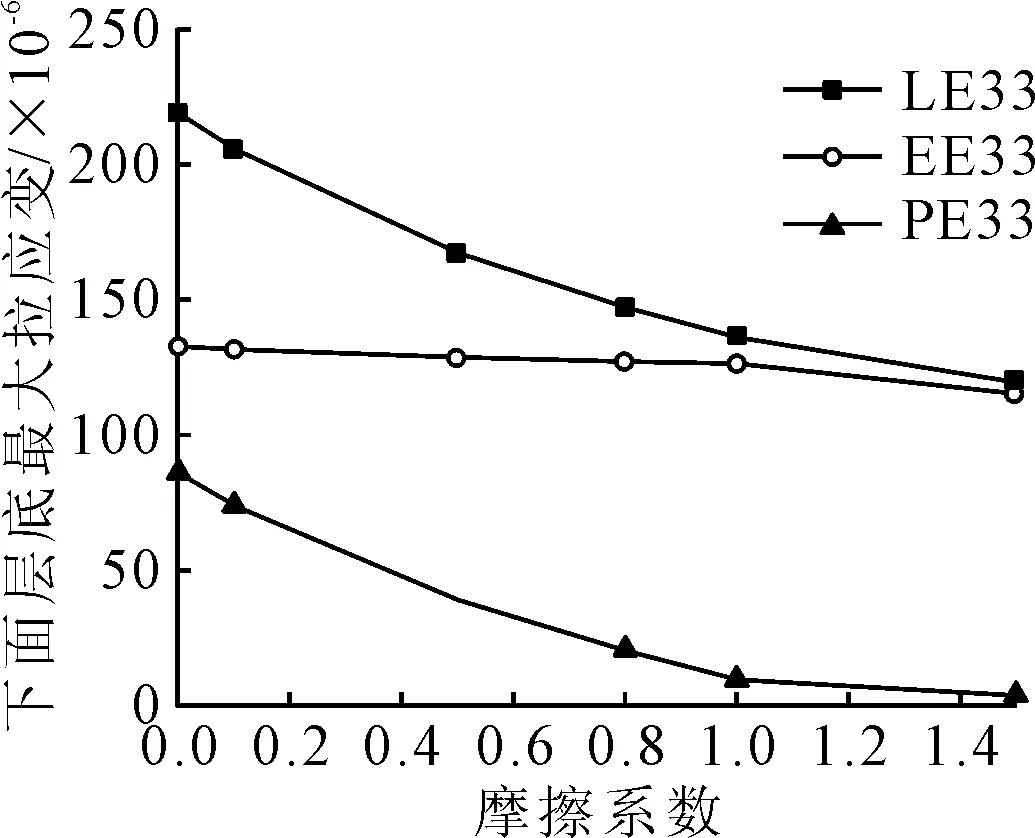
图6 下面层底总应变最大值随摩擦系数的分布图

由图6可知：随着基、面层黏结强度的增加，弹性应变基本保持不变，总应变的变化规律和塑性应变的基本相同.随着摩擦系数的增大，塑性应变占总应变的比例逐渐减小，当摩擦系数大于1.0时，塑性应变接近于0，此时总应变主要由弹性应变组成.说明黏结强度对塑性应变引起的沥青路面的拉裂破坏极为重要，不应单纯的将基面层之间的黏结关系定义为完全黏结和完全光滑这两种简单状态.此外，也从侧面反映出以弹性模型进行路面力学响应计算时存在较大的误差.

4 结 论

1) 当黏结失效区域面积小于0.04 m2时，黏结失效对竖向位移和车轮荷载中心位移差影响较小，可忽略不计；当黏结失效区域面积大于0.04 m2时，随着荷载的增加，竖向变形最大值和两车轮荷载中心竖向变形差值都逐渐增大，此时由竖向变形引起的拉裂破坏也逐渐突出.

2) 拉应变主要在中、下面层产生，随着黏结失效区域面积的增大，面层各层底拉应变最大值由中面层逐渐向下面层转移，即破坏由中面层向下面层逐渐迁徙，总应变中塑性应变所占的比重也随之增大.

3) 存在黏结失效区域时轴重对下面层总拉应变的影响最为显著，其次是上面层，对中面层的影响最小.但是由于现在路面结构设计过程中，上面层作为磨耗层，一般都采用改性沥青和力学性能较好的集料，对下面层一般采用普通沥青，集料的力学性能也相对较差，因此当存在局部脱空时，由面层引起的拉裂破坏首先是在下面层产生，然后慢慢向上传递形成坑槽.

4) 不同轴重作用下，路面各层层底均产生的受拉的塑性应变，且上面层中产生的应变最小，下面层产生的应变最大，塑性应变的叠加是引起沥青路面拉裂破坏和黏结失效区域扩展的主要原因，说明随着轴重的增大，下面层最先产生拉裂破坏，且对轴重的敏感性最强.

5) 局部黏结失效区域的强度对下面层层底拉应变的影响极为显著，随着强度增加，塑性应变所占总应变的比例逐渐减小，换言之，当基面层完全黏结时，下面层底不产生拉裂破坏.