浅谈圣维南原理的启发式教学和课程思政方法

陈玉骥 鲁志雄 陈舟

摘    要：圣维南原理是“弹性力学”课程的一个十分重要的内容，在处理次要边界条件时具有重要的作用。文章根据作者多年的“弹性力学”教学体会，从圣维南原理的提出方法、圣维南原理概念中要注意的问题、圣维南原理的案例解析等三个方面探讨了圣维南原理的教学方法，同时对该知识点的课程思政进行了教学总结，以期对指导青年教师教学起到一定的帮助作用。

关键词：“弹性力学”;圣维南原理;启发式教学;课程思政

中图分类号：G642      文献标识码：A      文章编号：1002-4107（2021）12-0023-02

圣维南原理是“弹性力学”课程教学中的一个重点和难点[1]，该原理在弹性力学计算中应用较广。但其概念较为抽象，青年教师在教学中一般难以讲透，学生在学习中也感觉理解较为困难。作者从事了多年的“弹性力学”课程教学，下面主要从三个方面谈一下作者在该原理教学中的体会，并探讨了其课程思政的教学实践[2]，以供同行参考。

一、圣维南原理的提出方法

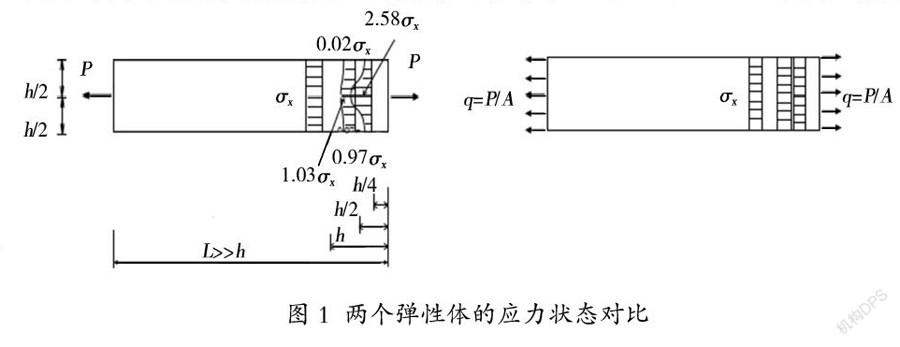
为了使学生对圣维南原理有一定的感性认识和加深学生对圣维南原理的理解，教师在教学中首先讲两个弹性体的应力状态对比分析的示例，由此提出圣维南原理。图1所示两个弹性体的几何形状和尺寸完全相同，仅面力不同（图1中，q=σx=P/A，A为杆件的截面积），但两者面力的合力相等，通过有限元计算得到靠端部h/4、h/2和h三个截面的正应力分布。由该图可见，两者的应力分布仅两端附近不同，在中间大部分范围，两者的应力状态完全相同。通过这一例子，可给出圣维南原理的第一种提法：“若将作用于弹性体一小部分边界上的一组面力用另外一组静力等效的面力代替时，则在该等效变换面力附近的应力状态将发生显著改变，而其他地方的应力状态基本保持不变。”然后，在圣维南原理第一种提法的基础上，通过分析比较图2所示三个弹性体的应力状态，可给出圣维南原理的第二种提法：“若作用于弹性体一小部分边界上的一组面力是平衡力系，则平衡力系附近的应力不为0，而其他地方的应力则基本为0。”

二、圣维南原理概念提出中要注意的问题

圣维南原理的两种提法中均要求满足两个条件。

（1）小部分边界即荷载（面力）作用边界范围在整个弹性体边界中占比很小。

（2）荷载（面力）必须为等效变换（第一种提法）或为平衡力系（第二种提法）。

这两个条件是应用圣维南原理的必要条件，两者缺一不可。如图3所示的两个弹性体满足上述两个条件，故可应用圣维南原理进行分析。但对于图3（b）所示弹性体，因为荷载作用的水平边界为大边界，故有些学生通常无法判断是否可应用圣维南原理。为此，在教学上要特别强调虽然该弹性体上的平衡力系是作用在大边界上，但该平衡力系所作用的边界范围在整个边界上仍然只占很小一部分，故仍然符合上述的第一个条件，因而也可应用圣维南原理。

三、圣维南原理的案例解析

弹性力学理论大都比较抽象、难懂，故在其知识点的讲授中，结合一些生活案例或结构案例予以应用分析，往往可以加深学生的理解和认识，也可提高学生学习的积极性，激发学生的学习热情。为此，作者在圣维南原理的教学中，采用了以下办法。

1.讲完圣维南原理的概念后，在课堂上叫一名学生起来，让他用一只手的两个手指头掐另外一只手的任一手指，然后问：“何处有痛感？头痛吗？脚痛吗？背痛吗？”（显然只有被掐处有痛感，其他地方则无痛感）。在学生进行回答后再做解释。该例子中，一只手的两个指头掐另外一只手的任一手指，从力学上看，相当于被掐手指上作用了一对大小相等、方向相反的集中力，之所以在被掐处有痛感，是因为该处应力很大;其他地方无痛感，是因为这些地方应力很小。该例子可使学生亲自体会圣维南原理，起到活跃课堂气氛、提高学生对圣维南原理的学习兴趣的作用。用老虎钳剪铁丝和用剪刀剪线的例子同样可用圣维南原理说明。

2.2020年年初，武汉发生了新型冠状病毒疫情。为了避免病毒的传播，政府对武汉采取了封城的措施，以减少冠状病毒对其他地方的影响。这个概念也与圣维南原理的思路十分吻合。

3.矩形浅梁的纯弯曲问题、矩形浅梁受均布荷载作用问题，在梁的两端（次要边界）的应力边界条件无法精确满足时，可用圣维南原理，使该边界上应力的合力（含合力矩）满足边界条件，即使边界上正应力的合力等于边界上的轴力、剪应力的合力等于边界上的剪力、合力矩等于边界上的弯矩。

4.薄板小挠度弯曲问题的板边为自由边时，其边界条件同样可应用圣维南原理进行处理，即使边界上的扭矩等效为剪力，再与边界上的实际剪力迭加，用此总剪力来满足剪力的边界条件。

5.在外半径远大于内半径的圆环受均部内压作用时，其极坐标下的应力分量为：σr=   qa，σθ=    qa，其中a为圆环内半径、r为径向坐标、qa为均布内压集度。显然，均部内压为平衡力系，当r很大时（即离平衡力系较远时），应力分量σr和σθ均很小，符合圣维南原理的第二种提法。

四、圣维南原理教学中的课程思政

课程思政是将思想政治教育融入学科教育的一种教育形式，是指将高校思想政治教育融入课程教学和改革的各环节、各方面，实现立德树人的有效途径。这就需要教师寻求各科教学中专业知识与思想政治教育内容之间的关联性，并在课程教学开展过程中，将思想政治教育的相关内容融会于学科教育当中，通过学科渗透的方式达到思想政治教育的目的。为此，在圣维南原理教学中，可挖掘如下素材。

1.圣维南原理由法国力学家圣维南于1855年在大量实验的基础上提出，但他未给出原理的证明。目前虽然有些学者试图证明圣维南原理，但从发表的论文来看，他们仅仅是对一些特殊情况给出了证明，而未对一般性的理论进行严格的证明。在讲授圣维南原理后，可向学生提供以上信息，并指出若学生今后能够通过努力钻研证明圣维南原理（一般性的理论证明），则以后该原理将可能不再叫圣维南原理，而用证明了圣维南原理的学生的名字來命名。由此，不仅活跃了课堂气氛，而且激发了学生对圣维南原理的求知欲，同时取得良好的教学效果。

2.通过圣维南原理的概念可以知道，集中力作用点会有应力集中问题，导致结构局部应力很大，对结构造成危害。所以，从结构受力有利的角度看，尽量将外力分散布置是较好的结构方案。此概念引申到学生的学习上，大部分学生采用平时不抓紧时间、马马虎虎，在考试前进行突击的方式，对其掌握课程知识是不利的，这也是力学课程挂科率居高不下的原因之一。所以，科学的学习方式应该是平时上课就认真投入，课后及时复习，把疑问在课堂或当天课后解决。通过将圣维南原理与学生学习相联系，培养学生树立正确的学习态度，加深学生对课堂知识的理解。

3.圣维南原理在弹性力学求解中主要用于处理次要

边界的边界条件，使难以满足的处理次要边界的边界条件得以近似满足。由该思路引出科学研究的方法论——“抓大放小法”，即分清主次，抓住主要矛盾，搞好宏观控 制，对次要矛盾进行微观调节（删繁就简——抓大保证了问题的主要特征，放小使问题得到简化）。告知学生，这个方法论在力学分析中有着广泛的应用，如“材料力学”“弹性力学”的基本假设、薄板弯曲问题的自由边界条件中的等效剪力以及平面应力问题和平面应变问题等的处理思路均包含“抓大放小法”，由此培养学生分析问题、解决问题的能力，从而达到授人以渔的教学目标。

参考文献：

[1]徐芝伦.弹性力学[M].北京：高等教育出版社，2005：1.

[2]蒋红雨.课程思政的教与学[J].黑龙江教育（理论与实践），2020，74（6）：6.

编辑∕李梦迪

作者简介：陈玉骥（1962—），男，海南文昌人，佛山科学技术学院土木工程系教授，博士，研究方向：弹塑性理论及应用。

基金项目：2020年广东省教育厅研究生示范课程建设项目“弹塑性理论”（2020SFKC064）;2020年佛山科学技术学院

“课程思政”教改立项建设项目“结构力学”;2019年佛山科学技术学院研究生重点课程建设项目“弹塑性理论”