考虑柔性负荷接入技术的智能电网线路规划模型构建*

曹 祯

(1.国网上海电力设计有限公司，上海 200001；2.上海交通大学 电子信息与电气工程学院，上海 200240)

0 引言

与传统电网相比，智能电网利用先进技术提高了电网多个方面的性能，包括电网可靠性、电能利用率、电能转换效率和供电质量等[1].智能电网运行的过程中涉及控制技术、传输技术和分布式数据传输技术等.智能电网在建设过程中的重要内容是线路规划，良好的线路规划可以提升电能输送效率与电能质量，从而保证电力市场的稳定，所以对智能电网线路进行规划具有非常重要的研究意义[2].

肖楚飞等[3]提出基于慢同调理论的电网线路规划方法，该方法在慢同调理论的基础上根据总线路数和弱连接线路数计算弱连接系数，以此构建电网线路规划模型，结合惯性权重和自适应变异的粒子群算法以及拓扑连通修复策略求解该模型，实现电网线路的规划，但是该方法没有考虑工业高载能负荷，导致规划的电路覆盖率较低.陶莉等[4]提出基于拉格朗日对偶算法的电网线路规划方法，该方法将成本最小化、用户效用最大化作为目标函数，以此构建电网线路规划模型，利用拉格朗日对偶算法对模型求解，最终实现电网线路的规划目标，但是该方法没有考虑智能电网中存在的商业聚合负荷，线路规划后的信号强度较低.樊金柱等[5]提出基于适应性指标的电网线路规划方法，该方法根据电网结构选取适应性指标，以此为依据构建电网线路规划模型，针对不同电网规划方案，利用主成分分析法进行相关规划方案决策，实现电网线路的规划，该方法在规划电网线路之前没有考虑居民智能家用负荷，导致智能电网线路的传输性能较差.

为了解决上述方法中存在的问题，提出考虑柔性负荷接入技术的智能电网线路规划模型构建方法.

1 柔性负荷接入

构建智能电网线路规划模型之前，对智能电网中不同类型的柔性负荷接入进行分析.

(1)工业高载能负荷

通过下式描述工业高载能负荷参与智能电网线路规划的具体过程：

Pfl1，n=ηfl1-1,nμonPl1-ηfl1-2，nμoffPl1

(1)

式中：Pfl1，n为第n个时间段内该类型负荷在智能电网线路规划过程中的有功功率；μon为激励系数；Pl1为该类型柔性负荷在用电区域内的功率总值；μoff为该类型柔性负荷的中断潜力系数；该类型负荷是否参与智能电网线路的规划由决策系数ηfl1-1，n、ηfl1-2，n决定[6]，通常情况下决策系数满足以下条件：

(2)

式中：Pload，n为第n个时间段内的风力发电功率；PWT，n为风力发电在第n个时间段内的负荷功率.

设Cfl1，n为工业柔性负荷在第n个时间段内产生的补偿成本，则补偿成本函数表达式如下：

(3)

式中：Δt为某一固定时间段；CPoff为该类型负荷在电网线路规划过程中的补偿单价；CPon为该类型负荷在电网线路规划过程中的激励补偿单价.

(2)商业聚合负荷

商业聚合负荷可以充分反映中小型商业用户的需求[7]，通过下式描述商业聚合负荷参与智能电网线路规划的过程：

Pfl2,n=-ηfl1-2,nkBcutμBcutPl2

(4)

式中：Pfl2,n为第n个时间段内该类柔性负荷参与智能电网线路规划的有功功率；μBcut为潜力系数；kBcut为负荷消减比例，式中的决策系数ηfl1-2,n满足下列条件：

(5)

假设Cfl2,n为第n个时间段内该类柔性负荷对应的补偿成本，则补偿成本函数的具体描述如下：

Cfl2,n=ηfl1-2,nCP,Bcut|Pfl2,n|Δt,

(6)

式中，CP,Bcut为补偿单价.

(3)居民智能家用负荷

在智能电网飞速发展的背景下，居家智能电表被广泛地应用在居民家庭中，电网系统可以通过智能电表获取居民的电网需求信息，以此为依据规划智能电网线路[8].该类型柔性负荷参与智能电网线路规划产生的有功功率Pfl3,n可利用下式计算得到：

Pfl3,n=Pl3(ηpy,nμpy-ηfl1-3,nkHcutμHcut)

(7)

式中：Pl3为该类柔性负荷在用电区域内的总值；kHcut为负荷消减比例；μpy为平移潜力系数；该类柔性负荷是否参与智能电网线路规划由决策系数组ηpy,n、ηfl1-3,n决定，ηpy,n、ηfl1-3,n通常情况下符合下述公式[9]：

(8)

设Cfl3,n为第n个时间段内该类柔性负荷产生的补偿成本，其表达式如下：

(9)

式(9)为该类柔性负荷对应的补偿成本函数，其中CP，Hcut为消减补偿单价；CP，py为平移补偿单价.

根据上述计算结果对智能电网的总运行成本C进行计算：

(10)

式中，Cg,n为发电成本.

2 智能电网线路规划模型

2.1 模型构建

考虑柔性负荷接入技术，将通信可靠性和链路成本作为约束指标，构建智能电网线路规划模型.

通过提升站点成环率和路由可靠性可以保障电力传输网模型的可靠性，所有的链路都对应着不同的可靠性指标，且链路使用时间和工作时间可通过计算得到[10]，通过下式描述路由可靠性：

(11)

式中：φ为可靠性指标数量最大值；vj为最小业务路由值.

在此基础上可以利用站点数N和成环站点数C对成环率进行计算，结果用R=C/N表示.

网络拓扑结构的紧密度可以由成环率反映，网络的可靠性随着成环率增大而变高，当链路出现故障时电网系统仍然可以正常工作[11]，设U代表的是网络可靠性，可通过成环率和链路可靠性计算得到：

U=λ1L+λ2R，

(12)

式中：λ1为链路可靠性L对应的权重；λ2为成环率可靠性R对应的权重.

所有的链路成本都由运营成本和建设成本构成[12]，设F代表的是智能电网线路规划的成本，其计算公式如下：

(13)

式中：oi为线路在运营过程中产生的成本；ci为线路建设成本；当变量xi为0时，表明线路i没有被选中，当变量xi为1时，表明线路i被选中.

在上述约束下，构建智能电网电路规划模型：

(14)

2.2 模型求解

在构建考虑柔性负荷接入技术的智能电网线路规划模型后，采用改进小生镜遗传算法求解智能电网线路规划模型，具体过程如下：

(1)连通性检验并修正个体

为了获取更多的模型可行解，本文主要利用连通性检验方式随机产生个体，并对独立消亡和孤岛的不连通个体进行检验，以此完成个体修正[13].

(2)产生初始种群

计算修正后个体对应的目标值，并根据目标值大小对其进行排序，在此基础上选取前M个目标值较大的个体构成初始种群.

(3)选取适应度函数

通过下式计算个体的适应值F，并根据计算结果淘汰不符合要求的个体：

(15)

式中：F(x,y)为最小化目标值；Cmax为合理目标值的最大值.

(4)逆转操作

后期群体通常趋于一致，为了解决这个问题，本文通过逆转操作随机选取的较差个体，以此提高个体在后期的多样性，并增强算法在求解智能电网线路规划模型时的局部寻优能力[14].

(5)补算操作

利用变异操作获取个体的子体时，有可能产生劣质个体，为了提高个体的质量，需要对其进行补算操作[15].

(6)小生镜淘汰运算

小生镜淘汰运算的实质就是对个体群体中的海明距离||Xi-Xj||进行计算：

(16)

式中，xik、xjk为群体中存在的个体，当海明距离小于预先设定的距离Q时，对比个体之间的适应度，惩罚适应度较低的个体：

(17)

式中，q为惩罚项.通过上述过程保留下来的个体即为智能电网线路规划模型的最优解，输出最优解，实现智能电网的线路规划.

3 实验与分析

为了验证考虑柔性负荷接入技术的智能电网线路规划模型构建方法的整体有效性，需要对该方法进行测试.

测试区域有110 kV变电站3座，分别为变电站1、变电站2、变电站3，10 kV中压线路16条，其中从变电站1出线5条，变电站2出线7条，变电站3出线4条.新建110 kV变电站1座，新增10 kV线路10条.

为了方便统计，对现有线路进行编号，结果如表1所示.

表1 线路编号

原有线路以及计划新建线路的负荷情况如表2所示.

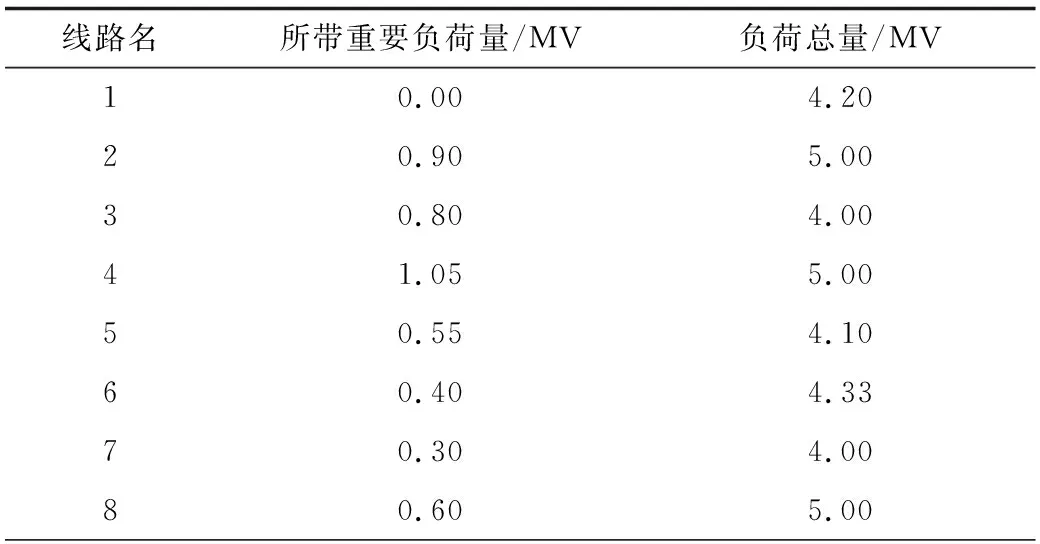
表2 负荷情况

表2(续)

将本文方法应用至该区域的智能电网线路规划中，则规划效果如图1所示.

图1 规划效果Fig.1 Effect of planning

分析图1可知，采用本文方法进行智能电网线路规划后，线路覆盖率增加，各变电站之间的联系加强，且不存在独立线路，说明考虑柔性负荷接入技术的智能电网线路规划模型应用效果更好.

将覆盖率、信号强度和传输性能作为测试指标，测试考虑柔性负荷接入技术的智能电网线路规划模型构建方法(方法1)、基于慢同调理论的电网线路规划方法(方法2)和基于拉格朗日对偶算法的电网线路规划方法(方法3)的整体有效性.

(1)线路覆盖率

不同方法的线路覆盖率如图2所示.

图2 线路覆盖率Fig.2 Line coverage

分析图2中的数据可知，在不同区域中方法1规划的智能电网线路的覆盖率较高，均达到80%以上，方法2和方法3规划的智能电网线路的覆盖率在60%上下波动，说明这两种方法规划的线路无法覆盖一些用电区域.对比测试结果可知，方法1规划的智能电网线路覆盖率最高，因为方法1在构建智能电网线路规划模型之前，对不同类型的柔性负荷进行了分析，根据不同区域的柔性负荷规划智能电网线路，提高了线路的覆盖率.

(2)信号强度

不同方法的信号强度测试结果如图3所示.

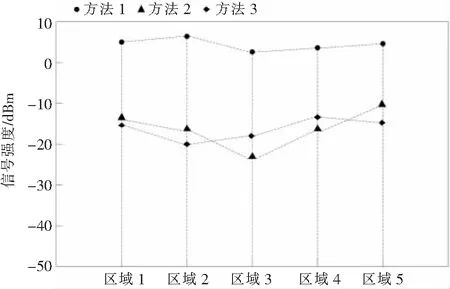
图3 信号强度Fig.3 Signal strength

分析图3中的数据可知，不同区域接收的信号强度在不同方法中的差异较大，方法1规划的智能电网中各区域的信号强度较高，方法2和方法3规划的智能电网中各区域的信号强度较低，因为方法1分析了不同区域的柔性负荷，并根据分析结果进行了负荷补偿，提高了信号接收区域的信号强度.

(3)传输性能

不同方法的传输性能测试结果如图4所示.

图4 传输性能测试结果Fig.4 Transmission performance test results

分析图4可知，随着传输距离的增加，方法1的信号强度基本保持不变，且信号强度处于平稳状态，说明信号基本不受传输距离的影响；随着传输距离的增加，方法2和方法3的信号强度有所降低，且信号强度波动较大，表明以上两种方法的信号强度受传输距离的影响较大.根据测试结果可知，方法1的传输性能较好，因为方法1在电网柔性负荷的基础上将通信可靠性作为约束条件，构建智能电网线路规划模型，保障了电网通信的可靠性，提高了智能电网的传输性能.

4 结束语

电力网络的规模、业务数量和业务种类随着智能电网的发展不断增加，为了满足用户的业务需求，以及电力通信网络的经济高效性和可靠性，需要对智能电网的路线进行规划.目前智能电网线路规划方法存在线路覆盖率低、信号强度差和传输性能差的问题，提出考虑柔性负荷接入技术的智能电网线路规划模型构建方法，对智能电网不同类型的柔性负荷进行重点考虑，以此构建智能电网线路规划模型，通过求解模型实现智能电网线路的规划.实验结果表明，该方法提高了智能电网的线路覆盖率及信号强度，并优化了传输性能，为智能电网的发展奠定了基础.