经验模态分解神经网络的研究与应用

包志强，王 美，黄琼丹，吕少卿

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

0 引 言

卷积神经网络[1-8]对一维信号进行识别主要有两种形式。一种是直接使用原始一维时序信号作为卷积神经网络(convolutional neural network，CNN)的输入，通过卷积层的滑动卷积操作自动获取信号的瞬态特征，无需任何人工提取特征进行信号的识别[9-12]，这种方式仅仅对信号的整体特征进行了提取，忽略了信号内部的特征信息。另外一种方式是将卷积神经网络与其它经典算法相结合进行信号识别，如平稳小波变换与CNN结合[13]、短时傅里叶变换与CNN结合[14]，但是小波变换和短时傅里叶变换需要预先选择合适的基函数，具有一定的局限性。文献[15]和文献[16]将EMD算法与CNN相结合，利用经验模态分解(empirical mode decomposition，EMD)算法将信号进行分解，结合CNN提取特征进行信号识别。EMD的自适应分解特性有利于信号的分解，但是上述方法是使用EMD算法首先对信号进行处理，将处理后的信号进行作为卷积神经网络的输入，并没有实现EMD算法与卷积神经网络的紧耦合。

本文提出了一种EMDNN(empirical mode decomposition neural network)模型，将EMD算法与卷积神经网络进行紧耦合，按照每一个本征模函数(intrinsic mode function，IMF)特征信息的重要性将不同时间尺度的局部特征信号进行自适应加权重构完成特征的提取，增强了网络模型在时域提取特征的能力，提高了网络模型对信号的识别准确率。

1 相关算法理论

1.1 经验模态分解

1998年，Huang提出了经验模态分解算法，算法的本质就是产生一系列不同尺度的本征模函数和一个残余分量。分解的原理是基于信号序列时间尺度的局部特性，无需预先设定任何基函数，将组成原始信号的各尺度分量不断从高频到低频进行提取，则分解得到的本征模函数是按频率由高到低进行排列的，即首先得到最高频的分量，然后是次高频的，最终得到一个频率接近为0的残余分量。

EMD算法分解数据的要求参见文献[17]。这种分解方法是通过数据的时间尺度特征来获得本征波动模式，然后分解数据，分解过程可以形象地称之为“筛选”过程，该筛选过程实现了使复杂信号分解为有限个本征模函数，使非平稳信号自适应转化为平稳信号，各本征模函数包含了原信号的不同时间尺度的局部特征[18]。EMD算法在理论上可以应用于任何类型信号的分解，因而在处理非平稳及非线性数据上，具有非常明显的优势。

1.2 卷积神经网络

卷积神经网络具有强大的学习能力和高效的特征表达能力，广泛应用于图像、信号识别等领域。LeNet-5[19]是经典的卷积神经网络，包含了神经网络的基本模块：输入层、卷积层、池化层、全连接层和输出层[20]。卷积层通过卷积核在输入数据上进行滑动，完成特征的提取。池化层对提取到的特征进行下采样，保留主要特征，去除冗杂信息，减少计算量。全连接层通过加权对学习到的特征进行重组，将学习到的特征映射到标签空间。多分类时输出层通常采用Softmax层，将全连接层的输出映射为区间(0,1)的概率值，数值最大的类别即为预测的结果[21]。

2 网络模型

2.1 EMDNN模型

LeNet5相对于其它深度学习网络模型具有结构简单、参数少的优点。因此，本文基于经典的LeNet5模型结构，将EMD算法与卷积神经网络进行紧耦合，提出EMDNN模型如图1所示，其中L表示输入信号的长度，N表示每个信号在EMD层分解为IMF的数量，S表示EMD1层特征图的数量，T表示EMD2层特征图的数量，p和q表示池化后信号的长度。

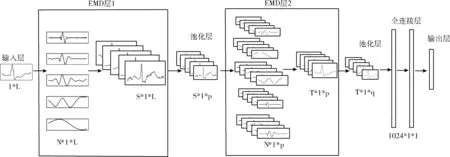
图1 EMDNN网络模型

EMDNN模型将传统卷积神经网络的卷积层替换为EMD层，由输入层、两个EMD层、两个池化层、两个全连接层、一个输出层构成。输入信号在EMD层按照时间尺度特征进行自适应分解，分解后的各个本征模函数代表着不同的时间尺度特征，按照其重要性进行自适应加权重构，实现特征的提取。EMD1层采用S组权重，EMD2层采用T组权重，全连接1层和全连接2层均采用1024个权重对提取的特征重组。完整的算法流程为：

(1)输入长度为L的一维信号；

(2)将信号自适应分解为N个IMF，采用S组随机初始化权重对IMF进行加权重构提取特征，加偏置后，采用tanh函数激活；

(3)对S个1*L的特征信号进行最大池化降维得到S个1*p的特征信号；

(4)对输入EMD2层的每一个1*p的信号进行自适应分解，采用T组随机初始化权重对IMF进行加权重构，加偏置后使用tanh函数激活，得到T个1*p的特征信号；

(5)对T个1*p的特征信号进行最大池化降维得到T个1*q的特征信号；

(6)将池化后的特征信号经过全连接层进行特征综合后通过Softmax层映射，输出最大概率的数值所属类别即为分类结果。

2.2 EMDNN特征提取算法

一维信号经过EMD层的自适应分解后，得到多个不同频率的IMF和一个残差(Residue，Res)，各IMF以及Res中都包含了原信号不同时间尺度的局部特征信息。虽然有效信息主要包含在高频IMF中，但在实际情况中，低频IMF以及残差中也含有原始信号的局部特征信息。如果只是选择高频IMF进行信号的重构，得到的特征信息将会丢失原信号中的一些特征信息，进一步影响信号的识别，因此本文的算法中保留所有IMF和残差。考虑到不同频率的IMF和残差中包含的局部特征信息对信号识别的重要性不同，本文引进权重W，最优的权重W将由网络模型学习得到。将分解得到的所有IMF和Res按照其特征信息的重要性进行自适应加权重构，得到的重构信号将是各个时间尺度信息的有效组合，完成信号特征的提取。采取多组权重，对IMF进行重构将得到多个不同的特征信号。END层将信号自适应分解为N个IMF和一个残差后，对IMF和残差进行自适应加权重构提取特征，其分解和重构提取特征过程如图2所示。

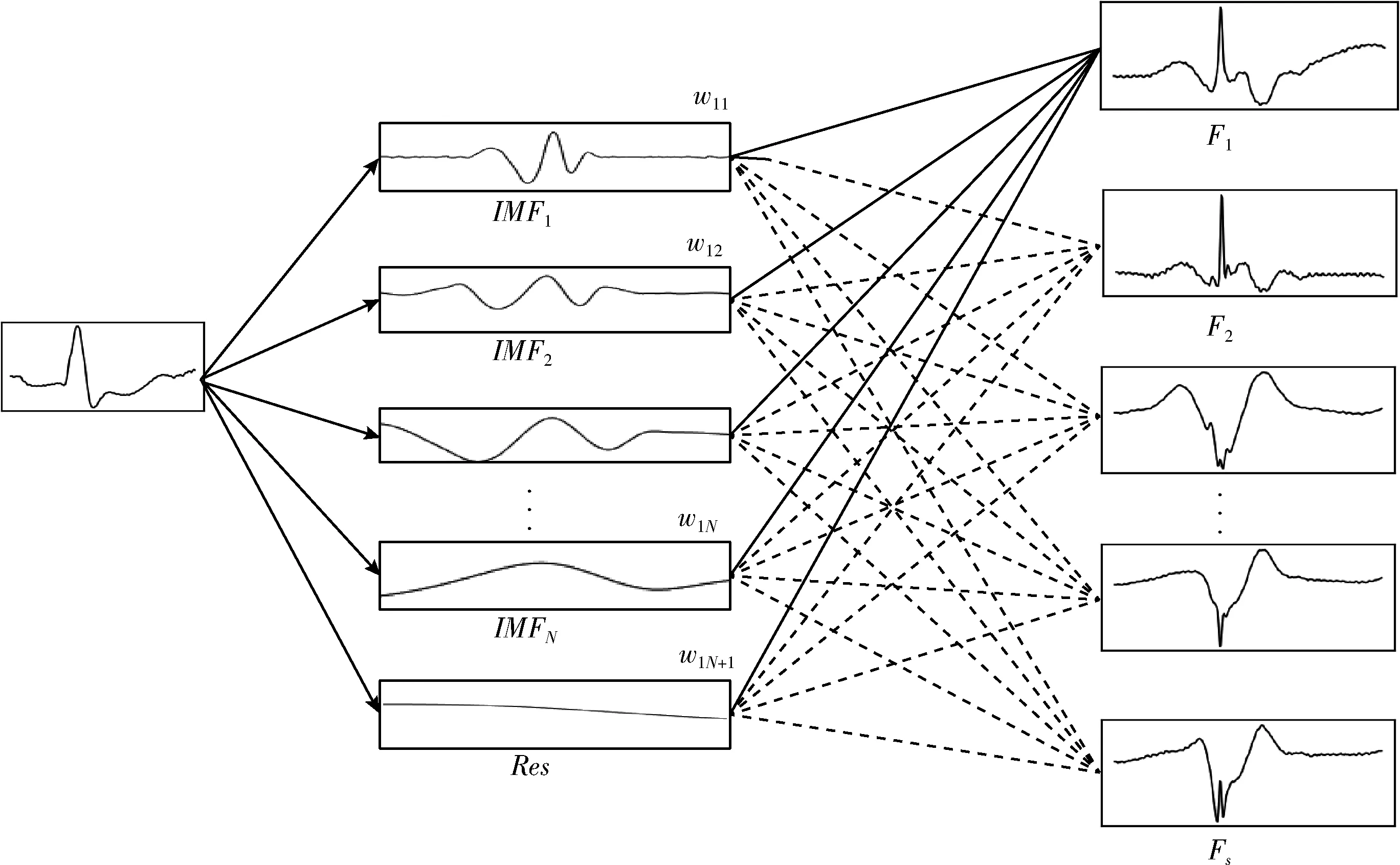
图2 EMD层信号分解与加权重构提取特征

EMD层信号特征提取算法流程如下：

(1)输入一维信号S(t)；

(2)找出S(t)的极大值点和极小值点，使用3次样条函数插值，得到上下包络线u(t)和l(t)；

(3)计算上下包络线的均值m(t)如式(1)所示

(1)

(4)计算S(t)与m(t)的差值h(t)=S(t)-m(t)；

(5)若h(t)是IMF函数，则令IMF(t)=h(t)，并转入(6)，否则令S(t)=h(t)并转入(2)；

(6)从S(t)中分离IMF(t)，得到r(t)=S(t)-IMF(t)，若r(t)满足分解条件，令S(t)=r(t)并转入(2)进行下一轮分解，否则转入(7)；

(7)分解结束，分解获得的N个IMF和Res构成矩阵，IMF=[IMF1,IMF2,…,IMFN，IMFN+1]，式中IMFN+1表示残差Res；

(8)随机初始化S组权重构成矩阵W如式(2)所示

(2)

(9)加权重构得到i个特征向量构成特征矩阵如式(3)所示

(3)

式中：wij表示第i组权重中的第j个权重参数，Fi表示IMF与第i组权重wij重构后得到的第i个特征向量。

(10)使用交叉熵损失函数，由网络反向传播学习更新权重wij，获得最优权重参数。

3 实 验

3.1 实验数据

3.2 评价指标

本文采用召回率、精确率和准确率作为评估算法性能的度量指标，分别表示为式(4)、式(5)和式(6)

(4)

(5)

(6)

其中，TP和FN分别表示为正样本和负样本被正确分类的个数，TN和FP分别表示为正样本和负样本被错误分类的个数。

3.3 实验结果

本文实验中输入心电信号的长度N为250个采样点，EMD层参数N值为4，即在EMD层进行自适应分解后得到4个IMF和一个Res，EMD1层权重S设置为32，EMD2层权重T设置为64，激活函数选择tanh函数，池化方式为步长为2的最大池化，损失函数使用交叉熵损失函数，迭代次数为1000次。

为验证本文模型的有效性，采用CNN模型进行对比实验。分别使用本文提出的网络模型和CNN模型对心电信号进行特征提取，经过CNN模型卷积层提取到的部分特征如图3所示，经过EMDNN模型EMD层加权重构后提取到的部分特征如图4所示。

由可视化的特征图可知，EMDNN模型经过EMD层自适应加权重构得到的特征信号相对于CNN卷积层滑动卷积提取到的特征信号具有更多的形态，说明了其提取到了更多的时域特征。

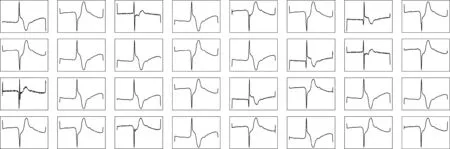
图3 CNN卷积提取的特征

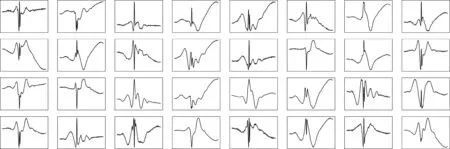
图4 EMDNN自适应加权重构提取的特征

将提取到的特征信号经过全连接层进行重组后输入到Softmax层进行信号类别的预测，本文提出的EMDNN模型和CNN模型对心电信号分类结果的混淆矩阵见表1，损失(Loss)与准确率(Accuracy)曲线如图5所示，其中T表示信号真实的类别，P表示信号预测的类别。

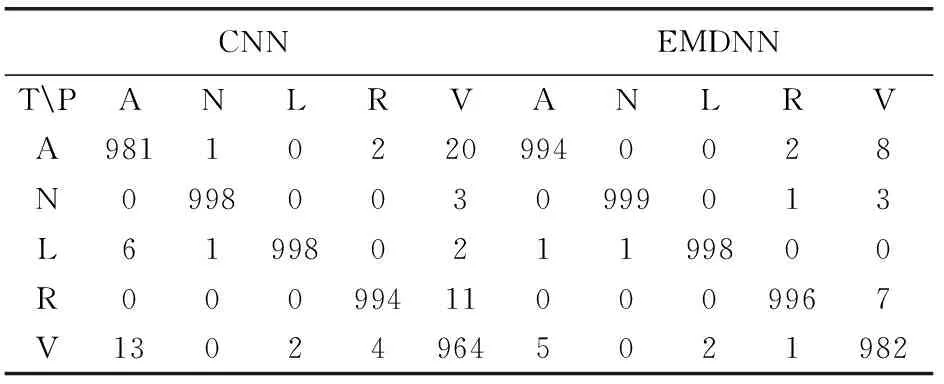
表1 EMDNN与CNN模型识别结果混淆矩阵

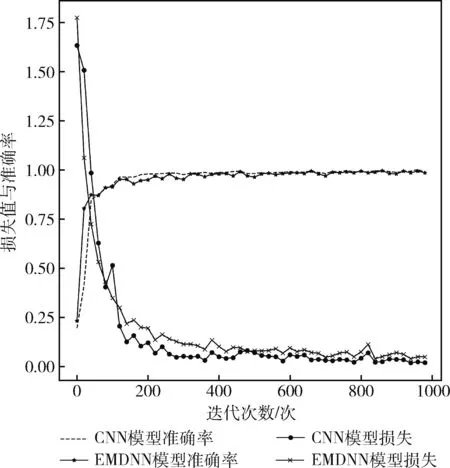
图5 Loss与Accuracy曲线

从表1的混淆矩阵中可以看出网络模型识别结果的分布情况，对角线上是各类别信号正确预测的个数，其余均为错误预测个数。由混淆矩阵可知，EMDNN模型和CNN模型对于N、L、R这3类信号的识别正确率较高，均达到99%以上。EMDNN模型对于A类和V类信号预测的正确个数高于CNN模型。

从图5所示的Loss与Accuracy曲线可知，EMDNN模型在本实验数据集上具有较小的Loss值，Accuracy值与CNN模型下的Accuracy值持平。

为了更方便比较两个模型对心电信号识别结果，根据2个模型的混淆矩阵计算每一类别信号的Recall和Precision，并计算5个类别信号的平均Accuracy，结果见表2。

由表2可以看出，本文模型对A、N、L、R、V这5类心电信号的召回率略高于CNN模型，除N类和R类心电信号的精确率略低于CNN模型外，其它3类心电信号的精确率均略高于CNN模型，此外本文提出的模型对5类信号的平均识别准确率为99.38%，高于CNN模型的准确率98.70%。由于EMD层在提取特征的时候获取了不同时间尺度的时域特征，因此在时域波形相似的心电信号上可以提取到更丰富的特征信息，使得本文模型分类的准确率高于CNN模型。

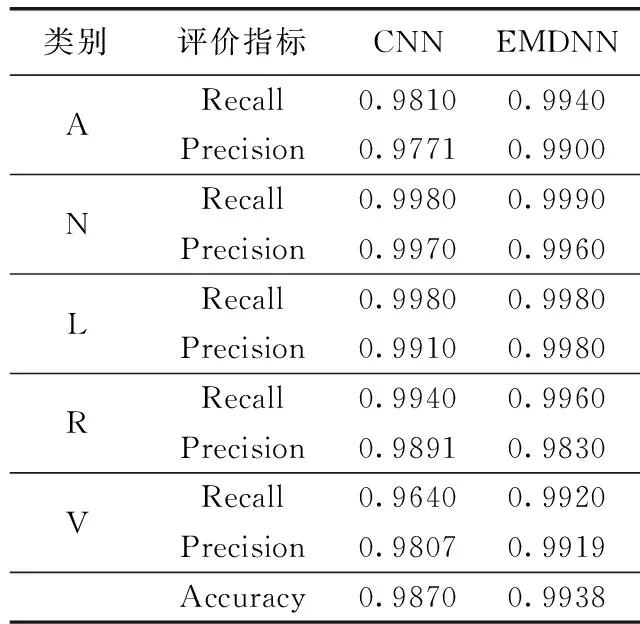
表2 CNN和EMDNN模型下各个类别信号的 召回率和精确率

机器学习算法是信号识别的传统方法，考虑到数据的特征维度不高，样本数量充足，因此使用心电信号数据的原始特征，将数据作为随机森林(random forest，RF)、K近邻(K-nearest neighbor，KNN)、支持向量机(support vector machines，SVM)3种分类器的输入进行识别分类。SVM分类器采用径向基核函数，gamma取值为0.2。KNN的参数K值设置为5，随机森林的决策树的数目选择为100，最小样本数量设置为2。RF、KNN和SVM在测试数据集上的准确率见表3，并和本文提出的模型进行结果对比。

表3 EMDNN和传统算法准确率对比

由表3实验结果可知，本文提出的网络模型识别准确率高于其它的传统算法，表明了本文提出的模型的有效性。

4 结术语

本文提出了一种EMDNN模型，在经典卷积神经网络模型的基础上，引入经验模态分解算法，实现了该算法与卷积神经网络的紧耦合。该模型保存了经典卷积神经网络所具有的结构，又利用了EMD算法处理非线性信号的优势，通过对一维非线性时序信号的不同时间尺度特征进行自适应加权重构，增强了其提取一维非线性信号时域特征的能力，提高了对一维非线性信号识别的准确率。在MIT-BIH心律失常数据库官方数据集上进行心电信号分类实验，结果表明本文提出的算法相对于经典卷积网络模型和传统机器学习算法具有较好的效果。