基于最小完成时间的车载边缘计算任务流卸载策略
2021-12-23晋士程丁洪伟
李 波,晋士程,丁洪伟,武 浩
(云南大学 信息学院,云南 昆明 650500)
0 引 言
基于传统云计算模式的车联网(internet of vehicle,IoV)面对海量终端接入时会造成网络拥塞,增加计算服务延迟[1]。而具备分布式、实时性和移动性特点的移动边缘计算(mobile edge computing,MEC)[2,3]能够就近为车辆提供所需计算服务,被认为是一种有效降低车载任务时延的方案[4,5]。
在车载边缘计算(vehicular edge computing,VEC)环境下,由于车辆的移动性,车辆与周围资源构成的网络拓扑结构具有不稳定性[6]。针对动态变化的资源如何合理地进行计算卸载是保证任务顺利且高效执行的关键。现有的研究通常利用车载自组织网将周边车辆作为卸载资源,比如文献[6-8]在VEC场景下,根据车辆的计算异质性、机动性,考虑车辆移动性可能导致的服务中断情况,为任务选择合适的车辆节点进行卸载。或是以路侧单元(roadside unit,RSU)作为卸载资源,例如文献[9-11]根据车辆移动速度、RSU覆盖范围、计算和通信资源的变化等实际条件,为任务选择最佳的RSU进行卸载。尽管现有研究对于VEC环境下的卸载策略取得了一定进展,但仍存在以下问题:①车辆应用模型多为单任务、离散任务或串行任务模型,对于复杂任务流模型的研究较少。②多数研究对于资源的利用较为单一,仅以RSU或仅以车辆作为代理资源。因此,在动态VEC环境下同时利用RSU和车辆作为代理资源,以最小完成时间为目标实现复杂任务流的卸载,是本文研究的重点。对此,本文通过不同复杂度的任务流建模求解,以任务属性和资源实时信息为依据对任务进行合理的映射,使得最终卸载策略具有较广泛的适用性。
1 系统模型
VEC体系主要由车辆携带的车载单元(on board unit,OBU)、RSU、边缘服务器(edge server,ES)和蜂窝网的BS、WLAN接入点组成,形成可以实现车车互联(vehicle to vehicle,V2V)、车路互联(vehicle to roadside,V2R)的无线网络系统[1]。其中,在V2R模式下,车辆可以通过无线网络访问部署在RSU上的ES[12],获取边缘服务器的信息和计算资源。在V2V模式下,车辆之间组成车载自组织网实现车辆之间的信息共享。
假定所有车辆都在单行道路上以自身速度匀速前行,生成任务的车辆为源车辆,其余为协作车辆,沿车辆行驶方向有多个RSU。每个车辆可以通过GPS和自身传感器与其它车辆和RSU进行速度、位置、资源使用情况等状态信息的实时共享,源车辆通过对这些状态信息的分析来确定自身任务是否需要卸载、何时卸载以及卸载至何处。在进行任务相关数据的传输时,车辆与RSU、RSU与RSU之间均通过移动无线通信网络进行连接,车辆与车辆之间通过DSRC(dedicated short range communications)实现通信,系统架构如图1所示。

图1 系统架构
建立车辆集合V={V0,V1,…,VX}, 其中V0代表源车辆。建立RSU集合R={R1,R2,…,RY},RY代表第Y个RSU。对于可卸载任务,供其选择的执行位置有本地资源和代理资源(包括协作车辆和RSU),建立所有资源集合p={p0,p1,p2,…,pM}, 其中p0为本地资源,p1~pM为代理资源。用ηim表示任务ni与资源pm的映射关系,当ni在pm上执行时ηim=1,否则ηim=0。
1.1 任务模型

图2给出了一个具体的以DAG表示的任务流示例,其中任务1是任务2的前项任务,任务3是任务2的后项任务。任务1和任务10分别为入口任务和出口任务,因而不可卸载。任务9需要获取任务3、任务6和任务8的输出结果才可以执行。
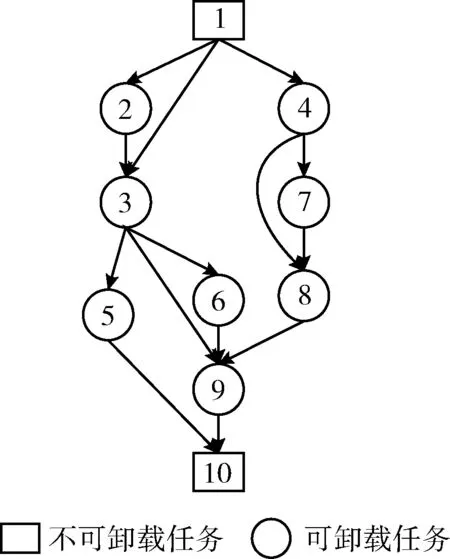
图2 DAG
1.2 通信模型
在VEC环境下,包括V2R和V2V的通信模式。其中,V2R是车辆与RSU之间的通信,V2V是车辆与车辆之间的通信。两种通信模式都会随着车辆的移动而发生通信链路的变化。
1.2.1 V2R通信模型
V2R通信模型参考文献[14]。假设d为车辆与RSU覆盖范围中心之间的距离,BVR为车辆与RSU之间的基础带宽,δ为路径损耗因子,ε为信道衰落因子,P0为车辆的传输功率,N0为噪声功率,根据香农公式可以得出V2R模式的传输速率为
(1)
由于车辆始终处于运动状态,d值时刻在变化。对于一个车辆而言,假设其刚好进入RSU覆盖边缘作为起始点,行驶速度为v,忽略道路宽度,则t时刻的d值为
(2)
其中,rR为RSU的覆盖半径,l为RSU覆盖范围中心到道路的垂直距离,如图3所示。

图3 V2R通信模型
车辆与RSU之间的传输速率是时刻变化的,将平均上传速率作为实际传输速率,则车辆在当前RSU覆盖范围内的V2R传输速率表示为
(3)
若车辆当前处于Rx的覆盖范围,需要与Ry(x≠y) 通信,因为各个RSU的位置是固定的,两个相邻RSU之间的传输速率sRR视为固定值。设两个RSU中间跳数为H,则此时通信速率为
(4)
1.2.2 V2V通信模型
单辆车可通信范围是以rV为半径的圆形区域,则车辆之间最大可通信距离为2rV。当车距在最大可通信距离内时,车辆之间以单跳的方式通信,如图4中的车辆A和车辆B。当车距超过2rV时,车辆之间不能直接通信,需要将其它可通信车辆作为中继点,以多跳的方式进行通信,如图4中车辆A和车辆C之间的跳数为2。

图4 V2V通信模型
两车之间通信速率表示如下
(5)
其中,BV2V是车载自组织网中的基础带宽,HM代表车辆之间通信的跳数。
1.3 运动模型
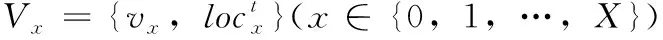
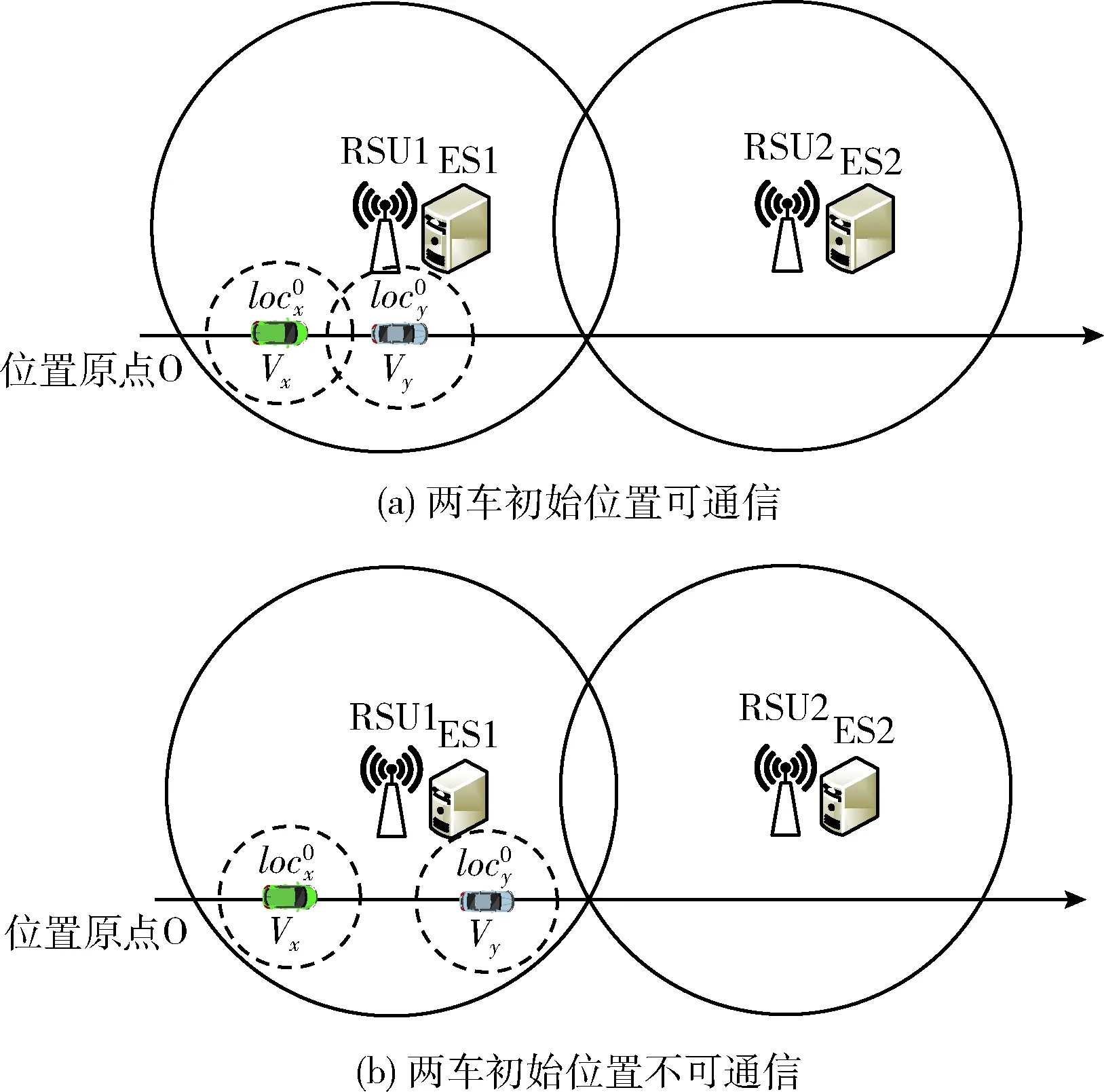
图5 两车初始位置通信状态
对于图5(a)所示情况:
若vx=vy, 则两车始终可以通信;
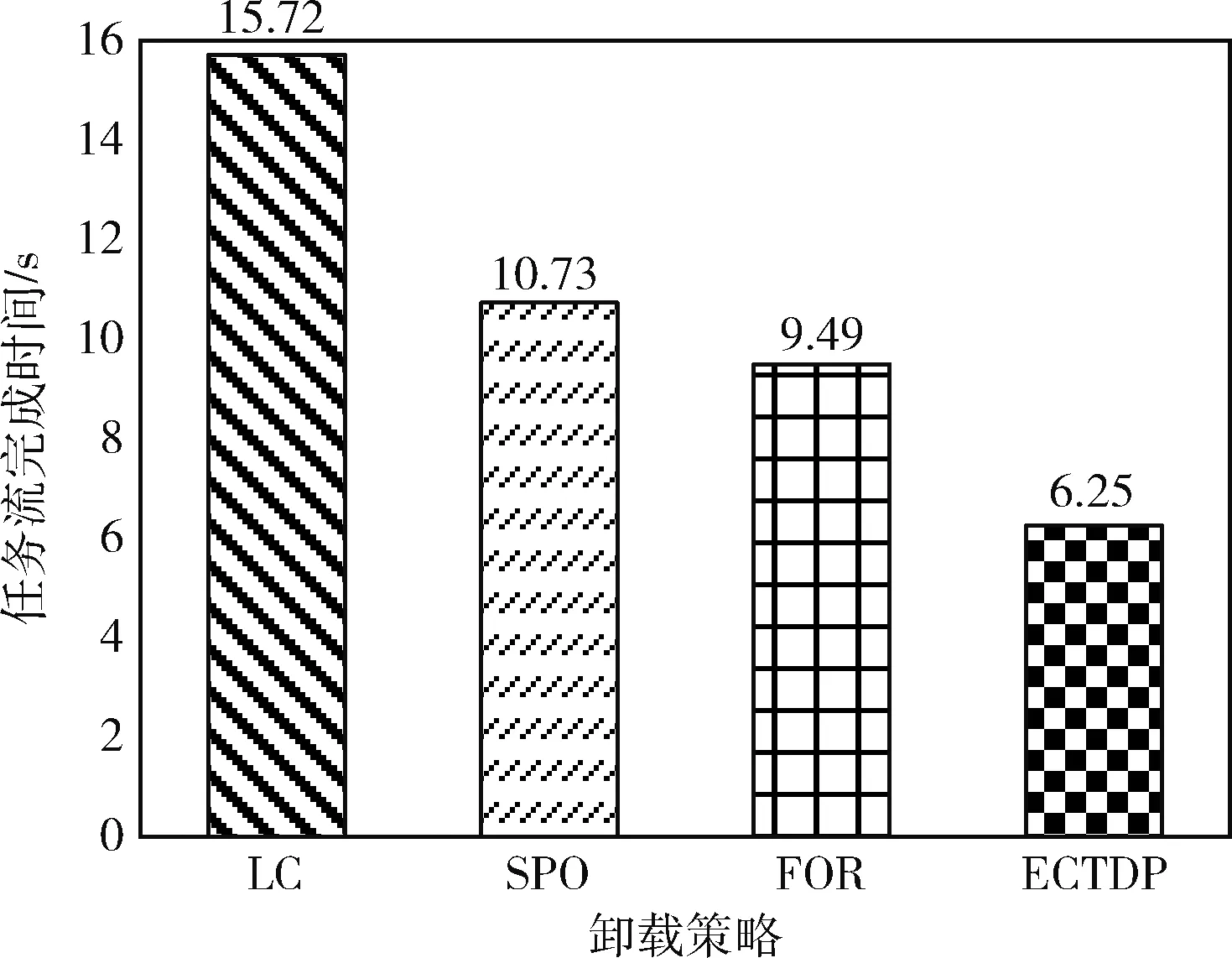
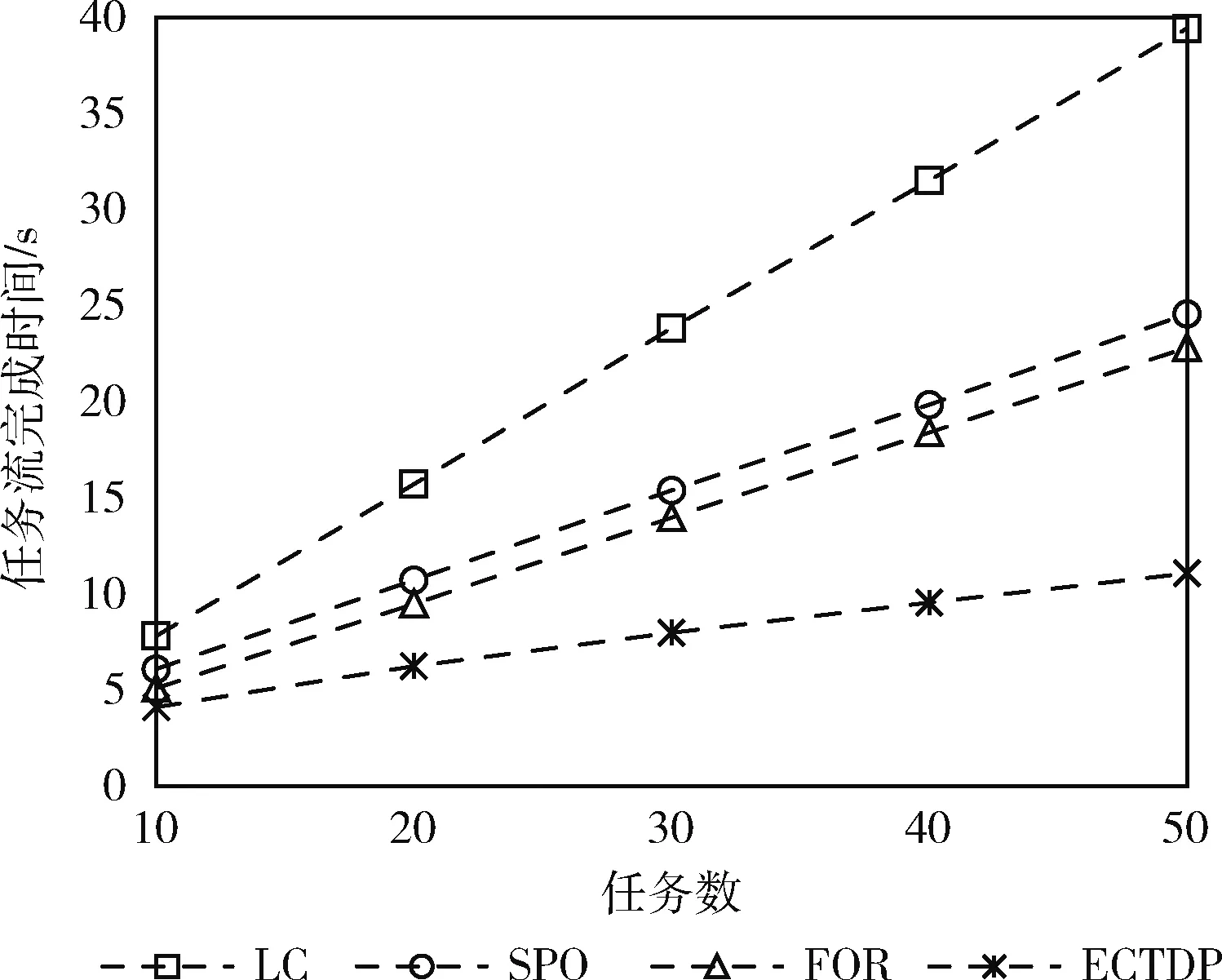
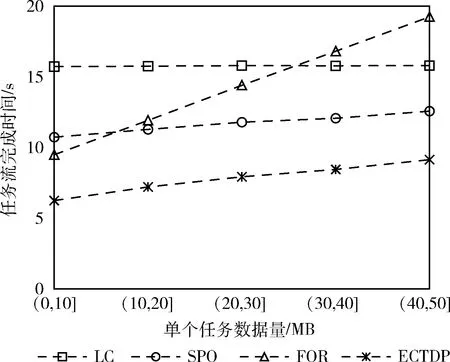
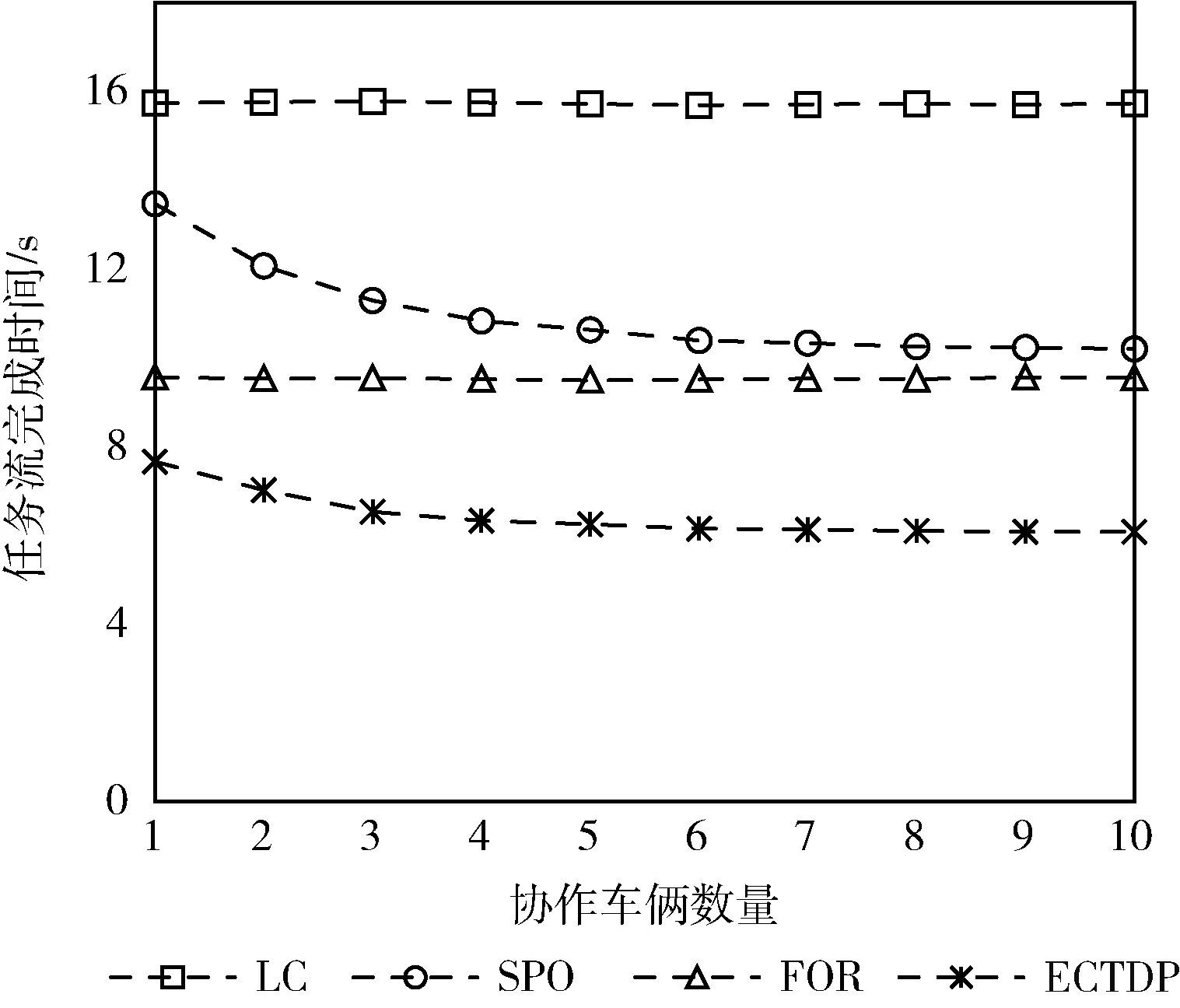
若vx t1=0 (6) (7) 车辆Vx和Vy的可用通信总时长ΔtVxVy为 (8) 若vx>vy, 则 t1=0 (9) (10) (11) 对于图5(b)所示情况: 若vx≤vy, 则两车始终不可通信; 若vx>vy, 则 (12) (13) (14) (15) 而对于V2R的通信,车辆Vx在第y个RSU覆盖范围内与Ry的可通信总时长ΔtVxRy为: 若当前RSU是车辆初始连接的RSU,则 (16) 否则 (17) (18) 将资源pm和pn之间的通信速率表示为rmn,对于同一资源,其内部传输速率设为无穷大,即相同资源上传输数据所需时长为0。则将一个任务ni卸载所需时长为 (19) 当资源pm的计算能力为fm时,执行计算所需时长为 (20) 待任务ni计算完成后将计算结果发送至nj所需传输时长为 (21) 若任务ni为入口任务,其开始执行的时刻STi和执行结束的时刻CTi分别为 STi=0 (22) (23) (24) CTi=STi+Tcal (25) 为任务流中的每个任务寻找最优卸载决策,其中包括是否卸载、何时卸载以及映射资源,目的是使得整个任务流的完成时间,即出口任务的结束时间最小,本文优化目标和约束条件表达如下 (26) 其中,约束条件C1表示一个任务只能在一个资源上执行,C2表示一个资源不能同时执行多个任务,C3表示任意两个连通的任务之间的依赖关系呈因果性。 任务的卸载与调度属于组合优化问题,而组合优化问题属于NP完全问题。面对任务间的约束关系和动态变化的网络拓扑结构,本文提出了一种基于动态优先级的最早完成时间的卸载策略ECTDP(earliest completion time based on dynamic priority),该策略可分为两个步骤:可用资源的选择、任务-资源的映射,主要思路流程如图6所示。 图6 ECTDP策略流程 由于车辆移动性会导致资源之间的通信链路发生变化,为了保证前项任务与后项任务之间的顺利传输以及源车辆将任务完整地卸载至目标资源,可靠的通信链路至关重要。此外,当一个任务有多个前项任务,资源的异构性和移动性必然导致这些前项任务在全部完成时,互相存在时间和空间上的跨度,而这种时空上的差异是影响后项任务执行状况的又一重要因素。因此,需要对一个任务的可用卸载资源进行筛选。所有车辆在单行道中匀速前行,因而每个车辆在每个时刻的位置都可以预测得知,以此作为解决问题的依据。在通信上,选择在传输期间通信链路稳定无变化的资源;在时间上,采用即执行完即传输的方式,实现时间的不间断利用和重叠利用;在空间上,为避免空间跨度过大,以源车辆的位置为准对周边资源进行选择,形成一个随源车辆移动且覆盖范围动态变化的可选区域。当一个任务nj已执行完毕,对其后项任务ni卸载资源的选择有以下3类: (1)nj在源车辆V0上执行,ni的可用资源有: (2)nj在协作车辆Vx(x≠0) 上执行,ni的可用资源有: (3)nj在Rx上执行,ni的可用资源有: 综上,当任务ni有多个前项任务时,每个前项任务基于上述3种情况进行可用卸载资源的选择,所有前项任务所选资源交集即为任务ni的可用卸载资源池。若无交集,说明当所有前项任务完成时,至少两个前项任务所选的RSU不同,此时仅以其中距离位置原点最远的RSU作为可用卸载资源池。 当一个任务的所有前项任务全部执行完毕,则该任务就绪。对于复杂任务流,同一时间可能有多个任务就绪。面对就绪任务的不断更新以及网络拓扑的动态变化,为了使任务流顺利执行且用时最短,合适的资源-任务映射关系尤为重要。仅将计算能力较强或通信速率快的资源作为任务的卸载目标较为片面,因为实际执行中各个资源的状态不同。另外,当多个无依赖关系的任务就绪,在有限的资源下,任务的调度顺序也是需要面临的问题。对此本文以任务在资源中的实际执行情况为依据进行映射。 在进行任务-资源的映射之前,首先根据任务之间的依赖关系,计算每个任务的b-level(bottom level),即任务到出口任务的最长路径长度,该值能够体现单个任务对整个任务流影响的重要程度,具体算法如下: 算法1:计算任务b-level值算法 (1)以任务流的逆向拓扑顺序建立任务节点列表List, 设任务ni的b-level值为BL(ni) (2)建立空集合B (3)for每个任务ni∈Listdo (4)ifni是出口任务then (5)BL(ni)=ci (6)else (7)for每个任务nj∈sub(ni)do (8) 计算BL(nj)+ci+mi的值, 并将该值放置集合B (9)endfor (10)BL(ni)为集合B的最大值 (11) 令B=∅ (12)endif (13)endfor 算法1中第(5)行代表出口任务的b-level值是其自身的节点权值。第(7)行至第(10)行表示一个任务的b-level值是该任务的节点权值、输出边权值与其后项任务中最大的b-level值三者之和。 对于每个就绪任务,在其自身的可用卸载资源池中,按照1.4节给出的时延模型计算在各个资源上的完成时间,并计算该任务的b-level与各完成时间的差值。该值体现任务自身属性与资源实际执行情况的匹配程度,以此作为评价各个任务优先级的标准,可以起到综合考虑且自适应动态变化的作用,具体算法如下: 算法2:ECTDP策略调度算法 (1)建立就绪任务集合RET、 可用资源池集合AP、 任务-资源映射集合TPM、 动态优先级值集合DP (2)初始化RET={nentry},AP=∅,TPM=∅,DP=∅ (4)whileRET≠∅do (5)ifRET={nexit}then (6) 将nexit放在本地执行 (7) 将nexit从RET中剔除 (8)else (9)DP=∅ (10)for每个任务ni∈RETdo (11) 寻找ni自身可用资源池APi (12)for每个资源pm∈APido (13) 计算ni在资源pm上的完成时间CTi,m (14) 计算DP(ni,pm)=BL(ni)-CTi,m (15)endfor (16)endfor (17) 取DP(ni,pm)值最大的任务-资源对, 将ni卸载至pm, 更新TPM (18) 将ni从RET中剔除, 更新Tmprepare和RET (19)endif (20)endwhile 算法2中第(14)行所得动态优先级值可能为正数、负数或0,但始终选择值最大的作为优先映射。当ni执行完毕,其后项任务中可能部分已就绪,此时第(18)行更新RET的操作包括加入新的就绪任务,将与旧的就绪任务同时参与下一轮迭代的对比。 本文以整个任务流的完成时间作为性能指标(式(26)),分别以任务数、任务流最大出度、单个任务计算量、单个任务数据量、协作车辆数量作为实验变量,在不同环境下与3种基准卸载策略进行对比,包括不卸载(local computing,LC),全部卸载至RSU(full offloading to RSU,FOR),以距离源车辆最近且能通信的单个车辆作为卸载资源进行部分卸载(some part offloading,SPO)[15]。 本文以单行道作为仿真场景,有一个源车辆,其生成一个任务流,沿车辆行驶方向有若干个RSU,满足任务流的整个执行过程可用。所有车辆初始位置都在第一个RSU覆盖范围内,初始位置和车速在各自区间内随机产生,服从均匀分布。单个任务的计算量、数据量和输出结果的数据量也在各自取值范围内随机产生,服从均匀分布。基础参数设置见表1[14]。 表1 参数设置 首先以上述参数进行基准实验,然后仅改变任务数、任务流最大出度、单个任务计算量、单个任务数据量、协作车辆数量这些因素中的其中一个,保持其余不变,利用控制变量法进行多组对比实验。对于每组参数的实验过程如下: (1)初始化车辆数量、速度和位置,设定环境参数,生成仿真环境; (2)根据任务数、最大出度、计算量和数据量随机生成一个任务流; (3)设置资源属性参数,生成资源模型; (4)各个车辆按照运动模型运动; (5)根据每个任务完成时刻,实时更新各个车辆的位置以及所有资源的使用情况; (6)依照不同策略进行卸载; (7)待该任务流执行完成,记录当前参数下各策略的任务流完成时间; (8)重复(1)到(7)过程,进行1000次仿真,求出各个策略完成时间的平均值作为该组实验结果。 3.2.1 基准实验 为了综合评价各卸载策略的优劣性,以基础参数作为经典仿真场景进行基准实验,实验结果如图7所示。 图7 基准实验结果对比 由图7可知,SPO策略比LC策略更优,因为SPO可以利用周边单个协作车辆进行分布式计算,相比完全在本地串行执行更节省时间。FOR策略比SPO策略更优,是因为FOR可以充分利用边缘端较强的计算能力,缩短了每个任务的计算时间。而ECTDP策略最优,是因为该策略将RSU和协作车辆作为选择目标,计算资源的形式不再单一,充分利用边缘端强大的计算能力和车载自组织网的分布式计算,实现V2V和V2R两种通信模式的优势互补、相互延伸。此外,在进行资源选择时以通信链路的稳定和减小时空跨度为核心思想,避免了通信链路的变化造成的计算切换和等待,增大了时间的利用率,降低任务间的传输时间。 具体而言,在ECTDP策略进行任务-资源映射时,单个任务的b-level值体现该任务对整个任务流的影响程度,是任务自身属性的呈现。任务在各资源上的完成时间体现了在各种因素影响下的任务实际执行情况,是资源实际状态的呈现。将两者的差值作为调度任务的标准,是考虑了任务和资源的各方面因素后的综合评价,体现了任务与资源的实际匹配程度。优先选择差值最大的任务-资源对,能够最大程度缩短单个任务的完成时间并且对任务流整体造成的影响最大。因此,ECTDP策略可以大大降低任务流的完成时间,相比LC、SPO和FOR策略分别缩短了60.24%、41.75%和34.14%。 3.2.2 任务数对任务流完成时间的影响 将任务数分别设为10、30、40和50进行对比实验,实验结果如图8所示。 图8 不同任务数的任务流完成时间 由图8可以看出,任务数越多,执行任务流越耗时。这是因为任务流的规模越大,整个任务流中需要计算和传输的数据也随之增加,为方便描述,将任务流中总的计算量和数据量统称为总工作量。由于总工作量是由多个子任务的相关量线性叠加而得,因此总工作量与总任务数近似呈线性正相关。而在有限的资源下,执行任务流所需时长也与总工作量近似呈线性正相关。故而随着任务数的增多,任务流的完成时间呈近似线性上升。此时FOR策略虽优于SPO策略,然两者差距始终较小。这是因为FOR利用边缘端的较强计算能力,相对于SPO能够节省任务的计算时间,但FOR的全部卸载又导致过多的通信开销。 此外,在当前的参数环境下,全部卸载使得节省的计算时间微大于额外的通信开销,两者综合作用下导致FOR相对于SPO的优势不明显。对于不同的任务数,ECTDP都可以在计算开销与通信开销之间以及任务与资源的供求关系上做出均衡,因而面对不同规模的任务流,其完成时间始终最短,相比LC、SPO和FOR策略平均缩短了63.12%,45.82%和39.14%。 3.2.3 任务流最大出度对任务流完成时间的影响 将任务流的最大出度分别设为总任务数的20%、40%、60%和80%进行对比实验,实验结果如图9所示。 图9 不同最大出度的任务流完成时间 由图9可知,随着任务流最大出度的增大,LC和FOR策略不受影响,而SPO和ECTDP会有轻微的上升变化。因为任务流的最大出度决定了一个任务所能连接的最多后项任务的数量,当最大出度值增大时,任务流的复杂度增大。此时任务流内部的传输增多,单个任务会有更多前项任务,其开始执行时间受影响因素较多,推迟执行的可能性增大。LC和FOR策略将任务集中在单个资源上执行,资源内部传输时长为0,因而不受影响。但SPO和ECTDP策略需要在不同资源上执行,资源之间有一定的传输时长。然而任务流中单个任务的输出结果量往往比较小,而且传输结果数据采用并行传输,不考虑通信竞争,因此最大出度的变化对整个任务流的完成时间影响较小。但在不同出度的影响下,ECTDP策略始终是完成时间最短的,相比LC、SPO和FOR策略平均缩短了57.66%,40.70%和30.32%。 3.2.4 单个任务计算量对任务流完成时间的影响 将单个任务的计算量分别设定为(0,2]、(4,6]、(6,8]和(8,10](×108cycle)进行对比实验,实验结果如图10所示。 图10 不同计算量的任务流完成时间 由图10可得,随着单个任务计算量的增加,整个任务流所需计算的数据增多,因此完成任务流所需时长会随之上升。相比实验3.2.2,可以看出当前实验参数下的FOR策略与SPO策略之间的差距逐渐增大。这是因为FOR策略的优势在于所选资源的计算能力较强,当只增加计算量不改变数据量时,节省的计算时间与额外通信开销的比值增大,FOR策略的优势也逐渐明显。而ECTDP策略在面对较大计算量的任务时,会通过分布式计算和卸载至计算能力较强的资源这两种方式对计算时间进行节省,使得任务流总完成时间最小,相比LC、SPO和FOR策略平均缩短了59.74%,43.18%和34.06%。 3.2.5 单个任务数据量对任务流完成时间的影响 将单个任务的数据量分别设定为(10,20]、(20,30]、(30,40]、(40,50](MB)进行对比实验,实验结果如图11所示。 图11 不同数据量的任务流完成时间 由图11可知,单个任务数据量的增加对LC策略无影响,而对于涉及到卸载的其余3种策略有影响,会增加它们的通信时长从而使得完成时间有所增长。其中FOR策略随着数据量的增加,逐渐成为性能最差的策略。因为当只增大数据量不改变计算量时,节省的计算时间与额外通信开销的比值减小,此时FOR的劣势会被放大。而部分卸载的SPO和ECTDP,会根据卸载量的大小进行判断,可以将卸载量大的任务留在本地执行,减少通信开销。其中ECTDP面对多个可卸载资源时能够动态地调节任务的调度顺序,在最大程度利用并行计算和减少通信开销之间进行权衡,以实现最佳的综合效果,相比LC、SPO和FOR策略平均缩短了50.56%,33.57%和44.16%。 3.2.6 协作车辆数量对任务流完成时间的影响 将协作车辆的数量从1增加至10进行对比实验,实验结果如图12所示。 图12 不同协作车辆数量的任务流完成时间 由图12可以看出,协作车辆数量的变化对LC和FOR策略无影响,因为这两个策略的执行与协作车辆无关。FOR和ECTDP策略会随着协作车辆的增多先减少执行时间,再趋于平稳。这是因为协作车辆的增加使道路内交通密度变大,源车辆能够连接到其它车辆的可能性变大,即增大了并行计算的可能性,从而缩短完成时间。然而此时任务流的最大出度为6,即同时就绪的可并行计算的任务最多为6个。因此随着协作车辆的继续增多,可用资源对于任务是一种供大于求的过饱和状态,使得任务流的完成时间不再有明显变化,从而趋于平稳。ECTDP策略受协作车辆影响的波动比SPO策略小,这是因为前者除了协作车辆还可以将RSU作为卸载资源,充分利用边缘端的强大计算资源。ECTDP相比LC、SPO和FOR策略平均缩短了60.03%,42.65%和34.47%。 本文针对车载边缘计算环境中的复杂任务流卸载进行了研究,考虑了任务依赖关系、车辆的移动性、资源的异构性、资源的使用状况以及通信网络拓扑结构的变化等因素,提出了一种基于动态优先级的卸载策略,充分的实验表明,本文提出的策略相较于其它策略性能始终最优。在未来的研究中,将重点研究车载边缘环境中在满足任务流完成时间最小的同时降低源车辆的能耗开销,实现卸载策略的多目标优化。

1.4 时延模型

2 卸载调度策略
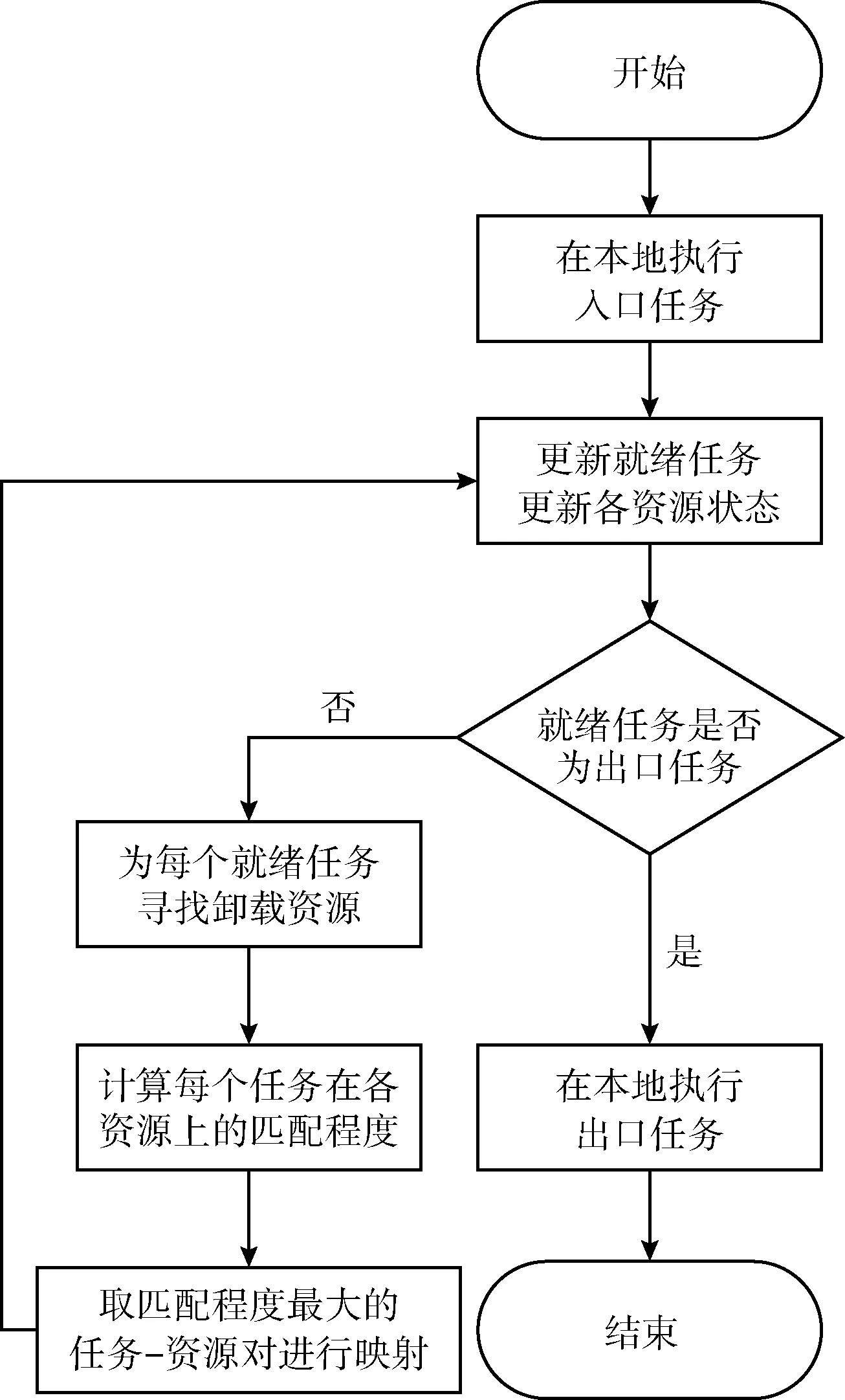
2.1 可用资源的选择
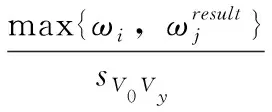

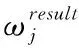

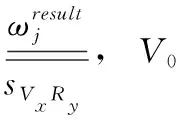

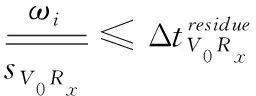
2.2 任务-资源映射

3 实验仿真
3.1 参数设置

3.2 实验设计与结果分析


4 结束语
