关于矩阵乘法问题的人工蜂群优化算法研究*
2021-12-23庄鹤林杨火根夏小云廖伟志
庄鹤林,杨火根,夏小云,廖伟志
(1.江西理工大学理学院,江西 赣州 341000;2.嘉兴学院信息科学与工程学院,浙江 嘉兴 314001)
1 引言
矩阵乘法是数值计算中的一个基本运算,在科学研究和工程分析中有着广泛的运用。矩阵乘法的计算时间直接影响了应用领域的时间复杂度。
1969年,德国数学家Strassen[1]提出了一个新的分治矩阵乘法算法,将矩阵乘法的时间复杂度从O(n3)降低至O(n2.81),大大提高了矩阵乘法的效率。
Strassen算法提出之后,众多数学家尝试寻找更好的算法。当前最好的矩阵乘法算法时间复杂度为O(n2.376)[2]。已经证明了当使用(n/2)×(n/2)矩阵的线性组合时,不可能使(n/2)×(n/2)矩阵乘法仅用6次乘法完成[3]。对于(n/3)×(n/3)矩阵,当前最好的算法需要至少23次乘法[4]。
快速矩阵乘法算法能够通过穷举所有可能的情况获得,然而计算量过于巨大,难以实现。近年来,研究人员提出使用计算机算法求解快速矩阵乘法,他们使用遗传算法找到了与Strassen算法等同时间复杂度的矩阵乘法算法。2001年由Kolen等人[5]提出使用进化算法推导Strassen算法,但其增加了过多的约束条件,效率非常低,并且只能找到与Strassen完全相同的算法。2010年,Oh等人[6]对遗传算法进行了改进,使用杂交和局部搜索方法,并使用高斯消除法和线性无关等计算适应度,效果有了明显改进,找到了大量不同于Strassen算法却与其有相同时间复杂度的算法,并对各个算法进行了分类比较和分析。但是,这些算法的求解效率仍不让人满意,平均计算时间需要几个小时。此外,Zhou等人[7]使用蚁群算法也重现了Strassen算法,找到了与Strassen算法同等时间复杂度的10种不同类型的解,求解时间相比遗传算法从数小时下降到数秒钟。最近,Heule等人[8]基于SAT的局部搜索算法,找到了仅使用23次乘法的(n/3)×(n/3)矩阵乘法的新模式。
群体智能优化算法源于对自然界的生物进化过程或觅食行为的模拟[9 -11],它将搜索和优化过程模拟成个体的进化或觅食过程,用搜索空间中的点模拟自然界中的个体,将求解问题的目标函数度量成个体对环境的适应能力,将个体的优胜劣汰过程或觅食过程类比为搜索和优化过程中用好的可行解取代较差可行解的迭代过程,是一种求解极值问题的自适应人工智能技术。
人工蜂群算法是一种模拟蜜蜂行为的优化算法[12 -14],该算法参数相对较少、易于实现,具有较快的收敛速度,且融入了反馈思想,跳出局部能力强,获得了众多学者的关注,其在TSP问题[15]、函数优化[16]和流水线调度[17]等优化问题中获得了广泛的应用。
本文将基于2×2快速矩阵乘法问题转换为一个组合优化问题,提出使用人工蜂群智能算法来求解该问题,结合问题本身特点对人工蜂群算法进行改进并用于矩阵乘法问题搜索求解。本文所提算法充分利用群体智能算法的固有并行性、鲁棒性和全局优化等特点,针对优化问题自身特点设计适应度函数,优化搜索空间,能进行有效的快速矩阵乘法算法搜索。
2 快速矩阵乘法问题描述
2.1 快速矩阵乘法问题
对于如式(1)所示的n×n矩阵乘法,
AB=C
(1)
需要构造一组Pi(i=1,2,…,m),可描述为如下形式:
aij,bij∈{-1,0,1}
(2)
当Cj(j=1,2,3,…,n2)都可由Pi(i=1,2,…,m)线性组合来表示以及m 目前已经证明2×2矩阵乘法至少需要7次乘法,即m最小取7。需要构造一组Pi(i=1,2,…,7),描述为如下形式: aij,bij∈{-1,0,1} (3) 当Cj(j=1,2,3,4)都可由Pi(i=1,2,…,7)线性组合来表示时,即找到2×2矩阵乘法的一个快速算法。 分析可得,每个Pi有8个变量,总共有7×8=56个变量。对于每个Pi,所有变量全0是无意义的,并且对于任意一组Pi,将任意一个或多个Pi的所有变量取相反数后逻辑上与原来的Pi组相同,即变化后的Pi组能线性表示的Cj,原Pi组也能线性表示。故对于任意Pi的(ai1ai2ai3ai4)和(bi1bi2bi3bi4)在赋值时能够按照排除全0、首个非0系数必须为1(或-1)的原则去掉无意义或逻辑重复的选择,剩余2×2快速矩阵乘法的系数选择共40个,记作choicei(1≤i≤40)。每个Pi有40×40=1600种赋值方法。这1 600种赋值方法记作combi(1≤i≤1600),即comb40(i-1)+j=(choicei,choicej)。 将问题用矩阵的形式描述,Pi(i=1,2,…,7)的全部系数记录在一个矩阵里,记作XS7×8,如下所示: XS7×8唯一决定一个Pi组对应的矩阵P16×7,P16×7的每一列(Pi)唯一对应一个Pi。P16×7如下: 其中,XS7×8的第i行对应P16×7的第i列,转换公式如式(4)所示: Pij=XSj,(i-1)mod 4+1×XSj,(i-1)mod 4 + 5 (4) C1=A1B1+A2B3, C2=A1B2+A2B4, C3=A3B1+A4B3, C4=A3B2+A4B4 (5) 给出Q16×4如下: Q16×4的第i列(Qi)与Ci唯一对应。 2×2矩阵乘法问题转化为寻找一个XS7×8,其对应的P16×7,存在一个矩阵H7×4,使P16×7H7×4=Q16×4成立。 在结果用矩阵表示的情况下,可用一个XS唯一表示一个解。下面给出将矩阵形式的结果转化为普通结果的公式。 (6) 对于成立的PH=Q,Ci的表达式如式(7)所示: (7) 其中,H需要通过广义逆计算,计算公式如式(8)所示: H=P (8) 其中,为广义逆中的左除运算。 描述1矩阵按列连接:对于2个行数相同的矩阵A和B,记A|B为A和B按列连接而成的增广矩阵。 描述2遍历操作:将XS第i行的赋值依次替换为comb1,comb2,…,comb[(3n2-1)/2]2,对每一个替换结果都访问一次的过程称为对XS第i行的遍历。对XS的遍历即为对XS的每一行都遍历一遍。对XS的第i行遍历在逻辑上等价于对P的第i列遍历和对Pi遍历。 描述3遍历位置(i,a,b):comb的每一行可由2个系数决定,记作a和b。a即该行中的(ai1ai2ai3…ain2)在choice中的序号,b即该行中的(bi1bi2bi3…bin2)在choice中的序号。当对某一XS的第i行进行遍历操作时,其遍历位置可由(i,a,b)唯一确定。 定义1(不同解) 对于2个XS,其中一个XS中存在一行向量在另一个XS无相同行向量,这2个XS即为不同解。 一组Pi即为一个解,而一个XS唯一决定一组Pi,因此用XS记录一个解。为在记录时避免逻辑上的重复记录,定义不同解,因为非不同解(相同解)在逻辑上是相同的。 定义2(相邻解) 对某一XS进行遍历操作时,找到的与原本XS适应度相同的所有XS都称为其相邻解。 定义3(邻位更优解) 对某一XS进行遍历操作时,找到的比原本XS适应度高的所有XS都称为其邻位更优解。 定义4(劣质解) 对某一解,若自身及其所有相邻解在遍历过程中都找不到邻位更优解,称该解为劣质解。 此外,本文中用到的矩阵的秩即为极大线性无关组所含向量的个数。 人工蜂群算法ABC(Artificial Bee Colony algorithm)是一个由蜂群行为启发的算法,于2005年由Karaboga[12]为优化函数问题而提出。 蜜蜂是一种群居昆虫,虽然单个昆虫的行为极其简单,但是由多个简单的个体所组成的群体却表现出极其复杂的行为。真实的蜜蜂种群能够在各种环境下,以极高的效率从食物源中采集花蜜。 人工蜂群算法的主要组成部分包括食物源、雇佣蜂和非雇佣蜂。人工蜂群算法的2种最基本的行为模式为蜜源招募蜜蜂和放弃某个蜜源。食物源的好坏对应于算法中的适应度。雇佣蜂对应一个食物源,并与其它蜜蜂分享此食物源信息,食物源越好招募到其它蜜蜂的概率越大。非雇佣蜂分为侦查蜂和跟随蜂,跟随蜂在食物源附近搜索新的潜在食物源,侦查蜂搜索新的食物源。 在初始化后,该算法的每次迭代主要分以下3个阶段。 (1)雇佣蜂阶段:一个雇佣蜂与一个食物源对应。雇佣蜂在邻域搜索并依据贪心算法更新。 (2)跟随蜂阶段:跟随蜂依概率选择雇佣蜂带回的食物源信息对应的食物源搜索邻域并依据贪心算法更新。 (3)侦查蜂阶段:当某个可能解迭代limit次仍没有改进时,就认为此食物源不好,此时对应雇佣蜂转化为侦查蜂,放弃该食物源,同时随机生成一个新的食物源。 雇佣蜂和跟随蜂在搜索邻域时,选择邻域的一个小区域遍历。多个跟随蜂选择同一蜜源搜索邻域时,极可能会出现重复搜索的情况。为避免此情况,本文基于基本ABC进行优化,对于一个蜜源,对其7个Pi遍历采用绕圈的方式搜索邻域,如图1所示。 Figure 1 Circle traversal图1 绕圈遍历 每个Pi初始起点分别为comb中随机的一个位置。无论是雇佣蜂还是跟随蜂,选中一个Pi遍历时,都从当前起点开始,顺序搜索一定范围的邻域,并用最后的位置更新起点。如果适应度改进,则再次随机初始化所有Pi的起点。这样,使随机性体现在Pi的选择和初始起点上。 一个花蜜由7个Pi组成,对其中某个Pi遍历时,在其它6个Pi不发生改变时,再对已遍历部分搜索是没有意义的。绕圈遍历的作用在于,当某一蜜源中的某一Pi被重复选中时,搜索会从新的起点开始,除非再绕了一圈,否则已搜索部分不会被重复搜索。 某解自身与其相邻解,若不进行完整遍历,不确定该解是否为劣质解。若非劣质解,也不确定哪一个或哪几个相邻解存在邻位更优解。各个Pi都在随机到来的绕圈中变化着。绕圈遍历作为邻域搜索策略,其目的在于保证解的适应度不降低,并且等待邻位更优解的出现。 向量组A可线性表示向量组B的充要条件为R(A)=R(A|B),其中R(A)为矩阵A的秩。一个矩阵即为一个向量组,根据该充要条件,向量组能否线性表示另一向量组可转化为对矩阵秩的判断。 判断是否所有Ci可由Pi组线性表示,即判断Pi组是否为可行解,只要判断P与P|C的秩是否相等即可。这在使用穷举法时是可行的,然而对于群体智能算法而言不能仅做此简单的判断。群体智能算法是一类在迭代过程中逐渐趋优的算法,对于解的好坏要有更准确的描述。 判断Ci是否可由Pi组线性表示,只要判断P与P|Ci的秩是否相等即可。当Pi组能够线性表示的Ci越多,认为其适应度越好。故判断适应度的好坏,需计算所有P|Ci中与P的秩相等的个数,再利用此数对适应度进行映射。适应度按照升序或降序的原则设置。 为更好地描述某一解的收敛情况,称可线性表示t个Ci的解收敛至第t级。特别地,当t=n2时,表示该解收敛至可行解。 本节给出用于2×2快速矩阵乘法的人工蜂群算法。作为随机启发式搜索算法,适应度的计算在算法搜索过程中起到关键的作用[18]。对于本文中的矩阵乘法问题而言,适应度的意义仅为区分解可线性表示的Ci的个数,故采用如式(9)所示的适应度计算公式: S=ne+1 (9) 其中,ne为该解对应的Pi组可线性表示的Ci的个数,最后一项加1是为了避免赌盘选择时总适应度为0导致计算时存在分母为0的情况。算法中使用的邻域搜索策略为从起点开始遍历,直到找到一个邻位更优解或向后400个comb。具体算法步骤如算法1所示: 算法1快速矩阵乘法的ABC算法 输入:无。 输出:可行解。 步骤1随机初始化蜜源Xi(i=1,2,…,SN)。 步骤2进入循环。 步骤3每个雇佣蜂对对应蜜源随机选择一个Pi按照绕圈遍历邻域搜索策略搜索邻域,用此邻域中适应度最高的解更新蜜源,若有多个,采用赌盘算法选择其中一个。若适应度改进,则再次初始化这个蜜源的所有起点,并再次初始化其limit。 步骤4每个侦查蜂按照赌盘算法选择一个蜜源,随机选择一个按照绕圈遍历邻域搜索策略搜索邻域。用此邻域中适应度最高的解更新蜜源,若有多个,采用赌盘算法选择其中一个。若适应度改进,则再次初始化这个蜜源的所有起点,并再次初始化其limit。 步骤5侦查蜂使每个蜜源limit减1,并丢弃所有limit为0的蜜源。随机生成蜜源至蜜源数为SN。 步骤6若找到可行解或运行时间达到上限,循环结束。 雇佣蜂阶段和跟随蜂阶段的操作基本一致,但二者的作用有所区别。每只雇佣蜂固定搜索自己对应的蜜源的邻域,以保证每轮迭代中每个蜜源有至少一次的邻域搜索。而跟随蜂则是让适应度更好的蜜源有更多邻域搜索的机会,以形成正反馈。 在2×2矩阵乘法中,一个解能够线性表示3个Ci,看似距离线性表示全部4个Ci仅一步之遥,而在实际算法运行中,收敛至第3级一般只需要几秒钟,而在此基础上收敛至第4级通常需要数分钟。 2.4节中给出了劣质解的概念,实验中发现,劣质解大量存在,是从第3级收敛至第4级困难的主要原因之一。 如果不采取有效的策略,那么程序就会在劣质解的邻域搜索上浪费大量的时间,降低了算法效率。然而事实上,许多算法的策略仅仅是设置一个迭代上限,若达到迭代上限则重新初始化,这并不能有效地减少程序在劣质解的邻域搜索。 人工蜂群算法融入了正反馈与负反馈的思想,这是它性能优秀的关键因素,这个特性非常适合于快速矩阵乘法问题求解。适应度高的蜜源会招来更多的侦查蜂搜索其邻域,而适应度低的蜜源一旦被判断不好,就会被丢弃。实验时将limit设置为30,当某一蜜源连续30代适应度都未提升时,抛弃该蜜源。对于某一解,其自身无法收敛至下一级,但是却无法确定其相邻解是否能收敛至下一级。当然,它可能是个劣质解,其所有相邻解都无法收敛至下一级,设定limit为30,能够避免浪费过多时间在劣质解的邻域搜索上,并且又不会太快地抛弃一个可能优质的解。 为探讨本文所提算法的性能,首先对其时间开销进行分析。算法大部分时间用于雇佣蜂阶段和侦查蜂阶段的邻域搜索,侦查蜂阶段相比之下可忽略不计。理论上其每一次迭代所用的平均时间与种群大小(SN)成正比。为验证此分析,在不同种群大小下分别进行5次重复实验,实验环境为同一计算机的相同运行环境,结果如表1所示。 Table 1 Running time of the 1 000 iterations for different population sizes 表1 不同种群大小SN下迭代1 000代所需的时间 s 分别在种群大小为7,10,15下进行采样,得到的平均时间与种群大小呈现一致比例。 此外,由于影响算法性能的参数较多,研究时仅凭经验将limit设置为30,将每次邻域搜索的最大范围设置为400个comb,使雇佣蜂和跟随蜂的数量相等,其数值就是种群大小。剩余影响算法效率的参数就是种群大小。 上面已经分析了每一代所需的时间可近似与种群大小成正比,那么仅需对不同种群大小下得到一个可行解所需的迭代次数进行实验便可分析其性能。对不同种群大小下找到一个可行解所需的迭代次数分别进行了30次独立实验,结果如图2所示。 Figure 2 Relationship between population size and iteration图2 种群大小与迭代次数关系图 种群大小为10和15时的迭代次数波动情况相近,而种群大小为7时的迭代次数波动范围大,且总体数值要高于总群大小为10和15时的。 每一代所需的时间可近似与种群大小成正比,那么将搜索到一个可行解所需的平均迭代次数G与种群大小乘积的倒数定义为效率E。分别取30次独立实验的迭代次数的中位数和平均数计算不同种群大小下的中位效率(Em)和平均效率(Ea)。计算结果如表2所示。 Table 2 Search efficiency for different population sizes表2 不同种群大小下的搜索效率 由于计算结果偏小,将结果做了乘以10 000的处理。可以看到,无论是从中位数还是平均数来看,种群大小并非越小越好,也非越大越好,事实上经测量,种群大小在小于7时,效率会急剧下降;在高于15时也会一直下降。实测得到在limit为30以及邻域搜索范围最大值为400comb时,种群大小设定为10左右效率是最高的。 为定量分析本文所述改进ABC—IABC (Improved Artificial Bee Colony algorithm)的性能,将其与基本ABC—BABC (Basic Artificial Bee Colony algorithm)、一种基于拥挤度概念的改进ABC—CABC (Artificial Bee Colony Algorithm based on Congestion concept)[19,20]以及其它一些算法进行对比实验。 目前已有许多算法用于搜索2×2快速矩阵乘法,本文选用这些算法中同为群体智能算法的遗传算法GA(Genetic Algorithm)[6]与非群体智能算法的随机搜索算法RS(Random Search)[21]作为代表进行对比实验。另外,粒子群优化算法与烟花算法在大量的研究中被证实具有较高的性能,本文选取它们的中值粒子群优化算法MPSO(Median-oriented Particle Swarm Optimization)[22]和自适应烟花算法AFWA(Adaptive FireWorks Algorithm)[23]进行对比实验。 7种算法的实现均在同一编程环境,除各自算法策略,其它部分使用相同的数据结构。在相同条件下,进行3次重复实验。每次重复实验运行11个单位时间,每隔1个单位时间采样记录一次当前搜索到的不同解的个数。取3次实验的平均值,结果如图3所示。 Figure 3 Solution numbers found by BABC,CABC,IABC,GA,RS,MPSO and AFWA in different running time图3 7种算法搜索不同解数量随时间变化图 从图3可以看出,3种ABC的性能都明显优于GA和RS的,2种优化ABC较BABC性能都有所提升;AFWA的性能接近BABC的,而MPSO的性能仅比RS的略高。 由于矩阵乘法问题解空间的复杂性,特别是劣质解的存在,使得GA的交叉操作和PSO的极值跟踪操作难以使解收敛,而ABC和AFWA基于反馈的邻域搜索机制能够有效地使解收敛。 对于一种搜索算法,评价其性能指标的重要因素包括搜索不同解的能力。如果在已搜索到的解的基础上难以再搜索到新解,即搜索到的都是重复的解,也是不合格的。从图3中可以看到,在已搜索到150个以上不同解的基础上,IABC搜索到的新解总数仍保持较高的增长速度,而CABC的搜索速度已明显下降,这也证实了IABC在搜索新解方面的优秀性能。 本文采用人工蜂群算法重现了Strassen快速矩阵乘法算法。由于快速矩阵乘法问题的自身特性,尤其是劣质解的存在,使得融入反馈思想的ABC相较其它经典算法有极大的优越性。本文在基本ABC的基础上,采用了绕圈遍历方法改进,避免了邻域的重复搜索。实验结果证实了人工蜂群算法的优越性,以及在此基础上绕圈遍历策略带来的性能提升。 关于快速矩阵乘法算法,当前对其解的适应度描述分为5个等级,即一个解可线性表示0,1,2,3,4个Ci映射的5个等级。算法中适应度的设置对算法的性能影响较大,尤其是对于大的搜索空间而言,仅用5个适应度划分等级是明显不够的。因此,寻求更优的适应度函数对于矩阵乘法问题尤为重要。 此外,3×3快速矩阵乘法算法[24]搜索空间相对于2×2快速矩阵乘法要大得多[4]。如何寻找更加高效的智能搜索算法进行快速矩阵乘法求解仍然是一个巨大的挑战。2.2 2×2快速矩阵乘法问题

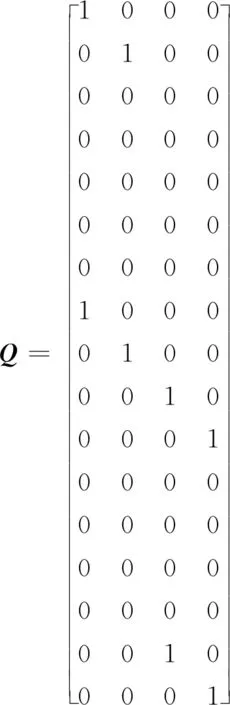
2.3 可行解结果转换
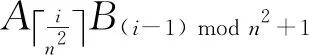
2.4 描述与定义补充
3 基于人工蜂群算法的2×2快速矩阵乘法算法
3.1 人工蜂群算法(ABC)
3.2 ABC算法优化

3.3 适应度设置与计算方法
3.4 2×2快速矩阵乘法的ABC算法
3.5 算法有效性分析
4 实验分析
4.1 优化ABC的时间开销与参数的关系
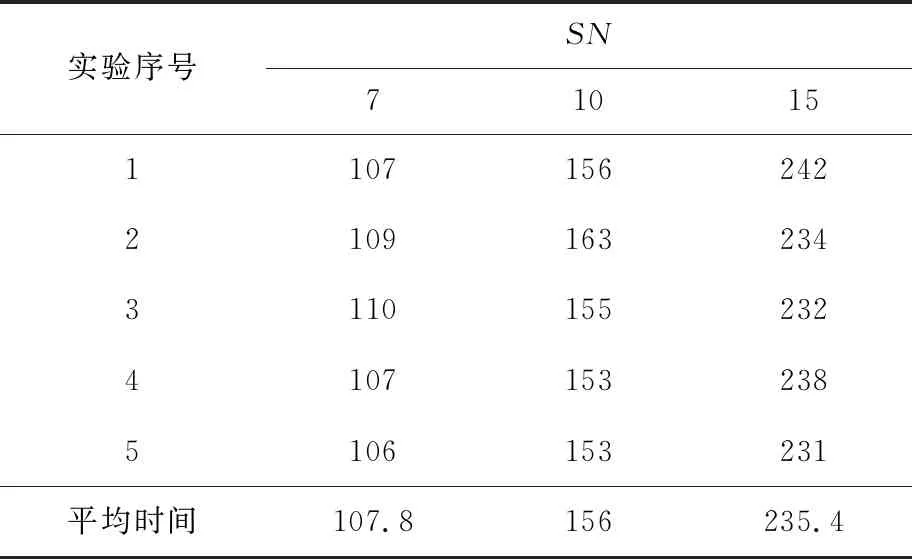


4.2 优化ABC与其他算法的性能比较

5 结束语
