MAPSAC与EKF结合的单目相机鲁棒定位估计算法与实验验证

孙 浩，冯孝周，张见升，王艳艳，高俊钗

(1.西安工业大学，陕西 西安 710065；2.中国兵器工业试验测试研究院，陕西 华阴 714200)

0 引 言

路标与图像中成像特征点的正确数据关联关系到单目相机定位估计的准确性，是单目相机定位方法的关键[1，2].由于单目相机获取环境信息的平滑性、重复纹理的存在以及图像处理引入的噪声等，已有的数据关联方法ICNN[3-5](Individual Compatibility Nearest Neighbour，ICNN)对环境路标和成像特征进行数据关联时会存在模糊关联的情况，即一个路标可能关联多个成像特征，或者一个成像特征可能与多个路标关联，从而引起错误的数据关联.对含有错误关联的数据直接采用最小二乘法或者卡尔曼滤波方法估计单目相机的定位，会导致定位估计的不准确性，所以定位估计时需要剔除错误关联的数据.RANSAC(RANdom SAmple Consensus，RANSAC)[6-8]是一种考虑了剔除错误数据关联的统计模型鲁棒估计方法，它采用随机抽样寻找最大一致集的方法剔除错误关联数据(外点)，并同时可以利用正确的关联数据(内点)对单目相机进行较准确的定位估计.但该方法有一个假设，即在所有的关联数据定位估计模型中，正确关联数据定位估计的是主要模型.在自然环境中，错误关联数据是随机的，其正确定位估计有时不会占主要模型，从而不满足这个假设.而且RANSAC数据关联方法对内点不再进行区分，使得单目相机定位估计的准确度受到影响，并且其定位模型估计样本需要的数据对较多，估计效率不高.

针对单目相机定位过程中，路标与图像中成像特征点的数据关联存在错误关联的问题，在ICNN数据关联基础上，提出了MAPSAC(Maximum A Posteriori SAmple Consensus，MAPSAC)[9]与EKF(Extended Kalman Filter，EKF)[10，11]结合的路标与图像中成像特征点错误关联数据剔除的单目相机定位鲁棒估计方法，给出的MAPSAC损失函数不仅可靠地剔除了错误关联的数据，而且对数据关联的内点进行了有效的区分；通过MAPSAC的最小化损失函数，可以实现单目相机定位的鲁棒估计，增强算法的环境适应性.结合单目相机状态的EKF更新方程，提高了数据关联的效率，通过仿真和实验分析，该方法可以实现相机鲁棒定位估计.

1 基于RANSAC的单目相机定位鲁棒估计分析

根据RANSAC单目相机定位鲁棒估计算法的原理，对其选择正确样本的计算复杂度较高以及损失函数对内点不做区分的问题进行了分析.

1.1 基于RANSAC的单目相机定位鲁棒估计原理

在单目相机EKF 定位过程中，RANSAC的数据关联算法通过反复选择路标与成像特征点数据中的一组随机样本，得到主要的单目相机定位模型.首先，随机选取最小的一个样本假设为单目相机定位模型的内点集，基于直接线性方法确定单目相机定位模型；然后对其它关联数据用得到的单目相机定位模型去检验决策，如果符合估计的单目相机定位模型或具有较小的距离误差，则判断为该定位模型一致集的内点，并用所有一致集的内点进行单目相机定位模型估计.如果内点越多，估计的单目相机定位模型就越稳定；最后根据设定的迭代次数重复执行上述过程，统计单目相机定位模型所含的内点数量对定位模型进行选择，舍弃内点太少的单目相机定位模型，得到含有最大一致集内点的单目相机定位模型.

1.2 RANSAC的定位估计样本选择分析

对于单目相机定位算法中路标与成像特征点关联的数据，由于单目相机的射影成像，三维路标-二维特征成像点数据关联满足单目的射影成像关系，成像关系的内参数是不变的，单目相机定位外参数自由度为6，包含3个平移和3个旋转参数.由PnP[12，13]的n点定位原理可知：至少需要6对正确的数据关联点作为一个样本，可唯一地确定单目相机定位模型.为了估计的方便性，可以直接建立定位矩阵模型是3×4的矩阵，而不再需要估计具体的外参数.一个样本至少需要 6对点可唯一确定定位矩阵模型.

当路标与特征点关联存在错误关联时，在内点比例一定的情况下，获取一个定位矩阵模型估计的正确观测样本概率与观测样本的大小是非线性关系.假设路标与特征点关联的内点比例w=0.45，获取一个好的路标与特征点关联的观测样本的概率z=0.98的情况下，当观测样本大小为n时，抽样到一个正确的路标与特征点关联的观测样本所需的次数[14]

(1)

由式(1)可知，当观测样本J所需路标与特征点数据关联个数n增多时，抽到一个正确的路标与特征点关联的观测样本的次数K急剧增加，它们之间具体的对应数值如表 1 所示.

从表 1 可以看出，6对路标与特征点作为一个样本抽样到一个好观测样本的次数约是1对点时的78倍.所以，需要减少抽样次数，提高获得一个好观测样本的效率，从而加快数据关联的效率.

表 1 样本大小与抽样正确样本次数的关系

1.3 RANSAC的损失函数分析

设测量误差为ei；测量标准差为σ；被接受为内点的距离阈值为T，RANSAC算法的最大一致集实际上是对式(2)损失函数[15]的最小化

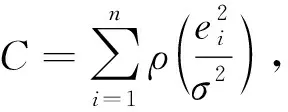
(2)

式中：

(3)

RANSAC算法距离阈值T的确定可以根据测量误差的先验分布或者根据先验经验选取，所以，RANSAC算法的一个不足之处是损失函数中对路标与特征点数据关联内点的处理方法，如果距离阈值T设置太高，此时内点之间将没有什么区别，而对外点的惩罚是一个常数，从而射影成像关联矩阵模型估计的性能将会变差[16].因此，距离阈值T越高，有相同C的估计性能越差.例如，若T足够大，则损失将会相同，因为每个数据关联对都将是内点，所以RANSAC的一个主要缺点是由于对路标与特征点数据关联的内点成因不明地用了均匀分布建模，所以对合适的距离阈值有较高的要求.而合适距离阈值的选取是一个比较困难的问题，所以为了降低距离阈值选择的难度，需要对内点集进行评价使用，有效提高定位估计的准确性.同时在自然环境中，错误关联数据是随机的，其正确定位估计有时不会占主要模型，RANSAC数据关联确定的最大一致集确定的参数模型可能不是正确的相机定位.

2 MAPSAC与EKF结合的单目相机定位鲁棒估计算法设计

针对RANSAC单目相机定位鲁棒估计算法的计算复杂度高、损失函数中距离阈值T确定以及环境适应性等问题，结合EKF更新选择单目相机的初始定位，提高了选择正确初始定位的概率，降低了计算复杂度.给出的MAPSAC损失函数确定定位估计的最小损失一致集，有效地衡量了内点定位的质量[17，18].

2.1 基于EKF更新的单目相机的初始定位估计模型

RANSAC在选用样本进行射影成像的初始定位估计时，参数估计的一个样本需要6对关联数据，得到一个正确样本所需的抽样次数较高.为了降低该抽样次数，结合单目相机的运动方程进行更新，采用一对关联数据的EKF更新确定初始定位，一对关联数据是指样本中s=1，就可以实现定位模型的拟合，大大降低了正确定位模型的抽样次数.该算法充分利用了EKF更新阶段得到的单目相机的定位状态，从路标与成像特征中选取1对关联数据，即可确定单目相机的初始定位模型[19].

假设经过数据匹配的路标集为Mi，相应的特征测量数据集为zIC={z1，z2，…，zi,……,zn}，组成的关联数据集为X={M，zIC}.在单目相机定位过程中，根据惯导测量相机的状态，设其运动方程[10]为

rk=f(rk-1，uk-1)+wk-1.

(4)

单目相机测量方程为

(5)

(6)

2.2 基于MAPSAC损失函数最小化一致集

在得到射影成像的初始定位估计模型后，就可以按照此模型确定其一致集.当关联数据与此模型的距离误差小于距离阈值时，则关联数据为该定位估计模型的内点集zinliers，否则为外点集.

针对RANSAC算法对内点不做区分，距离阈值根据先验知识确定的问题，结合后验概率模型，Torr等人随后提出了MAPSAC模型估计算法[9]，该算法使用最大化后验对数确定距离阈值

(7)

式中：ξ为内点的先验期望；σ为测量数据的标准差；ν为测量数据有界区域的体积；D为测量数据的维数；d为定位模型的维数.

在单目相机定位估计中，在给定定位估计模型参数Θ的情况下，对数据关联测量坐标分量X边缘化的同时，优化对内点与外点距离阈值Tmap的选择，可以通过式(8)最小化来完成

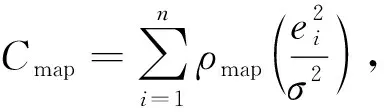
(8)

式中：

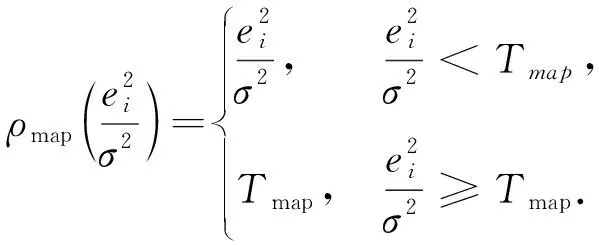
(9)

从式(9)可以看出，每个外点的损失函数相同，而对内点却根据他们拟合模型的好坏程度加以区别评价，这样降低了选择距离阈值的准确性，并且不会增加额外的计算.

2.3 MAPSAC与EKF结合的鲁棒定位估计算法

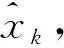
2) 从关联数据点集X中随机地抽取一对相容性关联数据J，根据式(6)的EKF更新估计初始定位参数ΘJ；

3) 选择与定位参数ΘJ几何距离小于距离阈值Tmap的相容性关联数据，用S(ΘJ)表示，为该定位参数ΘJ的一致集；

4) 当定位参数一致集S(ΘJ)中关联数据的数量#S(ΘJ)大于数量阈值th2时，根据式(5)，用一致集进行EKF更新，得到定位参数ΘJ，并输出关联数据一致集及相应的定位参数；当S(ΘJ)中关联数据的数量小于数量阈值th2，回到 2)；

通过以上步骤，则得到了一个最大一致集，即是单目相机定位估计所需要的正确的数据关联对，其它的相容性对应点都是外点集.滤除了误关联数据，同时获得了单目相机的定位估计.

3 数值仿真结果与分析

为了对提出的MAPSAC数据关联算法进行有效性的验证，采用直观的曲线模型拟合进行仿真验证.46个真实二维点分布如图 1 所示.

图 1 模拟曲线的二维数据

以图 1 的点作为真实点，并给每个真实点增加2个模拟测量数据，总共构成92个均值为[0,0]的模拟测量数据，并产生20个均值为[2,2]的高斯分布噪声，它们的协方差分别为

(10)

20个高斯分布噪声数据作为错误数据，用实心圆表示，如图 2 所示.

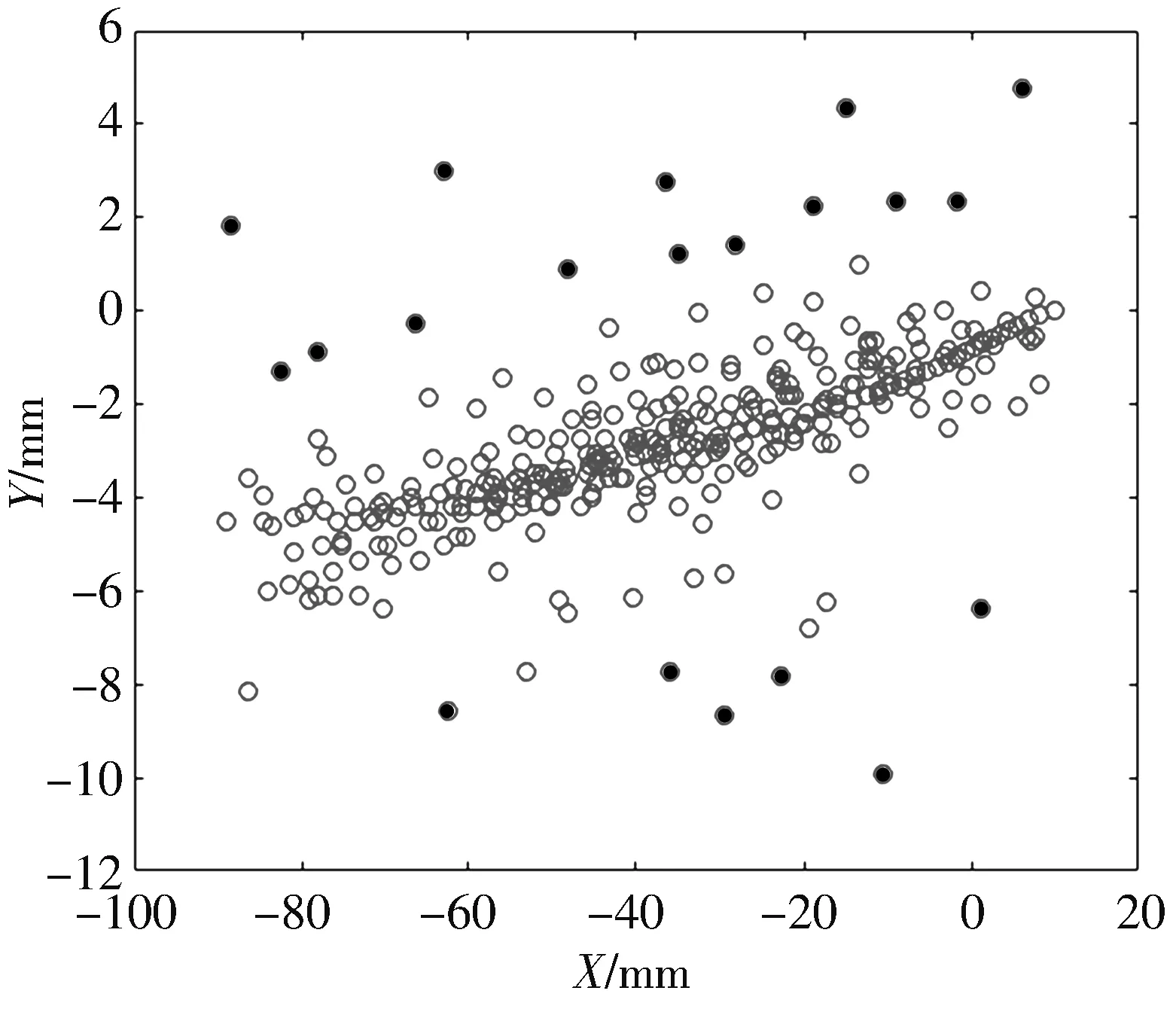
图 2 误差数据和错误数据分布

采用RANSAC进行数据关联，设置最大迭代次数为100，通过迭代，找到符合拟合模型的内点数据，如图3(a)所示的“⊕”，叠加在原始数据上.同样条件下采用MAPSAC进行数据关联，通过迭代，找到符合拟合模型的内点数据，如图 3(b)所示的“⊕”，叠加在原始数据上.数据关联过程中拟合曲线数据对比如表 2 所示.

通过图 3 可知，RANSAC与MAPSAC数据关联方法找到的关联数据相近，都比较正确地找出了散点的聚集函数，说明两种方法数据关联结果差别很小，都是有效的数据关联方法.

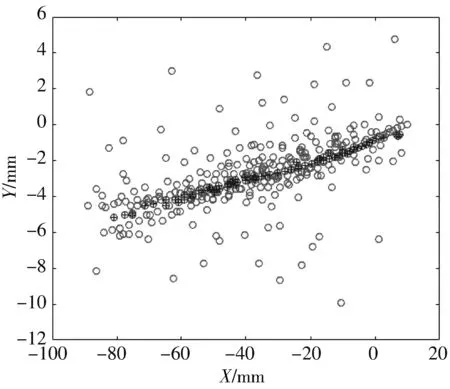
(a) RANSAC数据关联的内点结果

通过表 2 RANSAC与MAPSAC拟合曲线数据对比可知，两种方法找到的数据关联点有一点儿区别，拟合的曲线方程很相近，但MAPSAC的拟合误差比RANSAC小很多，说明MAPSAC数据关联模型估计方法的准确性.

表 2 RANSAC与MAPSAC拟合曲线数据

4 实验验证及精度分析

通过算法研究，利用该算法编制了专用数据处理软件，并结合相关实验进行了测量精度的对比验证.实验中采用3块木板搭建模拟飞散破片场的穿孔位置和大小，在地面用标志点模拟被试品所在位置及其方向，现场布置如图 4 所示.

图 4 试验现场布置

利用相机在不同位置进行成像，获取具有重叠区域的序列图像，采用本文所设计的算法，对相机成像时的位姿进行定位估计，结合匹配的破片穿孔位置进行三维重建，测量计算模拟破片穿孔位置.经过破片穿孔位置计算软件模块处理与计算，得到的模拟破片穿孔位置坐标如表 3 所示，并与用精度为0.03 mm的扫描仪得到的模拟破片穿孔位置坐标进行对比.

模拟破片穿孔数量为20个，通过表 3 可以看出，检测出模拟破片穿孔数量20个，破片穿孔坐标误差最大为0.86 mm，满足单个破片穿孔位置测量精度，说明设计的相机定位算法精度较高.通过实验验证，系统测量精度满足项目的技术指标要求.

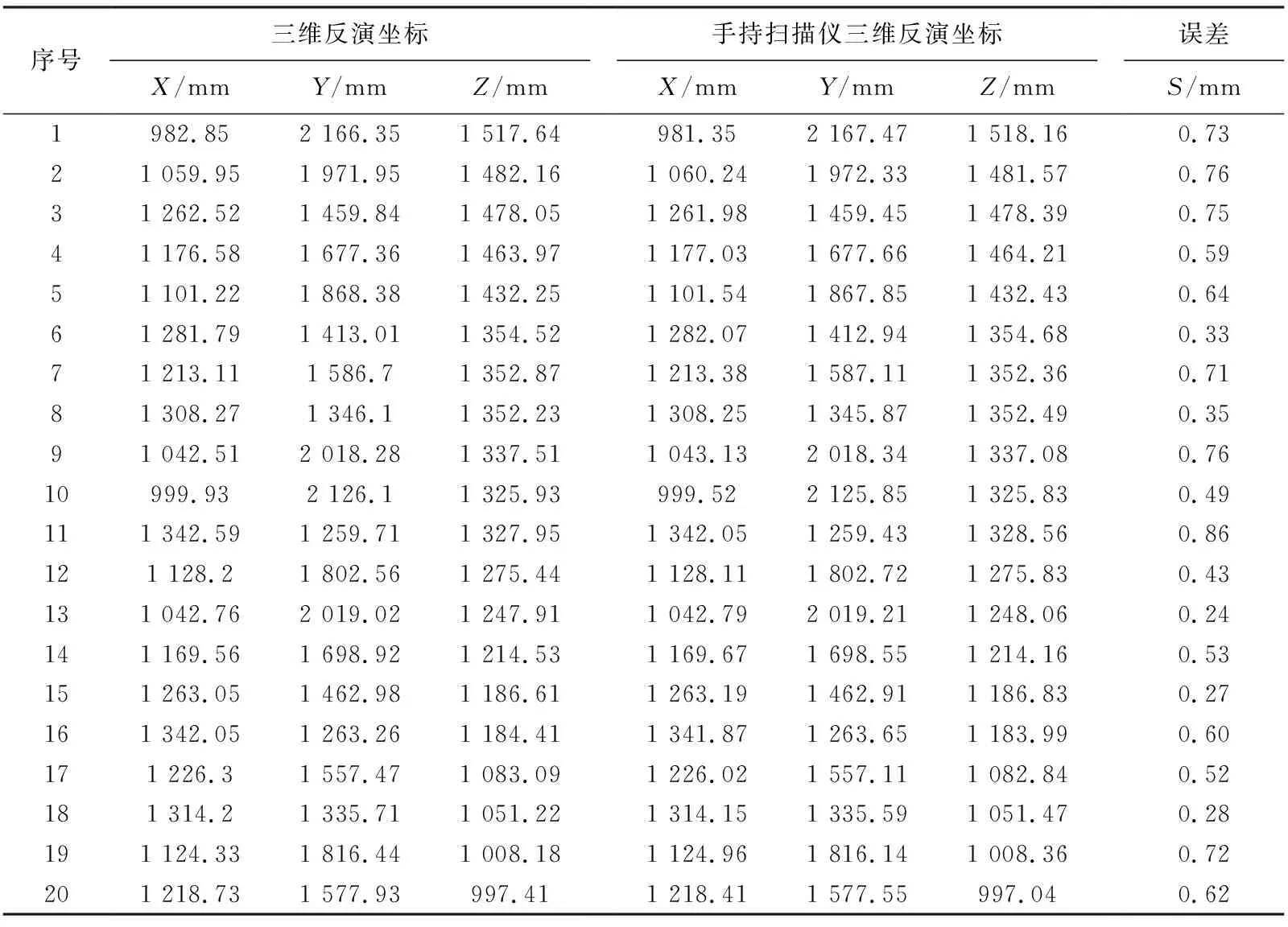
表 3 模拟破片穿孔坐标

5 结 论

本文针对单目相机定位中的含错误数据关联的定位估计问题进行了研究.在含有错误数据关联的情况下，结合单目相机运动方程的预测和更新，提出了MAPSAC与EKF结合的鲁棒定位估计算法，提高了定位估计的效率，给出了MAPSAC损失函数，有效提高了定位模型估计的准确性以及环境适应性.通过曲线模型数据关联仿真，说明所设计的定位估计算法可靠的抑制了噪声数据的影响，为单目相机定位估计提供了可靠的保障.结合该算法，编制了相关应用软件，在室外构建了模拟对象，对基于该算法的定位测量精度进行了对比验证，取得了良好的测试效果.后期将结合具体的项目需求，对算法模型和开发软件的实用性进行不断改进，进一步提高测试精度，并加强该技术的推广应用.