无人机系统中基于能量效率的资源分配研究
2021-12-23张志才尹振华
张志才,付 芳,尹振华
(山西大学 物理电子工程学院,山西 太原 030006)
0 引 言
无人机被认为是5G网络重要的组成部分,能为地面用户提供丰富的服务,如军事侦察、监控和公共安全等[1-3],目前学术界关于无人机通信系统的研究已经有了一定研究基础[4,5].文献[4]针对无人机系统的缓存放置问题,通过联合优化无人机路径和缓存内容放置以达到最大化吞吐量.文献[5]提出一种无人机路径规划模式,以保证信道吞吐量.需要注意的是,上述研究[4,5]都忽略了信息安全,然而,由于无人机通信信道的广播特性及信息传输的隐私性,无人机系统安全传输是不得不考虑的问题.虽然传统的应用层加密算法能有效地保证信息安全传输,但是这类方法的复杂度过高.近年来,物理层安全作为一种保密通信的技术手段受到学术界的广泛研究[6-10].文献[6]针对准静态衰落信道下无线通信网络场景,通过分析衰落信道的信噪比对保密速率和通信中断概率的影响,从而提出基于低密度奇偶校验码(LDPC)的密钥协议;文献[7]对无人机路径和时间调度进行了联合优化,实现了最小平均保密速率的最大化;文献[8]综合考虑优化无人机路径和功率控制,以最大化无人机通信系统下行链路的平均保密速率;文献[9]针对监控无人机下行传输场景,通过优化无人机路径以最大化接收端信干噪比,用凸优化理论求解.文献[10]综合考虑无人机路径规划和传输速率分配,以最小化无人机信息传输时的中断概率.需要注意的是,目前关于无人机安全通信的研究多以保密速率最大化[7,8]、或接收端信干噪比最大化[9]或中断概率最小化[10]为优化目标,没有考虑无人机飞行能量消耗的限制,然而,由于无人机电池容量有限,如何提高无人机的能量效率是非常重要的问题.本文旨在通过物理层安全容量描述数据传输速率定义能量效率并通过合理的功率控制使能量效率最大化,将此优化问题建模为MDP,用深度 Q 学习网络(DQN)来寻求最佳功率策略,在保证信息安全的同时合理分配功率.
1 系统架构
1.1 信道模型
如图 1 所示,本文设计了一种无人机信息传输和防窃取系统.该系统主要由软件定义网络(SDN)控制器、无人机(UAV)、地面宏基站(MBS)和多个窃听者(Eves)组成.无人机飞行在一个小区上空以广播的形式向MBS发送信息,窃听者随机分布在该小区里想要截获无人机发送的信息.假设无人机能通过机载摄像头或雷达探测到窃听者的位置,从而计算出无人机到窃听者之间的距离.为了掩藏和保护UAV发送的信号不被地面Eves非法窃取,MBS发射人工噪声干扰Eves,而MBS则可通过消除自身产生的干扰安全获取信息,即无人机和MBS之间的合法信道能够消除人工噪声的影响,但是无人机和窃听者之间的窃听信道由于不易消除人工噪声的影响而信道质量明显下降,从而保护无人机发出的信息安全传输避免窃听.SDN控制层中的UAV和MBS根据基础层获取的信道条件(CSI)等信息,通过控制UAV发射信号功率和MBS发射人工噪声功率以最大化能量效率和保证信息安全传输.
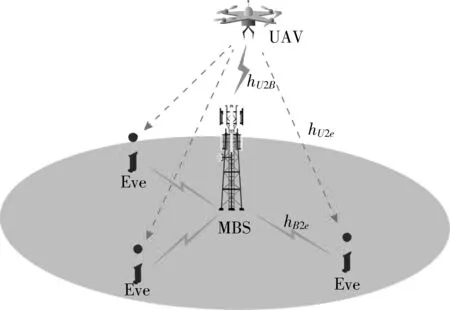
图1 网络架构图
为了表示方便,令UAV,MBS以及Eves 的位置在笛卡尔坐标系中分别表示为(xU,yU,zU),(xB,yB,0)和(xe,ye,0),e∈ε={1,2,3,…,E}表示窃听设备集合.因此,UAV与MBS之间的距离
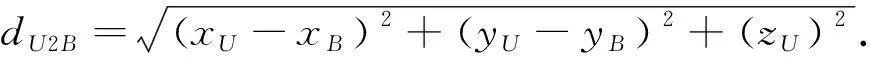
(1)
编号为e的窃听者记作Evee,UAV与Evee之间的距离

e∈ε.
(2)
MBS与Evee之间的距离
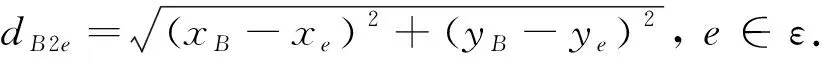
(3)
令hU2B表示 UAV与MBS之间的合法信道增益,hU2e表示UAV与Evee之间的窃听信道增益,假设它们均是由视距(LoS)主导的信道模型,则
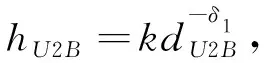
(4)
式中:dU2B表示UAV与MBS之间的3D距离,k为dU2B等于1 m时的单位信道增益,δ1为LoS信道的路径损耗指数.同理,hU2e满足
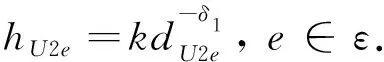
(5)
令hB2e表示MBS 与Evee之间的非视距(NLoS)信道增益,主要由大规模路径损耗和小型瑞丽衰落引起.则

(6)
式中:δ2为大规模路径损耗指数;ξ为小型衰落引起的遵循指数分布的随机变量.
1.2 安全传输能效模型
由于UAV的电池容量是一定的,如果用于通信设备的能量消耗过大,无人机的续航能力将会减小,并可能影响整个UAV系统网络.因此,本文在考虑信息安全的同时,将提高能量效率考虑在内.
传输速率是反映信息传输快慢的指标,根据香农公式,UAV与MBS之间合法信道的传输速率

(7)
式中:B表示带宽资源;pU(t)是无人机的发射功率;hU2B为合法信道增益;NB0是MBS的自然噪声功率.由于Eves在接收UAV信息的同时,也会受到来自MBS人工噪声的干扰,因此,窃听信道的传输速率
rU2E(pU(t),pB(t))=

(8)
式中:NE0表示窃听设备的自然噪声功率;pB(t)表示MBS产生的人工噪声功率.UAV与MBS之间的物理层安全容量可以定义为合法信道与窃听信道的速率差,即安全速率
r(pU(t),pB(t))=

(9)
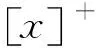
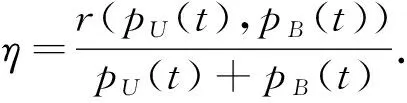
(10)
1.3 优化目标
本文通过SDN控制无人机发射有用信号的功率pU(t)和基站MBS发射人工噪声的功率pB(t),以实现在最大化能量效率的同时保证安全速率.无人机系统中的能效问题可表述为
Maximize∶η
s.t.minpU≤pU(t)≤maxpU,
minpB≤pB(t)≤maxpB,
(11)
式中:minpU与maxpU分别表示UAV的最小和最大发射功率;minpB与maxpB分别表示MBS的最小和最大干扰功率.约束条件的含义是,无人机发射有用信号的功率范围在minpU与maxpU之间,并且基站MBS发射人工噪声的功率pB(t)范围在minpB与maxpB之间.
1.4 问题建模与求解思路
对上述优化问题进行建模,考虑到无线环境的动态特性具有马尔科夫性质,因此我们将其建模为MDP〈S,A,P,r)〉,其中S表示状态空间,包括以下内容:
•UAV与MBS之间的距离dU2B;
•UAV与Eve e之间的距离dU2e,e∈ε;
•MBS与Eve e之间的距离dB2e,e∈ε;
A表示动作空间,包括以下内容:
•UAV发射有用信号的功率pU(t);
•MBS发射人工噪声的功率pB(t);
P∶S×A×S→[0,∞) 表示状态转移函数,由于很难精准预测状态转移函数,故采用无模型的深度强化学习算法来求解上述MDP问题;
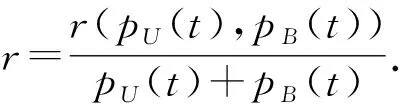
考虑到实际无人机网络环境动作和状态空间的连续性和多维度,以及相邻时隙动作的耦合性,传统以最大化短期回报为目标的优化方法很难保证长期回报最大化,而且由于Q学习过于依赖Q表,当动作和状态空间维度显著增加时,Q学习会发生维度灾难.策略梯度Policy Graident算法是基于策略搜索的强化学习算法,当无人机网络动态变化时,梯度易出现不稳定,导致收敛性能不好.针对无人机网络环境动作和状态空间具有多维连续的特征,采用DQN算法来求解上述MDP问题,它是一种基于值函数的深度强化学习算法,在训练时采用了Q学习的思路,用神经网络拟合Q学习中的误差项.
2 基于Deep Q-learning Network算法的资源优化
DQN算法采用神经网络近似值函数,如图 2 所示.算法包含两个结构相同参数不同的Q网络,分别为current Q网络和target Q网络.一个step中,agent在状态s下根据ε-greedy策略(π)做出动作a时会获得回报r,同时转移到下一状态s′,这些信息(s,a,r,s′)存储在Replay Buffer中,算法从中随机选取minibatch经验用于训练,从而打乱了相关性,使学习更有效率.由于动作a同时影响当前回报和未来收益,因此基于Bellman方程,current Q的近似值
Qπ(s,a)≈Q(s,a;θ)=r+γQ(s′,a′;θ),
(12)
式中:γ=[0,1]为折扣因子,θ为current Q网络的参数,该网络每隔N步将参数传递给target网络.current Q值Q(s,a;θ)与target Q值Q*(s,a;θ*)之差构成损失函数,即

(13)
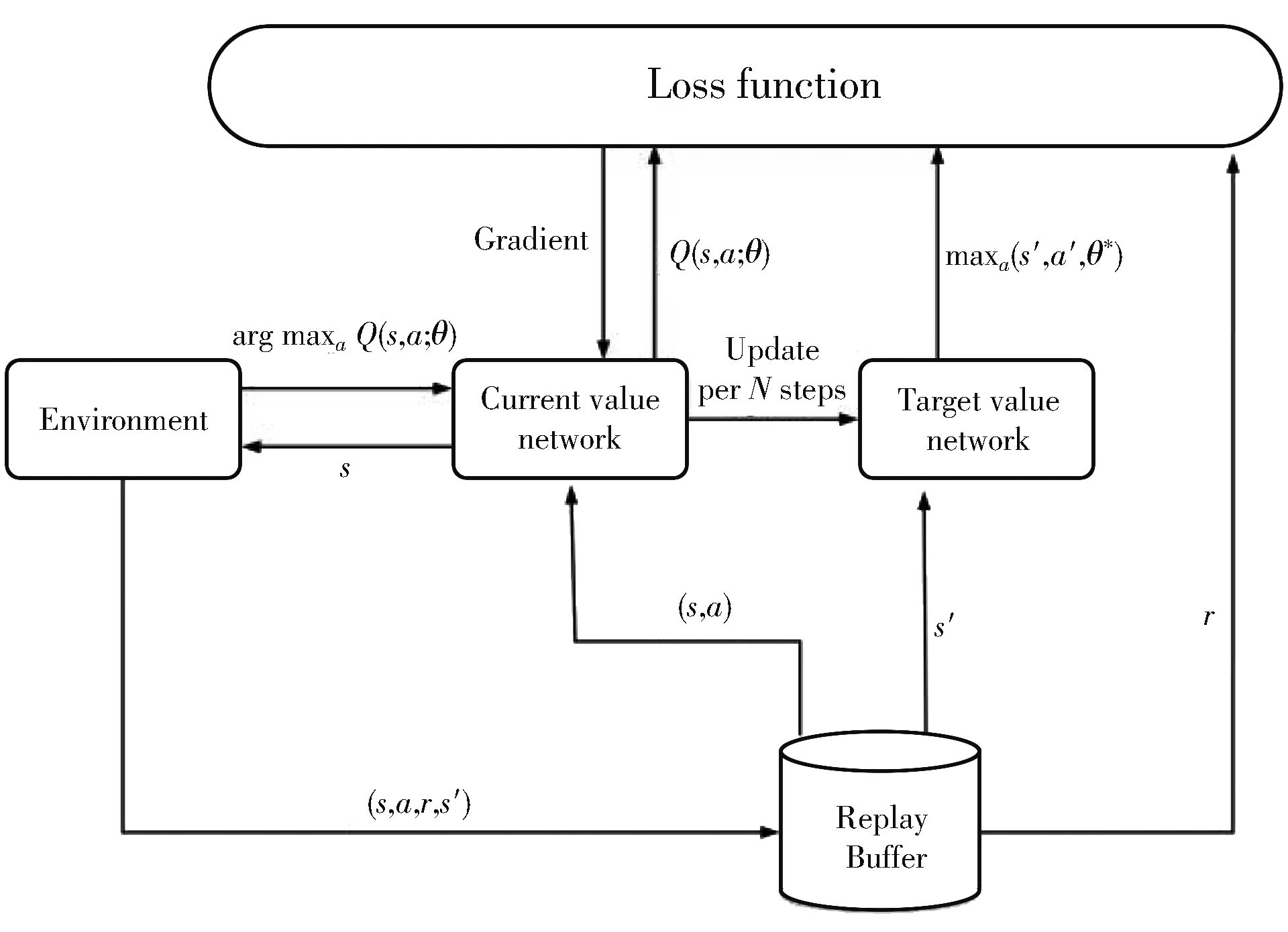
图 2 算法流程图
参数θ的更新公式为梯度下降
θi+1=θi+α∇θL(θ),
(14)
式中:0<α≤1为学习效率.
3 算法仿真与数据分析
本节中,针对本文提出的基于DQN算法的功率控制策略,在Python平台进行仿真.在覆盖半径为100 m的区域中,每个Episode随机初始UAV和MBS的位置,多个Eves的位置在每个Step均进行初始化,具体仿真参数如表 1 所示.

表 1 仿真参数设置
图 3 是DQN算法不同学习效率(α)的收敛图,从图 3 中可知,当α=0.1时,大约40个Episodes(每个Episode包含100个Step)可以收敛,而α=0.01时,大约需要300个Episodes才可以收敛,可见,在一定范围内,收敛速度会随着学习率的增高而加快.但并非学习率越高越好,如图 3 中,当α=0.5时,虽然收敛速度与α=0.1相当,但是收敛值明显更低,这是因为陷入了局部收敛.因此,最佳的学习率为α=0.1.

图 3 不同学习率收敛图
从图 4 可以看到,经典的Policy Gradient算法在400个Episodes左右可以达到收敛,收敛值大约比DQN算法低100,这是因为DQN中采用了ε-greedy策略,从而使探索更充分,避免陷入局部最优.因此,本文所提出的算法在回报值和学习速度方面都优于Policy Gradient算法,并且远胜过随机选动作的情况,可以说明本文算法的有效性.
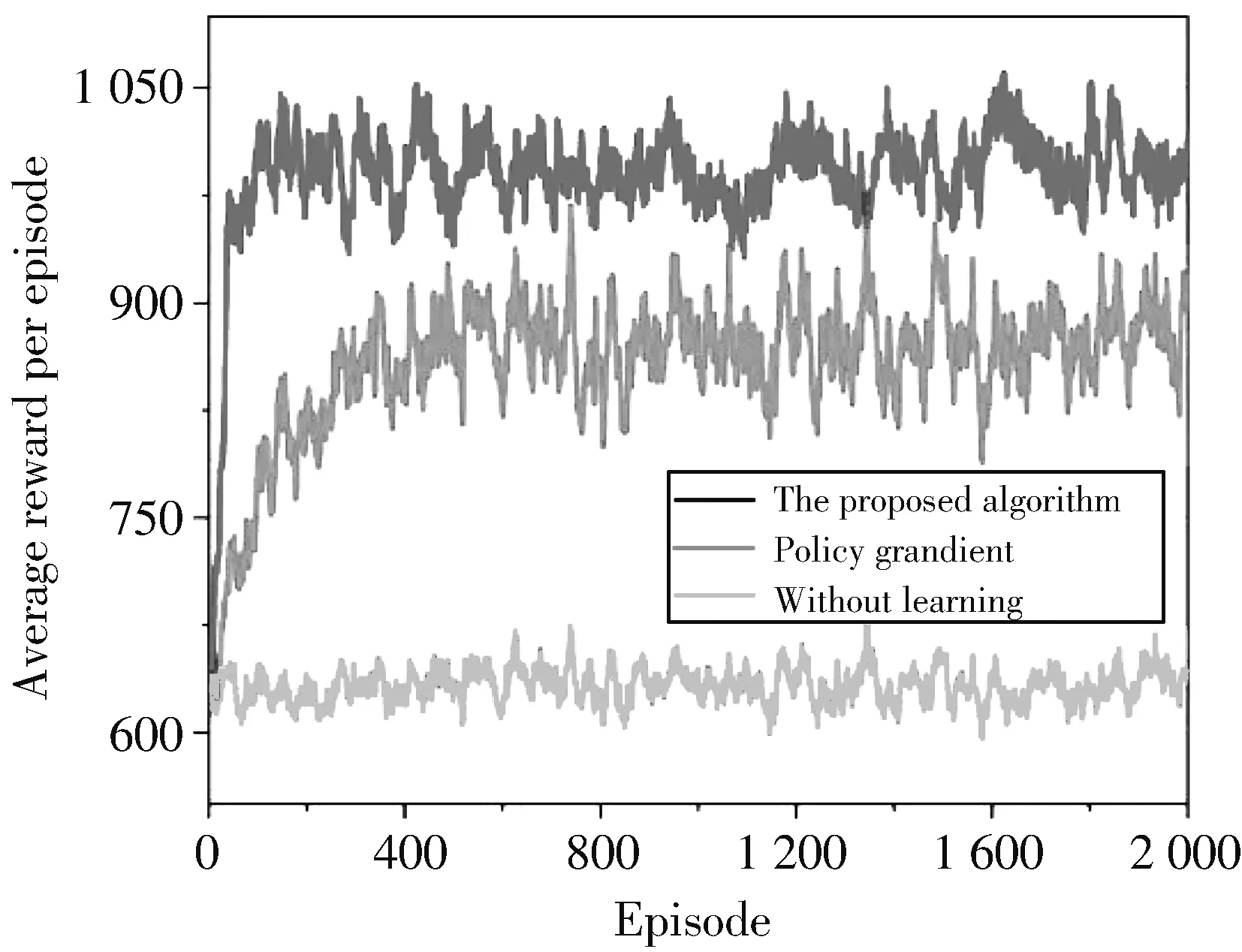
图 4 本文算法与其他算法的性能比较
图5为窃听者密度与平均回报之间的关系图,将UAV和MBS固定在半径为100 m的区域中随机撒点,变化Eves的密度和范围.可以看到,当覆盖半径一定时,随着窃听数量的减少,平均回报值会增大.当窃听数量固定时,随着覆盖半径的扩展,平均回报值逐渐增大.可见,区域面积窃听密度越小,平均回报值越高.
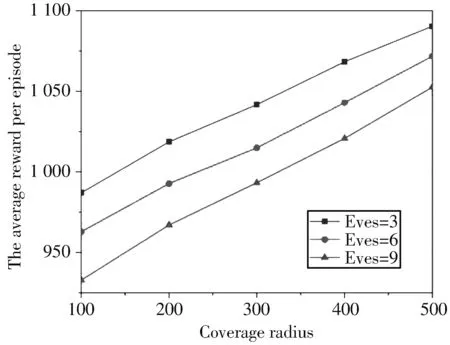
图 5 窃听密度与平均回报关系图
4 结 论
本文考虑了无人机系统中的物理层安全传输,主要研究了通过控制无人机发射有用信号的功率和MBS发射人工噪声的功率,在保证无人机信息安全传输的同时,最大化其能量效率.考虑到实际无人机网络环境动作和状态空间具有多维连续的特征,将上述优化问题建模为MDP,并采用DQN算法来求解最优功率控制策略.
